第十三届蓝桥杯国赛 C++ C 组 Java A 组 C 组 Python C 组 E 题——斐波那契数组(三语言代码AC)
目录
- 1.斐波那契数组
- 1.题目描述
- 2.输入格式
- 3.输出格式
- 4.样例输入
- 5.样例输出
- 6.数据范围
- 7.原题链接
- 2.解题思路
- 3.Ac_code
- 1.Java
- 2.C++
- 3.Python
1.斐波那契数组
1.题目描述
如果数组 A=(a0,a1,⋯.an−1)A=(a_0,a_1,⋯.a_{n-1})A=(a0,a1,⋯.an−1)满足以下条件, 就说它是一个斐波那契数组:
- n≥2;n≥2;n≥2;
- a0=a1a_0=a_1a0=a1
- 对于所有的 i(i≥2),i(i≥2),i(i≥2),都满足 ai=ai−1+ai−2。a_i=a_{i-1}+a_{i-2}。ai=ai−1+ai−2。
现在, 给出一个数组 AAA, 你可以执行任意次修改, 每次修改将数组中的某 个位置的元素修改为一个大于 0 的整数。请问最少修改几个元素之后, 数组 AAA 会变成一个斐波那契数组。
2.输入格式
输入的第一行包含一个整数 nnn,表示数组 AAA 中的元素个数。
第二行包含 nnn 个整数 a0,a1,⋯.an−1,a_0,a_1,⋯.a_{n-1},a0,a1,⋯.an−1,相邻两个整数之间用一个空格分隔。
3.输出格式
输出一行包含一个整数表示最少需要修改数组 AAA 中的几个元素之后, 数组 AAA 可以变为一个斐波那契数组。
4.样例输入
5
1 2 2 4 8
5.样例输出
3
6.数据范围
2≤n≤105,1≤ai≤106。2≤n≤10^5,1≤a_i≤10^6。2≤n≤105,1≤ai≤106。
7.原题链接
斐波那契数组
2.解题思路
首先考虑斐波那契数组具有什么性质,我们令 a0=a1=1a_0=a_1=1a0=a1=1去打印出前30位斐波那契数。
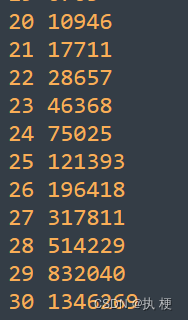
不难发现,在不到30位的情况下,斐波那契数组的值已经超出了1e6,而注意到题目给定的 aia_iai 的最大值才为 1e6。这说明其实后面的数我们根本无需考虑,都是必须要修改的。
接下来我们就只需要考虑前30位数最多可以保留多少个数,假设最多可以保留x个数,那么答案就为n-x。
对于斐波那契数列,如果 a0a_0a0 确定了,那么整个数列都确定了。所以我们可以枚举 a0a_0a0 的值,枚举的范围为[1,106]。[1,10^6]。[1,106]。然后去计算出前三十位的值,看与原数组符合预期的数有多少个,所有符合预期的数量取一个最大值x,最终答案即为n-x。
时间复杂度O(30∗106)O(30*10^6)O(30∗106)
3.Ac_code
1.Java
import java.io.*;
import java.util.Scanner;public class Main {static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int[] arr = new int[50];static int V = 1000000;public static void main(String[] args) throws IOException {Scanner sc = new Scanner(System.in);//表示无穷大int res = 0x3f3f3f3f;int n = sc.nextInt();int count = n;//我只读入前三十个数if (n > 30) n = 30;for (int i = 1; i <= n; i++) {arr[i] = sc.nextInt();}//枚举开头是多少 30*1e6 3e7for (int i = 1; i <= V; ++i) {int a = i, b = i, c = 0;int ans = 0;if (arr[1] == a) ans++;if (arr[2] == b) ans++;for (int j = 3; j <= 30; ++j) {c = a + b;//这里是一个减枝if (c > V) break;if (c == arr[j]) ans++;a = b;b = c;}res = Math.min(count - ans, res);}out.println(res);out.flush();}
}
2.C++
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int V=1000000;int n;
int arr[50];
int res=inf;
int main()
{scanf("%d",&n);int count=n;//只需要考虑前30位数if(n>30) n=30;for(int i=1;i<=n;++i){scanf("%d",&arr[i]);}//起始的数(f[1]的值)for(int i=1;i<=V;++i){//a,b,c作为滚动数组枚举斐波那契数LL a=i,b=i,c=0;int ans=0;if(arr[1]==a) ans++;if(arr[2]==b) ans++;for(int j=3;j<=30;++j){c=a+b;//没必要继续下去if(c>V) break;if(c==arr[j]) ans++;a=b,b=c;}res=min(count-ans,res);}printf("%d\n",res);return 0;
}
3.Python
v=1000000
res=float("inf")
n=int(input())
count=n
if n>30:n=30
arr=[0]*50
l=list(map(int,input().split()))
for i in range(1,n+1):arr[i]=l[i-1]
for i in range(1,v+1):a,b,c=i,i,0ans=0if arr[1]==a:ans=ans+1if arr[2]==b:ans=ans+1for j in range(3,31):c=a+bif c>v:breakif c==arr[j]:ans=ans+1a,b=b,cres=min(count-ans,res)
print(res)```
相关文章:

第十三届蓝桥杯国赛 C++ C 组 Java A 组 C 组 Python C 组 E 题——斐波那契数组(三语言代码AC)
目录1.斐波那契数组1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围7.原题链接2.解题思路3.Ac_code1.Java2.C3.Python1.斐波那契数组 1.题目描述 如果数组 A(a0,a1,⋯.an−1)A(a_0,a_1,⋯.a_{n-1})A(a0,a1,⋯.an−1)满足以下条件, 就说它是一个斐波那契…...
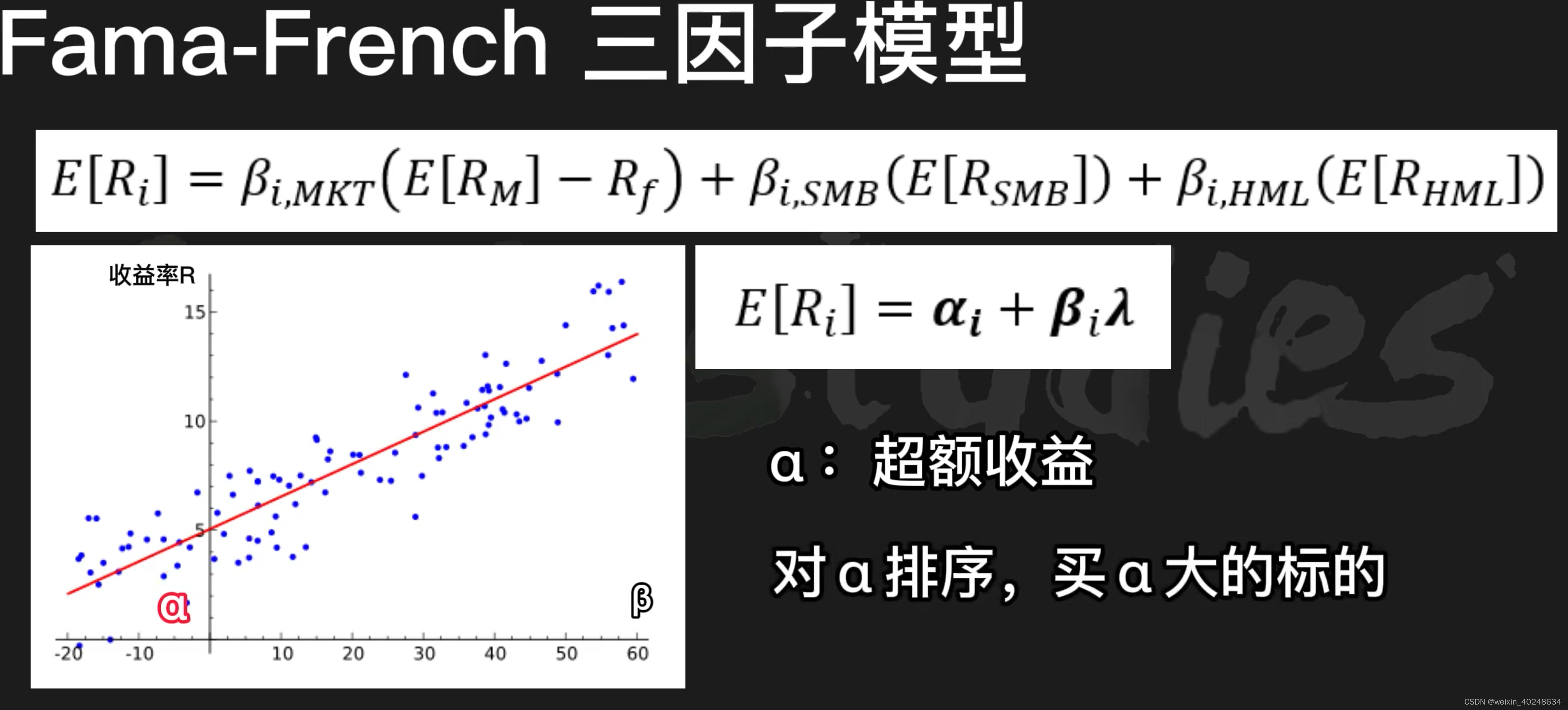
多因子模型(MFM)
多因子模型(Muiti-Factor M: MFM)因子投资基础CAPM (资本资产定价模型)APT套利定价理论截面数据 & 时间序列数据 & 面板数据定价误差 α\alphaαalpha 出现的原因线性多因子模型Fama-French三因子模型三因子的计算公式利用alpha大小进行购买股票…...

django项目实战一(django+bootstrap实现增删改查)
目录 一、创建django项目 二、修改默认配置 三、配置数据库连接 四、创建表结构 五、在app当中创建静态文件 六、页面实战-部门管理 1、实现一个部门列表页面 2、实现新增部门页面 3、实现删除部门 4、实现部门编辑功能 七、模版的继承 1、创建模板layout.html 1&…...
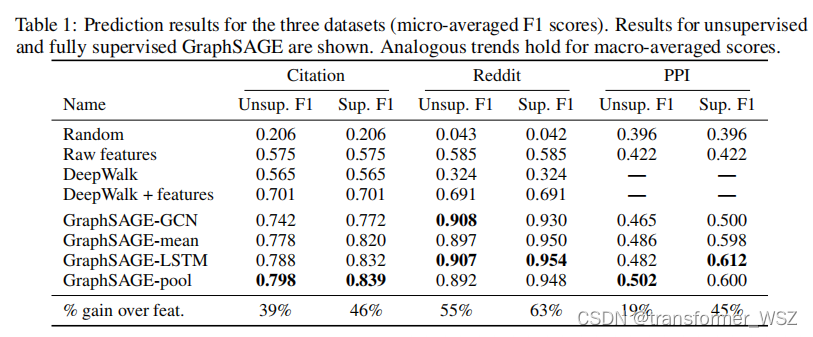
graphsage解读
传统的图方法都是直推式(transductive)的,学习到的是结构固定的图模型,一旦有新的节点加入,便需要重新训练整个图网络,泛化性不强。GraphSAGE是归纳式(inductive)的,它学习一种映射:通过采样和聚合邻居节点…...
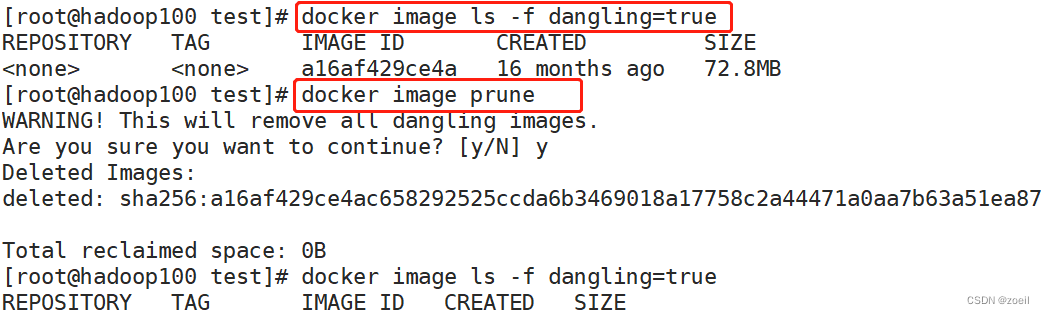
一文带你读懂Dockerfile
目录 一、概述 二、DockerFile构建过程解析 (一)Dockerfile内容基础知识 (二)Docker执行Dockerfile的大致流程 (三)总结 三、DockerFile常用保留字指令 四、案例 (一)自定义…...
用python实现对AES加密的视频数据流解密
密码学中的高级加密标准(Advanced Encryption Standard,AES),又称Rijndael加密法。 在做网络爬虫的时候,会遇到经过AES加密的数据,可以使用python来进行解密。 在做爬虫的时候,通常可以找到一个key,这个key是一个十六进制的一串字符,这传字符是解密的关键。所以对于…...

网络高可用方案
目录 1. 网络高可用 2. 高可用方案设计 2.1 方案一 堆叠 ha负载均衡模式 2.2 方案二 OSPF ha负载均衡模式 3. 高可用保障 1. 网络高可用 网络高可用,是指对于网络的核心部分或设备在设计上考虑冗余和备份,减少单点故障对整个网络的影响。其设计应…...

简单的认识 Vue(vue-cli安装、node安装、开发者工具)
Vue1、Vue 与其他框架的对比及特点1.1 Vue.js 是什么1.2 作者1.3 作用1.4 Vue 与其他框架的对比2、安装 Vue 的方法2.1 CDN 引入2.2 脚手架工具2.3 vue 开发者工具安装3、创建第一个实例4、理解 Vue 的 MVVM 模式5、数据双向绑定5.1 感受响应式实验总结1、Vue 与其他框架的对比…...
如何写一个 things3 client
Things3[1] 是一款苹果生态内的任务管理软件,是一家德国公司做的,非常好用。我前后尝试了众多任务管理软件,最终选定 things3,以后有机会会写文章介绍我是如何用 things3 来管理我的日常任务。本文主要介绍欧神写的 tli[2] 工具来…...

人工智能原理复习 | 命题逻辑和谓词演算
文章目录 一、前言二、命题逻辑三、谓词逻辑CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 数理逻辑思想的起源:莱布尼茨之梦。古典数理逻辑主要包括两部分:命题逻辑和谓词逻辑,命题逻辑又是谓词逻辑的一种简单情形。 逻辑研究的基本内容: 语法。语言部分:基…...
前端基础面试题:如何判断对象是否具有某属性?遍历数组的方法有哪些?
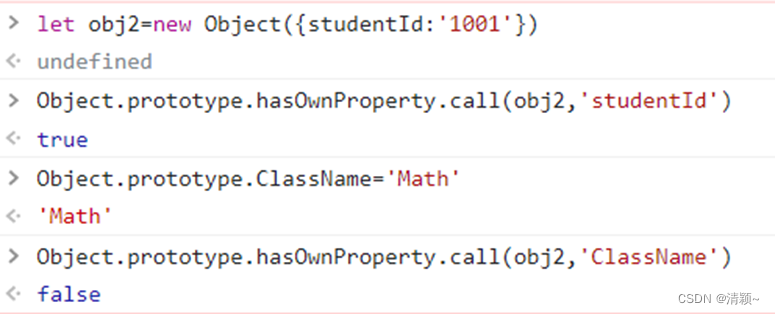
一、如何判断对象具有某属性? 如:let obj{name:zhangsan,age:21} 有以下方法 ( property 为属性名的变量,实际上是key,键名): 1. property in obj 效果如图: in 运算符 2. Reflect.has(obj, property)…...
Docker入门和安装教程
一、Docker入门简介 Docker 是一个基于GO语言开发的开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux机器上,也可以实现虚拟化。 容器是完全使用沙箱机制,相互之间不会…...
有了java基础,迅速学完Python并做了一份笔记-全套Python,建议收藏
面向过程Python简介Python和Java的解释方式对比Java:源代码 -> 编译成class -> Jvm解释运行Python:源代码 -> Python解释器解释运行我经常和身边的Java开发者开玩笑说:“Java真变态,别的语言都是要么直接编译要么直接解释…...
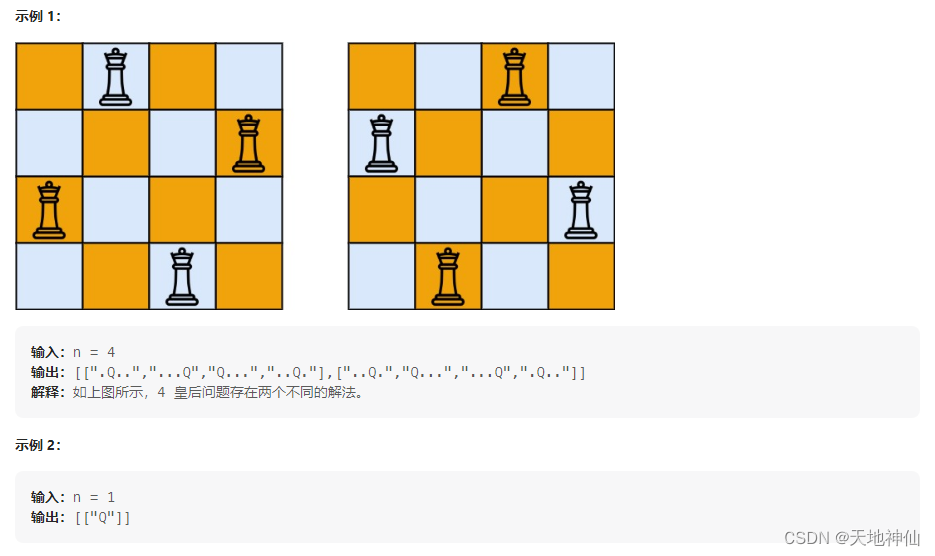
LeetCode——51. N 皇后
一、题目 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案…...

jQuery基本操作
学习目标: 会使用基本选择器获取元素 会使用层次选择器获取元素 会使用属性选择器获取元素 会使用过滤选择器获取元素 学习内容: 1.回顾jQuery语法结构 语法 $(selector).action; 工厂函数$():将DOM对象转化为jQuery对象。 选择器 sele…...
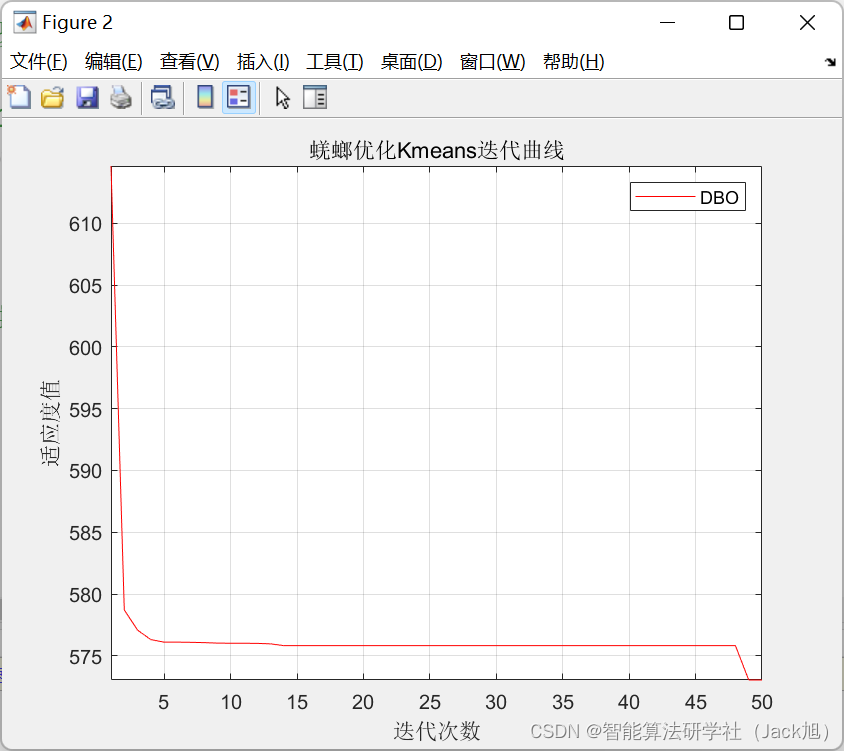
基于蜣螂算法优化Kmeans图像分割-附代码
基于蜣螂优化Kmeans图像分割算法 - 附代码 文章目录基于蜣螂优化Kmeans图像分割算法 - 附代码1.Kmeans原理2.基于蜣螂算法的Kmeans聚类3.算法实验结果4.Matlab代码摘要:基于蜣螂优化Kmeans图像分割算法。1.Kmeans原理 K-Means算法是一种无监督分类算法,…...
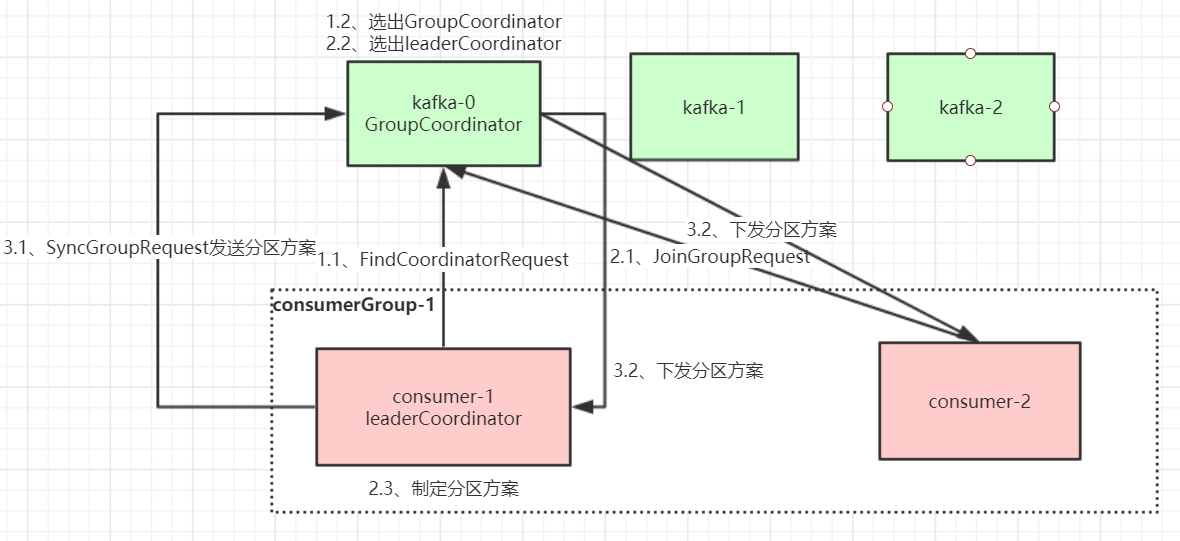
第二章 Kafka设计原理详解
第二章 Kafka设计原理详解 1、Kafka核心总控制器Controller 在 Kafka 集群中会有一个或者多个 broker,其中有一个 broker 会被选举为控制器(Kafka Controller),它负责管理整个集群中所有分区和副本的状态。 当某个分区的 leader…...

《NFL橄榄球》:费城老鹰·橄榄1号位
费城老鹰(英语:Philadelphia Eagles)是美国橄榄球联盟在宾夕法尼亚州费城的一支球队。1933年在国家橄榄球联盟扩编时与匹兹堡钢人和辛辛那提红人一起加入;1943年赛季因二次大战的缘故,和匹兹堡钢人作短暂的合并。 在20…...
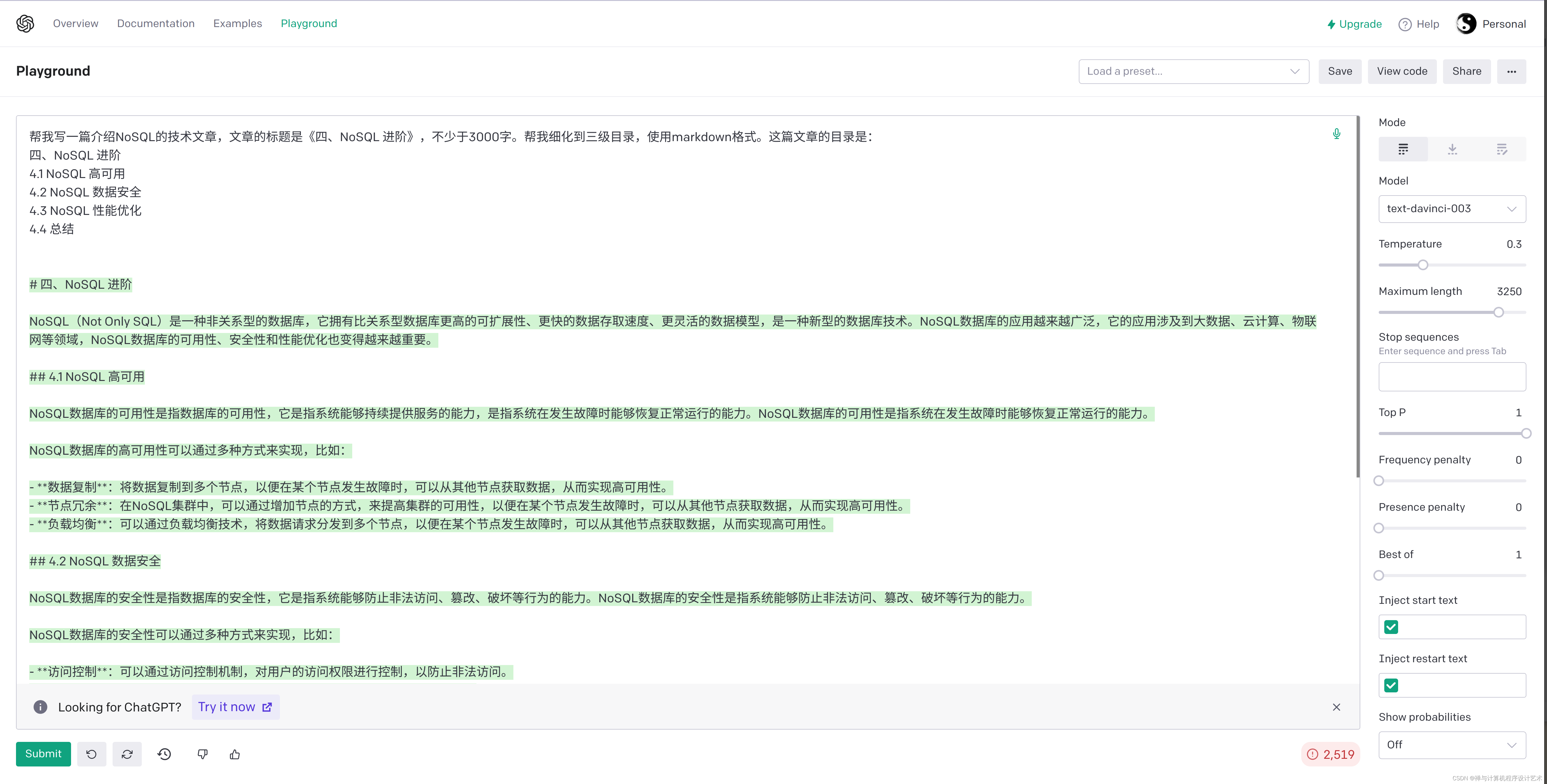
【人工智能AI】四、NoSQL进阶《NoSQL 企业级基础入门与进阶实战》
帮我写一篇介绍NoSQL的技术文章,文章的标题是《四、NoSQL进阶》,不少于3000字。帮我细化到三级目录,使用markdown格式。这篇文章的目录是: 四、NoSQL 进阶 4.1 NoSQL 高可用 4.2 NoSQL 数据安全 4.3 NoSQL 性能优化 4.4 总结 四、…...
K8S 部署 Jenkins
本文使用 bitnami 镜像部署 Jenkins 官方文档:https://github.com/bitnami/charts/tree/main/bitnami/jenkins 添加 bitnami 仓库 helm repo add bitnami https://charts.bitnami.com/bitnami自定义 values.yaml storageClass:集群的存储类ÿ…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
