【C++修炼之路】21.红黑树封装map和set
每一个不曾起舞的日子都是对生命的辜负
红黑树封装map和set
- 前言
- 一.改良红黑树的数据域结构
- 1.1 改良后的结点
- 1.2 改良后的类
- 二. 封装的set和map
- 2.1 set.h
- 2.2 map.h
- 三. 迭代器
- 3.1 迭代器封装
- 3.2 const迭代器
- 四.完整代码实现
- 4.1 RBTree.h
- 4.2 set.h
- 4.3 map.h
- 4.4 Test.cpp
前言
上一节中,说到了红黑树的实现,并且已经知道map和set的底层共用了同一套红黑树的结构。但这样就会出现一个问题,map的数据域和set不一样,比较大小的方式自然也就不一样。因此上一篇中的红黑树还需要做出一些改变才能用来实现map和set。
一.改良红黑树的数据域结构
对于如何设计针对map、set的红黑树结构,看源码的实现无疑是最好的方式:

对于源码的实现,我们知道set是<k,k>的键值对,但是在使用时却只显示一个k,map是<k,value>的键值对,通过观察源码发现,map的节点结构为
rb_tree<key_type, value_type>,但发现其设计方式很特殊,value_type是pair<const Key, T>的重命名,也就是说,map节点结构的key_type并不作为数据域,value_type单一类型就充当了数据域,而key_type实际上可以充当查找的作用。因此,下面改良红黑树就采用这种方式:一个类型T作为结点的全部数据域。
1.1 改良后的结点
enum Color//颜色采用枚举,但STL库采用的是特殊的bool值,后续会看
{RED,//0BLACK//1
};template<class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Color _col;RBTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}};
与之前的双参数<class K, class V>相比,改良之后的T作为了全部的数据域,即T也可以代表pair类型。
1.2 改良后的类
在前言中提到,比较方式也是一个头疼的问题,这个时候就可以自己封装一个比较方式,即以仿函数的形式进行比较。
由于只有比较方式进行了改变,因此除了insert其他的都没有变化,所以下面只展示insert
enum Color//颜色采用枚举,但STL库采用的是特殊的bool值,后续会看
{RED,//0BLACK//1
};template<class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Color _col;RBTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}};// set->RBTree<K, K, SetKeyOfT> _t;
// map->RBTree<K, pair<const K, V>, MapKeyOfT> _t;
template<class K, class T, class KeyOfT>//新增的KeyOfT就是仿函数
class RBTree
{typedef RBTreeNode<T> Node;
public:bool Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;//根节点为黑色return true;}KeyOfT kot;//仿函数Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data);cur->_col = RED;//重要,插入的结点初始化成红色if (kot(parent->_data) < kot(data)){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED)//如果父亲的颜色为红,才需要去处理{Node* grandfather = parent->_parent;//找到祖父才能找到叔叔if (parent == grandfather->_left){Node* uncle = grandfather->_right;//看叔叔颜色//情况1:uncle存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//情况2或3:不用考虑叔叔的问题,即叔叔为空还是为黑{if (cur == parent->_left)//情况2{// g// p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//情况3{// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//与上述代码的左右反过来了而已,步骤一样但左右相反。{Node* uncle = grandfather->_left;//情况1if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//情况2和3{// g// p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}}}}_root->_col = BLACK;return true;}
private:Node* _root = nullptr;
};二. 封装的set和map
以仿函数封装就可以完成比较。
2.1 set.h
#pragma once
#include"RBTree.h"namespace cfy
{template<class K>class set{struct SetKeyOfT//仿函数{const K& operator()(const K& key){return key;}};public:bool insert(const K& key){return _t.Insert(key);}private:RBTree<K, K, SetKeyOfT> _t;};void test_set(){int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };set<int> s;for (auto e : a){s.insert(e);}}
}
2.2 map.h
#pragma once
#include"RBTree.h"
namespace cfy
{template<class K, class V>class map{struct MapKeyOfT//仿函数{const K& operator()(const pair<const K, V>& kv){return kv.first;}};public:bool insert(const pair<const K, V>& kv){return _t.Insert(kv);}private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;};void test_map(){int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };map<int, int> m;for (auto e : a){m.insert(make_pair(e, e));}}
}
三. 迭代器
需要将有关迭代器的功能都封装起来,这在之前的vector、list模拟实现时已经了解过。对于map和set的迭代器,重要的函数重载就是++和–了。为了map和set能够共用这一套迭代器,因此将其封装在RBTree里。
3.1 迭代器封装
迭代器的好处是可以方便遍历,是数据结构的底层实现与用户透明。如果想要给红黑树增加迭代器,需要考虑以前问题:begin()与end()
STL明确规定,begin()与end()代表的是一段前闭后开的区间,而对红黑树进行中序遍历后,可以得到一个有序的序列,因此:begin()可以放在红黑树中最小节点(即最左侧节点)的位置,end()放在最大节点(最右侧节点)的下一个位置,关键是最大节点的下一个位置在哪块?
能否给成nullptr呢?答案是行不通的,因为对end()位置的迭代器进行–操作,必须要能找最后一个元素,此处就不行,因此最好的方式是将end()放在头结点的位置: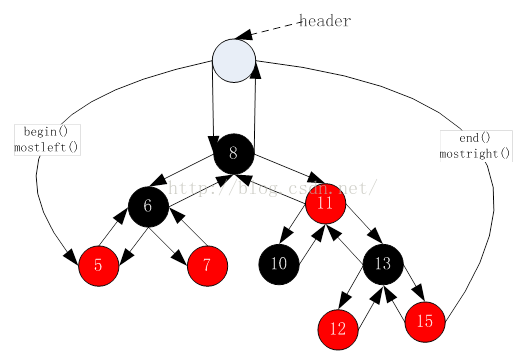
但由于我们上一届中设计的RBTree没有头结点这个结构,因此我们也就不与STL的实现方式完全一样,end()就直接设置为nullptr。
//迭代器
template<class T>
struct __RBTreeIterator
{typedef RBTreeNode<T> Node;typedef __RBTreeIterator<T> Self;//迭代器类进行typedefNode* _node;__RBTreeIterator(Node* node):_node(node){}T& operator*(){return _node->_data;}T* operator->(){return &_node->_data;}//迭代器++//迭代器--//上面两个都拿出来在下面bool operator!=(const Self& s){return _node != s._node;}};
一. 对于++,有这么两种选择:
- 如果右树不为空,则找到右树的最左节点。
- 如果右树为空,则找到孩子是父亲的左孩子的那个祖先。
Self& operator++()//迭代器返回的还是迭代器
{if (_node->_right)//1.右不为空,找到右子树的最左节点{Node* min = _node->_right;while (min->_left){min = min->_left;}_node = min;}else//2.右为空,则找祖先:孩子是父亲的左的那个祖先{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;
}
二. 对于–,有这么两种选择:(事实上思路就是与++相反)
- 如果左树不为空,则找到左树的最右结点(也就是最大结点)。
- 如果左树为空,则找到孩子是父亲的右孩子的那个祖先。
Self& operator--()
{if (_node->_left){Node* max = _node->_left;while (max->_right)//max一定存在,因此不需要写出max条件{max = max->_right;}_node = max;}else{Node* cur = _node;Node* parent = _node->_parent;while (parent && cur == parent->_left){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;
}
3.2 const迭代器
如果是const迭代器,那可以在迭代器类中多加上两个模板参数:T&, T*偏特化,当然实际上是Ref,Ptr的全特化;由于set不能修改,因此set的普通迭代器和const迭代器都应该是const类型,但map的value可以修改,因此我们就需要在RBTree中把普通迭代器和const迭代器均实现出来。此外,对于map来讲,需要实现operator[]的重载,因此我们插入函数返回的值也应该从bool变成pair类型,这样才便于在operator[]重载中进行操作。由于代码繁琐,且需要处理一些细节问题,因此代码的注释将会就那些进行解释,看下面代码就可以了。
四.完整代码实现
提示:需要注意细节问题,如普通迭代器可以赋值给const迭代器的原理。
4.1 RBTree.h
#pragma onceenum Color//颜色采用枚举,但STL库采用的是特殊的bool值,后续会看
{RED,//0BLACK//1
};template<class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Color _col;RBTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}};//迭代器
// class< T, T&, T*>
template<class T, class Ref, class Ptr>
struct __RBTreeIterator
{typedef RBTreeNode<T> Node;typedef __RBTreeIterator<T, Ref, Ptr> Self;//迭代器类进行typedef//如果Ref和Ptr都是非const,则下面与上面没区别,但如果是const,则下面仍是非const,因此可以const迭代器可以赋值给非const就是因为下面的这个,就是一个构造typedef __RBTreeIterator<T, T&, T*> iterator;//满足普通迭代器可以赋值给const迭代器Node* _node;__RBTreeIterator(Node* node):_node(node){}// 普通迭代器的时候,他是拷贝构造// const迭代器的时候,他是构造,支持用普通迭代器构造const迭代器__RBTreeIterator(const iterator& s)//加上这个,就满足普通迭代器赋值给const迭代器:_node(s._node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}Self& operator++()//迭代器返回的还是迭代器{if (_node->_right)//1.右不为空,找到右子树的最左节点{Node* min = _node->_right;while (min->_left){min = min->_left;}_node = min;}else//2.右为空,则找祖先:孩子是父亲的左的那个祖先{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}Self& operator--(){if (_node->_left){Node* max = _node->_left;while (max->_right)//max一定存在,因此不需要写出max条件{max = max->_right;}_node = max;}else{Node* cur = _node;Node* parent = _node->_parent;while (parent && cur == parent->_left){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}bool operator!=(const Self& s) const{return _node != s._node;}};// set->RBTree<K, K, SetKeyOfT> _t;
// map->RBTree<K, pair<const K, V>, MapKeyOfT> _t;
template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:typedef __RBTreeIterator<T, T&, T*> iterator;typedef __RBTreeIterator<T, const T&, const T*> const_iterator;iterator begin(){Node* left = _root;while (left && left->_left){left = left->_left;}return iterator(left);}iterator end(){return iterator(nullptr);}const_iterator begin() const{Node* left = _root;while (left && left->_left){left = left->_left;}return const_iterator(left);}const_iterator end() const{return const_iterator(nullptr);}pair<iterator, bool> Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;//根节点为黑色return make_pair(iterator(_root), true);}KeyOfT kot;//仿函数Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return make_pair(iterator(cur), false);}}cur = new Node(data);Node* newnode = cur;//加上这个是为了pair返回值时return的时候需要返回,因为cue会变,因此记录一下这个结点cur->_col = RED;//重要,插入的结点初始化成红色if (kot(parent->_data) < kot(data)){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED)//如果父亲的颜色为红,才需要去处理{Node* grandfather = parent->_parent;//找到祖父才能找到叔叔if (parent == grandfather->_left){Node* uncle = grandfather->_right;//看叔叔颜色//情况1:uncle存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//情况2或3:不用考虑叔叔的问题,即叔叔为空还是为黑{if (cur == parent->_left)//情况2{// g// p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//情况3{// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//与上述代码的左右反过来了而已,步骤一样但左右相反。{Node* uncle = grandfather->_left;//情况1if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//情况2和3{// g// p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}}}}_root->_col = BLACK;return make_pair(iterator(newnode), true);}//旋转代码和AVL一样,只是去掉了平衡因子void RotateL(Node* parent)//左单旋{//1.记录subR, subRLNode* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)//subRL不为空则需要连接到parent{subRL->_parent = parent;}Node* ppNode = parent->_parent;//记录保存subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr)//说明根节点变化{_root = subR;_root->_parent = nullptr;}else//如果是局部子树{//判断ppNode之前是左连接还是右连接if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void Inorder(){_Inorder(_root);}bool IsBalance()//检查是否为红黑树结构{if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK){++ref;}left = left->_left;}//遍历这棵树,就好了,检查是否存在连续的红结点。//检查父亲,因为孩子不一定有,但是一定有父亲return Check(_root, 0, ref);}private:bool Check(Node* root, int blackNum, int ref){if (root == nullptr){if (blackNum != ref){cout << "违反规则:一条路径上的黑色节点数量不同" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则,出现连续红色结点" << endl;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);}void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}Node* _root = nullptr;
};4.2 set.h
#pragma once
#include"RBTree.h"namespace cfy
{template<class K>class set{struct SetKeyOfT{const K& operator()(const K& key){return key;}};public://加上typename是由于没有实例化的模板不能进行typedef。由于不能修改,因此均用consttypedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;iterator begin() const{return _t.begin();//_t.begin()是普通迭代器,iterator是const,因此需要修改}iterator end() const{return _t.end();}pair<iterator, bool> insert(const K& key){//直接return会造成const与非const的类型不匹配//因为set的iterator默认就是const,但return的并不是const//因此需要如下修正:pair<typename RBTree<K, K, SetKeyOfT>::iterator, bool> ret = _t.Insert(key);return pair<iterator, bool>(ret.first, ret.second);}private:RBTree<K, K, SetKeyOfT> _t;};void test_set(){int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };set<int> s;for (auto e : a){s.insert(e);}set<int>::iterator it = s.begin();while (it != s.end()){//*it += 10;//set这里不能被修改,因此const迭代器统一cout << *it << " ";++it;}cout << endl;for (auto& e : s){cout << e << " ";}cout << endl;}
}
4.3 map.h
#pragma once
#include"RBTree.h"
namespace cfy
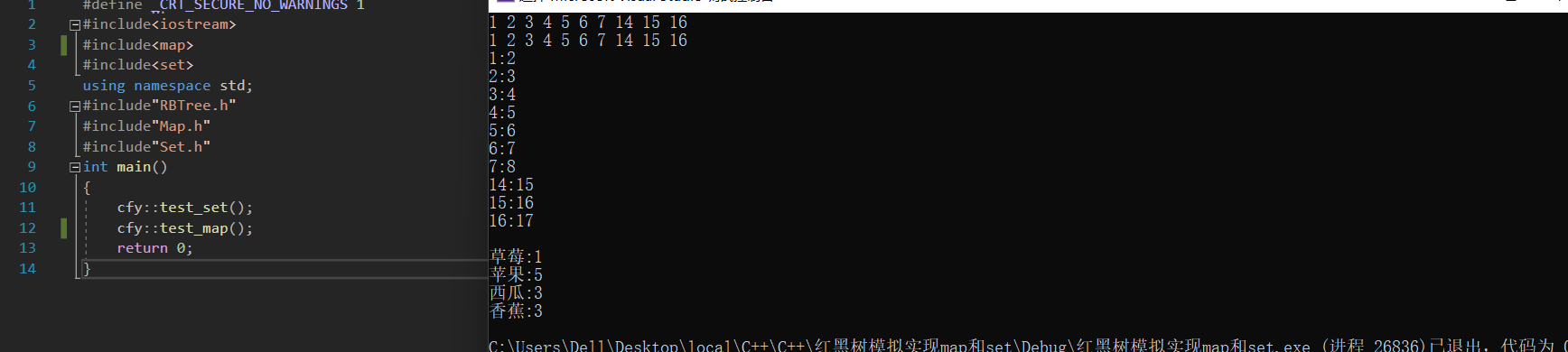
{template<class K, class V>class map{struct MapKeyOfT{const K& operator()(const pair<const K, V>& kv){return kv.first;}};public://加上typename是由于没有实例化的模板不能进行typedef。typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}const_iterator begin() const{return _t.begin();}const_iterator end() const{return _t.end();}pair<iterator, bool> insert(const pair<const K, V>& kv){return _t.Insert(kv);}V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}private:RBTree<K, pair<const K, V>, MapKeyOfT> _t;};void test_map(){int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };map<int, int> m;for (auto e : a){m.insert(make_pair(e, e));}map<int, int>::iterator it = m.begin();while (it != m.end()){//it->first++; 经过const就不能修改了it->second++;//允许被修改cout << it->first << ":" << it->second << endl;++it;}cout << endl;//map统计水果操作的次数string arr[] = { "苹果", "西瓜", "香蕉", "草莓", "西瓜","苹果", "苹果","西瓜","苹果", "香蕉", "苹果", "香蕉" };map<string, int> countMap;for (auto& e : arr){countMap[e]++;}for (const auto& kv : countMap)//注意加引用,不给就是拷贝构造,代价大{cout << kv.first << ":" << kv.second << endl;}}
}
4.4 Test.cpp
#include<iostream>
#include<map>
#include<set>
using namespace std;
#include"RBTree.h"
#include"Map.h"
#include"Set.h"
int main()
{cfy::test_set();cfy::test_map();return 0;
}
相关文章:

【C++修炼之路】21.红黑树封装map和set
每一个不曾起舞的日子都是对生命的辜负 红黑树封装map和set前言一.改良红黑树的数据域结构1.1 改良后的结点1.2 改良后的类二. 封装的set和map2.1 set.h2.2 map.h三. 迭代器3.1 迭代器封装3.2 const迭代器四.完整代码实现4.1 RBTree.h4.2 set.h4.3 map.h4.4 Test.cpp前言 上一节…...

下载ojdbc14.jar的10.2.0.1.0版本的包
一、首先要有ojdbc14.jar包 没有的可以去下载一个,我的是从这里下载的ojdbc14.jar下载_ojdbc14.jar最新版下载[驱动包软件]-下载之家, 就是无奈关注了一个公众号,有的就不用下了。 二、找到maven的本地仓库的地址 我的地址在这里D:\apach…...

关于欧拉角你需要知道几个点
基础理解,参照:https://www.cnblogs.com/Estranged-Tech/p/16903025.html 欧拉角、万向节死锁(锁死)理解 一、欧拉角理解 举例讲解 欧拉角用三次独立的绕确定的轴旋转角度来表示姿态。如下图所示 经过三次旋转,旋…...
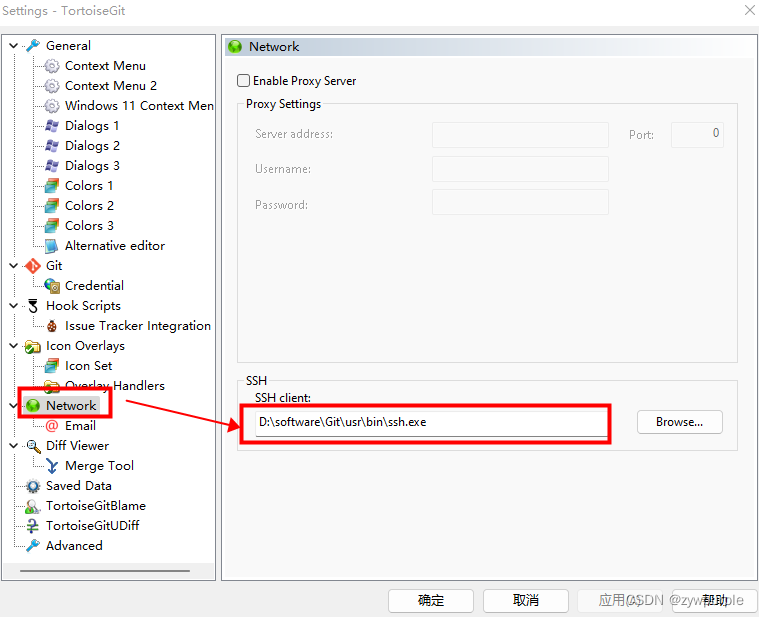
git ssh配置
ssh配置 执行以下命令进行配置 git config --global user.name “这里换上你的用户名” git config --global user.email “这里换上你的邮箱” 执行以下命令生成秘钥: ssh-keygen -t rsa -C “这里换上你的邮箱” 执行命令后需要进行3次或4次确认。直接全部回车就…...
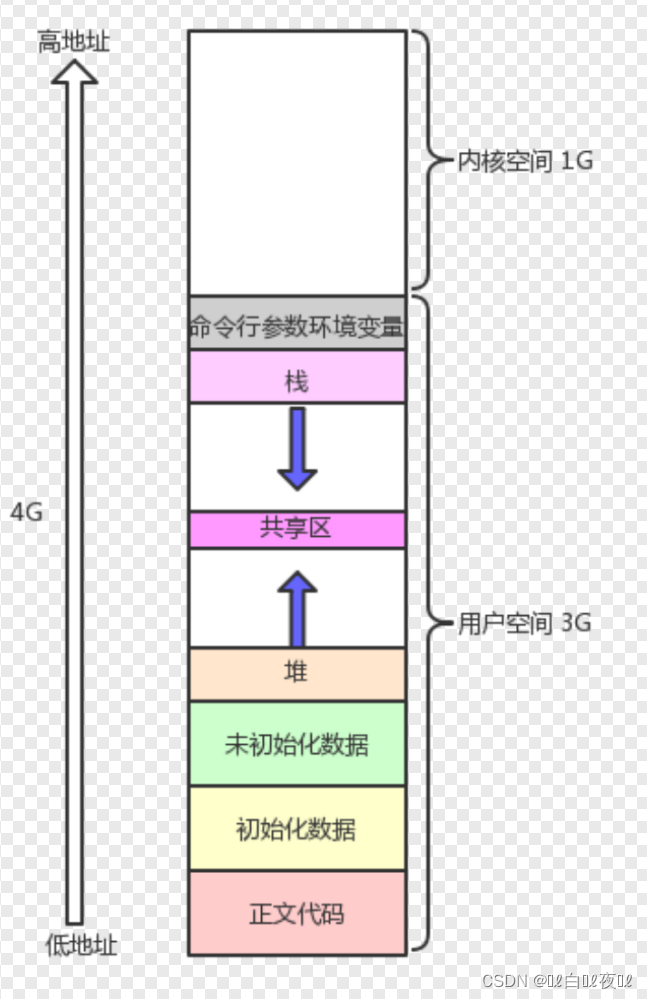
Linux进程概念(三)
环境变量与进程地址空间环境变量什么是环境变量常见环境变量环境变量相关命令环境变量的全局属性PWDmain函数的三个参数进程地址空间什么是进程地址空间进程地址空间,页表,内存的关系为什么存在进程地址空间环境变量 什么是环境变量 我们所有写的程序都…...

新手福利——x64逆向基础
一、x64程序的内存和通用寄存器 随着游戏行业的发展,x32位的程序已经很难满足一些新兴游戏的需求了,因为32位内存的最大值为0xFFFFFFFF,这个值看似足够,但是当游戏对资源需求非常大,那么真正可以分配的内存就显得捉襟…...
)
虚幻c++中的细节之枚举类型(enum)
文章目录前言一、原生c的枚举类型关键字classint8 - 枚举的基础类型(underlying type)二、枚举类型的灵活运用位运算枚举循环遍历三、虚幻风格的枚举类型UENUMUMETATEnumAsByte总结前言 虚幻引擎中的代码部分实现了一套反射机制,为c代码带了…...

判断某个字符串在另一个字符串中的个数
/** * 用于判断字符串中字符的个数 * * param str1 原字符串 * param str2 需要判断的字符 * return 返回有几个 */ private int getCount(String str1, String str2) { //获取两个字符串的长度 int oneLength str1.length(); int toLength str2.length(); //定义两个整数&am…...

测试人员如何运用好OKR
在软件测试工作中是不是还不知道OKR是什么?又或者每次都很害怕写OKR?或者总觉得很迷茫,不知道目标是什么? OKR 与 KPI 的区别 去年公司从KPI换OKR之后,我也有一段抓瞎的过程,然后自己找了两本书看,一本是《OKR工作法》…...

CentOS7 Hive2.3.9 安装部署(mysql 8.0)
一、CentOS7安装MySQL数据库 查询载mariadb rpm -qa | grep mariadb卸载mariadb rpm -e --nodeps [查询出来的内容]安装wget为下载mysql准备 yum -y install wget在tools目录下执行以下命令,下载MySQL的repo源: wget -P /tools/ https://dev.mysql.…...
)
【PTA Advanced】1142 Maximal Clique(C++)
目录 题目 Input Specification: Output Specification: Sample Input: Sample Output: 思路 代码 题目 A clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. A maximal clique is a clique …...

1. MySQL在金融互联网行业的企业级安装部署
这里写目录标题 1. 版本介绍示例2.安装MySQL规范(建议二进制)2.1 安装方式2.2 安装用户2.3 目录规范3.二进制安装3.1 操作系统配置3.2 MySQL 5.7.33 安装部署2.3 MySQL8.0.27安装2.4 源码安装(了解 )3.多实例部署及注意事项3.1 多实例概念3.2 多实例安装3.3 多实例第二种方式…...

【C++修炼之路】19.AVL树
每一个不曾起舞的日子都是对生命的辜负 AVL树前言:一.AVL树的概念二.AVL树的结构2.1 AVL树节点的定义2.2 AVL树的结构2.3 AVL树的插入2.4 AVL树的验证2.5 AVL树的删除(了解)三.AVL树的旋转(重要)3.1 左单旋3.2 右单旋3.3 左右双旋3.4 右左双旋…...
项目管理工具dhtmlxGantt甘特图入门教程(十):服务器端数据集成(下)
这篇文章给大家讲解如何利用dhtmlxGantt在服务器端集成数据。 dhtmlxGantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表,可满足应用程序的所有需求,是完善的甘特图图表库 DhtmlxGantt正版试用下载(qun 764149912)http…...
LeetCode 793. 阶乘函数后 K 个零
f(x) 是 x! 末尾是 0 的数量。回想一下 x! 1 * 2 * 3 * ... * x,且 0! 1 。 例如, f(3) 0 ,因为 3! 6 的末尾没有 0 ;而 f(11) 2 ,因为 11! 39916800 末端有 2 个 0 。 给定 k,找出返回能满足 f(x) …...
maven打包顺序与jvm类加载顺序
背景:一次dev测试过程中,发现代码中关于jsr303的校验失效,校验类如下,会报一个莫名其妙的运行时错误;遂进行排查。import javax.validation.constraints.NotBlank;Data Accessors(chain true) public class Demo {Not…...

④ 链表
24. 两两交换链表中的节点 题目链接:https://leetcode.cn/problems/swap-nodes-in-pairs/ 注意点: 遍历链表的时候什么时候截止(避免空指针异常或无限死循环的问题)? 节点数量为偶数或链表为空时,cur.ne…...
小孩扁桃体肿大3度能自愈吗?6岁小孩扁桃体肥大怎么治效果好?
12月7日,四川眉山市民唐先生说,他刚出生的儿子在妇产医院分娩中心住了20天后感染了败血症。据唐先生介绍,哈子出院时各项指标正常。他在分娩中心住了半个月左右,孩子喝牛奶很生气,第二天就开始发烧了。同一天ÿ…...
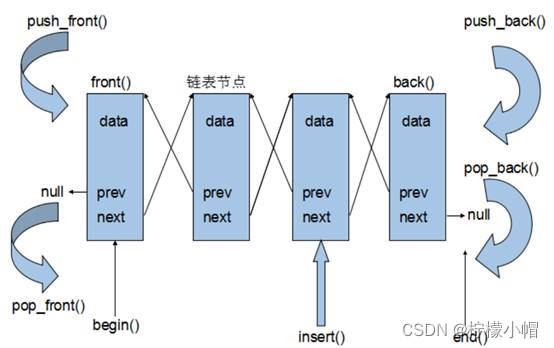
【C++提高编程】C++全栈体系(二十二)
C提高编程 第三章 STL - 常用容器 五、stack容器 1. stack 基本概念 概念:stack是一种先进后出(First In Last Out,FILO)的数据结构,它只有一个出口 栈中只有顶端的元素才可以被外界使用,因此栈不允许有遍历行为 栈中进入数据称为 — 入…...
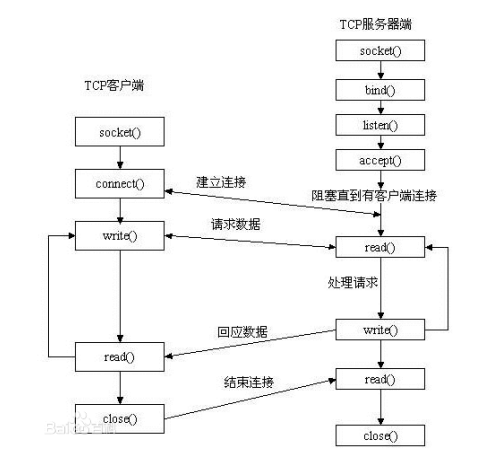
linux系统编程2--网络编程socket知识
在linux系统编程中网络编程是使用socket(套接字),socket这个词可以表示很多概念:在TCP/IP协议中,“IP地址TCP或UDP端口号”唯一标识网络通讯中的一个进程,“IP地址端口号”就称为socket。在TCP协议中&#…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

