时间复杂度
一、时间复杂度
时间复杂度是计算机科学中用来衡量算法运行时间随输入规模增加而增长的速度。简单来说,它是一个衡量算法执行效率的指标,表示算法运行所需时间与输入数据量之间的关系。
时间复杂度通常用大O符号(O)来表示,例如:O(1)、O(n)、O(n^2)等。这些符号描述了算法在最坏情况下执行的时间与输入规模之间的关系。其中:
-
O(1) 表示算法的执行时间是常数,不随输入规模变化而变化。即使输入数据量增加,算法的执行时间也保持恒定。
-
O(n) 表示算法的执行时间与输入规模线性增长,即输入规模增加一倍,执行时间也增加一倍。
-
O(n^2) 表示算法的执行时间与输入规模的平方成正比,即输入规模增加一倍,执行时间会增加四倍。
时间复杂度的理解帮助我们评估不同算法的效率,我们会尽量选择时间复杂度较低的算法,以获得更快的执行速度。
时间复杂度是对算法执行时间的一个抽象估计,它并不考虑硬件和编译器等因素对执行时间的影响。因此,时间复杂度只是一种相对的比较方式,而不是精确的执行时间。
二、(O)表达式含义
O(1)、O(n)、O(n^2) 等是描述算法时间复杂度的表示方式,它们反映了算法执行时间与输入规模的关系。以下是这些符号的具体定义:
-
O(1):常数时间复杂度。表示算法的执行时间是一个常数,不随输入规模的增加而改变。无论输入数据量多少,执行时间都保持恒定。
-
O(n):线性时间复杂度。表示算法的执行时间与输入规模成线性关系。如果输入数据量增加一倍,执行时间也会增加一倍。
-
O(n^2):平方时间复杂度。表示算法的执行时间与输入规模的平方成正比。如果输入数据量增加一倍,执行时间会增加四倍。
-
O(log n):对数时间复杂度。表示算法的执行时间与输入规模的对数成正比。在每一步操作中,算法可以将问题规模减少一半。
-
O(n log n):线性对数时间复杂度。表示算法的执行时间与输入规模的对数和线性的乘积成正比。常见于某些高效的排序算法,如:快速排序和归并排序。
-
O(m*n):多项式时间复杂度。表示算法的执行时间与输入规模的两个不同维度成正比。这是一种常见的在多维数据结构中的复杂度。
这些时间复杂度表示法帮助我们对不同算法的性能进行比较和评估,选择合适的算法来解决特定的问题。在进行算法分析和设计时,了解时间复杂度的含义和计算方法非常重要。
三、在实际过程中,如何估算时间复杂度?
在实际过程中,估算算法的时间复杂度可以通过以下方法进行:
-
计数基本操作: 首先,识别算法中的基本操作,如循环、条件判断、赋值等。然后,对这些基本操作进行计数,以了解算法在执行过程中涉及的基本操作次数。
-
确定输入规模: 确定算法的输入规模,通常用变量 n 表示。这可以是数据集的大小、数组的长度、输入元素的数量等。
-
分析循环次数: 如果算法中包含循环结构,分析循环的迭代次数。这通常涉及到输入规模 n,并考虑最坏情况下循环的迭代次数。
-
建立复杂度表达式: 将基本操作次数表示为输入规模 n 的函数,然后使用大O符号来表示算法的时间复杂度。
-
简化表达式: 对复杂度表达式进行简化,通常只保留最高项,去掉低次项和常数项。这样可以得到更为简洁的复杂度表示。
-
评估最坏情况: 时间复杂度通常估算算法在最坏情况下的执行时间。因此,需要考虑循环、条件等结构在最坏情况下的操作次数。
-
进行渐进分析: 时间复杂度分析更关注随着输入规模增加,算法执行时间的增长趋势。因此,进行渐进分析,关注算法的增长率。
-
比较不同算法: 如果有多个算法可以解决同一个问题,比较它们的时间复杂度,选择复杂度更低的算法。
-
实际测试验证: 估算的时间复杂度可以通过实际的测试和性能分析来验证。运行算法在不同输入规模下的实际执行时间,与估算的时间复杂度进行比较。
需要注意的是,时间复杂度是对算法执行时间的一个抽象估计,它不考虑具体硬件、编译器等因素对执行时间的影响。因此,在实际应用中,估算的时间复杂度可以作为指导,但实际执行时间可能会受到多种因素的影响。
四、案例分析
当分析时间复杂度时,让我们考虑以下几个案例:
-
案例:线性查找
def linear_search(arr, target):for num in arr:if num == target:return Truereturn False在这个案例中,我们有一个线性查找算法,它遍历数组来查找目标元素。最坏情况下,如果目标元素不在数组中,需要遍历整个数组。因此,时间复杂度为 O(n),其中 n 是数组的长度。
-
案例:插入排序
def insertion_sort(arr):for i in range(1, len(arr)):key = arr[i]j = i - 1while j >= 0 and arr[j] > key:arr[j + 1] = arr[j]j -= 1arr[j + 1] = key插入排序算法将数组中的元素逐个插入已排序的部分。在最坏情况下,当数组逆序排列时,每个元素都需要移动到数组的开头,因此需要执行更多操作。时间复杂度为 O(n^2),其中 n 是数组的长度。
-
案例:归并排序
def merge_sort(arr):if len(arr) > 1:mid = len(arr) // 2left_half = arr[:mid]right_half = arr[mid:]merge_sort(left_half)merge_sort(right_half)i = j = k = 0while i < len(left_half) and j < len(right_half):if left_half[i] < right_half[j]:arr[k] = left_half[i]i += 1else:arr[k] = right_half[j]j += 1k += 1while i < len(left_half):arr[k] = left_half[i]i += 1k += 1while j < len(right_half):arr[k] = right_half[j]j += 1k += 1归并排序算法将数组分成两半,递归地排序每个子数组,然后将它们合并。无论输入数据的顺序如何,归并排序的时间复杂度始终为 O(n log n)。
这些案例展示了不同类型的算法及其时间复杂度。通过对基本操作次数和输入规模的分析,我们可以更好地理解不同算法的效率和性能。
相关文章:

时间复杂度
一、时间复杂度 时间复杂度是计算机科学中用来衡量算法运行时间随输入规模增加而增长的速度。简单来说,它是一个衡量算法执行效率的指标,表示算法运行所需时间与输入数据量之间的关系。 时间复杂度通常用大O符号(O)来表示&#…...

Unity实现广告滚动播放、循环播放、鼠标切换的效果
效果: 场景结构: 特殊物体:panel下面用排列组件horizent layout group放置多个需要显示的面板,用mask遮罩好。 using System.Collections; using System.Collections.Generic; using DG.Tweening; using UnityEngine; using Unity…...
LangChain + Streamlit + Llama:将对话式AI引入本地机器
推荐:使用 NSDT场景编辑器 助你快速搭建可二次编辑的3D应用场景 什么是LLMS? 大型语言模型 (LLM) 是指能够生成与人类语言非常相似的文本并以自然方式理解提示的机器学习模型。这些模型使用包括书籍、文章、网站和其他来源在内的…...

Python 读写 Excel 文件库推荐和使用教程
文章目录 前言Python 读写 Excel 库简介openpyxl 处理 Excel 文件教程pandas 处理 Excel 文件教程总结 前言 Python 读写 Excel 文件的库总体看还是很多的, 各有其优缺点, 以下用一图总结各库的优缺点, 同时对整体友好的库重点介绍其使用教程…...

“深入解析JVM:理解Java虚拟机的工作原理和优化技巧“
标题:深入解析JVM:理解Java虚拟机的工作原理和优化技巧 摘要:本文将深入探讨Java虚拟机(JVM)的工作原理和优化技巧。我们将从JVM的基本结构开始,逐步介绍其工作原理,并提供一些实际示例代码&am…...
解决SEGGER Embedded Studio无法显示Nordic MCU外设寄存器问题
如果使用SES调试NRF52840的时候发现,官方例程只能显示CPU寄存器,但是无法显示外设寄存器时,解决办法如下: 1.在解决方案右键→Options→Debug→Debugger,然后Target Device选择正确的型号。 2.Register Definition Fil…...

Oracle-day1:scott用户、查询、取整、截取、模糊查询、别名——23/8/23
整理一下第一天软件测试培训的知识点 1、scott用户 -- 以system管理员登录锁定scott用户 alter user scott account lock;-- 以system管理员登录解锁scott用户 alter user scott account unlock;-- 以system管理员用户设置scott用户密码 alter user scott identfied by tiger…...
stm32之3.key开关
假设key电阻为40kΩ,则key0 的电压3.3v*4/52.64v 2.key开关代码 ② GPIO_OType_PP//推挽输出 GPIO_OType_PP//开漏输出 推挽输出是指输出端口可以同时提供高电平和低电平输出,而开漏输出则是指输出端口只能提供低电平输出,高电平时需要借…...

GPT带我学-设计模式-代理模式
什么是代理模式 代理模式(Proxy Pattern)是设计模式中的一种结构型模式,它为其他对象提供一种代理以控制对这个对象的访问。 代理模式有三个主要角色:抽象主题(Subject)、真实主题(Real Subje…...
VMware Workstation Pro 无法使用开机状态下拍的快照来克隆虚拟机,怎么解决?
环境: VMware Workstation Pro16.0 Win10 专业版 问题描述: VMware Workstation Pro有台虚拟机在开机状态下拍了个6.7快照这个win10初始版,现在想在这个快照下直接克隆,无法使用开机状态下拍的快照创建克隆 解决方案: 1.关闭当前虚拟机 2.到虚拟机文件夹复制一份Wind…...

【JAVA】XML及其解析技术、XML检索技术、设计模式
XML XML(Extensible Markup Language)是可扩展标记语言的缩写,它是一种数据表示格式,可以描述复杂的数据结构,常用于传输和存储数据 作用: 用于进行存储数据和传输数据作为软件的配置文件 第一行是文档声明 <?xml version&q…...
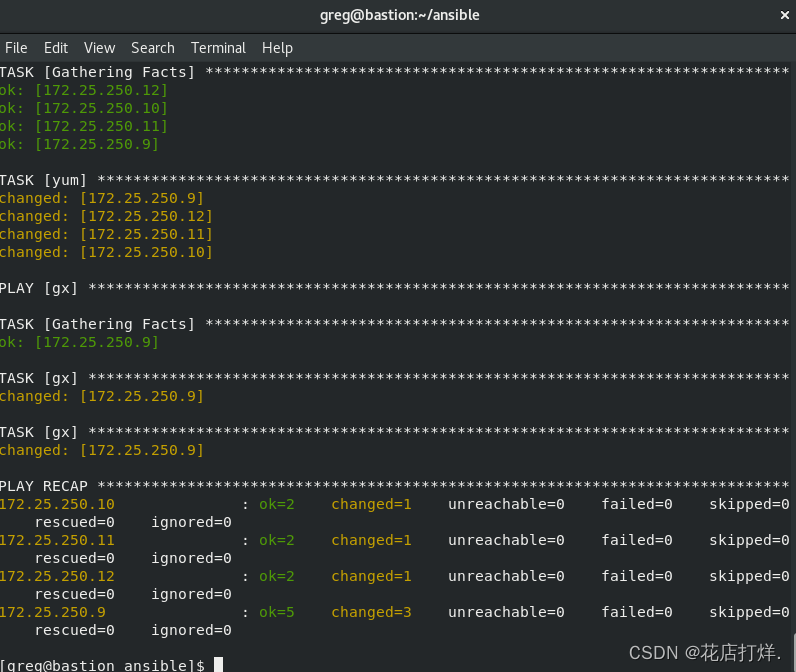
Ansible 自动化安装软件
例子如下: 创建一个名为/ansible/package.yml 的 playbook : 将 php 和 mariadb 软件包安装到 dev、test 和 prod 主机组中的主机上 将 RPM Development Tools 软件包组安装到 dev 主机组中的主机上 将 dev 主机组中主机上的所有软件包更新为最新版本 --- - name:…...

简单介绍 React Native 整合 Formik 实现表单校验
Formik 是 React 和 React Native 开源表单库,Formik 负责处理重复且烦人的事情——跟踪值/错误/访问的字段、编排验证和处理提交——所以您不必这样做。而简化字段校验的话我们可以使用yup工具来实现。 首先安装Formik 和 Yup npm i formik npm i yupFormik 与 R…...
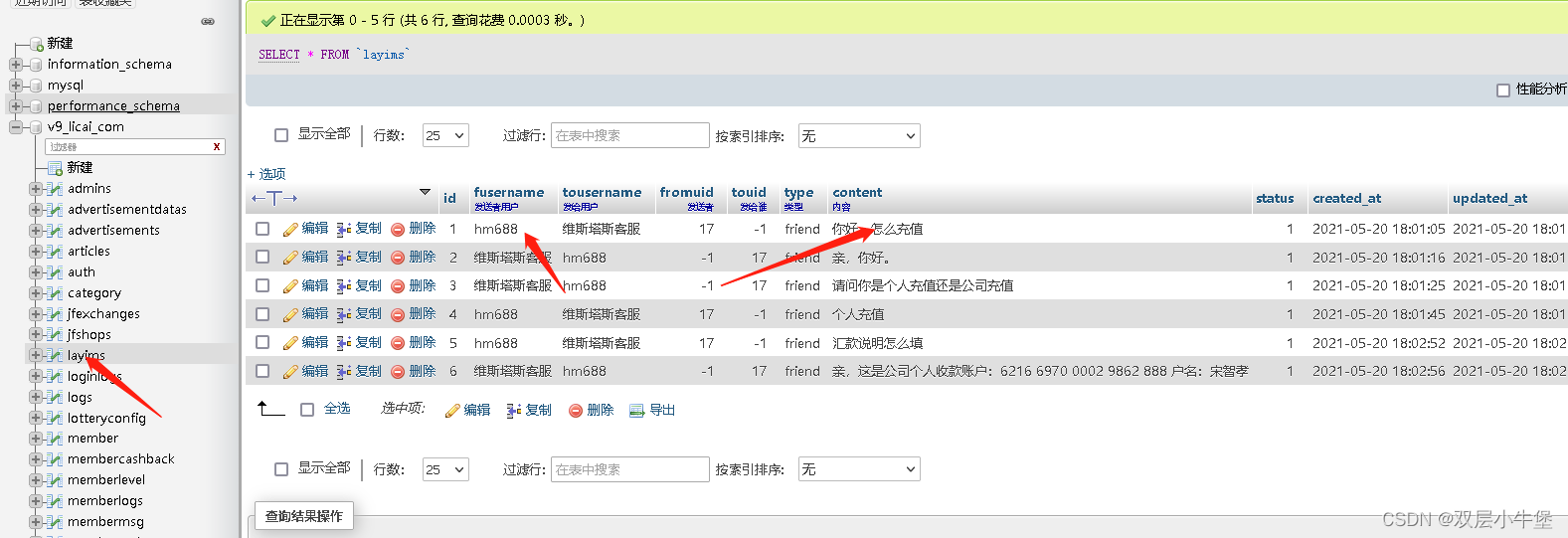
蓝帽杯半决赛2022
手机取证_1 iPhone手机的iBoot固件版本号:(答案参考格式:iBoot-1.1.1) 直接通过盘古石取证 打开 取证大师和火眼不知道为什么都无法提取这个 手机取证_2 该手机制作完备份UTC8的时间(非提取时间):(答案…...

电路学习+硬件每日学习十个知识点(40)23.8.20 (希腊字母读音,阶跃信号和冲激信号的关系式,信号的波形变换,信号的基本运算,卷积积分,卷积和)
文章目录 1.信号具有时间特性和频率特性。2.模拟转数字,抽样、量化、编码3.阶跃信号和冲激信号4.信号的波形变换(时移、折叠、尺度变换)5.信号的基本运算(加减、相乘、微分与积分、差分与累加)5.1 相加减5.2 相乘5.3 微…...

Python——列表(list)推导式
本文基于python3。 目录 1、Python推导式2、列表(list)推导式2.1、定义2.2、实际操作2.2.1、一个表达式,后面为一个 for 子句2.2.2、一个表达式,后面为一个 for 子句,然后,跟着if 子句。2.2.3、一个表达式,后面为一个…...

代码随想录算法训练营day43 | LeetCode 1049. 最后一块石头的重量 II 494. 目标和 474. 一和零
1049. 最后一块石头的重量 II(题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台) 思路:把全部石头重量加起来,然后除以二,就等于背包的最大容量。然后就可以按照背包问题…...
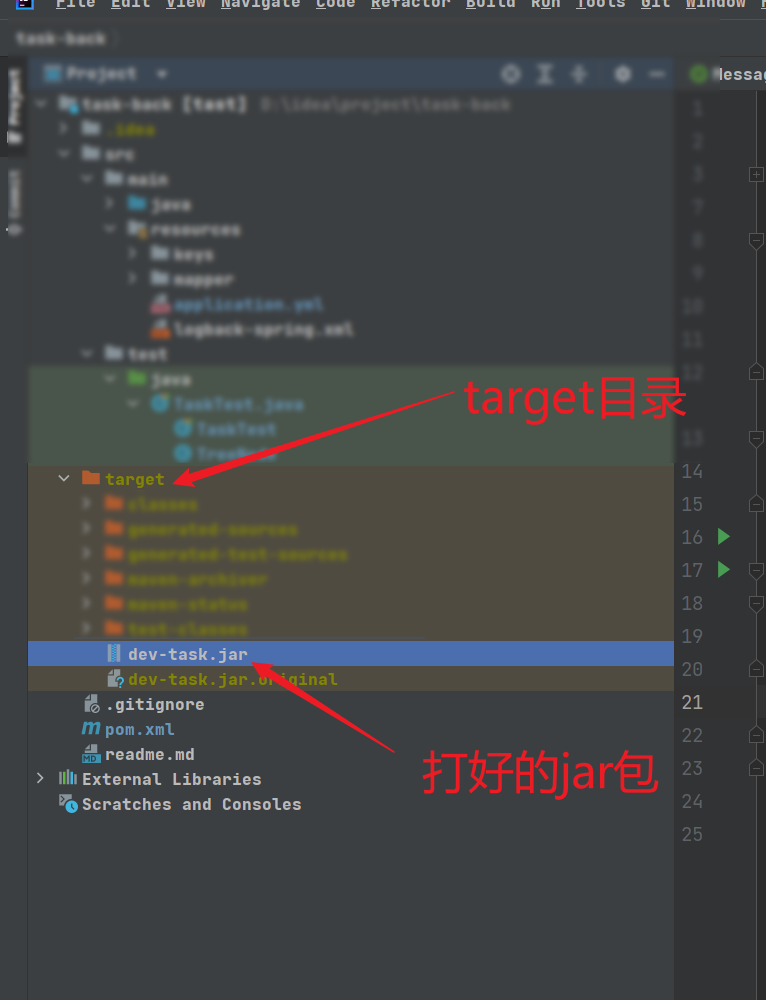
Linux安装jdk、mysql、并部署Springboot项目
😜作 者:是江迪呀✒️本文关键词:Linux、环境安装、JDK安装、MySQL、MySQL安装☀️每日 一言:知行合一! 文章目录 一、前言二、安装步骤2.1 安装JDK(1)创建文件夹(便于后…...
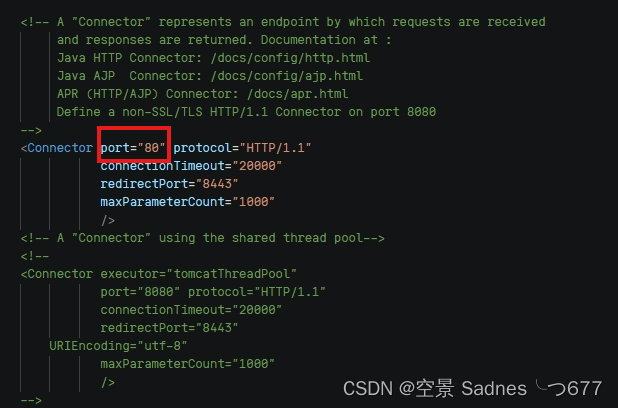
tomcat更改端口号和隐藏端口号
因为默认端口:8080不会自动隐藏,因此为了更显格调需要将其改为:80 进入tomcat的server文件 将其改为80,之后将tomcat重新启动即可 tomcat启动流程 [rootshang ~]# cd /usr/local/tomcat/apache-tomcat-8.5.92 [rootshang apache-tomcat-8.5.92]# cd b…...

生信分析Python实战练习 2 | 视频19
开源生信 Python教程 生信专用简明 Python 文字和视频教程 源码在:https://github.com/Tong-Chen/Bioinfo_course_python 目录 背景介绍 编程开篇为什么学习Python如何安装Python如何运行Python命令和脚本使用什么编辑器写Python脚本Python程序事例Python基本语法 数…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...
