当前位置： 首页 > news >正文

电路学习+硬件每日学习十个知识点（40）23.8.20 （希腊字母读音，阶跃信号和冲激信号的关系式，信号的波形变换，信号的基本运算，卷积积分，卷积和）

news 2026/2/9 3:14:31

文章目录

  • 1.信号具有时间特性和频率特性。
  • 2.模拟转数字，抽样、量化、编码
  • 3.阶跃信号和冲激信号
  • 4.信号的波形变换（时移、折叠、尺度变换）
  • 5.信号的基本运算（加减、相乘、微分与积分、差分与累加）
    • 5.1 相加减
    • 5.2 相乘
    • 5.3 微分与积分
    • 5.4 差分与累加
  • 6.卷积积分（连续信号）
  • 7.卷积和（离散信号）

在这里插入图片描述

1.信号具有时间特性和频率特性。

信号是时间的函数，因而表现出一定的时间特性，如出现的先后、持续时间的长短、随时间变化的快慢等；

信号也是频率的函数，因而也表现出一定的频率特性，如含有哪些频率成分、各频率分量的幅度及相位、信号的有效带宽等。

2.模拟转数字，抽样、量化、编码

答：
模拟信号变换为数字信号一般需要经过三个过程：抽样、量化、编码。其中，抽样和量化即是对模拟信号的时间轴取值和函数取值分别进行离散化。

3.阶跃信号和冲激信号

答：
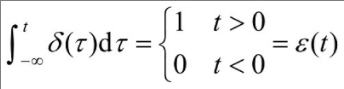
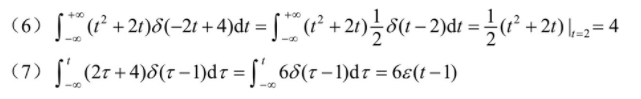
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

4.信号的波形变换（时移、折叠、尺度变换）

答：
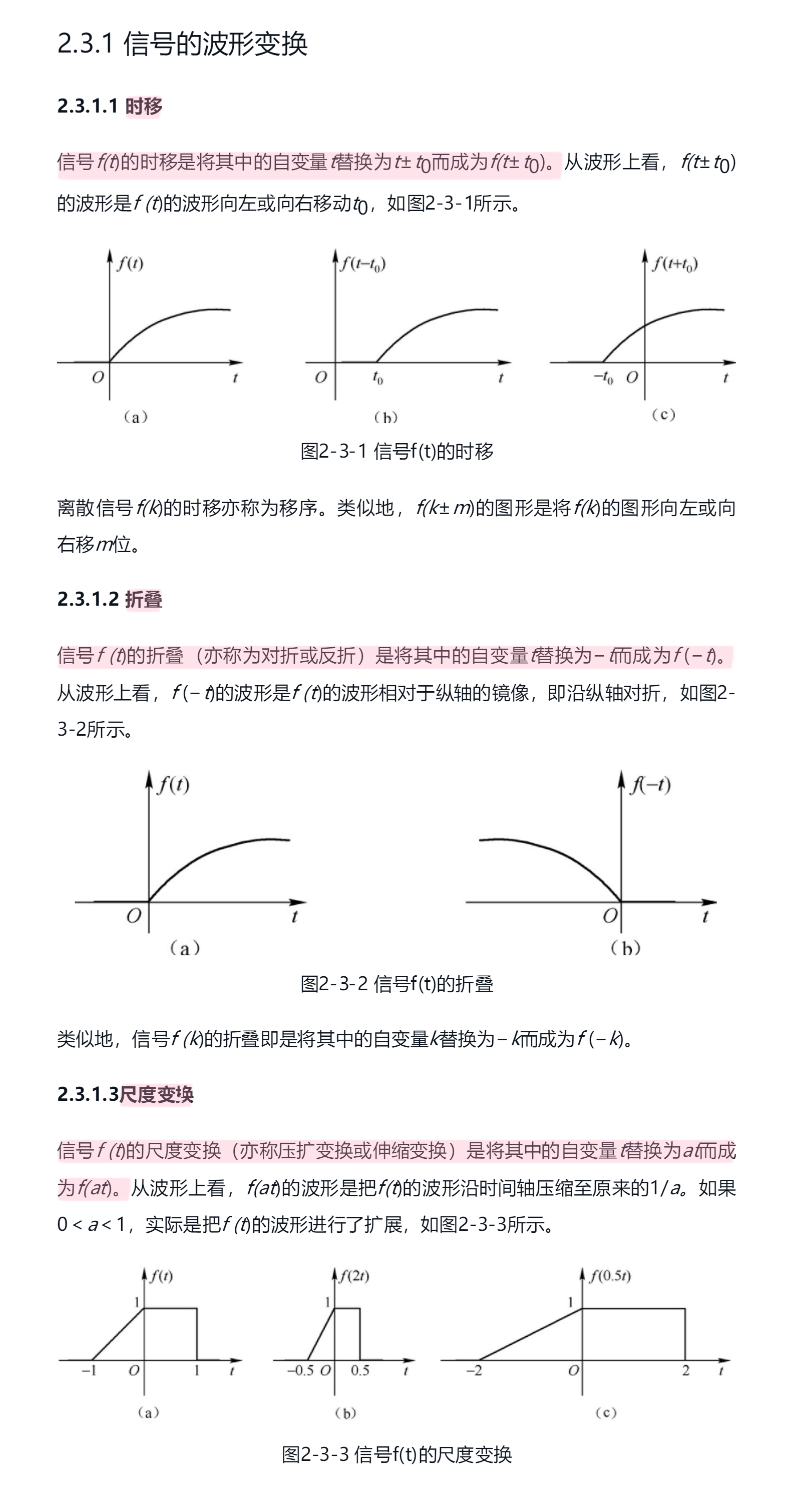
在这里插入图片描述

5.信号的基本运算（加减、相乘、微分与积分、差分与累加）

答：
两个信号相加（或相乘）后在某一时刻的值等于两个信号在此时刻的值相加（或相乘）。

5.1 相加减

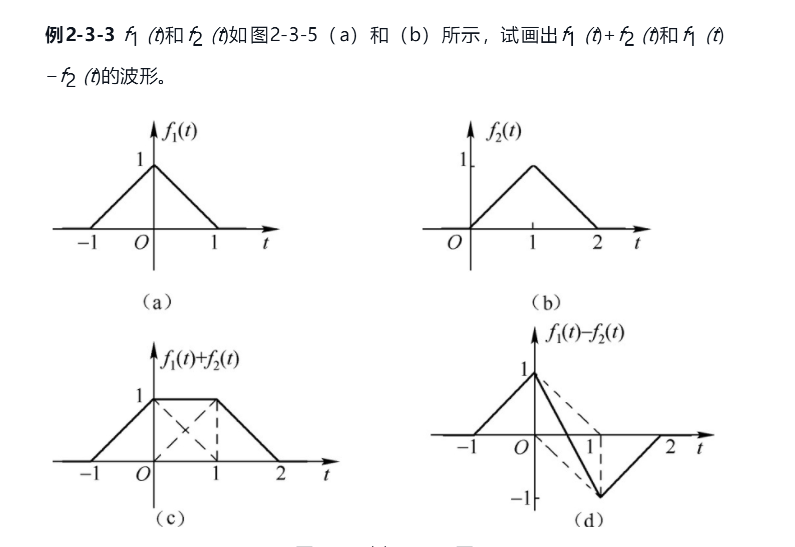
在这里插入图片描述

5.2 相乘

答：
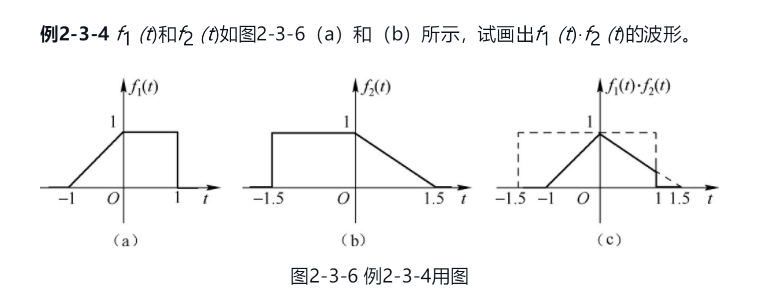
在这里插入图片描述

5.3 微分与积分

答：
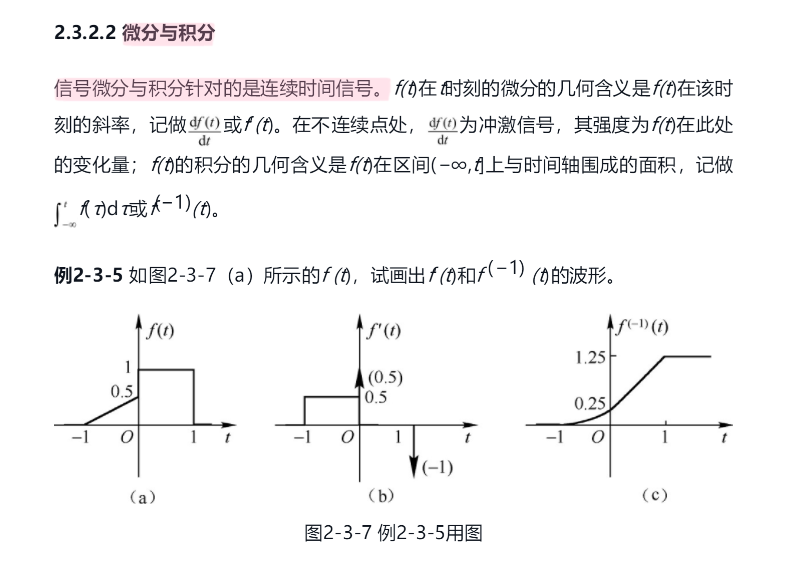
在这里插入图片描述

5.4 差分与累加

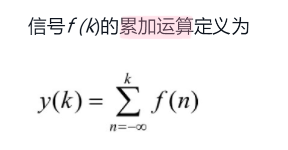
在这里插入图片描述
在这里插入图片描述

6.卷积积分（连续信号）

答：
在这里插入图片描述
在这里插入图片描述

7.卷积和（离散信号）

答：
在这里插入图片描述
在这里插入图片描述

相关文章：

电路学习+硬件每日学习十个知识点（40）23.8.20 （希腊字母读音，阶跃信号和冲激信号的关系式，信号的波形变换，信号的基本运算，卷积积分，卷积和）

文章目录 1.信号具有时间特性和频率特性。2.模拟转数字，抽样、量化、编码3.阶跃信号和冲激信号4.信号的波形变换（时移、折叠、尺度变换）5.信号的基本运算（加减、相乘、微分与积分、差分与累加）5.1 相加减5.2 相乘5.3 微…...

编程日记 2023/8/24 12:02:23

Python——列表(list)推导式

本文基于python3。 目录 1、Python推导式2、列表(list)推导式2.1、定义2.2、实际操作2.2.1、一个表达式，后面为一个 for 子句2.2.2、一个表达式，后面为一个 for 子句，然后，跟着if 子句。2.2.3、一个表达式，后面为一个…...

编程日记 2023/8/24 12:01:21

代码随想录算法训练营day43 | LeetCode 1049. 最后一块石头的重量 II 494. 目标和 474. 一和零

1049. 最后一块石头的重量 II（题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台） 思路：把全部石头重量加起来，然后除以二，就等于背包的最大容量。然后就可以按照背包问题…...

编程日记 2023/8/24 12:00:19

Linux安装jdk、mysql、并部署Springboot项目

😜作 者：是江迪呀✒️本文关键词：Linux、环境安装、JDK安装、MySQL、MySQL安装☀️每日 一言：知行合一！ 文章目录 一、前言二、安装步骤2.1 安装JDK（1）创建文件夹（便于后…...

编程日记 2023/8/24 11:59:18

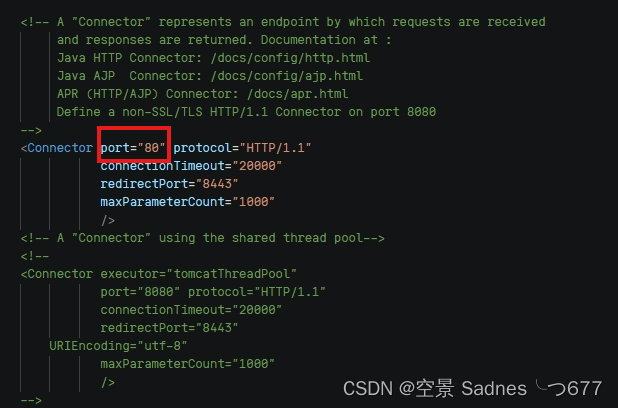
tomcat更改端口号和隐藏端口号

因为默认端口:8080不会自动隐藏，因此为了更显格调需要将其改为:80 进入tomcat的server文件 将其改为80，之后将tomcat重新启动即可 tomcat启动流程 [rootshang ~]# cd /usr/local/tomcat/apache-tomcat-8.5.92 [rootshang apache-tomcat-8.5.92]# cd b…...

编程日记 2023/8/24 11:58:16

生信分析Python实战练习 2 | 视频19

开源生信 Python教程 生信专用简明 Python 文字和视频教程 源码在：https://github.com/Tong-Chen/Bioinfo_course_python 目录 背景介绍 编程开篇为什么学习Python如何安装Python如何运行Python命令和脚本使用什么编辑器写Python脚本Python程序事例Python基本语法 数…...

编程日记 2023/8/24 11:57:15

wps设置其中几页为横版

问题：写文档的时候，有些表格列数太多，页面纵向显示内容不完整，可以给它改成横向显示。 将鼠标放在表格上一页的底部，点击‘插入-分页-下一页分节符’。 将鼠标放在表格页面的底部，点击‘插入-分页-下一页分…...

编程日记 2023/8/24 11:56:14

如何在Ubuntu 22.04上安装PHP 8.1并设置本地开发环境

引言 PHP是一种流行的服务器脚本语言，用于创建动态和交互式web页面。开始使用你选择的语言是学习编程的第一步。 本教程将指导您在Ubuntu上安装PHP 8.1，并通过命令行设置本地编程环境。您还将安装依赖管理器Composer，并通过运行脚本来测试您…...

编程日记 2023/8/24 11:55:13

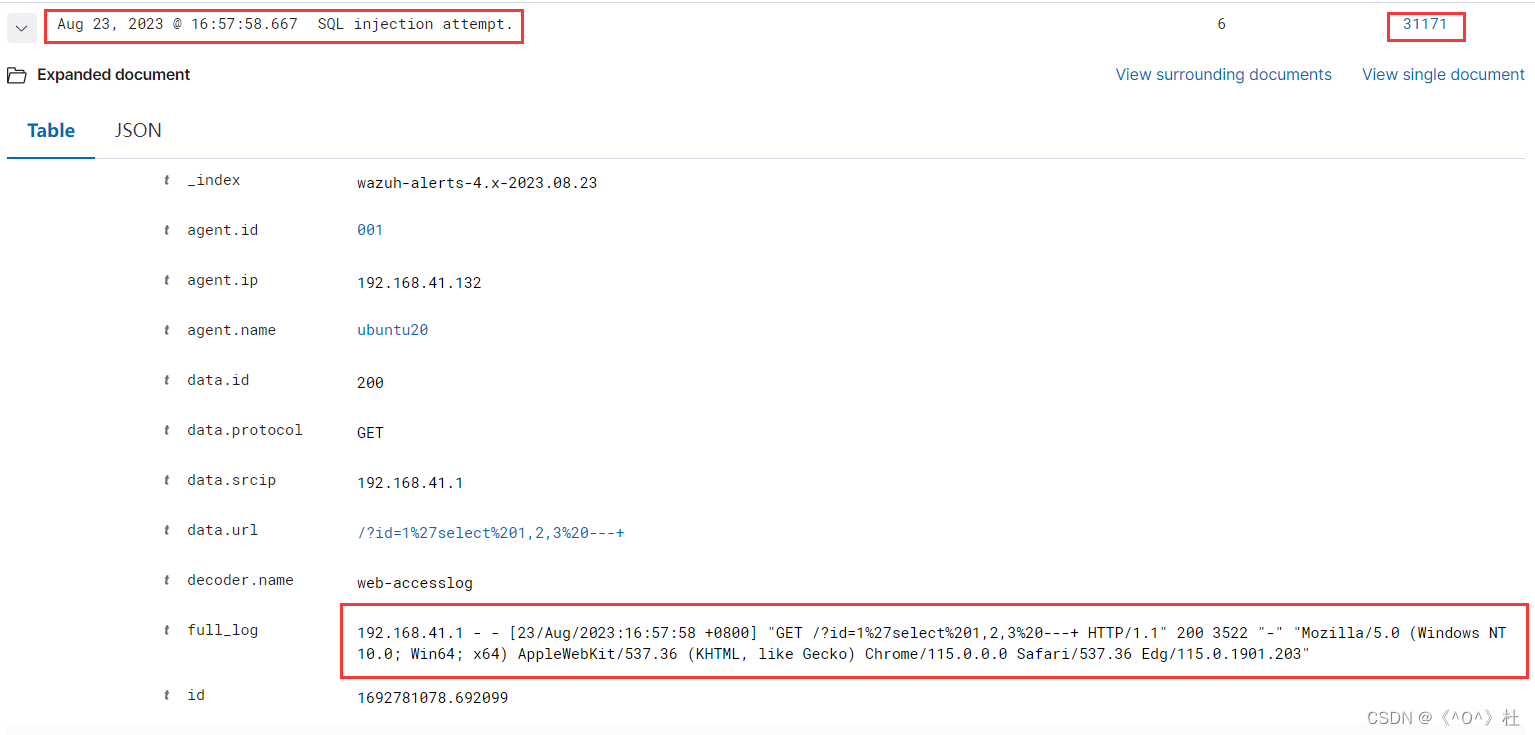
wazuh安装与使用

目录 一、wazuh安装 二、wazuh使用 一、wazuh安装 下载：https://wazuh.com 可以直接安装OVA这个，然后导入到Linux中就可以使用了。 导入完毕后开启，使用远程连接工具进行连接，出现以下画面则成功了。 之后可以看一下图形化界面…...

编程日记 2023/8/24 11:54:11

Vue 3 常见面试题汇总

前端面试题库 （面试必备） 推荐：★★★★★ 地址：前端面试题库 前言 最近两年许多大厂都在实行“降本增效”、“优化组织架构”，然后“为社会输送了大量人才”，今年（2023&#xff…...

编程日记 2023/8/24 11:53:10

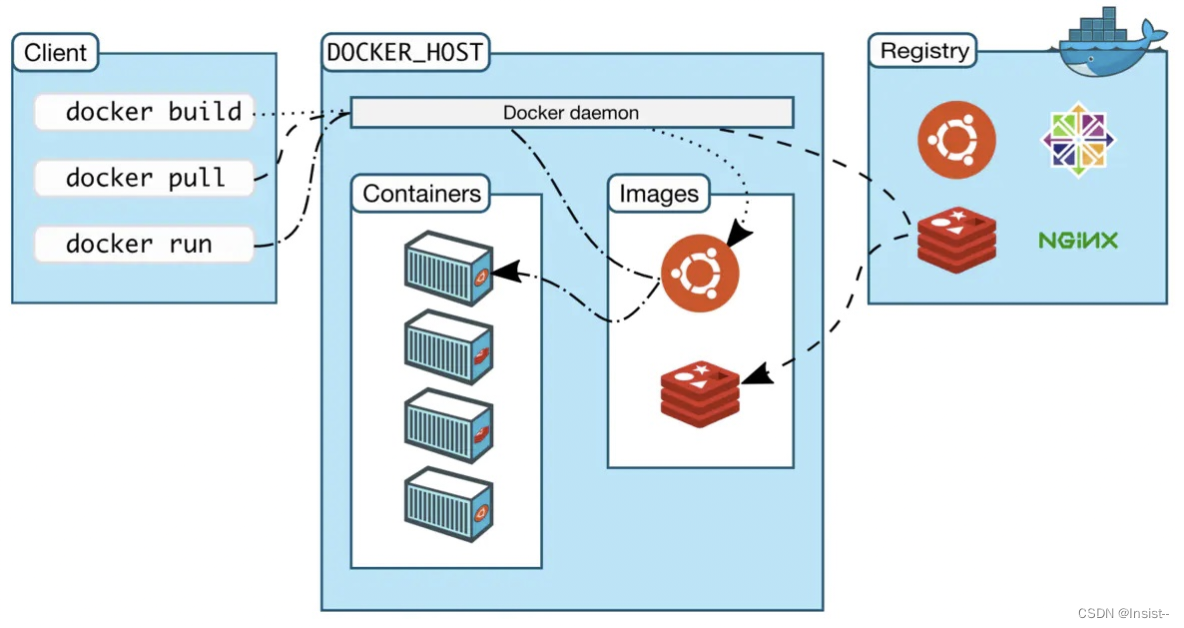
Docker是什么？详谈它的框架、使用场景、优势

作者：Insist-- 个人主页：insist--个人主页 作者会持续更新网络知识和python基础知识，期待你的关注 目录 一、什么是 Docker？ 二、Docker 的架构 1、Docker客户端 2、Docker守护进程 3、Docker镜像 4、Docker容器 5、Docker…...

编程日记 2023/8/24 11:52:09

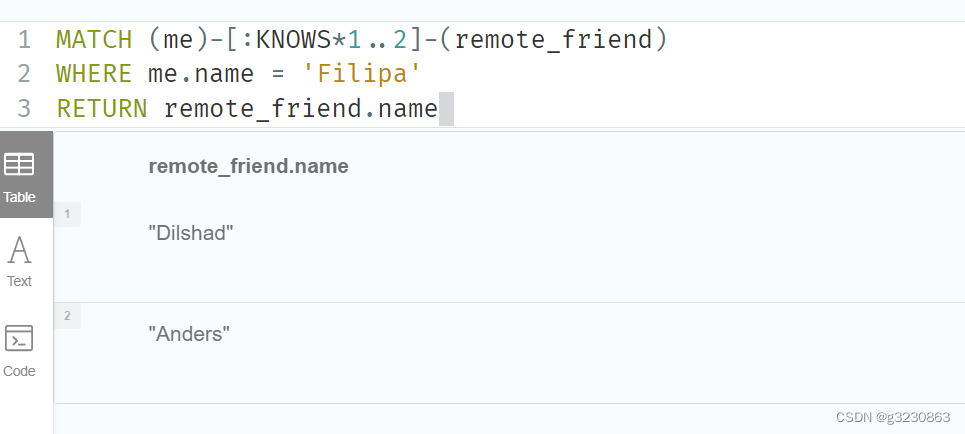
neo4j

UNWIND 将列表里的值展开 CREATE (N0:Person {name: Anders}) CREATE (N1:Person {name: Becky}) CREATE (N2:Person {name: Cesar}) CREATE (N3:Person {name: Dilshad}) CREATE (N4:Person {name: George}) CREATE (N5:Person {name: Filipa})CREATE (N0)-[:KNOWS]->(N3)…...

编程日记 2023/8/24 11:51:07

【项目 计网5】 4.15 TCP通信实现（服务器端）4.16 TCP通信实现（客户端）

文章目录 4.15 TCP通信实现&#xff08;服务器端&#xff09;4.16 TCP通信实现&#xff08;客户端&#xff09; 4.15 TCP通信实现&#xff08;服务器端&#xff09; // TCP 通信的服务器端// TCP 通信的服务器端 #include <stdio.h> #include <arpa/inet.h> #incl…...

编程日记 2023/8/24 11:50:06

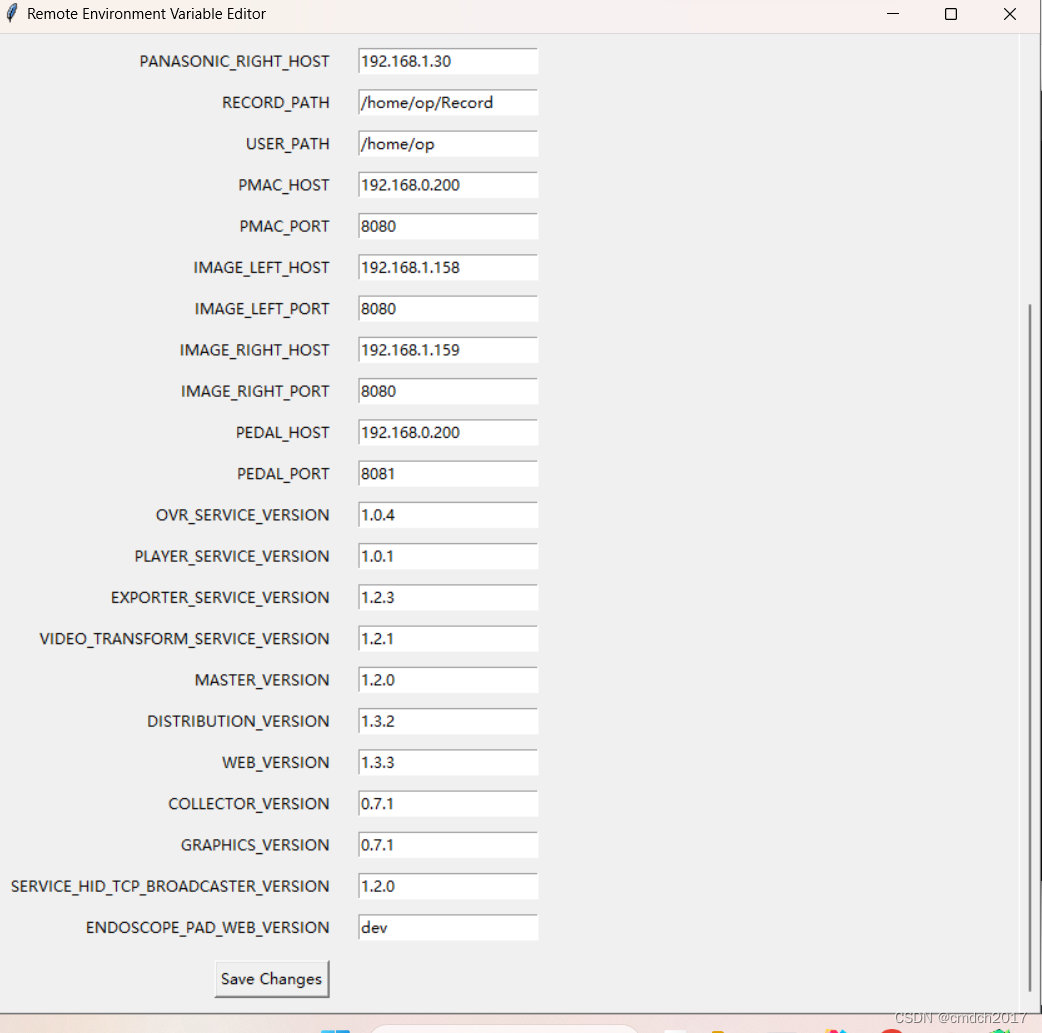
windows可视化界面管理服务器上的env文件

需求&#xff1a;在 Windows 环境中通过可视化界面编辑位于 Linux 主机上的 env 文件的情况&#xff0c;我现在环境是windows环境&#xff0c;我的env文件在linux的192.168.20.124上&#xff0c;用户是op&#xff0c;密码是op&#xff0c;文件绝对路径是/home/op/compose/env …...

编程日记 2023/8/24 11:49:04

自然语言处理在智能客服和聊天机器人中的应用

文章目录 1. 引言2. NLP基础2.1 词法分析2.2 语法分析2.3 语义理解2.4 情感分析 3. 智能客服中的应用3.1 自动问答3.2 意图识别3.3 情感分析与情绪识别 4. 聊天机器人中的应用4.1 对话生成4.2 上下文理解 5. 技术原理与挑战5.1 语言模型5.2 数据质量和多样性5.3 上下文理解 6. …...

编程日记 2023/8/24 11:48:01

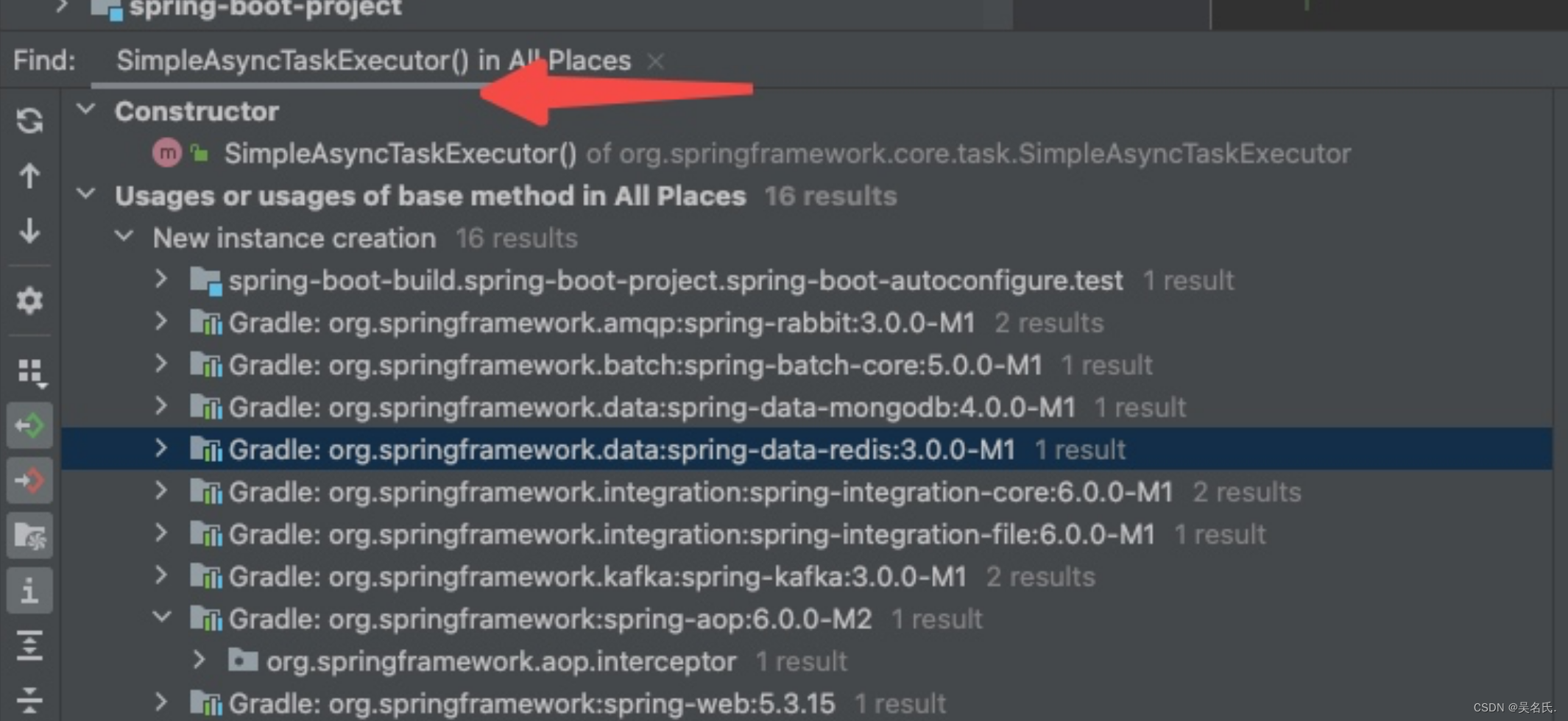
为什么不建议使用@Async注解创建线程

1 前言 在很久很久之前&#xff0c;我有一段痛苦的记忆。那种被故障所驱使的感觉&#xff0c;在我脑海里久久无法驱散。 原因无它&#xff0c;有小伙伴开启了线程池的暴力使用模式。没错&#xff0c;就是下面这篇文章。 夺命故障 ! 炸出了投资人&#xff01; 我有必要简单的…...

编程日记 2023/8/24 11:46:59

更新Ubuntu18.04上的CUDA和GCC

问题&#xff1a; 有一台服务器的GPU是1080&#xff0c;有八张卡&#xff0c;已经好久没有人用了。cuda版本是10.1,我现在拿来复现一些论文的模型&#xff0c;经常遇到版本依赖问题&#xff0c;报错Driver is too old。所以要更新一下驱动。遇到的主要问题是gcc版本也太低了&am…...

编程日记 2023/8/24 11:45:57

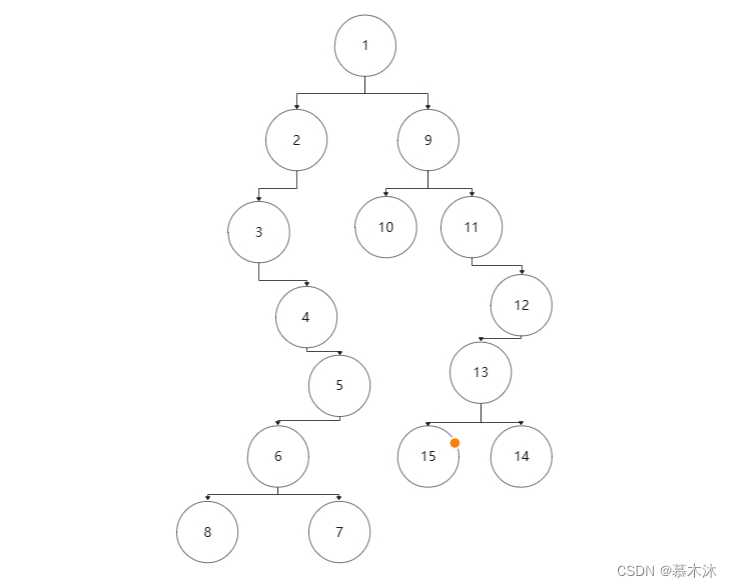
算法通过村第6关【青铜】| 如何通过中序和后序遍历恢复二叉树

中序&#xff1a;3 4 8 6 7 5 2 1 10 9 11 15 13 14 12 后序&#xff1a;8 7 6 5 4 3 2 10 15 14 13 12 11 9 1 通过这两个遍历顺序恢复二叉树 首先我们知道中序遍历顺序左中右&#xff0c;后序遍历顺序左右中 第一步&#xff1a; 由后序遍历确定根结点为1 > 由中序遍历…...

编程日记 2023/8/24 11:44:56

高斯牛顿法和LM算法异同示例

LM&#xff08;Levenberg-Marquardt&#xff09;算法和高斯牛顿&#xff08;Gauss-Newton&#xff09;算法是两种用于非线性最小二乘问题的优化算法&#xff0c;它们也有一些相似之处&#xff1a; 迭代优化&#xff1a;LM算法和高斯牛顿算法都使用迭代的方式来优化参数值&#…...

编程日记 2023/8/24 11:43:54

奥威BI财务数据分析方案：只做老板想看的

奥威BI财务数据分析方案是一套从老板的视角出发&#xff0c;做老板想看的财务数据分析报表&#xff0c;帮助老板更好地了解公司的财务状况和经营绩效的综合性智能财务数据分析方案&#xff0c;可实现财务数据分析可视化、灵活自主性&#xff0c;随时为老板提供最为直观的财务数…...

编程日记 2023/8/24 11:42:49

日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする

日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする 1、前言（1）情况说明（2）工程师的信仰2、知识点（1）　にする1，接续：名词＋にする2，接续：疑问词＋にする3，（A）は（B）にする。（2）復習：（1）复习句子（2）ために　＆　ように（３）そう（４）にする3、…...

编程新知 2025/11/20 7:52:01

STM32标准库-DMA直接存储器存取

文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA&#xff08;Direct Memory Access&#xff09;直接存储器存取 DMA可以提供外设…...

编程新知 2026/1/26 10:55:51

cf2117E

原题链接&#xff1a;https://codeforces.com/contest/2117/problem/E 题目背景&#xff1a; 给定两个数组a,b&#xff0c;可以执行多次以下操作&#xff1a;选择 i (1 < i < n - 1)&#xff0c;并设置 或&#xff0c;也可以在执行上述操作前执行一次删除任意 和 。求…...

编程新知 2026/2/4 15:29:40

uniapp微信小程序视频实时流+pc端预览方案

方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度​WebSocket图片帧​定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐​RTMP推流​TRTC/即构SDK推流❌ 付费方案 &#xff08;部分有免费额度&#x…...

编程新知 2026/1/31 6:12:33

Android15默认授权浮窗权限

我们经常有那种需求&#xff0c;客户需要定制的apk集成在ROM中&#xff0c;并且默认授予其【显示在其他应用的上层】权限&#xff0c;也就是我们常说的浮窗权限&#xff0c;那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

编程新知 2026/2/1 4:13:59

并发编程 - go版

1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程&#xff0c;系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

编程新知 2026/1/31 6:50:52

离线语音识别方案分析

随着人工智能技术的不断发展&#xff0c;语音识别技术也得到了广泛的应用&#xff0c;从智能家居到车载系统&#xff0c;语音识别正在改变我们与设备的交互方式。尤其是离线语音识别&#xff0c;由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力&#xff0c;广…...

编程新知 2025/9/22 13:00:25

6️⃣Go 语言中的哈希、加密与序列化：通往区块链世界的钥匙

Go 语言中的哈希、加密与序列化：通往区块链世界的钥匙 一、前言：离区块链还有多远？ 区块链听起来可能遥不可及，似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上，构建一个区块链的核心并不复杂，尤其当你已经掌握了一门系统编程语言，比如 Go。 要真正理解区…...

编程新知 2025/10/12 1:37:40

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter

java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用&#xff08;Math::max&#xff09; 2 函数接口…...

编程新知 2026/2/4 6:10:10

【1】跨越技术栈鸿沟：字节跳动开源TRAE AI编程IDE的实战体验

2024年初&#xff0c;人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目&#xff08;一款融合大型语言模型能力的云端AI编程IDE&#xff09;时&#xff0c;技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力&#xff0c;TRAE在WayToAGI等…...

编程新知 2026/1/31 20:18:53