机器学习笔记之谱聚类(一)k-Means聚类算法介绍
机器学习笔记之谱聚类——K-Means聚类算法介绍
引言
从本节开始,将介绍聚类任务,本节将介绍k-Means\text{k-Means}k-Means算法。
回顾:高斯混合模型
高斯混合模型(Gaussian Mixture Model,GMM\text{Gaussian Mixture Model,GMM}Gaussian Mixture Model,GMM)是一种处理聚类任务的常用模型。作为一种概率生成模型,它的概率图结构可表示为如下形式:
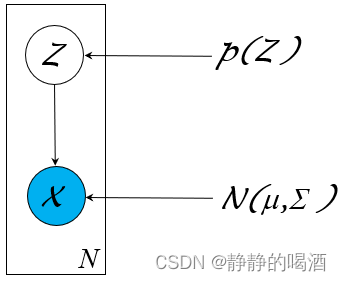
其中隐变量Z\mathcal ZZ是一个离散型随机变量,对应随机变量X\mathcal XX的后验结果服从高斯分布:
Z∼Categorical Distribution(1,2,⋯,K)X∣Z∼N(μk,Σk)k∈{1,2,⋯,K}\begin{aligned} \mathcal Z & \sim \text{Categorical Distribution}(1,2,\cdots,\mathcal K) \\ \mathcal X & \mid \mathcal Z \sim \mathcal N(\mu_{k},\Sigma_{k}) \quad k \in \{1,2,\cdots,\mathcal K\} \end{aligned}ZX∼Categorical Distribution(1,2,⋯,K)∣Z∼N(μk,Σk)k∈{1,2,⋯,K}
从生成模型的角度,高斯混合模型对P(X,Z)\mathcal P(\mathcal X,\mathcal Z)P(X,Z)进行建模。关于X\mathcal XX的概率密度函数P(X)\mathcal P(\mathcal X)P(X)可表示为如下形式:
其中PZk\mathcal P_{\mathcal Z_k}PZk表示隐变量Z\mathcal ZZ选择离散结果kkk时的概率结果;μZk,ΣZk\mu_{\mathcal Z_k},\Sigma_{\mathcal Z_k}μZk,ΣZk表示对应X∣Zk\mathcal X \mid \mathcal Z_kX∣Zk高斯分布的均值和协方差信息。
P(X)=∑ZP(X,Z)=∑ZP(Z)⋅P(X∣Z)=∑k=1KPZk⋅N(μZk,ΣZk)\begin{aligned} \mathcal P(\mathcal X) & = \sum_{\mathcal Z} \mathcal P(\mathcal X,\mathcal Z) \\ & = \sum_{\mathcal Z} \mathcal P(\mathcal Z) \cdot \mathcal P(\mathcal X \mid \mathcal Z) \\ & = \sum_{k=1}^{\mathcal K}\mathcal P_{\mathcal Z_k} \cdot \mathcal N(\mu_{\mathcal Z_k},\Sigma_{\mathcal Z_k}) \end{aligned}P(X)=Z∑P(X,Z)=Z∑P(Z)⋅P(X∣Z)=k=1∑KPZk⋅N(μZk,ΣZk)
聚类任务基本介绍
在生成模型综述——监督学习与无监督学习中简单介绍过,聚类(Clustering\text{Clustering}Clustering)任务属于无监督学习(Unsupervised Learning\text{Unsupervised Learning}Unsupervised Learning)任务。无监督学习任务的特点是:样本标签是未知的。而无监督学习的目标是通过学习无标签的样本来揭示数据的内在性质及规律。
而聚类试图将数据集内的样本划分为若干个子集,每个子集称为一个簇(Cluster\text{Cluster}Cluster)。从概率/非概率模型的角度划分,概率模型的典型模型是高斯混合模型;而非概率的聚类模型,其主要代表是 kkk均值算法(k-Means\text{k-Means}k-Means)。
距离计算
在介绍k-Means\text{k-Means}k-Means算法之前,需要介绍聚类的有效性指标(Vaildity Index\text{Vaildity Index}Vaildity Index)。从直观上描述,在聚类的过程我们更希望物以类聚——相同簇的样本尽可能地彼此相似,不同簇的样本尽可能地不同。
对于两个样本点,通常使用计算它们在样本空间中的距离 来描述两样本之间的相似性程度。样本之间距离越小,样本之间的相似性程度越高,反之同理。
已知两个样本x(i),x(j)x^{(i)},x^{(j)}x(i),x(j)表示如下:
它们均属于ppp维特征空间,即x(i),x(j)∈Rpx^{(i)},x^{(j)} \in \mathbb R^px(i),x(j)∈Rp.
{x(i)=(x1(i),x2(i),⋯,xp(i))Tx(j)=(x1(j),x2(j),⋯,xp(j))T\begin{cases} x^{(i)} = \left(x_1^{(i)},x_2^{(i)},\cdots,x_p^{(i)}\right)^T \\ x^{(j)} = \left(x_1^{(j)},x_2^{(j)},\cdots,x_p^{(j)}\right)^T \end{cases}⎩⎨⎧x(i)=(x1(i),x2(i),⋯,xp(i))Tx(j)=(x1(j),x2(j),⋯,xp(j))T
关于描述样本x(i),x(j)x^{(i)},x^{(j)}x(i),x(j)之间的距离,最常用的方法是明可夫斯基距离(Minkowski Distance\text{Minkowski Distance}Minkowski Distance):
其中参数m≥1m \geq 1m≥1.
Distmk(x(i),x(j))=(∑k=1p∣xk(i)−xk(j)∣m)1m\text{Dist}_{\text{mk}}(x^{(i)},x^{(j)}) = \left(\sum_{k=1}^p \left|x_k^{(i)} - x_k^{(j)}\right|^m\right)^{\frac{1}{m}}Distmk(x(i),x(j))=(k=1∑pxk(i)−xk(j)m)m1
当m=2m=2m=2时的明可夫斯基距离即欧几里得距离(Euclidean Distance\text{Euclidean Distance}Euclidean Distance),也称欧式距离:
Disted(x(i),x(j))=(∑k=1p∣xk(i)−xk(j)∣2)12=∑k=1p∣xk(i)−xk(j)∣2=∣∣x(i)−x(j)∣∣2\begin{aligned} \text{Dist}_{\text{ed}}(x^{(i)},x^{(j)}) & = \left(\sum_{k=1}^p \left|x_k^{(i)} - x_k^{(j)}\right|^2\right)^{\frac{1}{2}} \\ & = \sqrt{\sum_{k=1}^p \left|x_k^{(i)} - x_k^{(j)}\right|^2} \\ & = \left|\left|x^{(i)} - x^{(j)}\right|\right|_2 \end{aligned}Disted(x(i),x(j))=(k=1∑pxk(i)−xk(j)2)21=k=1∑pxk(i)−xk(j)2=x(i)−x(j)2
当m=1m=1m=1时的明可夫斯基距离即曼哈顿距离(Manhattan Distance\text{Manhattan Distance}Manhattan Distance):
Distman=∑k=1p∣xk(i)−xk(j)∣=∣∣x(i)−x(j)∣∣1\begin{aligned} \text{Dist}_{\text{man}} & = \sum_{k=1}^p \left|x_k^{(i)} - x_k^{(j)}\right| \\ & = \left|\left|x^{(i)} - x^{(j)}\right|\right|_1 \end{aligned}Distman=k=1∑pxk(i)−xk(j)=x(i)−x(j)1
k-Means\text{k-Means}k-Means算法介绍
给定一个样本集合D={x(1),x(2),⋯,x(N)}\mathcal D = \{x^{(1)},x^{(2)},\cdots,x^{(N)}\}D={x(1),x(2),⋯,x(N)},并设定簇的数量C={C1,C2,⋯,CK}\mathcal C = \{C_1,C_2,\cdots,C_{\mathcal K}\}C={C1,C2,⋯,CK},那么目标函数可描述成:对所有的簇,各簇内样本到均值向量之间的距离之和:
{E=∑k=1K∑x∈CkDist(x,μk)μk=1∣Ck∣∑x∈Ckx\begin{cases} \mathbb E = \sum_{k=1}^{\mathcal K} \sum_{x \in C_k} \text{Dist}(x,\mu_k) \\ \mu_{k} = \frac{1}{|C_k|} \sum_{x \in C_k} x \end{cases}{E=∑k=1K∑x∈CkDist(x,μk)μk=∣Ck∣1∑x∈Ckx
其中μk\mu_kμk表示簇CkC_kCk的均值向量。观察上式,∑x∈CkDist(x,μk)\sum_{x \in C_k} \text{Dist}(x,\mu_k)∑x∈CkDist(x,μk)描述了簇CkC_kCk内样本围绕μk\mu_kμk的紧密程度:
- 如果∑x∈CkDist(x,μk)\sum_{x \in C_k} \text{Dist}(x,\mu_k)∑x∈CkDist(x,μk)较小,那么簇CkC_kCk内样本的紧密程度就高;
- 同理,如果∑k=1K∑x∈CkDist(x,μk)\sum_{k=1}^{\mathcal K} \sum_{x \in C_k} \text{Dist}(x,\mu_k)∑k=1K∑x∈CkDist(x,μk)小,意味着各个簇内样本的紧密程度都较高,从而达到样本分类的目的。
如果想要通过这种方式去寻找各簇对应的μk\mu_kμk,这明显是一个NP-Hard\text{NP-Hard}NP-Hard问题:均值向量μk\mu_kμk并不是某个真实的样本点,因而它有无穷多种可能;虽然在给定样本的条件下,各簇对应的μk\mu_kμk是客观存在的,但相应寻找的代价是极高的。
假设在当前样本条件下,找到了最优的簇对应的μk\mu_kμk,但样本自身是存在噪声的,如果新加入样本进来,可能会使μk\mu_kμk产生变化。
那么k-Means\text{k-Means}k-Means方法采用贪心策略,通过迭代的方式去近似求解E=∑k=1K∑x∈CkDist(x,μk)\mathbb E = \sum_{k=1}^{\mathcal K} \sum_{x \in C_k} \text{Dist}(x,\mu_k)E=∑k=1K∑x∈CkDist(x,μk)的最小值。下面通过实例使用k-Means\text{k-Means}k-Means算法进行近似求解。
示例转载自K-means 算法【基本概念篇】非常感谢,侵删。
k-Means\text{k-Means}k-Means算法示例
已知包含二维特征的数据集合D\mathcal DD表示如下,并针对该集合使用k-Means\text{k-Means}k-Means算法执行聚类任务:
D={(2,10),(2,5),(8,4),(5,8),(7,5),(6,4),(1,2),(4,9)}\mathcal D = \{(2,10),(2,5),(8,4),(5,8),(7,5),(6,4),(1,2),(4,9)\}D={(2,10),(2,5),(8,4),(5,8),(7,5),(6,4),(1,2),(4,9)}
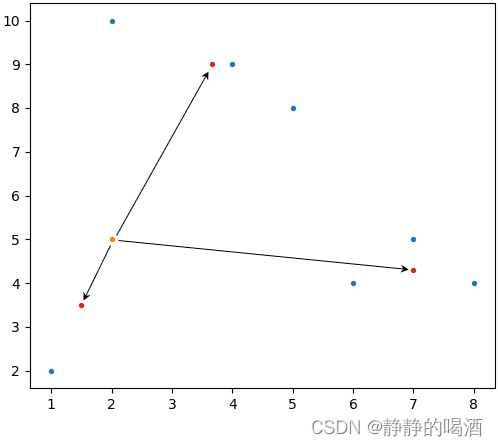
对应二维图像表示如下:
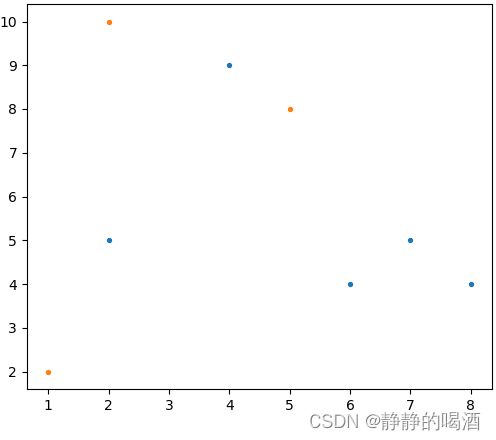
- 假设将上述集合内的样本点划分成三类,因此需要选择三个类对应的初始中心。这里我们从集合中随机选择样本点作为初始中心(上图中的橙色样本点):
当然,并不是说‘初始中心’就必须在样本中进行选择,实际上只要是样本空间中任意点都可作为初始中心。
μ1(init)=(2,10)μ2(init)=(5,8)μ3(init)=(1,2)\mu_1^{(init)} = (2,10)\quad \mu_2^{(init)} = (5,8)\quad \mu_3^{(init)} = (1,2)μ1(init)=(2,10)μ2(init)=(5,8)μ3(init)=(1,2) - 对两样本点之间的距离Dist(x(i),x(j));x(i),x(j)∈D\text{Dist}(x^{(i)},x^{(j)});x^{(i)},x^{(j)} \in \mathcal DDist(x(i),x(j));x(i),x(j)∈D进行定义。由于样本比较简单,这里直接定义为曼哈顿距离:
ρ[x(i),x(j)]=∣x1(i)−x1(j)∣+∣x2(i)−x2(j)∣{x(i)=(x1(i),x2(i))Tx(j)=(x1(j),x2(j))T\rho[x^{(i)},x^{(j)}] = \left|x_1^{(i)} - x_1^{(j)}\right| + \left|x_2^{(i)} - x_2^{(j)}\right| \quad \begin{cases} x^{(i)} = (x_1^{(i)},x_2^{(i)})^T \\ x^{(j)} = (x_1^{(j)},x_2^{(j)})^T \end{cases}ρ[x(i),x(j)]=x1(i)−x1(j)+x2(i)−x2(j){x(i)=(x1(i),x2(i))Tx(j)=(x1(j),x2(j))T - 定义完毕后,将所有样本点分别与三个初始中心计算曼哈顿距离。具体结果表示如下:
示例:样本点(5,8)(5,8)(5,8)与初始中心(2,10)(2,10)(2,10)之间的曼哈顿距离
ρ=∣5−2∣+∣8−10∣=5\rho = |5-2| + |8 - 10| = 5ρ=∣5−2∣+∣8−10∣=5
选择距离最小的初始中心,并划分至该初始中心对应的簇。
| SamplePoint/InitialCenter\text{SamplePoint/InitialCenter}SamplePoint/InitialCenter | μ1(init):(2,10)\mu_1^{(init)}:(2,10)μ1(init):(2,10) | μ2(init):(5,8)\mu_2^{(init)}:(5,8)μ2(init):(5,8) | μ3(init):(1,2)\mu_3^{(init)}:(1,2)μ3(init):(1,2) | ClusterResult\text{ClusterResult}ClusterResult |
|---|---|---|---|---|
| (2,10)(2,10)(2,10) | 000 | 555 | 999 | 111 |
| (2,5)(2,5)(2,5) | 555 | 666 | 444 | 333 |
| (8,4)(8,4)(8,4) | 121212 | 777 | 999 | 222 |
| (5,8)(5,8)(5,8) | 555 | 000 | 101010 | 222 |
| (7,5)(7,5)(7,5) | 101010 | 555 | 999 | 222 |
| (6,4)(6,4)(6,4) | 101010 | 555 | 777 | 222 |
| (1,2)(1,2)(1,2) | 999 | 101010 | 000 | 333 |
| (4,9)(4,9)(4,9) | 333 | 222 | 101010 | 222 |
至此,得到了第一次迭代产生的聚类结果表示如下:
{Cluster 1: (2,10)Cluster 2: (8,4),(5,8),(7,5),(6,4),(4,9)Cluster 3: (2,5),(1,2)\begin{cases} \text{Cluster 1: }(2,10) \\ \text{Cluster 2: }(8,4),(5,8),(7,5),(6,4),(4,9) \\ \text{Cluster 3: }(2,5),(1,2) \\ \end{cases}⎩⎨⎧Cluster 1: (2,10)Cluster 2: (8,4),(5,8),(7,5),(6,4),(4,9)Cluster 3: (2,5),(1,2)
-
基于第一次迭代,重新计算每个聚类的中心,并替换初始中心:
- Cluster 1: \text{Cluster 1: }Cluster 1: 本次聚类中,该类样本点只有1个,因而新的聚类中心就是它自身;
- Cluster 2: (6,6)⇐{xˉ1=(4+5+6+7+8)/5=6xˉ2=(4+4+5+8+9)/5=6\text{Cluster 2: } (6,6) \Leftarrow \begin{cases} \bar x_1 = (4+5+6+7+8) / 5 = 6 \\ \bar x_2 = (4+4+5+8+9) / 5 = 6\end{cases}Cluster 2: (6,6)⇐{xˉ1=(4+5+6+7+8)/5=6xˉ2=(4+4+5+8+9)/5=6
- Cluster 3: (1.5,3.5)⇐{(2+1)/2=1.5(5+2)/2=3.5\text{Cluster 3: }(1.5,3.5) \Leftarrow \begin{cases} (2 + 1)/2 = 1.5 \\ (5 + 2)/2 = 3.5 \end{cases}Cluster 3: (1.5,3.5)⇐{(2+1)/2=1.5(5+2)/2=3.5
此时,基于替换中心的样本空间以及聚类区域表示如下(红色样本点表示第一次迭代后的新聚类中心):
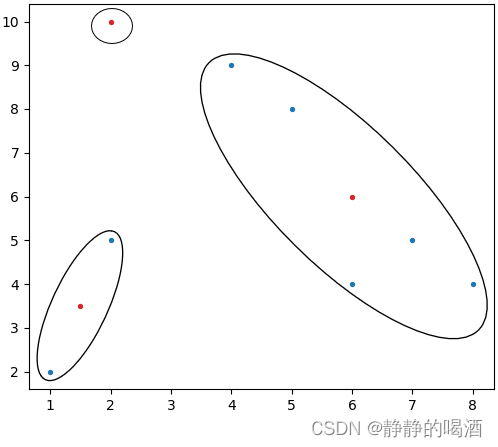
-
重复执行上述步骤,可以得到新的聚类中心以及对应的簇。直到聚类中心不再发生变化,这意味着:在迭代过程中,通过计算聚类中心所产生的簇内部的样本点已经稳定,不再发生变化。此时即可停止算法:
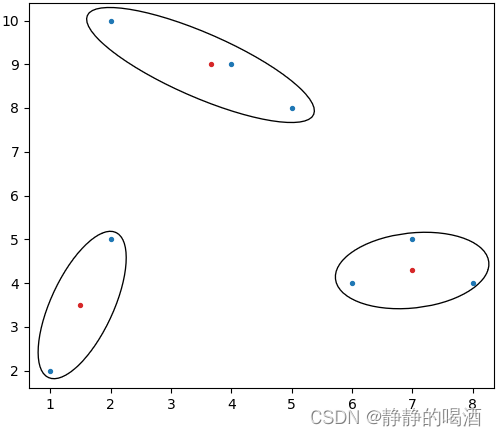
k-Means\text{k-Means}k-Means算法与高斯混合模型的关系
从上面的迭代过程中,可以发现:整个计算过程与概率没有明显的关联关系。我们仅仅在迭代过程中执行了计算距离并比较大小、更新聚类中心这两种操作。
但从单个样本点的角度,可以将其视作高斯混合模型的一种描述。以样本点(2,5)(2,5)(2,5)为例,对该样本到各聚类中心之间的距离进行计算,并将其映射至(0,1)区间:
注意:这里的箭头表示的是‘欧式距离’,而不是曼哈顿距离。这里仅表示一个指向,不要被误导。
注意:距离数值越小的,映射的结果越大。这意味着样本点与该聚类中心对应的簇关联更加密切。因而这里使用的标准化方法表示如下。其中NNN表示簇的个数;SumDistance\text{SumDistance}SumDistance表示样本到所有聚类中心的ManhattanDistance\text{ManhattanDistance}ManhattanDistance之和。
MappingResult=1N−1(1−ManhattanDistanceSumDistance)\text{MappingResult} = \frac{1}{N - 1}(1 - \frac{\text{ManhattanDistance}}{\text{SumDistance}})MappingResult=N−11(1−SumDistanceManhattanDistance)
这里的标准化方法仅仅描述映射后的大小关系,严格来说并不准确。这里提出一种函数Softmax(1ManhanttanDistance)\text{Softmax}(\frac{1}{\text{ManhanttanDistance}})Softmax(ManhanttanDistance1)作为参考。
| ManhattanDistance\text{ManhattanDistance}ManhattanDistance | MappingResult\text{MappingResult}MappingResult | |
|---|---|---|
| (1.5,3.5)(1.5,3.5)(1.5,3.5) | 222 | 0.42530.42530.4253 |
| (7,4.3)(7,4.3)(7,4.3) | 5.75.75.7 | 0.28680.28680.2868 |
| (3.67,9)(3.67,9)(3.67,9) | 5.675.675.67 | 0.28790.28790.2879 |
观察上述表格的MappingResult\text{MappingResult}MappingResult,完全可以将这一组数值P(Z)=[0.4253,0.5868,0.2879]\mathcal P(\mathcal Z) = [0.4253,0.5868,0.2879]P(Z)=[0.4253,0.5868,0.2879]看作是一个概率分布。该概率分布中概率值最大的是对应聚类中心(1.5,3.5)(1.5,3.5)(1.5,3.5)对应的簇结果。
另一种思路在于:此时的聚类中心已经不是样本点了,此时的聚类中心在样本空间中已经没有任何实际意义,也符合隐变量的描述。
而样本点在给定聚类中心Z\mathcal ZZ的条件下,那么样本点x(i)∣Zx^{(i)} \mid \mathcal Zx(i)∣Z服从高斯分布。因为该样本点距离聚类中心越近,意味着它从该簇中生成的概率越高。因而可将k-Means\text{k-Means}k-Means视作一种基于高斯混合模型思想的硬划分模型(Hard-GMM\text{Hard-GMM}Hard-GMM)。
k-Means\text{k-Means}k-Means算法的缺陷
虽然k-Means\text{k-Means}k-Means算法简单,但它同样存在缺陷:
- 我们需要手动添加聚类数量。这需要对样本信息有一定程度的了解,聚类数量的选择对聚类结果的影响是巨大的;
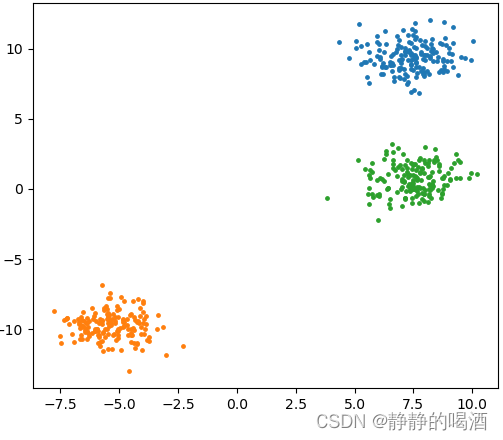
- 它对于聚类分布紧密(Compactness\text{Compactness}Compactness)的样本集合有不错的聚类效果,如簇是凸形状(Convex\text{Convex}Convex)这种类似云团状的分布结构:
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import clustern_samples = 500
colors = ["tab:blue","tab:orange","tab:green"]
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)X,y = blobs
KMeans = cluster.MiniBatchKMeans(n_clusters=3)
KMeans.fit(X)
yPred = KMeans.predict(X)for _,(XElement,yPredElement) in enumerate(zip(X,yPred)):plt.scatter(XElement[0],XElement[1],color=colors[yPredElement],s=5)
plt.show()返回结果如下:
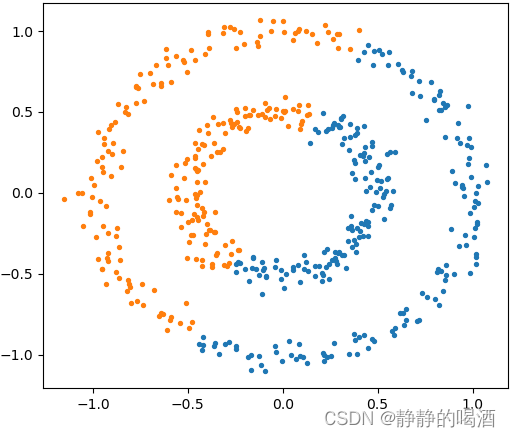
但针对连通性(Connectivity\text{Connectivity}Connectivity)簇分布,它的聚类结果可能并不漂亮:
我们原本希望将大圆与小圆中的样本划分开来;不仅k-Means出现这样的现象,高斯混合模型同样会出现这种现象。
blobs = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
关于这种结构,在核方法思想与核函数介绍中提到过,使用核方法 + k-Means\text{k-Means}k-Means的方式进行处理,但这种方式同样因维度增加而可能出现维度诅咒/维度惩罚(Curse of Dimensionary\text{Curse of Dimensionary}Curse of Dimensionary)的风险。因此,针对类似连通类型的簇分布,k-Means\text{k-Means}k-Means并不可取。
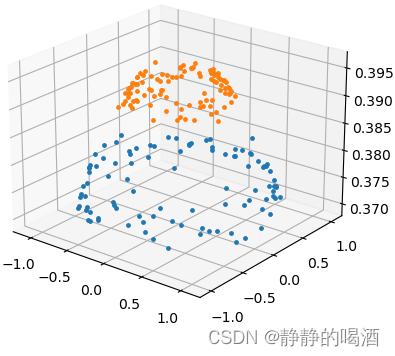
下一节从k-Means\text{k-Means}k-Means的缺陷开始,介绍谱聚类(Spectral Clusting\text{Spectral Clusting}Spectral Clusting)。
相关参考:
机器学习-谱聚类(1)-背景介绍
K-means 算法【基本概念篇】
Sklearn\text{Sklearn}Sklearn中文文档——K-means
机器学习——周志华著
相关文章:

机器学习笔记之谱聚类(一)k-Means聚类算法介绍
机器学习笔记之谱聚类——K-Means聚类算法介绍引言回顾:高斯混合模型聚类任务基本介绍距离计算k-Means\text{k-Means}k-Means算法介绍k-Means\text{k-Means}k-Means算法示例k-Means\text{k-Means}k-Means算法与高斯混合模型的关系k-Means\text{k-Means}k-Means算法的…...
云原生周刊 | 2023 年热门:云 IDE、Web Assembly 和 SBOM | 2023-02-20
在 CloudNative SecurityCon 上,云原生计算基金会的首席技术官 Chris Aniszczyk 在 The New Stack Makers 播客的这一集中强调了 2023 年正在形成几个趋势: 随着 GitHub 的 Codespaces 平台通过集成到 GitHub 服务中获得认可,云 IDE…...
python 打包EXE
注: 从个人博客园 移植而来 环境: Windows7 Python 2.7 参考: 使用pyinstaller打包python程序 Pyinstaller 打包发布经验总结 Using PyInstaller 简介 使用python引用第三方的各种模块编写一个工具后,如果想发给其他人&…...

CANopen概念总结、心得体会
NMT网络管理报文: NMT 主机和 NMT 从机之间通讯的报文就称为 NMT 网络管理报文。常见报文说明: 0101---------------网络报文发送Nmt_Start_Node,让电机进入OP模式(此时还不会发送同步信号) setState(d, Operational)------------------开启…...
【2】MYSQL数据的导入与导出
文章目录 MYSQL-库(相同库名称)的导入导出MYSQL-库(不同库名称)的导入导出MYSQL-表的导入导出MYSQL-表的指定查询记录导入导出前提: 客户端工具是:SQLyog MYSQL-库(相同库名称)的导入导出 1、选中指定库——右键,选择【将数据库复制到不同的主机/数据库】 2、选中指…...
Kaggle系列之CIFAR-10图像识别分类(残差网络模型ResNet-18)
CIFAR-10数据集在计算机视觉领域是一个很重要的数据集,很有必要去熟悉它,我们来到Kaggle站点,进入到比赛页面:https://www.kaggle.com/competitions/cifar-10CIFAR-10是8000万小图像数据集的一个子集,由60000张32x32彩…...
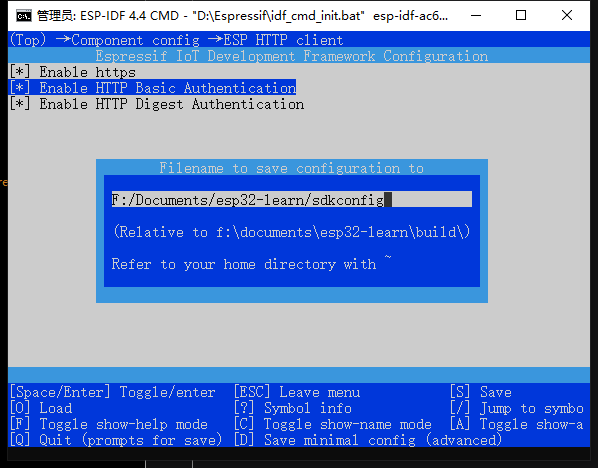
ESP-C3入门11. 创建最基本的HTTP请求
ESP-C3入门11. 创建最基本的HTTP请求一、menuconfig配置二、配置 CMakeLists1. 设置项目的额外组件目录2. 设置头文件搜索目录三、在 ESP32 上执行 HTTP 请求的基本步骤1. 创建 TCP 连接2. 设置 HTTP 请求3. 发送 HTTP 请求4. 接收 HTTP 响应5. 处理 HTTP 响应6. 关闭 TCP 连接…...
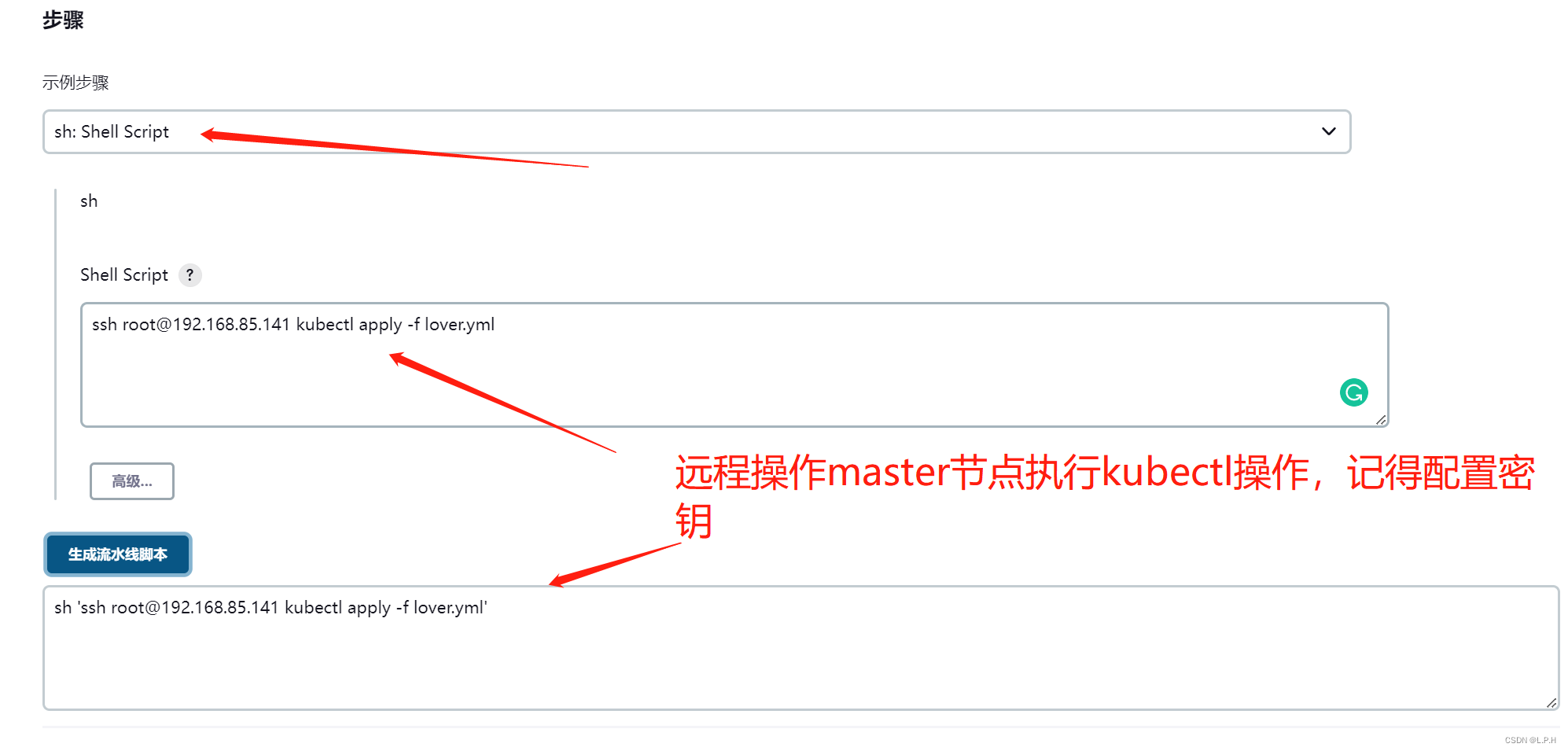
K8S+Jenkins+Harbor+Docker+gitlab集群部署
K8SJenkinsHarborDockergitlab服务器集群部署 目录K8SJenkinsHarborDockergitlab服务器集群部署1.准备以下服务器2.所有服务器统一处理执行2.1 关闭防火墙2.2 关闭selinux2.3 关闭swap(k8s禁止虚拟内存以提高性能)2.4 更新yum (看需要更新)2.5 时间同步2…...

看见统计——第四章 统计推断:频率学派
看见统计——第四章 统计推断:频率学派 接下来三节的主题是中心极限定理的应用。在不了解随机变量序列 {Xi}\{X_i\}{Xi} 的潜在分布的情况下,对于大样本量,中心极限定理给出了关于样本均值的声明。例如,如果 YYY 是一个 N(0&am…...
2023年2月访问学者博士后热门国家出入境政策变化汇总
近期关于出国的咨询量日益增多,出入境政策也是其中之一。所以本期知识人网小编汇总了最新访问学者和博士后关注的热门国家及地区入境政策变化,提供给大家。目前各国入境政策大致分为三种:一、 无法入境的国家如:摩洛哥、朝鲜等。二…...

“离开浪浪山”是假象,80%年轻人下班后还在学习,真实是想先上个山。
最近,又有一个关于年轻人与职场的新词横空出世—— 浪浪山。 什么是浪浪山? 每个人心中都有一座浪浪山。 浪浪山,其实是人生的一种状态,步入社会时满腔热血,然而很快就被现实给修理了一顿;想要辞职不干出去…...

Kotlin 33. CompileSdkVersion 和 targetSdkVersion 有什么区别?
CompileSdkVersion 和 targetSdkVersion 有什么区别? 在 build.gradle (Module) 文件中,我们通常会看到 CompileSdkVersion 和 targetSdkVersion 的使用,比如下面是一个完整的 build.gradle (Module) 文件: plugins {id com.and…...

实用调试技巧——“C”
各位CSDN的uu们你们好呀,今天小雅兰的内容是实用调试技巧,其实小雅兰一开始,也不知道调试到底是什么,一遇到问题,首先就是观察程序,改改这里改改那里,最后导致bug越修越多,或者是问别…...
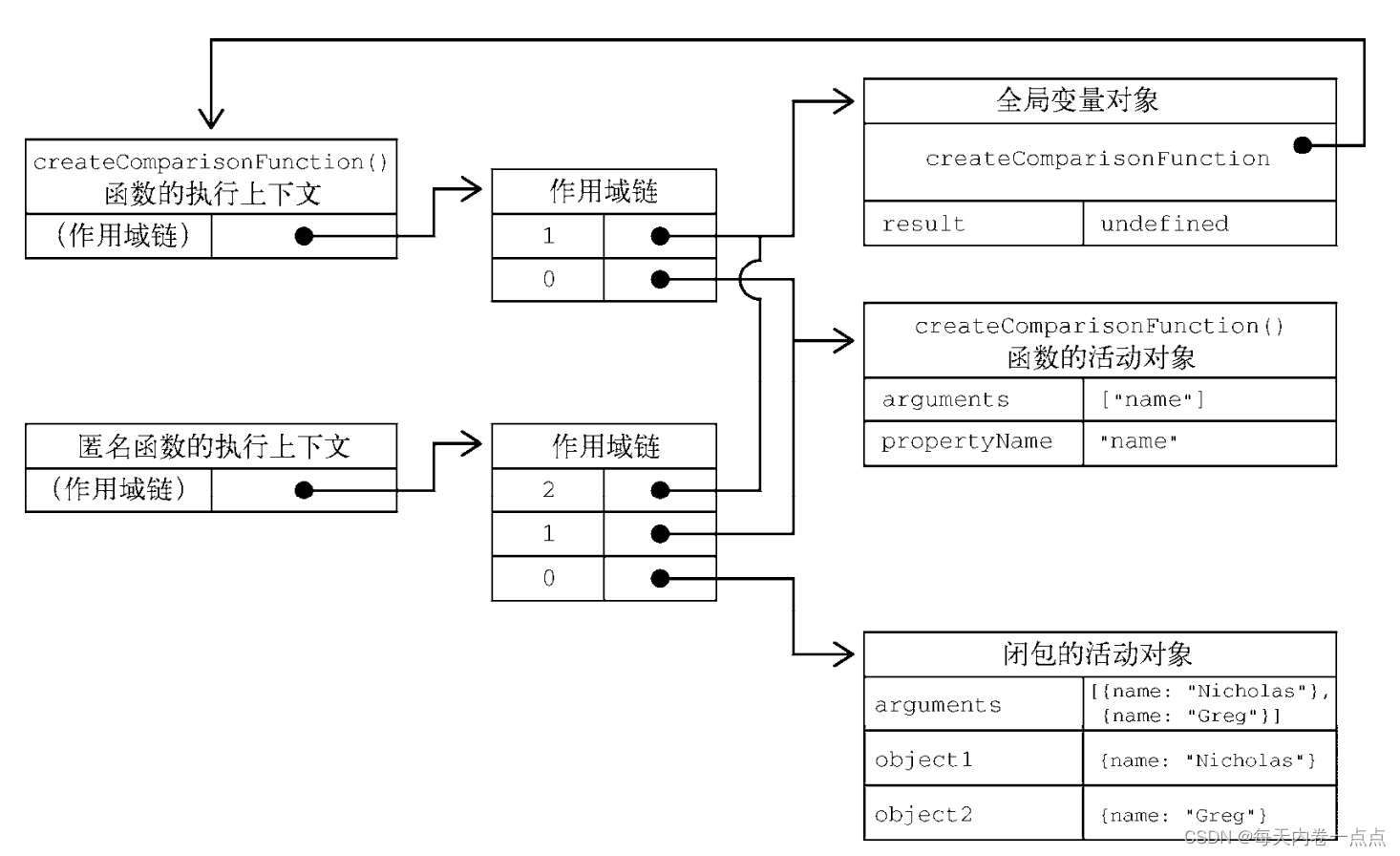
JavaScript - 函数
文章目录一、箭头函数二、函数名三、理解参数3.1 箭头函数中的参数四、没有重载五、默认参数值5.1 默认参数作用域与暂时性死区六、参数扩展与收集6.1 扩展参数6.2 收集参数七、函数声明与函数表达式八、函数作为值九、函数内部9.1 arguments9.2 this9.3 caller9.4 new.target十…...
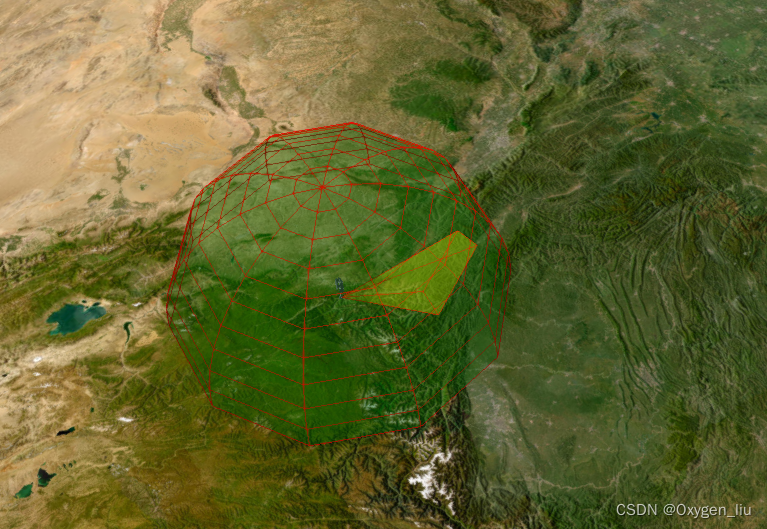
Cesium 卫星轨迹、卫星通信、卫星过境,模拟数据传输。
起因:看了cesium官网卫星通信示例发现只有cmzl版本的,决定自己动手写一个。欢迎大家一起探讨,评论留言。 效果 全部代码在最后 起步 寻找卫星轨迹数据,在网站space-track上找的,自己注册账号QQ邮箱即可。 卫星轨道类…...

2023年湖北中级职称(工程类建筑类)报名条件和要求是什么?
2023年湖北中级职称(工程类建筑类)报名条件和要求是什么? 中级职称分为计算机类、医药类、卫生类、教师类、工程类、经济类等各大类,今天主要就是跟大家说一下工程类中级职称评审的一个条件和要求,这也是评职称人员应该…...

socket编程复习
再次用到socket编程,将socket相关的知识点做了简单整理,根据网络上大家的整理,又做了一些调整和汇总。 API列表 sokect常见的API大致有列表里面这么多,不同平台的实现可能有些微的差别,下面对常用API的参数和用法做了…...
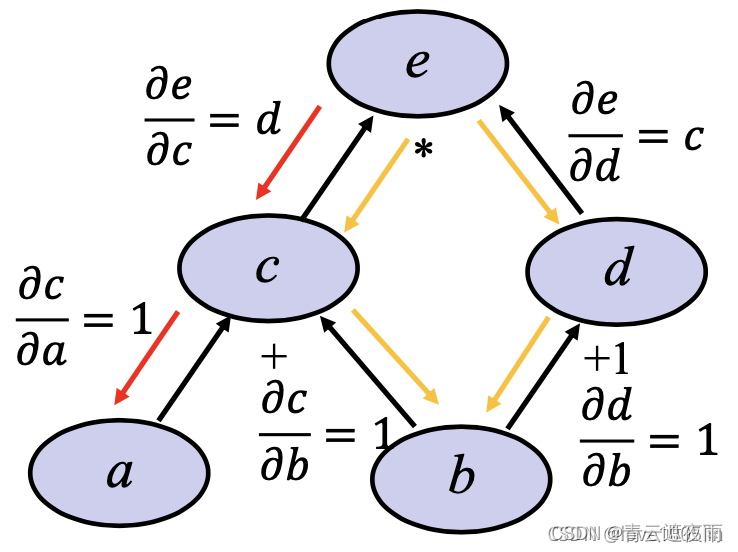
深度学习神经网络基础知识(三)前向传播,反向传播和计算图
专栏:神经网络复现目录 深度学习神经网络基础知识(三) 本文讲述神经网络基础知识,具体细节讲述前向传播,反向传播和计算图,同时讲解神经网络优化方法:权重衰减,Dropout等方法,最后进行Kaggle实…...
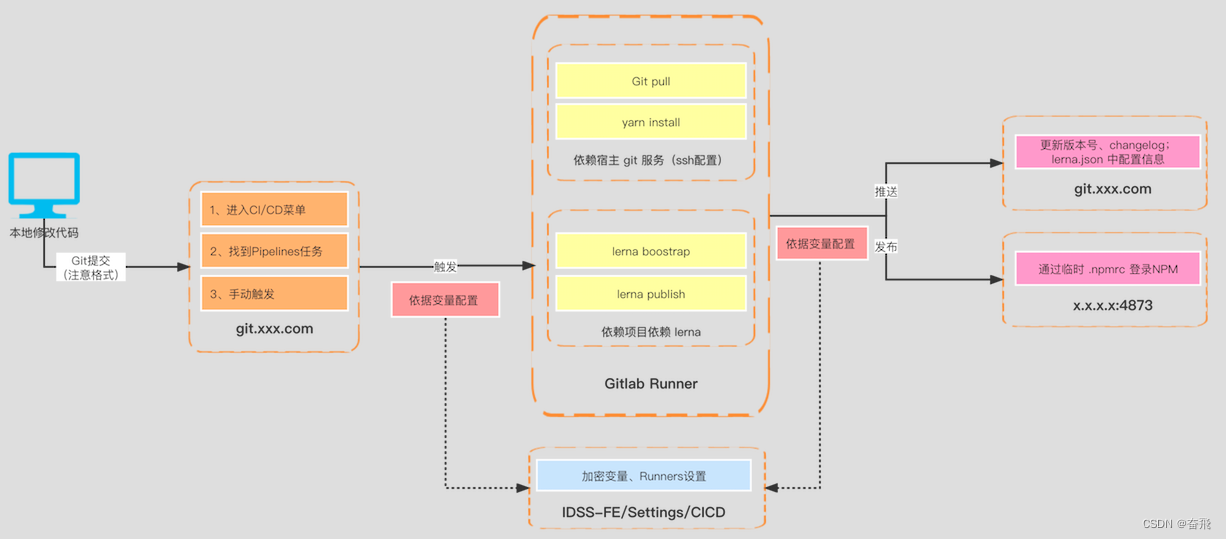
一图说明 monorepo 落地流程方案
关于 monorepo 初次讨论已有2年载,目前团队已经沉淀了成熟的技术方案且经受住了实战考验。所以特梳理相关如下: 也算是关于之前发起的 monorepo–依赖 的解答篇。 上图为目前团队贡献的主流程:① 本地开发 > ② 提交Git仓库 > ③ 触发…...

SAP ABAP WRITE语法大全
列表是ABAP/4报表程序数据的输出媒介。每个ABAP/4报表程序将其输出数据传递到直接与该程序连接的列表中。每个程序最多生成21个列表:1个基本列表和20个辅助列表。 将数据写入列表的基本ABAP/4语句是WRITE、SKIP和ULINE输出语句。 一、标准列表结构 (1&…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
