第9天----【位运算进阶之----按位取反(~)】(附补码,原码讲解)
今天我们来谈谈按位取反这件事。
简单来说,按位取反就是先将一个数写成其二进制表达形式,然后1变0,0变1。下面就让我们展开深入地讨论吧!

文章目录
- 一、预备知识:
- 1. 原码:
- 定义:
- 优缺点:
- 2. 补码:
- 定义:
- 优缺点:
- 二、按位取反:
- 三、拓展应用:
- 1. 巧求相反数:(不用`-`)
- 2. 代替减法(不用`-`实现减法)
- 3. 代替加法(不用`+`实现加法)
一、预备知识:
1. 原码:
定义:
✨原码是一种用二进制表示有符号整数的编码方式。其中,最高位表示符号位,0为正,1为负。其余位是数值位,表示数值的绝对值。
- 举个“栗子”来说:
- 1的原码是:001 ;
- -1的原码是:101 ;
✨我们可以看出,互为相反数的两个数的原码,除了第一位的符号位不一样以外,其余位都相同。(那么,可能有聪明的小伙伴们就想到了0,是不是0也有两种表达方式呢?果然聪明!在原码中,0和-0的表示是不一样的。)
优缺点:
- ❤️优点:简单直观,易于理解和计算。
- 💔缺点:加减法运算复杂,需要考虑符号位的处理。-0多占了一个数的表达位置,导致原码也可表示的总数减少了1个。
✨那可能又有小伙伴要问了,一个数很多吗?哈哈,一个-0单单看起来不多,但是一群-0不就多了吗?(这就告诉了我们"人多力量大"的道理,一个人可以走得很快,但一群人才能走得更远)。另外,-0的存在还会带来一些其他的问题:比如1️⃣(0)+(-0)=?2️⃣ 0和-0哪个大?
😢怎么一个原码事这么多?烦呐!下面就让我们来看看更为合适的编码方式–补码。
2. 补码:
❤️计算机中存储数据时,通常采用补码编码方式。
定义:
✨补码也是一种用于表示有符号整数的编码方式。其中,最高位(最左侧位)是符号位,0表示正数,1表示负数。其余位是数值位。
- 对于正数,补码就是其二进制原码本身。(看来不讲原码还不能开补码),如:数值+3的补码就是0011。
- 对于负数,补码是其对应正数的原码的各位取反,末位加一,符号位取1。
如:-3的补码可以通过三步得到:(因为+3的原码是0011)
1️⃣各位取反:1100
2️⃣末位加一:1101
3️⃣符号位取1:1101
优缺点:
-
❤️优点:
1️⃣加减法运算可以直接按位运算,无需特殊处理符号位。(相对原码来说更加方便)
2️⃣解决了原码中存在的正零和负零的问题。(-0的位置让给了最小的数)
3️⃣表示范围更加均衡。(补码的最小值的绝对值比最大值的绝对值多1) -
💔缺点:
1️⃣加减法时可能溢出。
2️⃣对称不明显。(看吧,上帝为你打开一扇窗的同时,也会为你关闭一扇门)
🐒当然,补码的知识宝库偌大无比,我现在只不过是揭开了其冰山一角,但对我们解决一般的问题来说,足够了。
二、按位取反:
✨将一个数的二进制表达的每一位取反,即0变为1,1变为0。取反符号用 "~" 表示。(从最低位(最右侧位)开始,逐位进行取反操作。)
例如,对于一个8位的二进制数10101010,按位取反后的结果是01010101。(注意,这是补码的取反哦)
下面来看几个具体的代码:
1️⃣1的按位取反:
#include<stdio.h>int main(void)
{int a = 0b1;printf("%d", ~a);return 0;
}
😄猜猜它的输出是多少? 输出0是不是?哈哈哈,是0你就上当了!

咦❓为什么❓为什么不是0❓ 1->0 没有问题啊❗️到底是哪里出错了❓会是哪里错了呢❓

阁下莫慌,我们慢慢来解释。
- 首先,a是一个
int类型,一般是4个字节(Byte),而一个字节是8位(8个bit),所以总共是32位。0b1是1的二进制表达,具体可以写为:00000000 00000000 00000000 00000001. - 下面我们对它进行取反操作,得:
11111111 11111111 11111111 11111110,但它是一个补码,我们以%d的形式输出就要得到它的十进制表达(可以理解为真值),那么问题来了,补码怎么转换成真值呢?考虑到具体的定义过于枯燥乏味,所以我直接告诉你转换的方法:可以先将补码转换为机器数,而计算机中的机器数一般用原码来表示,所以问题就转化为了补码->原码。 - 将补码的符号位不变,其余各位取反,末位加一。(这好像和原码转补码有点类似啊!)也就是:
10000000 00000000 00000000 00000001+1---> 10000000 00000000 00000000 00000010,再转换成十进制整数就是-2。
2️⃣0的按位取反:(%d的形式输出)
#include<stdio.h>int main(void)
{printf("%d", ~0);return 0;
}

2️⃣0的按位取反:(%u的形式输出)
#include<stdio.h>int main(void)
{printf("%u\n", ~0);printf("%lld", ((long long)1 << 32) - 1);return 0;
}

咦❓为啥同样是0,但取反后的输出结果不一样呢?
%d:有符号十进制整数的输出 (signed int):-2 ^ 31 -- 2 ^ 31 - 1%u:无符号十进制整数的输出 (unsigned int) :0 -- 2 ^ 32 - 1
这个有无符号具体就体现在是否有符号位,有符号位就少一位数值位,没有符号位就都是数值位。
- 0的补码:
00000000 00000000 00000000 00000000 - ~0的补码:
11111111 11111111 11111111 11111111
✨对于有符号整数来说,有正有负,且第一位是符号位。~0第一位是1,所以要转换成原码再输出:
即10000000 00000000 00000000 00000001,其值为-1;
✨对于无符号整数来说,没有符号位,32个位都是数值位,所以可以直接计算。因此,两者输出不同。
三、拓展应用:
1. 巧求相反数:(不用-)
✨相反数相必大家都知道,1的相反数是-1,0的相反数是0,简单来说一个数的相反数就是再其前面加个-
那么,不用这种方法还可以求相反数吗?
哈哈😄,其实这个问题我们上面已经说过了,直接利用补码的定义,求一个数的相反数,就是各位取反,末位加一。即-x=~x+1
#include<stdio.h>
int main(void)
{int x = -18;printf("%d的相反数是%d\n",x, ~x + 1);int y = 18;printf("%d的相反数是%d",y, ~y + 1);return 0;
}

(当然了,要注意数据的溢出问题。)
2. 代替减法(不用-实现减法)
✨现给定int类型的两个正数,不用-如何实现减法操作?
根据减法定义,减去一个数就等于加上这个数的相反数;
所以a - b = a + (-b) = a + (~b + 1);
#include<stdio.h>
int main(void)
{int a=1,b=2;printf("%d-%d=%d\n",a, b,a+~b+1);return 0;
}

3. 代替加法(不用+实现加法)
✨给定两个int类型的正数,不用+实现加法。根据加法定义,加上一个数等于减去一个数的相反数。即:a + b = a - (-b) = a - (~b +1)=a - ~b - 1;
#include<stdio.h>
int main(void)
{int a=1,b=2;printf("%d+%d=%d\n",a, b,a-(~b + 1));return 0;
}

好了,今天的讲解就到这里了,相信你也是收获满满吧!
终于肝完了,好累!!!

相关文章:

第9天----【位运算进阶之----按位取反(~)】(附补码,原码讲解)
今天我们来谈谈按位取反这件事。 简单来说,按位取反就是先将一个数写成其二进制表达形式,然后1变0,0变1。下面就让我们展开深入地讨论吧! 文章目录 一、预备知识:1. 原码:定义:优缺点ÿ…...

如何获取当前 JAR 包的存放位置?
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言代码中如何获取打包后的jar包存放的位置? 前言 代码中如何获取打包后的jar包存放的位置? 要获取当前运行的 JAR 包所存放的位置&#…...

微调llama2模型教程:创建自己的Python代码生成器
本文将演示如何使用PEFT、QLoRa和Huggingface对新的lama-2进行微调,生成自己的代码生成器。所以本文将重点展示如何定制自己的llama2,进行快速训练,以完成特定任务。 一些知识点 llama2相比于前一代,令牌数量增加了40%࿰…...

Java【手撕双指针】LeetCode 57. “两数之和“, 图文详解思路分析 + 代码
文章目录 前言一、两数之和1, 题目2, 思路分析3, 代码展示 前言 各位读者好, 我是小陈, 这是我的个人主页, 希望我的专栏能够帮助到你: 📕 JavaSE基础: 基础语法, 类和对象, 封装继承多态, 接口, 综合小练习图书管理系统等 📗 Java数据结构: 顺序表, 链表…...

大数据(一)定义、特性
大数据(一)定义、特性 本文目录: 一、写在前面的话 二、大数据定义 三、大数据特性 3.1、大数据的大量 (Volume) 特性 3.2、大数据的高速(Velocity)特性 3.3、大数据的多样化 (Variety) 特性 3.4、大数据的价值 (value) 特性 3.5、大…...
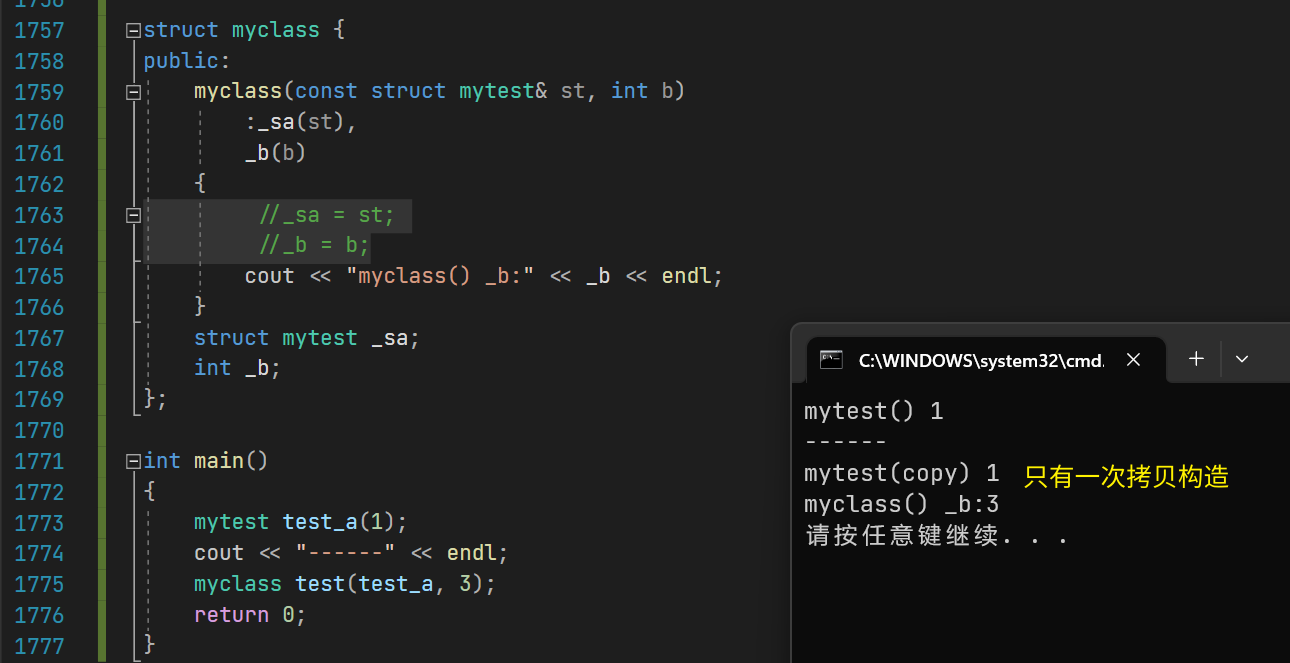
【C++】构造函数和初始化列表的性能差距
构造函数和初始化列表的性能差距对比测试 1.说明 在C类和对象中,你可能听到过更加推荐用初始化列表来初始化类内成员。如果类内成员是自定义类型,则只能在初始化列表中调用自定义类型的构造函数。 但初始化列表和在构造函数体内直接赋值有无性能差距呢…...

Linux下套接字TCP实现网络通信
Linux下套接字TCP实现网络通信 文章目录 Linux下套接字TCP实现网络通信1.引言2.具体实现2.1接口介绍1.socket()2.bind()3.listen()4.accept()5.connect() 2.2 服务器端server.hpp2.3服务端server.cc2.4客户端client.cc 1.引言 套接字(Socket)是计算机网络中实现网络通信的一…...

❤ vue清除定时器Bug
❤ vue清除定时器Bug 页面加载,清除定时器 clearTimeout(intm) 问题 遇见的需求是:webapp 从A页面进入B页面,B页面点击按钮,加载完B页面的加载效果进入c,从C页面返回A页面,仍然显示B页面的加载效果 结果定时器一直…...
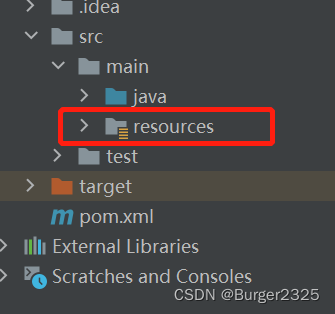
IDEA创建Spring,Maven项目没有resources文件夹
有时新建Spring或Maven项目时,会出现目录中main下无resources文件夹的情况,来一起解决一下: FIles|Project Structure 在Modules模块找到对应路径,在main下创建resources,右键main,选择新文件夹 输入文件…...
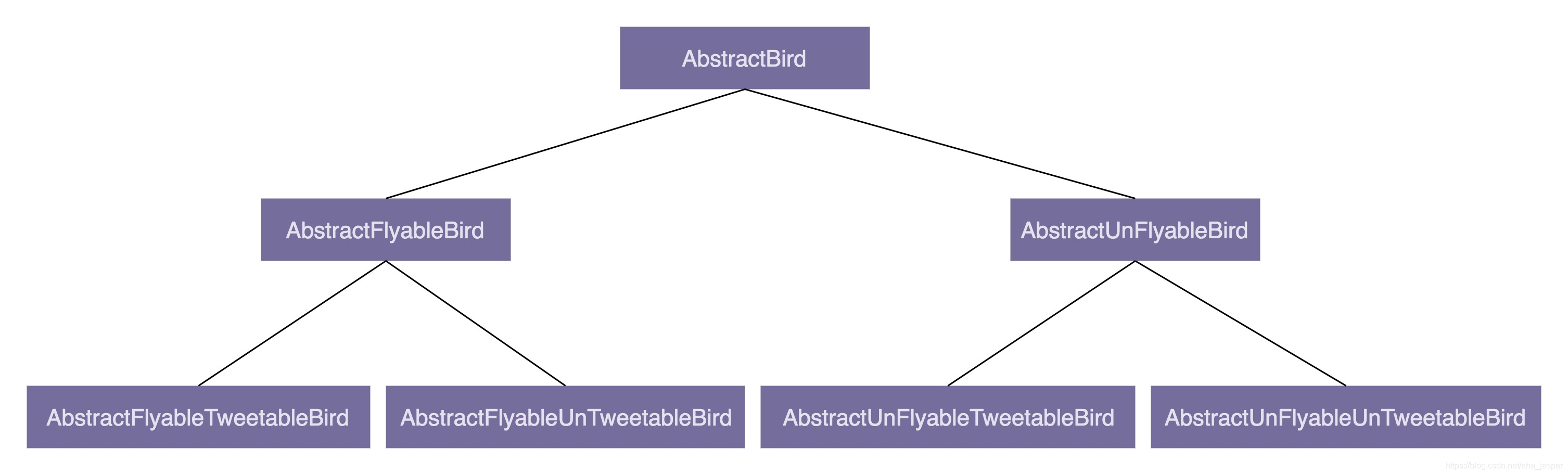
Unity 结构少继承多组合
为什么不推荐使用继承? 继承是面向对象的四大特性之一,用来表示类之间的 is-a 关系,可以解决代码复用的问题。虽然继承有诸多作用,但继承层次过深、过复杂,也会影响到代码的可维护性。所以,对于是否应该在…...

保研之旅2:中科院声学所“声学和信息学科”夏令营
💥💥💞💞欢迎来到本博客❤️❤️💥💥 本人持续分享更多关于电子通信专业内容以及嵌入式和单片机的知识,如果大家喜欢,别忘点个赞加个关注哦,让我们一起共同进步~ &#x…...

android adb自动连接手机安装apk bat
1.新建bat文件adb echo off:apk文件名称 在setting.txt获取 set apkFileName"":设置文件 set settingFileE:\apk\bat\setting.txt:启动页面 applicationid/启动页面路径 set startActivitycom.aaa.aaa/com.aaa.aaa.ui.common.SplashActivity:读取settingFile第一行的…...

用心维护好电脑,提高学习工作效率
无论是学习还是工作,电脑都是IT人必不可少的重要武器,一台好电脑除了自身配置要经得起考验,后期主人对它的维护也是决定它寿命的重要因素! 一、我的电脑 系统制造商: ASUSTeK COMPUTER INC. 系统型号: ZenBook UX481FAY 1.1 如…...

以太坊硬分叉后的可重入漏洞攻击
以太坊硬分叉后的可重入漏洞攻击 以太坊君士坦丁堡升级将降低部分 SSTORE 指令的 gas 费用。然而,这次升级也有一个副作用,在 Solidity 语言编写的智能合约中调用 address.transfer()函数或 address.send()函数时存在可重入漏洞。在目前版本的以太坊网络…...
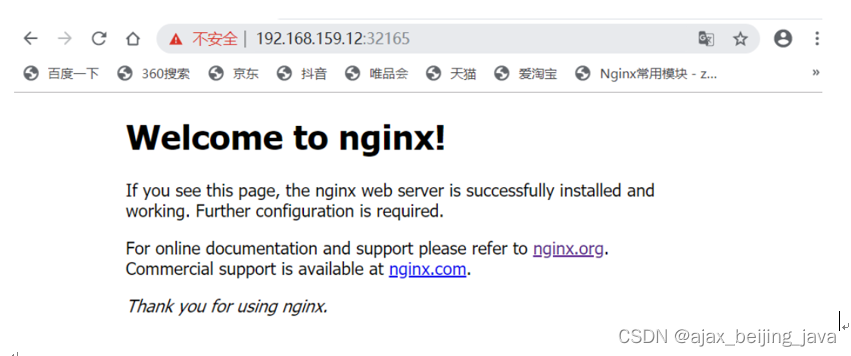
k8s 常用命令(三)
1、查看版本信息:kubectl version [rootmaster ~]# kubectl version [rootmaster ~]# kubectl version Client Version: version.Info{Major:"1", Minor:"21", GitVersion:"v1.21.3", GitCommit:"ca643a4d1f7bfe34773c74f7952…...

API 网关基础
目录 一、网关概述二、网关提供的功能三、常见网关系统3.1 Netflix Zuul3.2 Spring Cloud Gateway3.3 Kong3.4 APISIX3.5 Shenyu 一、网关概述 API网关是一个服务器,是系统的唯一入口。 从面向对象设计的角度看,它与外观模式类似。API网关封装了系统内部…...

【Linux】权限问题
Linux权限 一、Linux 权限的概念二、Linux 权限管理1. 文件访问者的分类2. 文件类型和访问权限(事物属性)3. 文件访问权限的相关设置方法 三、默认权限1. 对文件和目录进行操作需要的权限2. 文件和目录的默认权限3. 粘滞位 一、Linux 权限的概念 Linux …...
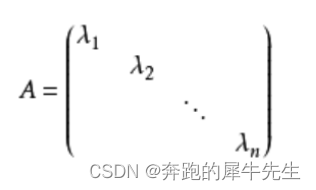
线性代数的学习和整理10:各种特殊类型的矩阵(草稿-----未完成 建设ing)
目录 1 图形化分类 1.1对称矩阵 1.2 梯形矩阵 1.3 三角矩阵 1.3.1 上三角矩阵 1.4 对角线矩阵 2 按各自功能分 2.1 等价矩阵 2.2 增广矩阵 2.3 伴随矩阵 2.4 正交矩阵 2.5 正交矩阵 2.6 相似矩阵 1 图形化分类 1.1对称矩阵 1.2 梯形矩阵 1.3 三角矩阵 1.3.1 上…...

Go 自学:变量、函数、结构体、接口、错误处理
1. 打印变量数据类型 package mainimport "fmt"func main() {penniesPerText : 2.0fmt.Printf("The type of penniesPerText is %T\n", penniesPerText) }输出为: The type of penniesPerText is float64 2. 同时给多个变量赋值 package mai…...

pyqt Pyton VTK 使用 滑块 改变 VTK Actor 颜色
使用 PyQt5 vtk vtk球体 使用滑块 RGB 改变 Actor 颜色 CODE import sys from PyQt5.QtWidgets import * from PyQt5.QtWidgets import (QApplication, QCheckBox, QGridLayout, QGroupBox,QMenu, QPushButton, QRadioButton, QVBoxLayout, QWidget, QSlider,QLineEdit,QLabe…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...
