机器学习之损失函数
深度学习中常用的损失函数多种多样,具体选择取决于任务类型和问题的性质。以下是一些常见的深度学习任务和相应的常用损失函数:
-
分类任务:
-
交叉熵损失函数(Cross-Entropy Loss):用于二分类和多类别分类任务,包括二元交叉熵(Binary Cross-Entropy)和多元交叉熵(Categorical Cross-Entropy)。
-
对数损失函数(Log Loss):与交叉熵损失函数类似,通常用于二分类问题。
-
带权重的交叉熵损失函数(Weighted Cross-Entropy Loss):适用于不平衡类别的分类任务,可以对不同类别的样本分配不同的权重。
-
Focal Loss:用于处理类别不平衡问题,可以调节对容易分类的样本和难以分类的样本的关注度。
-
-
回归任务:
-
均方误差损失函数(Mean Squared Error,MSE):用于回归问题,衡量模型的预测值与实际值之间的差异。
-
平均绝对误差损失函数(Mean Absolute Error,MAE):也用于回归问题,衡量模型的预测值与实际值之间的绝对差异。
-
Huber损失函数:对均方误差和平均绝对误差的折中,对异常值不敏感。
-
Log-Cosh 损失函数:对均方误差和平均绝对误差的折中,对异常值不敏感,并具有平滑性。
-
-
物体检测任务:
-
YOLO 损失函数:用于单阶段物体检测算法(如YOLO系列),包括位置损失、类别损失和置信度损失。
-
Faster R-CNN 损失函数:用于两阶段物体检测算法(如Faster R-CNN),包括区域建议网络(RPN)的分类损失和回归损失,以及目标检测网络(Fast R-CNN)的分类损失和回归损失。
-
-
语义分割任务:
-
交叉熵损失函数:通常用于像素级分类任务,每个像素被分类到不同的类别。
-
Dice 损失函数:用于语义分割,更适用于不平衡类别的情况。
-
-
生成对抗网络(GAN)任务:
-
生成器损失函数:通常使用对数似然损失(Log Likelihood Loss)或均方误差损失(MSE Loss)。
-
判别器损失函数:通常使用二元交叉熵损失(Binary Cross-Entropy Loss)。
-
相关文章:

机器学习之损失函数
深度学习中常用的损失函数多种多样,具体选择取决于任务类型和问题的性质。以下是一些常见的深度学习任务和相应的常用损失函数: 分类任务: 交叉熵损失函数(Cross-Entropy Loss):用于二分类和多类别分类任务…...

nacos适配SqlServer、Oracle
继上文《nacos适配达梦、瀚高、人大金仓数据库及部分源码探究 》后补充nacos适配SqlServer、Oracle的贴码,主要区别是SqlServer、Oracle的分页SQL有点不一样,做个记录; SqlServer的分页有三种实现方式:offset /fetch next、利用ma…...
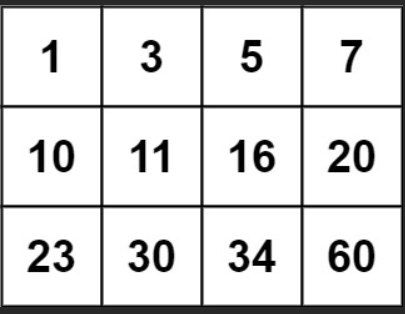
力扣:74. 搜索二维矩阵(Python3)
题目: 给你一个满足下述两条属性的 m x n 整数矩阵: 每行中的整数从左到右按非递减顺序排列。每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返…...

CPU、MCU、MPU、SOC、SOCPC、概念解释之在嵌入式领域常听到的名词含义
CPU、MCU、MPU、SOC等几个在嵌入式领域学习过程中会涉及到的几个名词。我们来学习一下,资料从网上搜集的,有错的地方可以指出。。。 CPU、MCU、MPU、SOC、SOCPC、 1. CPU2. MPU3.MCUMPU和MCU的区别:4.SOC5. SoPC 1. CPU CPU,即中…...
每日两题 111二叉树的最小深度 112路径总和(递归)
111 题目 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明:叶子节点是指没有子节点的节点。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:2示例 2&#x…...
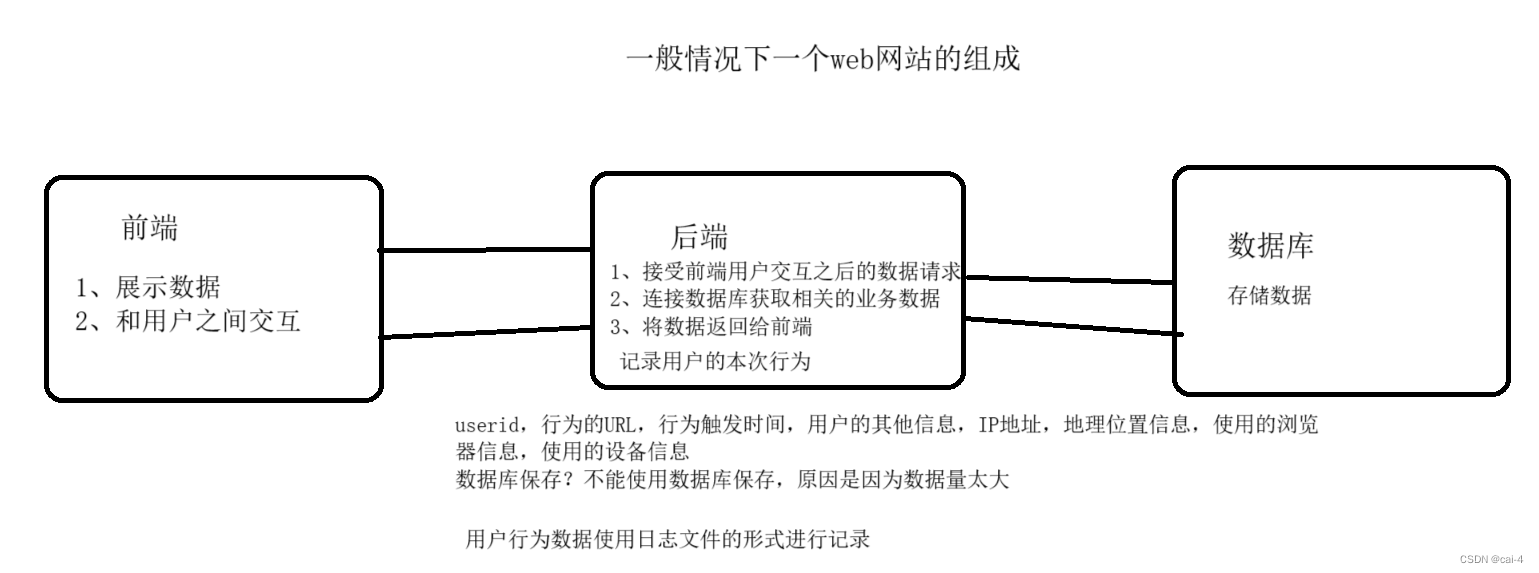
实训笔记8.24
实训笔记8.24 8.24笔记一、Sqoop数据迁移工具1.1 Sqoop的基本概念1.2 Sqoop的基本操作1.2.1 命令语法1.2.2 list-databases1.2.3 list-tables1.2.3 eval1.2.4 import1.2.5 export1.2.6 导入 二、Flume日志采集工具2.1 数据采集的问题2.2 数据采集一般使用的技术2.3 扩展&#x…...
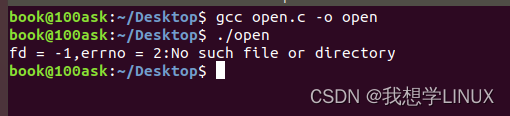
Linux下的系统编程——系统调用(五)
前言: 由操作系统实现并提供给外部应用程序的编程接口。(Application Programming Interface,API)。系统调用就是应用程序同系统之间数据交互的桥梁。 open/close函数 1.open函数: (1)int open(char *pathname, int flags) …...

动物体外受精手术VR模拟仿真培训系统保证学生及标本的安全
奶牛是养殖业主要的资源,因此保证奶牛的健康对养殖业的成功和可持续发展具有重要已用,奶牛有一些常见易发病,一旦处理不当,对奶牛业都会造成较大的经济损失,传统的奶牛手术培训实操难度大、风险高且花费大,…...
微信小程序|步骤条
步骤条是现代用户界面设计中常见的元素之一,它能够引导用户按照预定顺序完成一系列任务或步骤。在小程序中,实现步骤条可以为用户提供更好的导航和引导,使用户体验更加流畅和直观。本文将介绍如何在小程序中实现步骤条,并逐步展示实现的过程和关键技巧 目录 步骤条的作用及…...

如何才能设计出“好的”测试用例?
软件测试用例的设计质量直接影响到测试的完整性、有效性以及自动化测试的实施效果,是软件测试成功的重要保证,良好的软件测试用例对于提高测试的有效性和效率至关重要。那大家知道好的测试用例该怎么写吗?应该从哪几个方面来撰写呢࿱…...
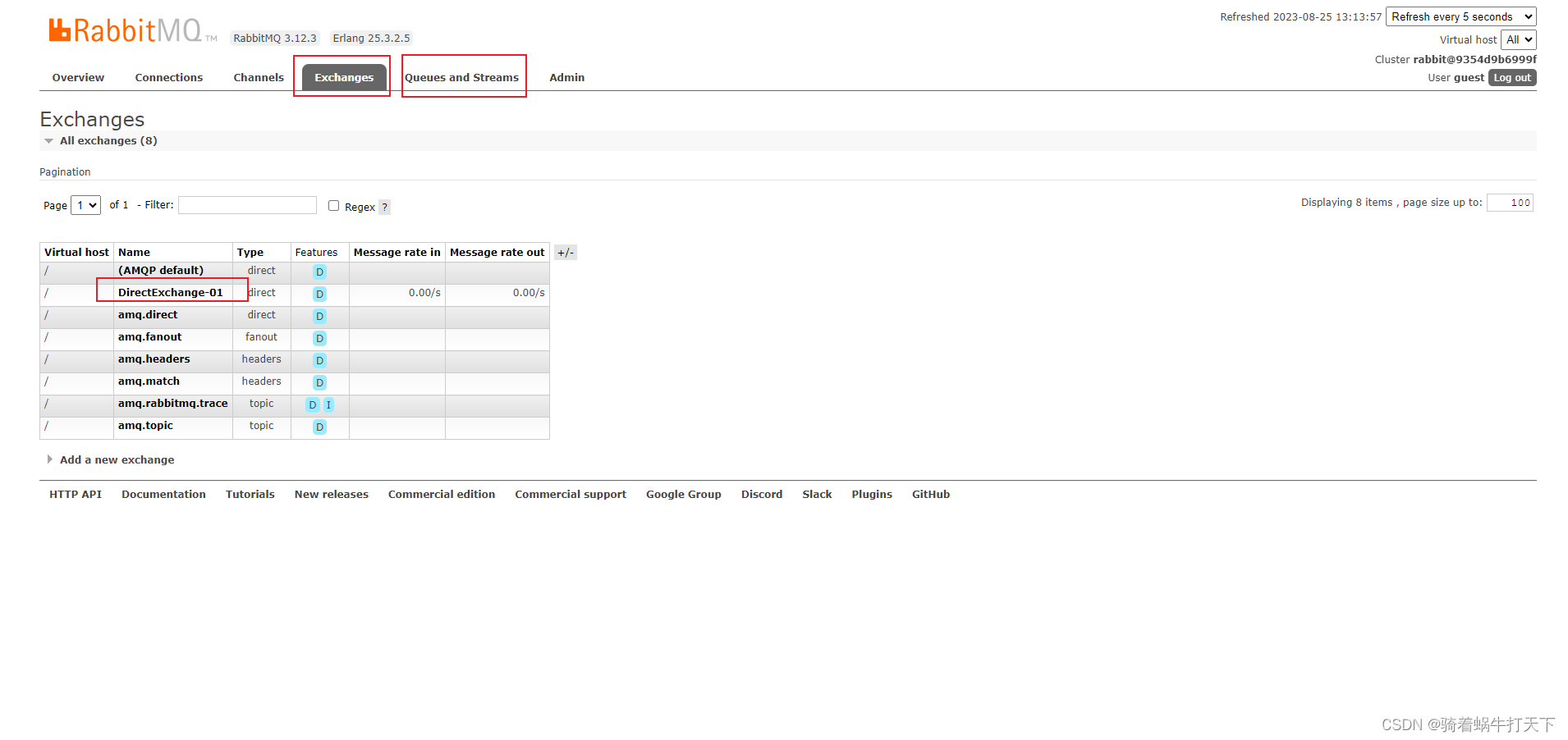
DirectExchange直连交换机
目录 一、简介 二、使用步骤 三、demo 父pom文件 pom文件 配置文件 config 消费者 生产者 测试 一、简介 直连型交换机,根据消息携带的路由键将消息投递给对应队列。 大致流程,有一个队列绑定到一个直连交换机上,同时赋予一个路由…...

Shell 编程:探索 Shell 的基本概念与用法
目录 Shell 简介 Shell 脚本 Shell 脚本运行 Shell 变量 1、创建变量和赋值 2、引用变量 3、修改变量的值 4、只读变量 5、删除变量 6、环境变量 Shell 字符串操作 1、拼接字符串 2、字符串长度 3、字符串截取 Shell 数组 1、创建数组 2、访问数组元素 shell …...
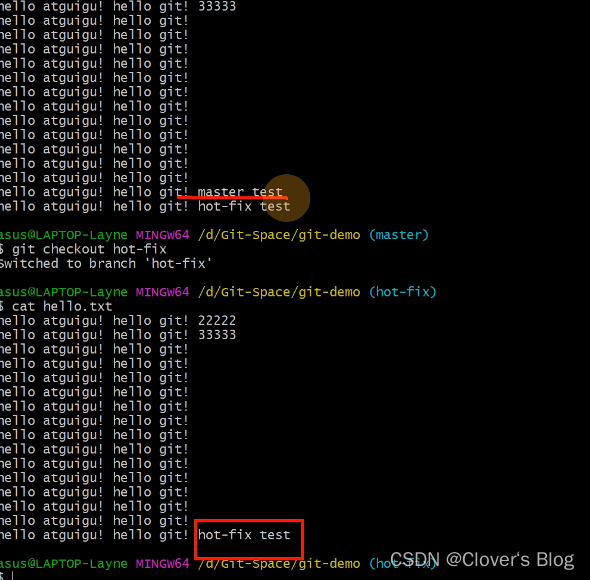
【Git分支操作---讲解二】
Git分支操作---讲解二 查看分支创建分支切换分支修改分支切换分支合并分支合并分支【冲突】(只会修改主分支不会修改其他分支)什么时候会有冲突? 查看分支 创建分支 切换分支 修改分支 切换分支 合并分支 合并分支【冲突】(只会修改主分支不会修改其他分支) 什么时…...

vue2+qrcodejs2+clipboard——实现二维码展示+下载+复制到剪切板——基础积累
最近在写后台管理系统时,遇到一个需求就是要实现二维码的展示下载复制到剪切板。 效果图如下: 1.二维码展示下载功能——qrcodejs20.0.2 我是安装的qrcodejs20.0.2,指定了具体的版本号,也可以安装默认的当前稳定版本࿰…...

【PHP】echo 输出数组报Array to string conversion解决办法
代码: <?PHP echo "Hello World!";$demoName array("kexuexiong","xiong");echo "<pre>";var_dump($demoName);echo $demoName; print_r($demoName);echo "</pre>"; ?>输出结果࿱…...
)
Arduino驱动MiCS-4514气体传感器(气体传感器篇)
目录 1、传感器特性 2、控制器和传感器连线图 3、驱动程序...

marked在vue项目中改变超链接跳转方式和图片放大预览
marked在vue项目中改变超链接跳转方式和图片放大预览 这里我是另起一个js文件对marked的配置做了修改,参考如下 import marked from marked let renderer new marked.Renderer() const linkRenderer renderer.link const imgRenderer renderer.image // 超链接…...
leetcode485. 最大连续 1 的个数
思路:【双指针】 left左边界,right往右跑遇到0,则计算该长度。并更新cnt(最大连续1个数)。 class Solution { public:int findMaxConsecutiveOnes(vector<int>& nums) {int left 0, right 0;int cnt 0;…...

linux 源代码编译
源代码编译 有时候会在linux上下载源码包,然后进行编译成可执行的文件,这个过程需要经过configure、make、make install、make clean四个步骤 configure 为这个程序在当前的操作系统环境下选择合适的编译器和环境参数来编译该代码 make 对程序代码进行编…...

C语言日常刷题 1
文章目录 题目答案与解析1234.5.6. 题目 1、执行下面程序,正确的输出是( ) int x5,y7; void swap() { int z; zx; xy; yz; } int main() { int x3,y8; swap(); printf(“%d,%d\n”,x, y); return 0; } A: 5,7 B: 7,5 C: 3,8 D: 8…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
