线性代数的学习和整理4: 求逆矩阵的多种方法汇总
目录
原始问题:如何求逆矩阵?
1 EXCEL里,直接可以用黑盒表内公式 minverse() 数组公式求A-
2 非线性代数方法:解方程组的方法
3 增广矩阵的方法
4 用行列式的方法计算(未验证)
5 A-=1/|A|*A* (未验证)
原始问题:如何求逆矩阵?
求逆矩阵的方法很多
- 方法1:矩形计算展开为方程组,解方程组得出A-的各个元素
- 方法2:利用增广矩阵,进行线性变换来求A-
- 方法3:行列数的方法
- 方法4
1 EXCEL里,直接可以用黑盒表内公式 minverse() 数组公式求A-
- 除了各种手动计算的方法,EXCEL可以使用 minverse() 函数计算逆矩阵
- 只要提前选好多个单元格,输入数组公式miniverse()即可,结果是没问题
- 错误点:选中的单元格范围不对,没有按shift+ctrl+enter 三键输入数组公式

2 非线性代数方法:解方程组的方法
这种方法理论上纯粹用函数方程组即可
- 设置逆矩阵的内部数据分别为变量x1,x2....
- 利用利用 A*A- =I, 也就是这2个矩阵相乘*逆矩阵=I
- 形成的方程组解方程求出x1,x2....
- 从而就可以计算出 逆矩阵

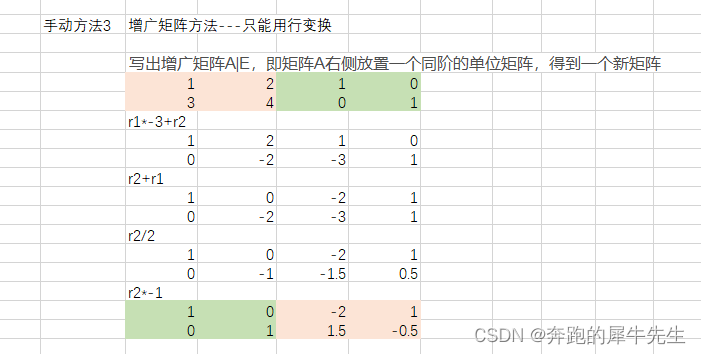
3 增广矩阵的方法
- 使用增广矩阵变幻时,只能用行变换,不能用列变换。因为如果用列变换,会影响 I的列和矩阵的列的混乱
- 使用增广矩阵进行行变换,让A*I=I*A- 即可求出逆矩阵A-
4 用行列式的方法计算(未验证)
这个方法不是我的,来源
用这个方法求逆矩阵:稳如狗让一切繁琐问题都有其猥琐解法https://mp.weixin.qq.com/s?__biz=MzIxMDM0Mjg1Mw==&mid=2247483954&idx=1&sn=27f233069f43f8c0ce3d4e6c135a0de8&chksm=97674498a010cd8e0cb7e6285f3fd51d76e4113f80d5cc00a5888cb405efd07bd153611ba97b&scene=27


5 A-=1/|A|*A* (未验证)

相关文章:

线性代数的学习和整理4: 求逆矩阵的多种方法汇总
目录 原始问题:如何求逆矩阵? 1 EXCEL里,直接可以用黑盒表内公式 minverse() 数组公式求A- 2 非线性代数方法:解方程组的方法 3 增广矩阵的方法 4 用行列式的方法计算(未验证) 5 A-1/|A|*A* &…...

【C#学习笔记】匿名函数和lambda表达式
文章目录 匿名函数匿名函数的定义匿名函数作为参数传递匿名函数的缺点 lambda表达式什么是lambda表达式闭包 匿名函数 为什么我们要使用匿名函数?匿名函数存在的意义是为了简化一些函数的定义,特别是那些定义了之后只会被调用一次的函数,与其…...

百度Apollo:引领自动驾驶技术创新的先锋
文章目录 前言一、内容总结 前言 大家好,我是萝卜头不吃萝卜头,今天和大家分享一下我学习百度Apollo自动驾驶的心得。 在七月份的时候,我收到了Apollo开发者社区的邀请,进行学习Apollo自动驾驶汽车的2023星火培训训练,…...
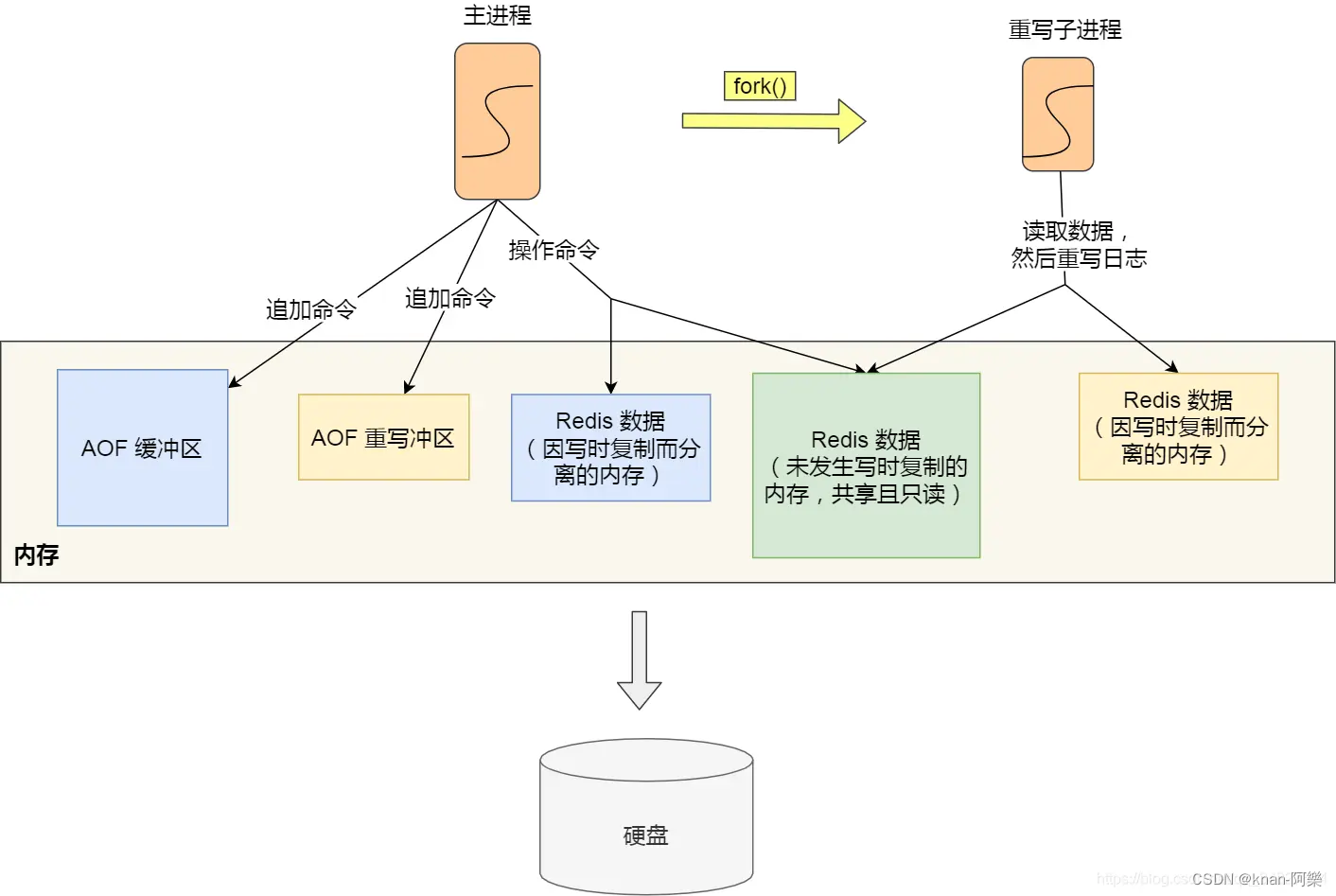
Redis 重写 AOF 日志期间,主进程可以正常处理命令吗?
重写 AOF 日志的过程是怎样的? Redis 的重写 AOF 过程是由后台子进程 bgrewriteaof 来完成的,这么做有以下两个好处。 子进程进行 AOF 重写期间,主进程可以继续处理命令请求,从而避免阻塞主进程子进程带有主进程的数据副本。这里…...
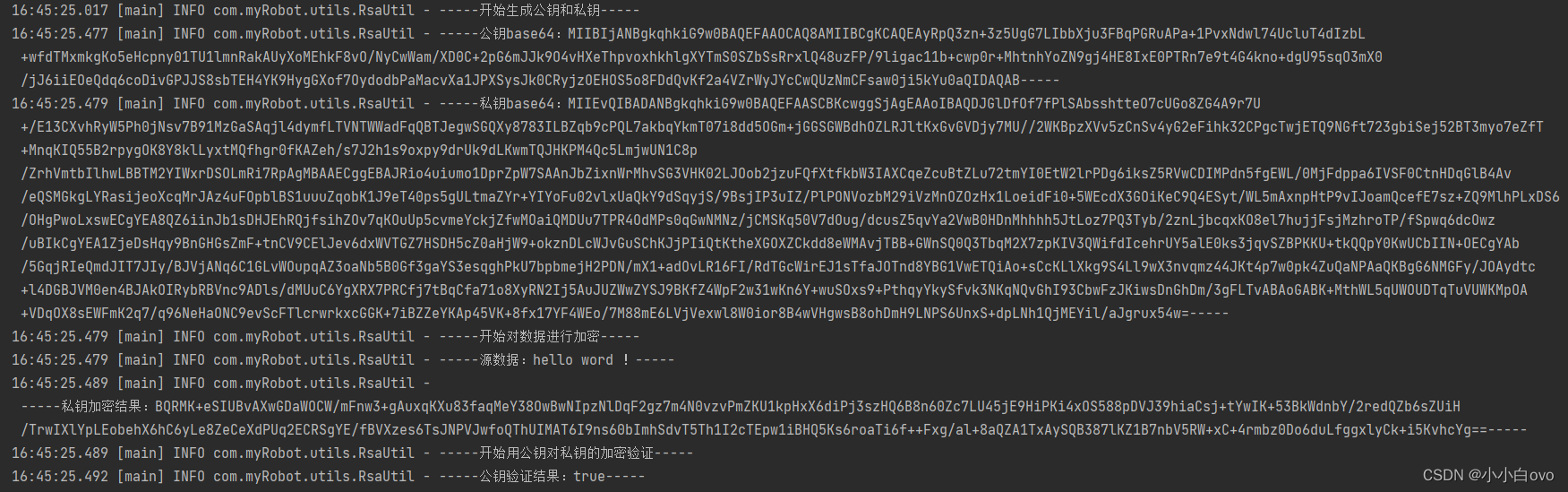
java实现生成RSA公私钥、SHA256withRSA加密以及验证工具类
前言: RSA属于非对称加密。所谓非对称加密,需要两个密钥:公钥 (publickey) 和私钥 (privatekey)。公钥和私钥是一对,如果用公钥对数据加密,那么只能用对应的私钥解密。如果用私钥对数据加密,只能用对应的公…...
lab7 thread
文章目录 Uthread: switching between threadstaskhints思路上下文的恢复和保存thread_createthread_schedule Using threads思路 Barrier Uthread: switching between threads 在这个练习中,你将为一个用户级别线程系统设计上下文切换机制,并实现它。 …...

接口自动化测试:mock server之Moco工具
什么是mock server mock:英文可以翻译为模仿的,mock server是我们用来解除依赖(耦合),假装实现的技术,比如说,前端需要使用某些api进行调试,但是服务端并没有开发完成这些api&#…...
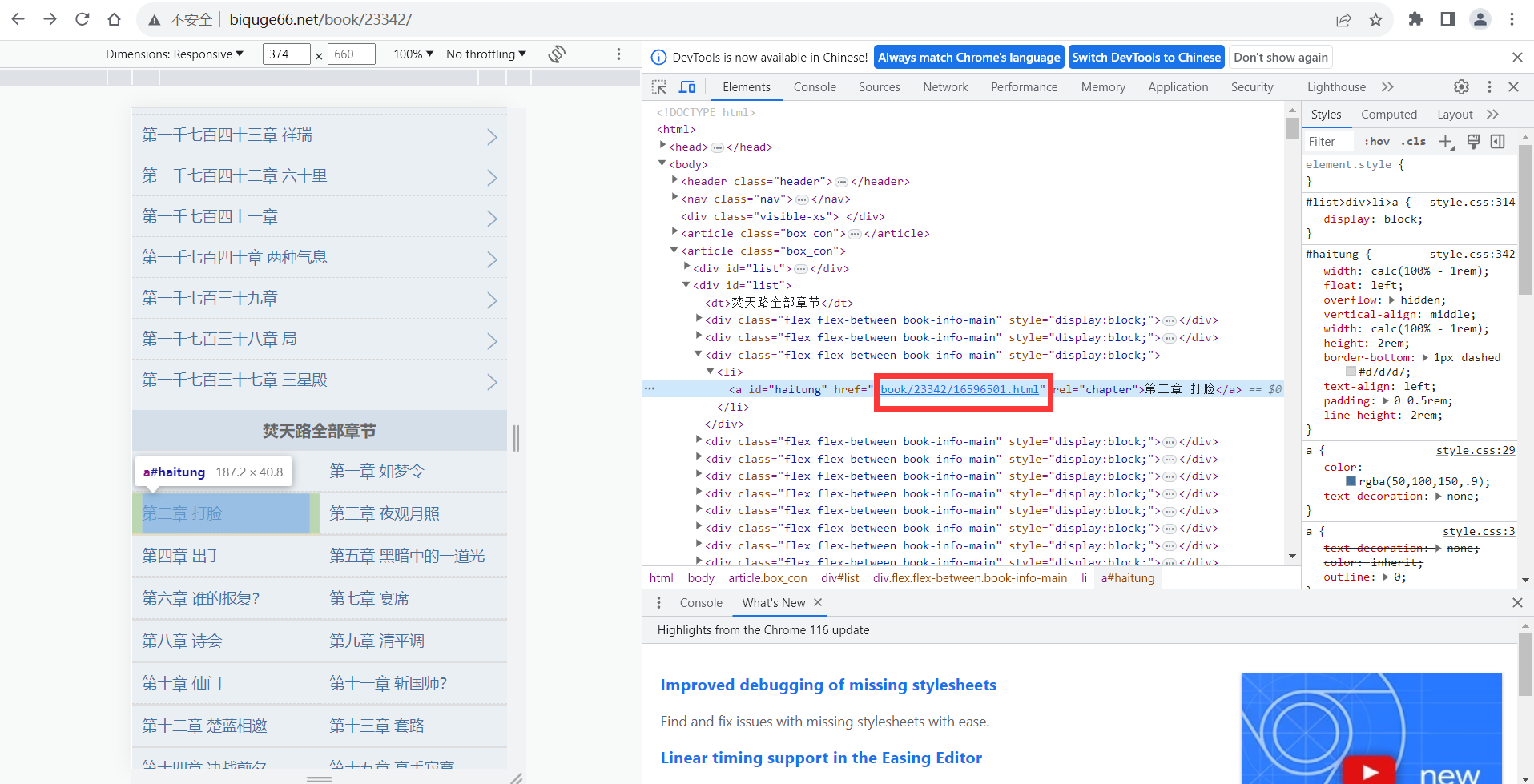
用python从零开始做一个最简单的小说爬虫带GUI界面(2/3)
目录 前一章博客 前言 主函数的代码实现 逐行代码解析 获取链接 获取标题 获取网页源代码 获取各个文章的链接 函数的代码 导入库文件 获取文章的标题 获取文章的源代码 提取文章目录的各个文章的链接 总代码 下一章内容 前一章博客 用python从零开始做一个最简单…...

CEF 缓存处理:清理缓存、禁用缓存、忽略缓存
目录 一、CEF缓存处理 1、指定缓存路径 2、清理缓存 3、禁用缓存 1)、原理分析...
Android 系统桌面 App —— Launcher 开发(1)
Android 系统桌面 App —— Launcher 开发(1) Launcher简介 Launcher就是Android系统的桌面,俗称“HomeScreen”也就是我们开机后看到的第一个App。launcher其实就是一个app,它的作用是显示和管理手机上其他App。目前市场上有很…...
一个程序员的工作日记--每天就干两件事,一年后让别人刮目相看
文章目录 成功源于专注一、早上布局二、晚上复盘三、技术细节四、专注与成功五、专注的重要性六、忙碌和赚钱七、结论以嵌入式开发为例:一、早上布局二、晚上复盘三、技术细节四、专注与成功五、忙碌和赚钱六、结论在嵌入式软件开发中,我们需要按照以下步…...

Linux虚拟机安装(Ubuntu 20)
最近这段时间使用VMWare安装了一下Ubuntu版本的Linux虚拟机,在这里记录一下安装时参考的文章以及需要注意的细节 参考链接: VMware虚拟机下安装Ubuntu20.04(保姆级教程) 一、安装VMWare 下载链接:VMware Workstatio…...

1.6 服务器处理客户端请求
客户端进程向服务器进程发送一段文本(MySQL语句),服务器进程处理后再向客户端进程发送一段文本(处理结果)。 从图中我们可以看出,服务器程序处理来自客户端的查询请求大致需要经过三个部分,分别…...

火山引擎发布自研视频编解码芯片 压缩效率提升30%
8月22日,火山引擎视频云宣布其自研的视频编解码芯片已成功出片。经验证,该芯片的视频压缩效率相比行业主流硬件编码器可提升30%以上,未来将服务于抖音、西瓜视频等视频业务,并将通过火山引擎视频云开放给企业客户。 火山引擎总裁…...
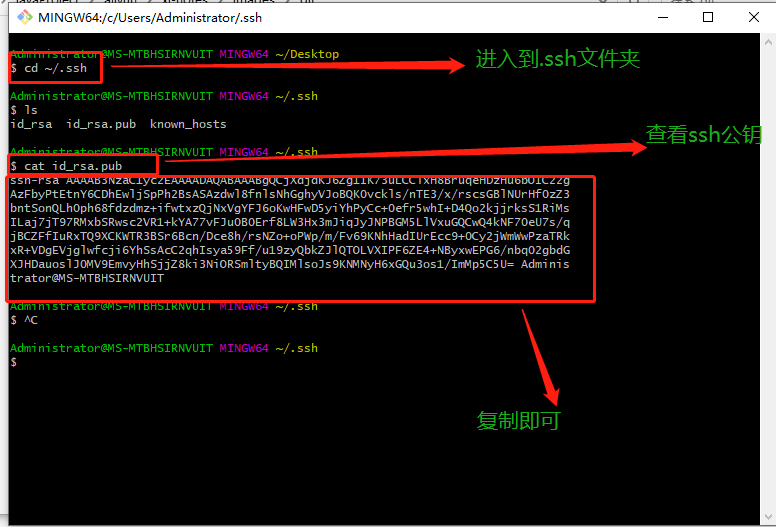
从头开始:将新项目上传至Git仓库的简易指南
无论您是一个经验丰富的开发者还是一个刚刚起步的新手,使用Git来管理您的项目是一个明智的选择。Git是一个强大的版本控制系统,它可以帮助您跟踪项目的变化、合并代码以及与团队成员协作。在本文中,我们将为您提供一步步的指南,教…...

数据库的增量备份与差异备份
在当今数字时代,数据已经成为公司的主要资产。为了维护这些珍贵的数据,公司通常会采取各种数据保护措施,其中增量备份是一种很有效的方法。本文将详细介绍什么是数据库的增量备份,以及如何帮助企业更有效地维护数据。 我们需要…...

视频云存储/安防监控视频智能分析网关V3:占道经营功能详解
违规占道经营者经常会在人流量大、车辆集中的道路两旁摆摊,导致公路交通堵塞,给居民出行的造成不便,而且违规占路密集的地方都是交通事故频频发生的区域。 TSINGSEE青犀视频云存储/安防监控视频/AI智能分析网关V3运用视频AI智能分析技术&…...

卡尔曼滤波学习笔记
Kalman Filter Ⅰ、直观理解1、描述2、例子 Ⅱ、适用范围1、线性系统2、噪声服从高斯分布 Ⅲ、相关公式1、原始公式2、预测公式3、更新公式4、初值赋予5、总结 Ⅳ、应用例子Ⅴ、代码实现Ⅵ、公式理解1、协方差矩阵的理解1.1 协方差1.2 协方差矩阵1.3、相关数学公式 2、状态方程…...

NLP预训练模型超大规模探索
总共从四方面来进行比较。 第一个方面,高层次方法(自监督的预训练方法)对比,总共三种方式。 语言模型式,就是 GPT-2 那种方式,从左到右预测;BERT-style 式,就是像 BERT 一样将一部…...
)
OpenCV实战系列总目录(更新中)
1、openCV实战-系列教程1:基本操作(环境配置/图像读取打印/视频读取打印/图像裁剪/颜色通道提取/边界填充/数值计算)、源码解读 openCV实战-系列教程1:基本操作(环境配置/图像读取打印/视频读取打印/图像裁剪/颜色通道…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
:处理原始数据命令)
ffmpeg(三):处理原始数据命令
FFmpeg 可以直接处理原始音频和视频数据(Raw PCM、YUV 等),常见场景包括: 将原始 YUV 图像编码为 H.264 视频将 PCM 音频编码为 AAC 或 MP3对原始音视频数据进行封装(如封装为 MP4、TS) 处理原始 YUV 视频…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...
无头浏览器技术:Python爬虫如何精准模拟搜索点击
1. 无头浏览器技术概述 1.1 什么是无头浏览器? 无头浏览器是一种没有图形用户界面(GUI)的浏览器,它通过程序控制浏览器内核(如Chromium、Firefox)执行页面加载、JavaScript渲染、表单提交等操作。由于不渲…...
