深度学习调参技巧
写完代码—> 小数据上降loss无nan—> 大数据没爆卡速度可以—> 实验log完好可视化loss稳步下降—>回头看实验结果
- 写完代码后,不要只是在小数据上降loss无nan,还要检查一下模型的输出是否符合预期,比如是否有明显的偏差或者异常值。
- 大数据没爆卡速度可以是一个好的指标,但是也要注意模型的泛化能力,比如是否有过拟合或者欠拟合的现象。你可以使用交叉验证或者早停法来避免过拟合,或者增加模型的复杂度或者数据的多样性来避免欠拟合。
- 实验log完好可视化loss稳步下降是一个好的习惯,但是也要关注一下其他的评价指标,比如准确率、召回率、F1值等。这些指标可以反映模型在不同方面的性能,比如是否有偏向于某一类别或者某一样本的问题。
关于欠拟合:
欠拟合的现象是指模型在训练集和测试集上都表现不好,即模型的拟合能力不足,无法捕捉数据的真实规律。欠拟合的原因可能有以下几种:
- 模型的复杂度太低,比如使用线性模型来拟合非线性数据,或者使用过少的神经元或者隐藏层来构建深度学习模型。
- 数据的质量或者数量不够,比如数据存在噪声、缺失值、异常值等,或者数据的分布不均匀、不具有代表性等。
- 训练的时间或者次数不够,比如使用过小的学习率或者过大的批次大小来进行梯度下降,或者使用过早的停止条件来终止训练。
欠拟合的现象可以通过以下几种方法来解决:
- 增加模型的复杂度,比如使用非线性模型来拟合非线性数据,或者使用更多的神经元或者隐藏层来构建深度学习模型。
- 提高数据的质量或者数量,比如对数据进行清洗、填补、标准化等预处理操作,或者使用数据增强、生成对抗网络等技术来扩充数据集。
- 延长训练的时间或者次数,比如使用合适的学习率或者批次大小来进行梯度下降,或者使用交叉验证、学习曲线等方法来确定最佳的停止条件。
相关文章:

深度学习调参技巧
写完代码—> 小数据上降loss无nan—> 大数据没爆卡速度可以—> 实验log完好可视化loss稳步下降—>回头看实验结果 写完代码后,不要只是在小数据上降loss无nan,还要检查一下模型的输出是否符合预期,比如是否有明显的偏差或者异常值…...
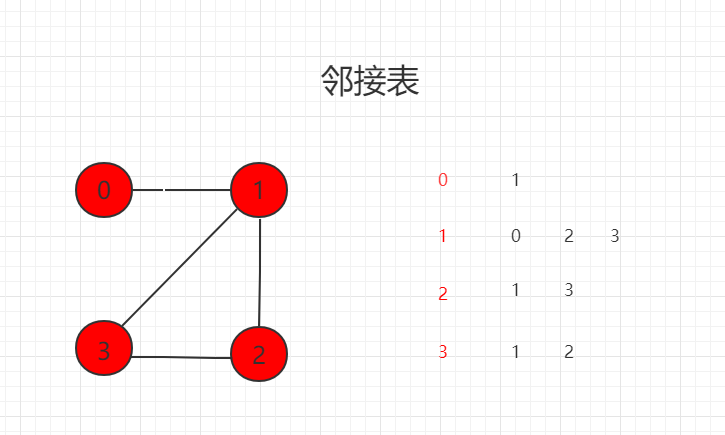
图论基础和表示(Java 实例代码)
目录 图论基础和表示 一、概念及其介绍 二、适用说明 三、图的表达形式 Java 实例代码 src/runoob/graph/DenseGraph.java 文件代码: src/runoob/graph/SparseGraph.java 文件代码: 图论基础和表示 一、概念及其介绍 图论(Graph Theory)是离散数…...

各种数据库查询报错问题
文章目录 前言一、约束条件是自增,不能直接添加数据二、使用步骤1.引入库2.读入数据 总结 前言 记录常见的数据库使用问题,以及对应解决思路 一、约束条件是自增,不能直接添加数据 消息 8101,级别 16,状态 1…...

人效九宫格城市沙龙暨《人效九宫格白皮书》发布会 —上海站,圆满结束
8月11日,在上海龙之梦万丽酒店,由盖雅工场主办的人效九宫格城市沙龙暨《人效九宫格白皮书》发布会 —上海站,圆满结束。 近百位来自多个行业的企业管理者及人力资源从业者汇聚一堂,共同探讨企业如何将盈利模式从数量增长转为质量增…...

【C语言】文件操作 -- 详解
一、什么是文件 磁盘上的文件是文件。 1、为什么要使用文件 举个例子,当我们想实现一个 “通讯录” 程序时,在通讯录中新建联系人、删除联系人等一系列操作,此时的数据存储于内存中,程序退出后所有数据都会随之消失。为了让通讯录…...

飞天使-k8s基础组件分析-持久化存储
文章目录 emptyDirhostpathpv和pvc介绍nfs作为静态pv案例nfs作为动态pv案例使用本地文件夹作为pv改变默认存储类及回收策略参考文档 emptyDir 重启文件还有,但是如果杀了进程,则会丢失文件 创建pod # kubectl apply –f redis.yaml校验pod是否处于运行&…...
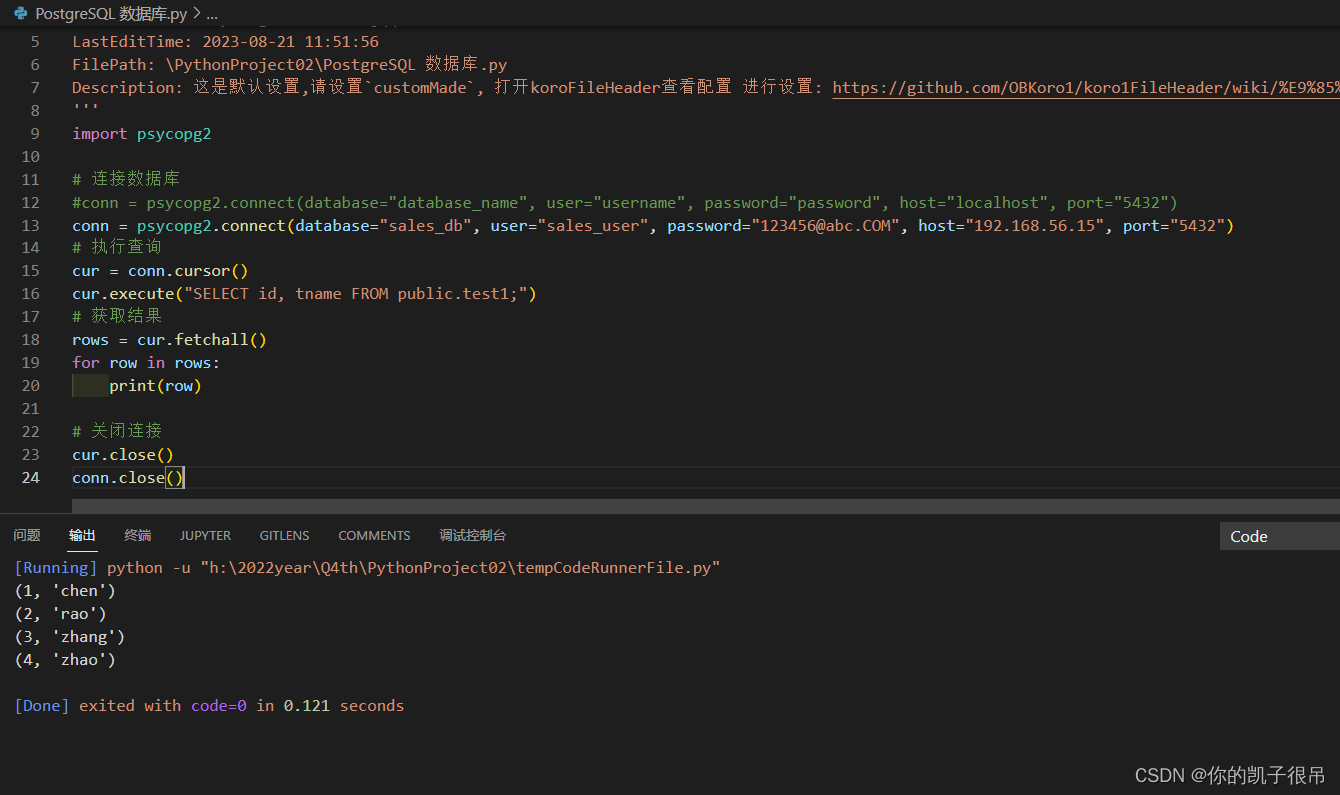
python连接PostgreSQL 数据库
执行如下命令安装 pip3 install psycopg2 python代码 Author: tkhywang 2810248865qq.com Date: 2023-08-21 11:42:17 LastEditors: tkhywang 2810248865qq.com LastEditTime: 2023-08-21 11:51:56 FilePath: \PythonProject02\PostgreSQL 数据库.py Description: 这是默认设置…...
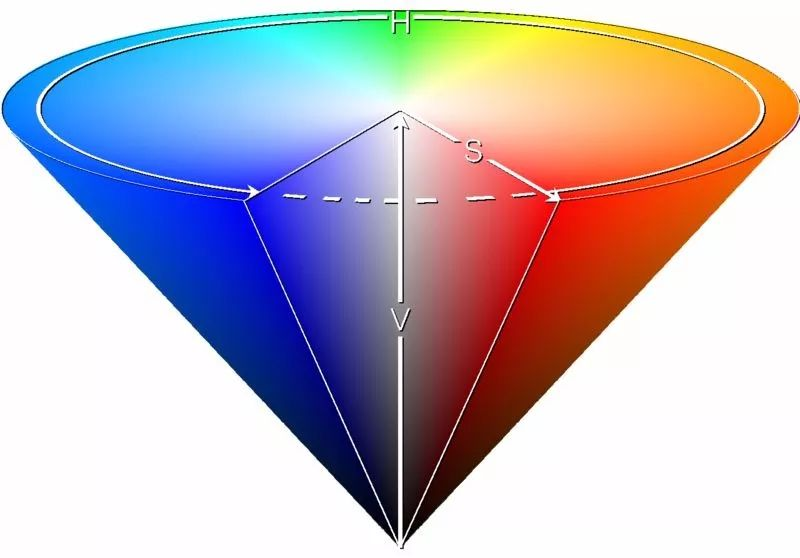
数字图像处理—— Lab、YCbCr、HSV、RGB之间互转
Lab “Lab” 图像格式通常指的是 CIELAB 色彩空间,也称为 Lab 色彩空间。它是一种用于描述人类视觉感知的颜色的设备无关色彩空间,与常见的 RGB 和 CMYK 色彩空间不同。CIELAB 由国际照明委员会(CIE)于1976年定义,用于…...

自动驾驶SLAM技术第四章习题2
在g2o的基础上改成ceres优化,高博都写好了其他的部分, 后面改ceres就很简单了. 这块我用的是ceres的自动求导,很方便,就是转化为模板仿函数的时候有点麻烦, 代码部分如下 ceres_type.h : ceres优化核心库的头文件 这个文件写的内…...

vue拖拽div盒子实现上下拖动互换
vue拖拽div盒子实现上下拖动互换 <div v-for"(item, index) in formList" :key"index" draggable"true"dragstart"handleDragStart($event, item)"dragenter"handleDragEnter($event, item)"dragover.prevent"han…...
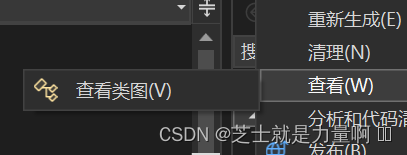
Visual Studio 2022 右键单击项目没有出现View | View Class Diagram(Visual Studio 无法使用类设计器)
文章目录 问题描述原因.NET Core项目.NET Framework项目 问题描述 当我们在Solution Explorer窗口右键单击项目时,快捷菜单中没有出现“查看”,或者出现了“查看”,但是“查看”里没有View Class Diagram。 原因 首先你要确保你安装了类设…...

EFCore常见用法
EFCore官方文档置顶,看这个就行。下面的内容只是总结,算是备忘录。 一、创建和删除 //1、创建数据库和表 db.Database.EnsureCreated();//将创建数据库(如果不存在)并初始化数据库架构。 如果存在任何表 (包括另一 DbContext 类)…...

概率论与数理统计:第六章:数理统计
文章目录 Ch6. 数理统计(一) 总体与样本(二) 统计量 (5个)2.5个常用统计量3.矩的概念 (三) 抽样分布 (3个)0.上α分位点1.χ分布2.t分布3.F分布 (四) 抽样分布定理1.单个正态总体2.两个正态总体 Ch6. 数理统计 (一) 总体与样本 1.概念: (1)总体 (2)样本 简单随机…...
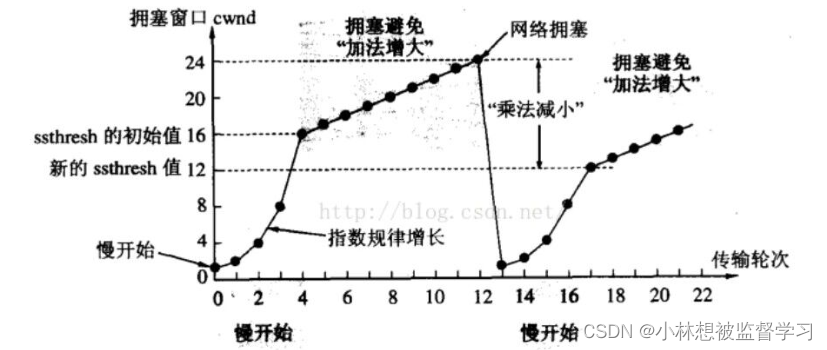
拥塞控制(TCP限制窗口大小的机制)
拥塞控制机制可以使滑动窗口在保证可靠性的前提下,提高传输效率 关于滑动窗口的属性以及部分机制推荐看TCP中窗口和滑动窗口的含义以及流量控制 拥塞控制出现的原因 看了上面推荐的博客我们已经知道了,由于接收方接收数据的能力有限,所以要通…...

校园供水系统智能管理
import pandas as pd data1pd.read_excel("C://Users//JJH//Desktop//E//附件_一季度.xlsx") data2pd.read_excel("C://Users//JJH//Desktop//E//附件_二季度.xlsx") data3pd.read_excel("C://Users//JJH//Desktop//E//附件_三季度.xlsx") data4…...

Flask-SocketIO和Flask-Login联合开发socketio权限系统
设置 Flask, Flask-SocketIO, Flask-Login: 首先,确保安装了必要的库: pip install Flask Flask-SocketIO Flask-Login基础设置: from flask import Flask, render_template, redirect, url_for, request from flask_socketio import SocketIO, emit from flask_…...

航空电子设备中的TSN通讯架构—直升机
前言 以太网正在迅速取代传统网络,成为航空电子设备和任务系统的核心高速网络。本文提出了以太网时间敏感网络(TSN)在航空电子设备上应用的技术优势问题。在实际应用中,TSN已成为一个具有丰富的机制和协议的工具箱,可满足与时间和可靠性相关…...

elment-ui中使用el-steps案例
el-steps案例 样式 代码 <div class"active-box"><div class"active-title">请完善</div><el-steps :active"active" finish-status"success" align-center><el-step title"第一步" /><…...

FPGA解析串口指令控制spi flash完成连续写、读、擦除数据
前言 最近在收拾抽屉时找到一个某宝的spi flash模块,如下图所示,我就想用能不能串口来读写flash,大致过程就是,串口向fpga发送一条指令,fpga解析出指令控制flah,这个指令协议目前就是: 55 AA …...

msvcp120.dll丢失的解决方法,分享三种快速修复的方法
今天,我将和大家分享一个关于电脑问题的解决方法——msvcp120.dll丢失的解决方法。希望对大家有所帮助。 首先,让我们来了解一下msvcp120.dll文件。msvcp120.dll是Microsoft Visual C 2010 Redistributable Package的一个组件,它包含了一些运…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
