2023年高教社杯数学建模思路 - 案例:FPTree-频繁模式树算法
文章目录
- 算法介绍
- FP树表示法
- 构建FP树
- 实现代码
- 建模资料
## 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
算法介绍
FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,他与Apriori算法一样也是用来挖掘频繁项集的,不过不同的是,FP-Tree算法是Apriori算法的优化处理,他解决了Apriori算法在过程中会产生大量的候选集的问题,而FP-Tree算法则是发现频繁模式而不产生候选集。但是频繁模式挖掘出来后,产生关联规则的步骤还是和Apriori是一样的。
常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FP-growth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。
FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。
FP树表示法
FP树通过逐个读入事务,并把事务映射到FP树中的一条路径来构造。由于不同的事务可能会有若干个相同的项,因此它们的路径可能部分重叠。路径相互重叠越多,使用FP树结构获得的压缩效果越好;如果FP树足够小,能够存放在内存中,就可以直接从这个内存中的结构提取频繁项集,而不必重复地扫描存放在硬盘上的数据。
一颗FP树如下图所示:
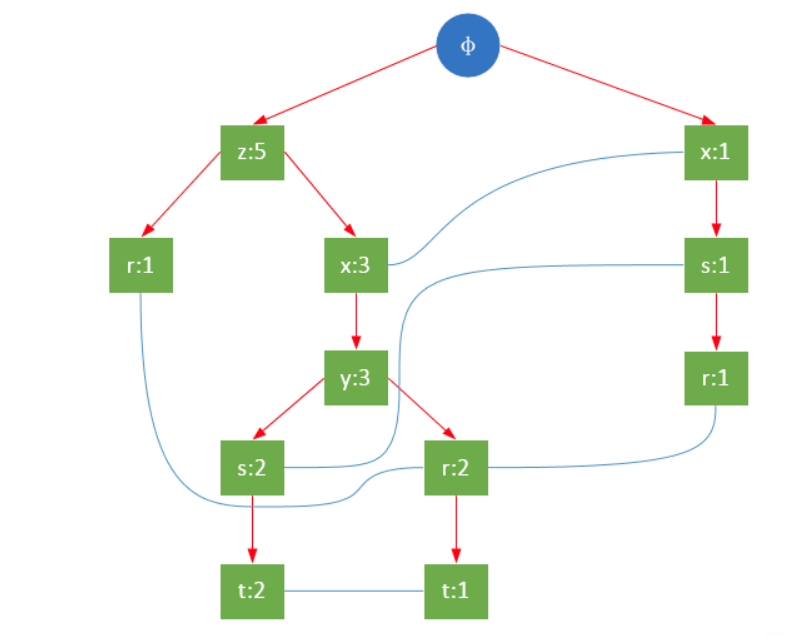
通常,FP树的大小比未压缩的数据小,因为数据的事务常常共享一些共同项,在最好的情况下,所有的事务都具有相同的项集,FP树只包含一条节点路径;当每个事务都具有唯一项集时,导致最坏情况发生,由于事务不包含任何共同项,FP树的大小实际上与原数据的大小一样。
FP树的根节点用φ表示,其余节点包括一个数据项和该数据项在本路径上的支持度;每条路径都是一条训练数据中满足最小支持度的数据项集;FP树还将所有相同项连接成链表,上图中用蓝色连线表示。
为了快速访问树中的相同项,还需要维护一个连接具有相同项的节点的指针列表(headTable),每个列表元素包括:数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针。
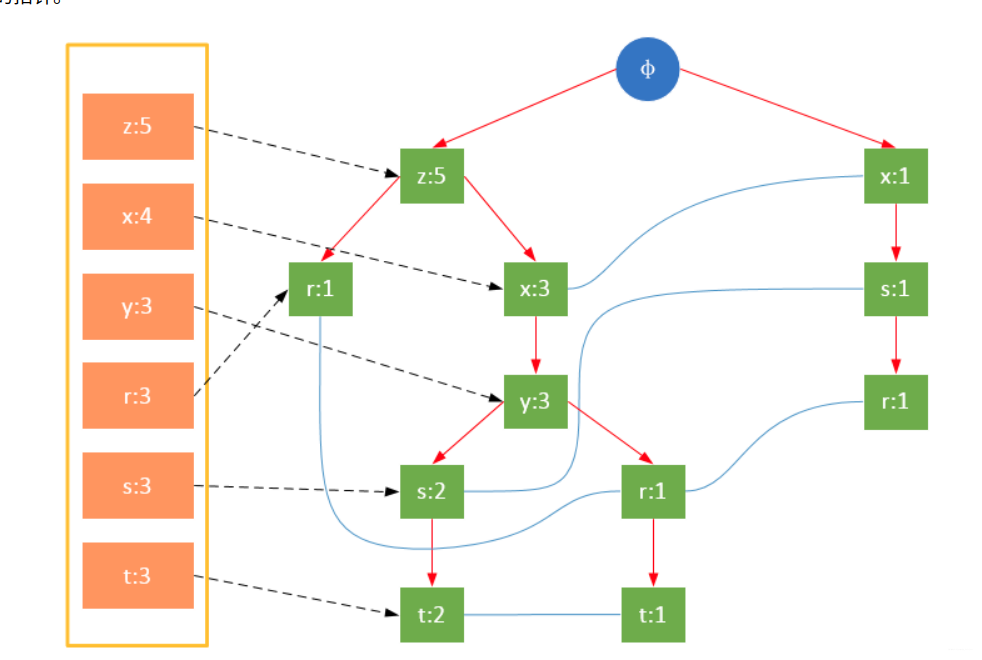
构建FP树
现在有如下数据:
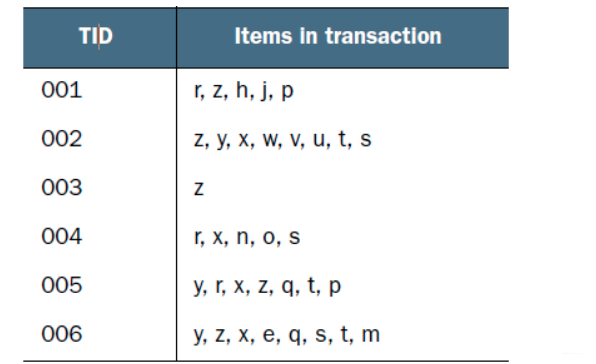
FP-growth算法需要对原始训练集扫描两遍以构建FP树。
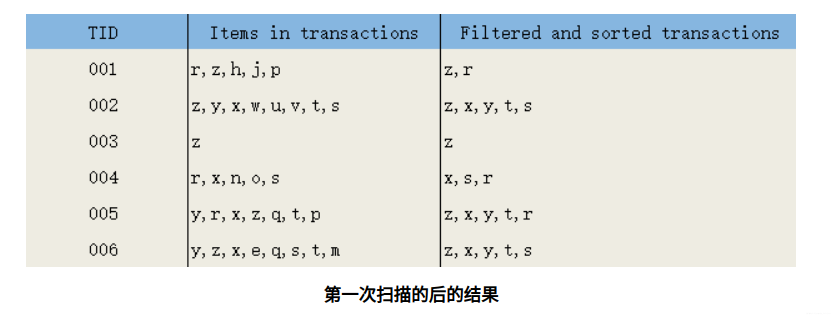
第一次扫描,过滤掉所有不满足最小支持度的项;对于满足最小支持度的项,按照全局最小支持度排序,在此基础上,为了处理方便,也可以按照项的关键字再次排序。
第二次扫描,构造FP树。
参与扫描的是过滤后的数据,如果某个数据项是第一次遇到,则创建该节点,并在headTable中添加一个指向该节点的指针;否则按路径找到该项对应的节点,修改节点信息。具体过程如下所示:
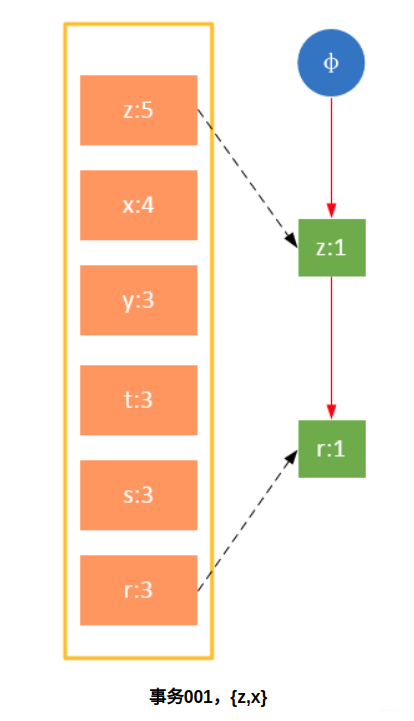
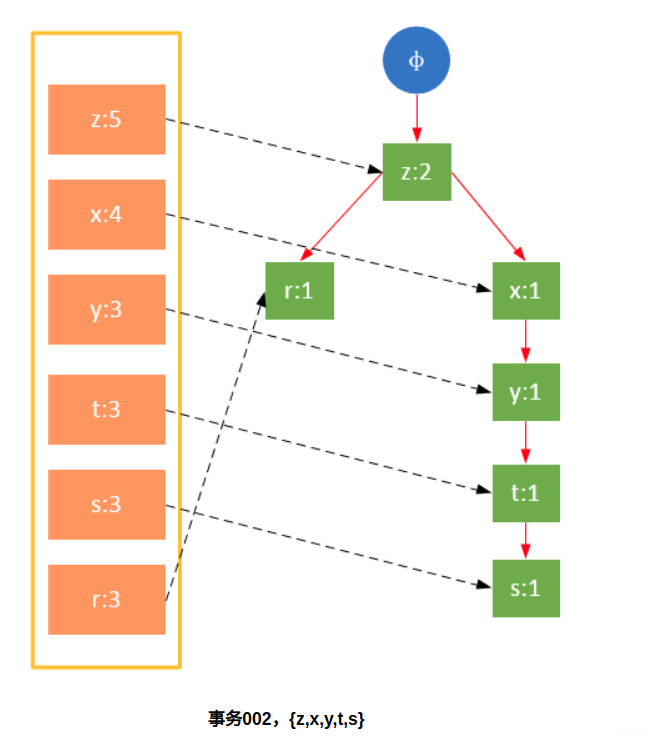
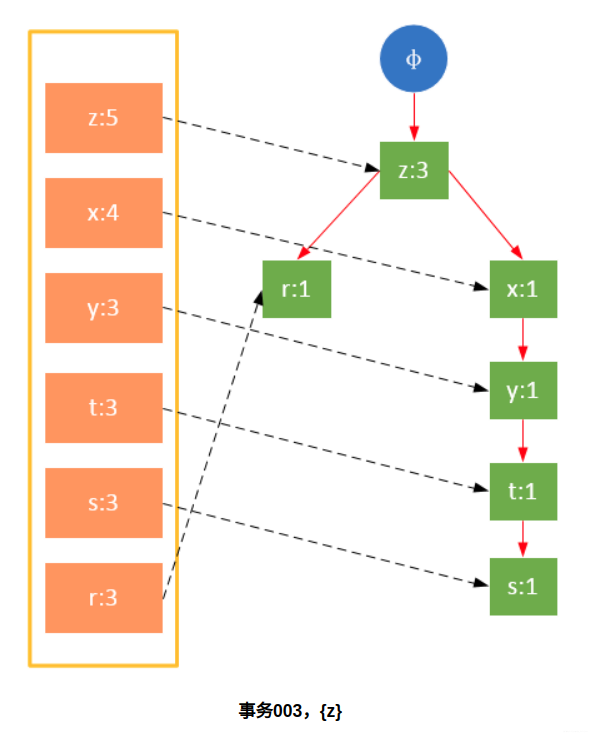
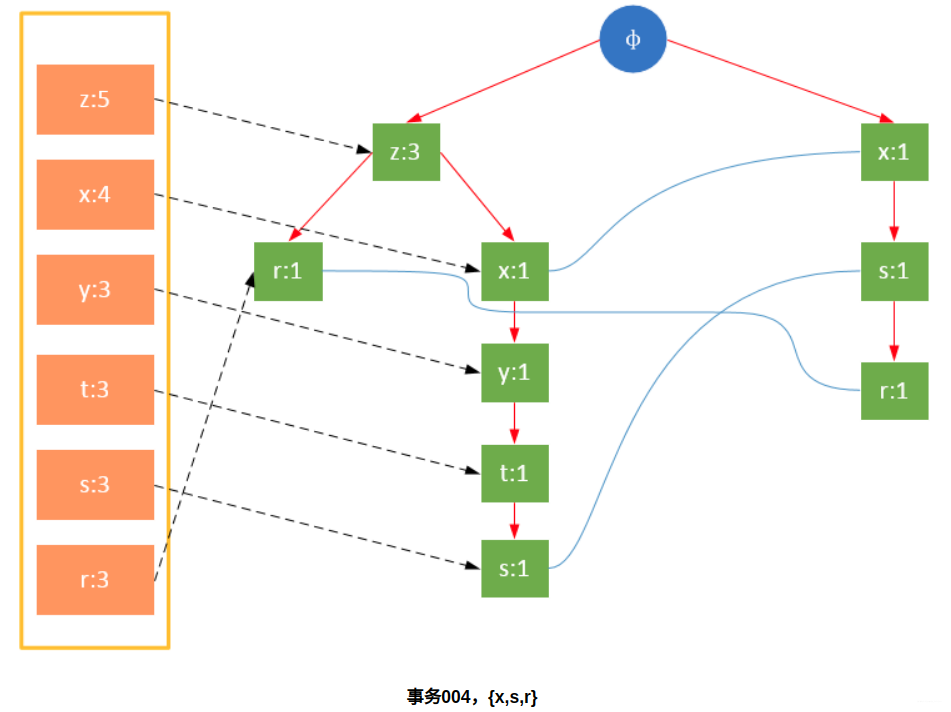
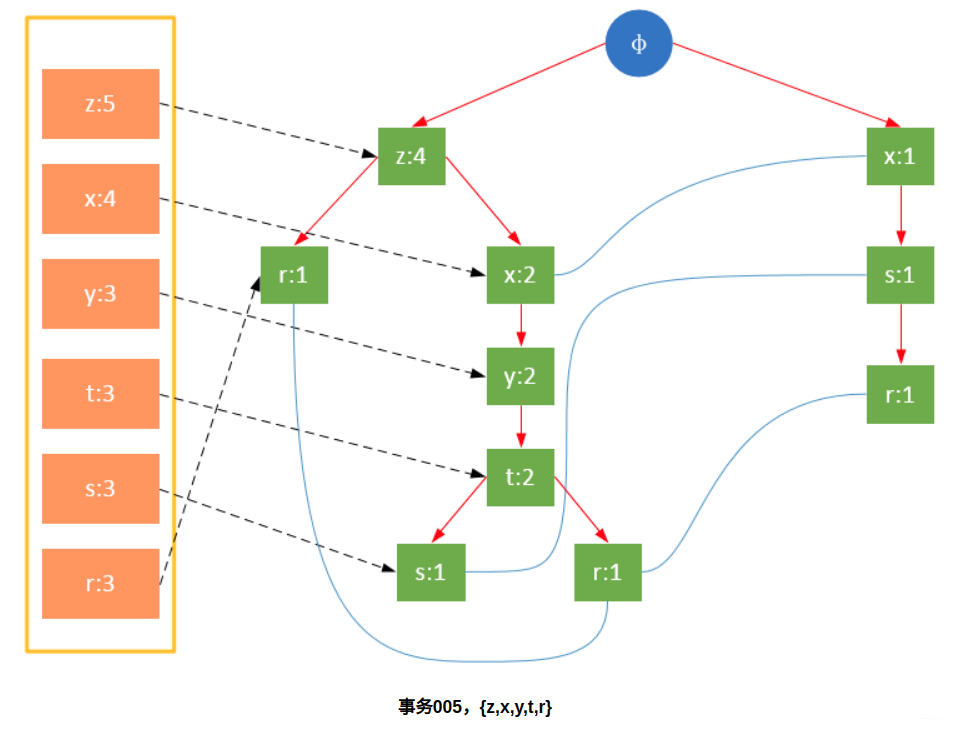
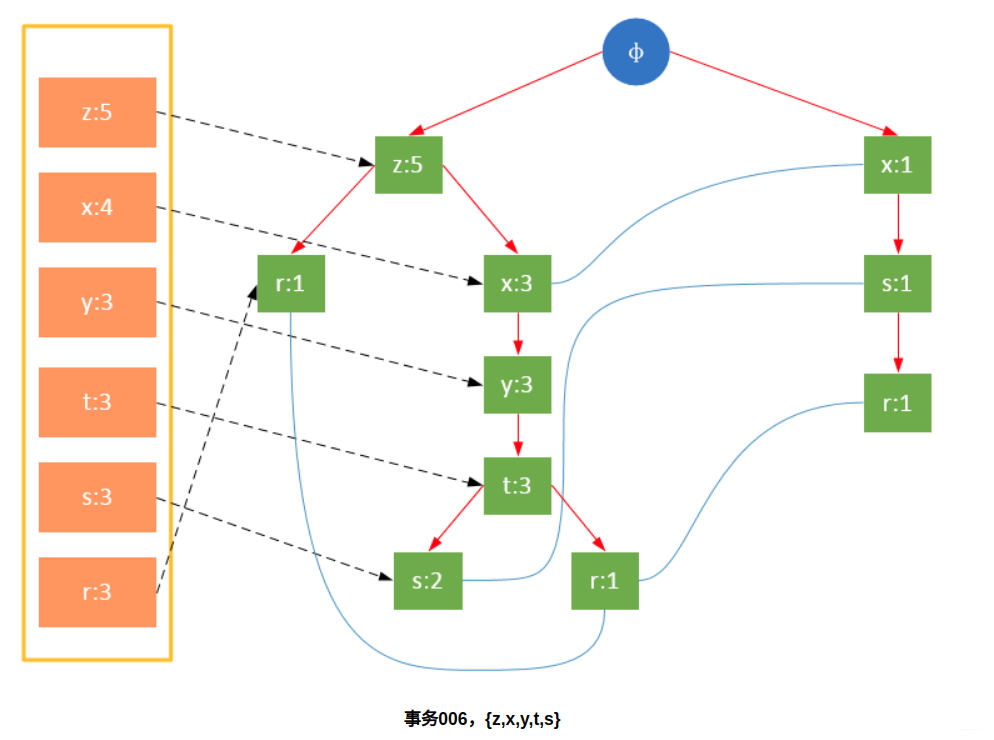
从上面可以看出,headTable并不是随着FPTree一起创建,而是在第一次扫描时就已经创建完毕,在创建FPTree时只需要将指针指向相应节点即可。从事务004开始,需要创建节点间的连接,使不同路径上的相同项连接成链表。
实现代码
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDatdef createInitSet(dataSet):retDict = {}for trans in dataSet:fset = frozenset(trans)retDict.setdefault(fset, 0)retDict[fset] += 1return retDictclass treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccurself.nodeLink = Noneself.parent = parentNodeself.children = {}def inc(self, numOccur):self.count += numOccurdef disp(self, ind=1):print(' ' * ind, self.name, ' ', self.count)for child in self.children.values():child.disp(ind + 1)def createTree(dataSet, minSup=1):headerTable = {}#此一次遍历数据集, 记录每个数据项的支持度for trans in dataSet:for item in trans:headerTable[item] = headerTable.get(item, 0) + 1#根据最小支持度过滤lessThanMinsup = list(filter(lambda k:headerTable[k] < minSup, headerTable.keys()))for k in lessThanMinsup: del(headerTable[k])freqItemSet = set(headerTable.keys())#如果所有数据都不满足最小支持度,返回None, Noneif len(freqItemSet) == 0:return None, Nonefor k in headerTable:headerTable[k] = [headerTable[k], None]retTree = treeNode('φ', 1, None)#第二次遍历数据集,构建fp-treefor tranSet, count in dataSet.items():#根据最小支持度处理一条训练样本,key:样本中的一个样例,value:该样例的的全局支持度localD = {}for item in tranSet:if item in freqItemSet:localD[item] = headerTable[item][0]if len(localD) > 0:#根据全局频繁项对每个事务中的数据进行排序,等价于 order by p[1] desc, p[0] descorderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: (p[1],p[0]), reverse=True)]updateTree(orderedItems, retTree, headerTable, count)return retTree, headerTabledef updateTree(items, inTree, headerTable, count):if items[0] in inTree.children: # check if orderedItems[0] in retTree.childreninTree.children[items[0]].inc(count) # incrament countelse: # add items[0] to inTree.childreninTree.children[items[0]] = treeNode(items[0], count, inTree)if headerTable[items[0]][1] == None: # update header tableheaderTable[items[0]][1] = inTree.children[items[0]]else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]])if len(items) > 1: # call updateTree() with remaining ordered itemsupdateTree(items[1:], inTree.children[items[0]], headerTable, count)def updateHeader(nodeToTest, targetNode): # this version does not use recursionwhile (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list!nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNodesimpDat = loadSimpDat()
dictDat = createInitSet(simpDat)
myFPTree,myheader = createTree(dictDat, 3)
myFPTree.disp()
上面的代码在第一次扫描后并没有将每条训练数据过滤后的项排序,而是将排序放在了第二次扫描时,这可以简化代码的复杂度。
控制台信息:

建模资料
资料分享: 最强建模资料


相关文章:

2023年高教社杯数学建模思路 - 案例:FPTree-频繁模式树算法
文章目录 算法介绍FP树表示法构建FP树实现代码 建模资料 ## 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,…...

批量根据excel数据绘制饼状图
要使用Python批量根据Excel数据绘制饼状图,可以使用pandas和matplotlib库来实现。以下是一个基本的代码示例: import pandas as pd import matplotlib.pyplot as plt # 读取Excel文件 data pd.read_excel(data.xlsx) # 提取需要用于绘制饼状图的数据列…...

C++头文件和std命名空间
C 是在C语言的基础上开发的,早期的 C 还不完善,不支持命名空间,没有自己的编译器,而是将 C 代码翻译成C代码,再通过C编译器完成编译。 这个时候的 C 仍然在使用C语言的库,stdio.h、stdlib.h、string.h 等头…...

浏览器有哪几种缓存?各种缓存之间的优先级
在浏览器中,有以下几种常见的缓存: 1、强制缓存:通过设置 Cache-Control 和 Expires 等响应头实现,可以让浏览器直接从本地缓存中读取资源而不发起请求。2、协商缓存:通过设置 Last-Modified 和 ETag 等响应头实现&am…...
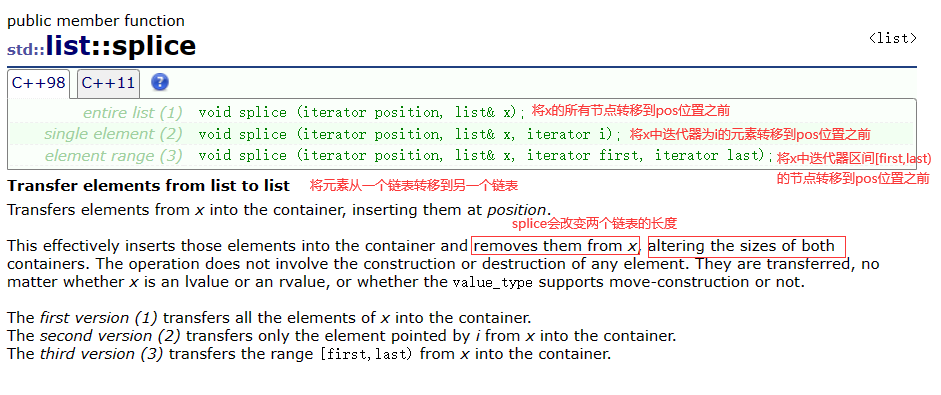
【C++】list
list 1. 简单了解list2. list的常见接口3. 简单实现list4. vector和list比较 1. 简单了解list list的底层是带头双向循环列表。因此list支持任意位置的插入和删除,且效率较高。但其缺陷也很明显,由于各节点在物理空间是不连续的,所以不支持对…...

剪枝基础与实战(2): L1和L2正则化及BatchNormalization讲解
1. CIFAR10 数据集 CIFAR10 是深度学习入门最先接触到的数据集之一,主要用于图像分类任务中,该数据集总共有10个类别。 图片数量:6w 张图片宽高:32x32图片类别:10Trainset: 5w 张,5 个训练块Testset: 1w 张,1 个测试块Pytorch 集成了很多常见数据集的API, 可以通过py…...

C语言学习笔记---指针进阶01
C语言程序设计笔记---016 C语言指针进阶前篇1、字符指针2、指针数组2.1、指针数组例程1 -- 模拟一个二维数组2.2、指针数组例程2 3、数组指针3.1、回顾数组名?3.2、数组指针定义与初始化(格式)3.3、数组指针的作用 --- 常用于二维数组3.4、数…...

【Go 基础篇】Go 语言字符串函数详解:处理字符串进阶
大家好!继续我们关于Go语言中字符串函数的探索。字符串是编程中常用的数据类型,而Go语言为我们提供了一系列实用的字符串函数,方便我们进行各种操作,如查找、截取、替换等。在上一篇博客的基础上,我们将继续介绍更多字…...

GAN原理 代码解读
模型架构 代码 数据准备 import os import time import matplotlib.pyplot as plt import numpy as np import torchvision.transforms as transforms from torch.utils.data import DataLoader from torchvision import datasets import torch.nn as nn import torch# 创建文…...
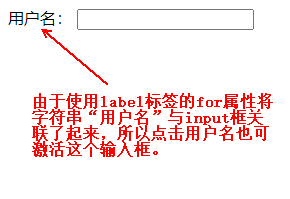
HTML的label标签有什么用?
当你想要将表单元素(如输入框、复选框、单选按钮等)与其描述文本关联起来,以便提供更好的用户界面和可访问性时,就可以使用HTML中的<label>标签。<label>标签用于为表单元素提供标签或标识,使用户能够更清…...
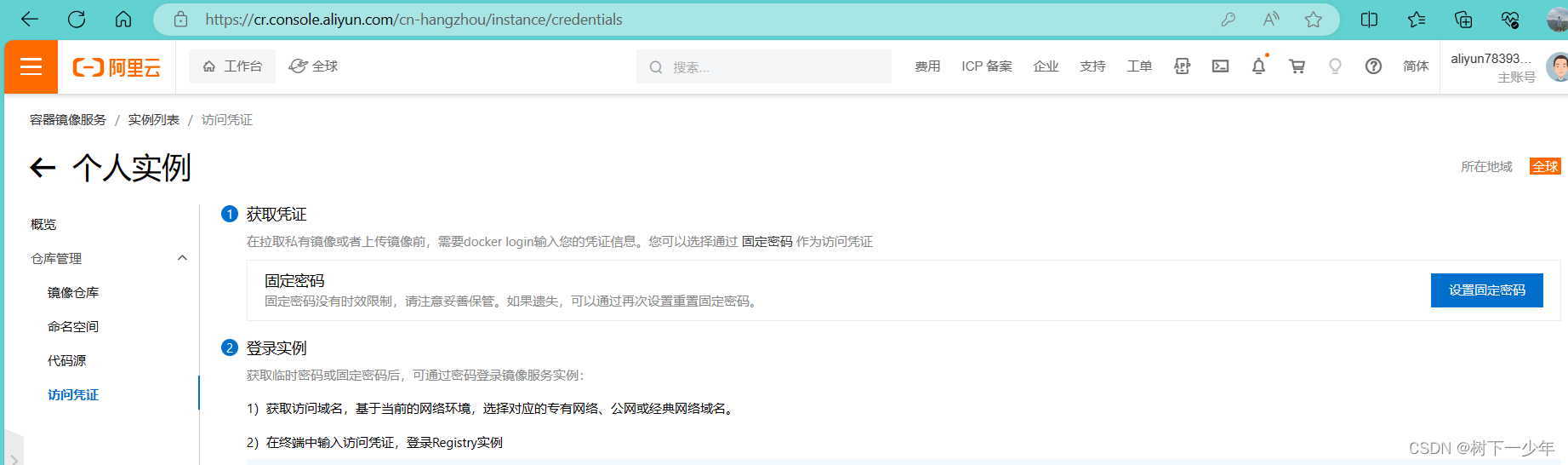
docker在阿里云上的镜像仓库管理
目录 一.登录进入阿里云网站,点击个人实例进行创建 二.创建仓库,填写相关信息 三.在访问凭证中设置固定密码用于登录,登录时用户名是使用你注册阿里云的账号名称,密码使用设置的固定密码 四.为镜像打标签并推送到仓库 五.拉取…...

html-dom核心内容--四要素
1、结构 HTML DOM (文档对象模型) 当网页被加载时,浏览器会创建页面的文档对象模型(Document Object Model)。 2、核心关注的内容:“元素”,“属性”,“修改样式”,“事件反应”。>四要素…...

golang的继承
golang中并没有继承以及oop,但是我们可以通过struct嵌套来完成这个操作。 定义struct 以下定义了一个Person结构体,这个结构体有Eat方法以及三个属性 type Person struct {Name stringAge uint16Phone string }func (recv *Person) Eat() {fmt.Prin…...

Google Play商店优化排名因素之应用截图与视频
屏幕截图是影响转化率的最重要的视觉效果之一。大多数人只需查看应用程序屏幕截图,就会决定是否尝试去下载我们的应用程序。 1、在Google Play商店中,搜索结果页面根据我们搜索的关键词有不同的样式。 展示应用程序中最好的部分,添加一些文字…...

fastadmin iis伪静态应用入口文件index.php
<?xml version"1.0" encoding"UTF-8"?> <configuration><system.webServer><rewrite><rules><rule name"OrgPage" stopProcessing"true"><match url"^(.*)$" /><conditions…...
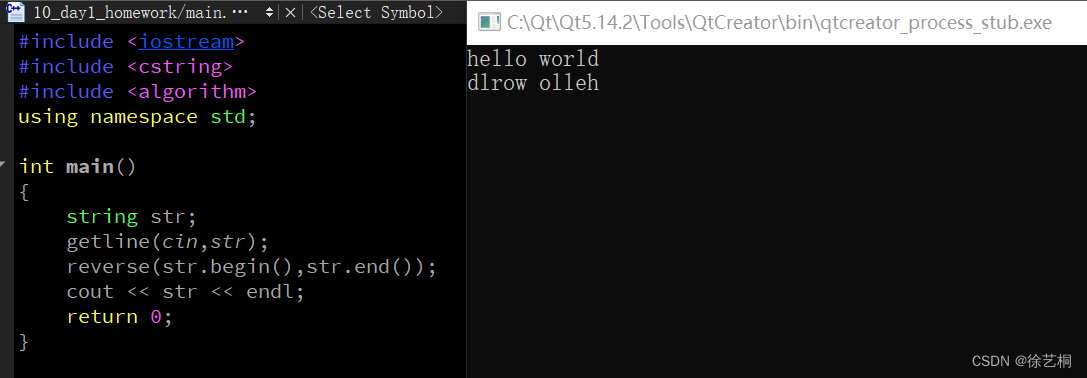
0821|C++day1 初步认识C++
一、思维导图 二、知识点回顾 【1】QT软件的使用 1)创建文件 创建文件时,文件的路径一定是全英文 2)修改编码 工具--->选项--->行为--->默认编码:system 【2】C和C的区别 C又叫C plus plus,C是对C的扩充&…...

Linux上实现分片压缩及解压分片zip压缩包 - 及zip、unzip命令详解
👨🎓博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 🐋 希望大家多多支…...

概率论作业啊啊啊
1 数据位置 (Measures of location) 对于数据集: 7 , 9 , 9 , 10 , 10 , 11 , 11 , 12 , 12 , 12 , 13 , 14 , 14 , 15 , 16 7,9,9,10,10,11,11,12,12,12,13,14,14,15,16 7,9,9,10,10,11,11,12,12,12,13,14,14,15,16 计算加权平均数,其中权重为: 2 , 1 , 3 , 2 ,…...

React re-render
What is? react的渲染分为两个阶段: render,组件第一次出现在屏幕上的时候触发re-render, 组件第一次渲染之后的渲染 当app的数据更新时(用户手动更新、或异步请求)。 When? re-render发生有四种可能: state改变…...
从零开始配置Jenkins与GitLab集成:一步步实现持续集成
在软件开发中,持续集成是确保高效协作和可靠交付的核心实践。以下是在CentOS上安装配置Jenkins与GitLab集成的详细步骤: 1.安装JDK 解压JDK安装包并设置环境变量: JDK下载网址 Java Downloads | Oracle 台灣 tar zxvf jdk-11.0.5_linux-x64_b…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...
