转置卷积的应用
目录
矩阵转置
一、转置卷积的背景
二、转置卷积的应用
三、转置卷积的区别
卷积
矩阵转置

矩阵的转置在信息处理中起到了重要的作用。在计算机科学领域,矩阵常用于表示图像、音频和视频等多媒体数据。当我们需要对这些数据进行处理时,常常需要进行矩阵转置操作。例如,在图像处理中,我们往往需要将图像矩阵进行转置来实现旋转、镜像等效果。在音频处理中,矩阵转置可以用于音频信号的变换和滤波等操作。因此,矩阵的转置在信息处理中具有重要的现实意义
知阵的转置在数据分析中也非常常见。在统计学和机器学习领域,短阵常用于表示样本数据和特征向量。通过对短阵进行转置,我们可以改变数据的排列方式,使得不同的变量或属性可以更好地进行比较和分析。例如,在多元统计分析中,矩阵的转置可以用于求解特征值和特征向量,进而得到数据的主成分和相关性。此外,在数据挖掘和预测分析中,短阵的转置也可以用于特征选择和模型建立等关键步骤。因此,短阵的转置在数据分析中具有重要的现实意义。
矩阵的转置在计算机图形学中也有看广泛的应用。在三维图形的表示和变换中,短阵常用于描述物体的位置、旋转和缩放等变换。通过对矩阵进行转置,我们可以方便地实现不同坐标系之间的转换和变换。例如,在计算机动画中,矩阵的转置可以用于实现物体的运动和变形效果。
一、转置卷积的背景
通常,对图像进行多次卷积运算后,特征图的尺寸会不断缩小。而对于某些特定任务 (如 图像分割 和 图像生成 等),需将图像恢复到原尺寸再操作。这个将图像由小分辨率映射到大分辨率的尺寸恢复操作,叫做 上采样 (Upsample):
上采样方法有很多,最近邻插值、线性插值、双线性插值、双三次插值。然而,这些上采样方法都是基于人们的先验经验来设计的,在很多场景中效果并不理想 (如 规则固定、不可学习)。
二、转置卷积的应用
曾经,转置卷积 又称 反卷积 (Deconvolution)。与传统的上采样方法相比,转置卷积的上采样方式 并非预设的插值方法,而是同标准卷积一样,具有可学习的参数,可通过网络学习来获取最优的上采样方式。
转置卷积 在某些特定领域具有广泛应用,比如:
在 DCGAN,生成器将随机值转变为一个全尺寸图片,此时需用到转置卷积。
在语义分割中,会在编码器中用卷积层提取特征,然后在解码器中恢复原先尺寸,从而对原图中的每个像素分类。该过程同样需用转置卷积。经典方法有 FCN 和 U-Net。
CNN 可视化:通过转置卷积将 CNN 的特征图还原到像素空间,以观察特定特征图对哪些模式的图像敏感。
三、转置卷积的区别
标准卷积的运算操作 其实是对卷积核中的元素 与输入矩阵上对应位置的元素 进行逐像素的乘积并求和。然后,卷积核在输入矩阵上以步长为单位进行滑动,直到遍历完输入矩阵的所有位置。
假设,输入是一个 4×4 矩阵,使用 3×3 的标准卷积进行计算,同时令 padding=0,stride=1。最终输出结果应是一个 2×2 矩阵,如图 2 所示: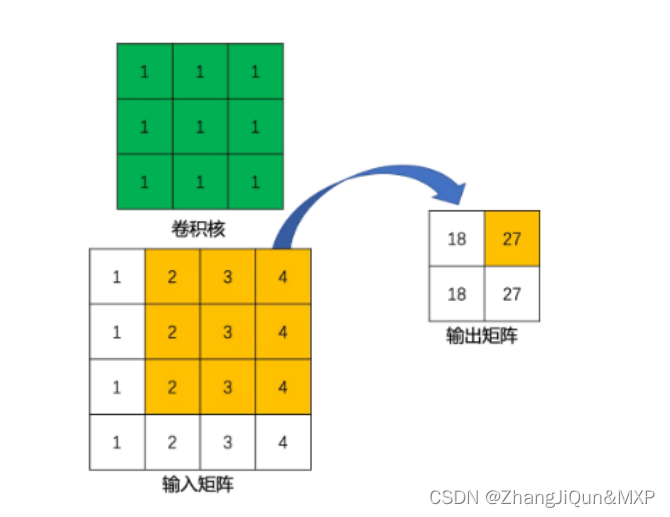
在上例中,输入矩阵右上角 3×3 范围的值 (黄色 2 3 4) 会影响 输出矩阵右上角的值 (黄色 27),这其实也对应了标准卷积中感受野的概念。所以,可以说 3×3 标准卷积核 建立了 输入矩阵中 9 个值 到 输出矩阵中 1 个值 的映射关系。
综上所述,我们也就可以认为标准卷积操作实际上就是建立了一个 多对一的映射关系。
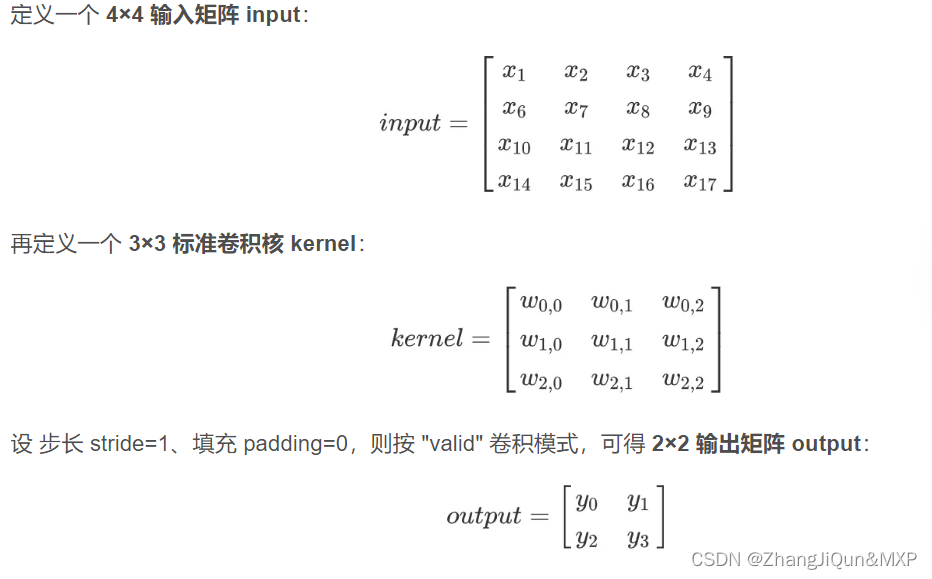
对转置卷积而言,我们实际上是想建立一个逆向操作,即 一对多的映射关系。对于上例,我们想要建立的其实是输出矩阵中的 1 个值与输入矩阵中的 9 个值的关系,如图 3 所示:

当然,从信息论的角度上看,常规卷积操作是不可逆的,所以转置卷积并不是通过输出矩阵和卷积核计算原始输入矩阵,而是计算得到保持了相对位置关系的矩阵。
六、小结
注意:矩阵中的实际权值不一定来自原始卷积矩阵。重要的是权重的排布是由卷积矩阵的转置得来的。转置卷积运算与普通卷积形成相同的连通性,但方向是反向的。
我们可以用转置卷积来上采样,而 转置卷积的权值是可学习的,所以无需一个预定义的插值方法。
尽管它被称为转置卷积,但这并不意味着我们取某个已有的卷积矩阵并使用转置后的版本。重点是,与标准卷积矩阵 (一对多关联而不是多对一关联) 相比,输入和输出之间的关联是以反向的方式处理的
因此,转置卷积不是卷积,但可以用卷积来模拟转置卷积。通过在输入矩阵的值间插入零值 (以及周围填零) 上采样输入矩阵,然后进行常规卷积 就会产生 与转置卷积相同的效果。你可能会发现一些文章用这种方式解释了转置卷积。但是,由于需要在常规卷积前对输入进行上采样,所以效率较低。
注意:转置卷积会导致生成图像中出现 网格/棋盘效应 (checkerboard artifacts),因此后续也存在许多针对该问题的改进工作。
卷积
对于一个输入 的图像,不考虑通道的维度,卷积核的大小为 ,步长为 1,填充为 0。


相关文章:

转置卷积的应用
目录 矩阵转置 一、转置卷积的背景 二、转置卷积的应用 三、转置卷积的区别 卷积 矩阵转置 矩阵的转置在信息处理中起到了重要的作用。在计算机科学领域,矩阵常用于表示图像、音频和视频等多媒体数据。当我们需要对这些数据进行处理时,常常需要进行…...

常见的移动端布局
流式布局(百分比布局) 使用百分比、相对单位(如 em、rem)等来设置元素的宽度,使页面元素根据视口大小的变化进行调整。这种方法可以实现基本的自适应效果,但可能在不同设备上显示不一致。 <!DOCTYPE ht…...
Typore 亲测有效(懂得都懂哈)
Typore 亲测从安装到使用,可以使用(具体是什么懂得都懂哈) 网盘下载地址:链接:https://pan.baidu.com/s/1w0UiS1szxnO9Lxz6sbXEKg?pwdqwe1 提取码:qwe1 第一步: 下载压缩包进行解压,解压过…...

Kyligence Copilot 登陆海外,斩获 Product Hunt 日榜 TOP 2
8月14日,AI 数智助理 Kyligence Copilot 在全球知名科技产品平台 Product Hunt 上线,其以出色的产品创新实力,在激烈的竞争中脱颖而出,仅仅在 24 小时内收获了超过 400 个投票和近 200 条支持评论,荣登当日产品榜排名第…...

【Docker】Docker 的基本概念和优势,基本命令及使用例子
Docker 是一种轻量级的容器化解决方案,能够快速地创建、部署和运行应用程序。以下是一些 Docker 的基本概念和优势: 基本概念: 1.镜像:一个 Docker 镜像是一个可执行的文件,其中包含了运行应用程序所需要的一切。 2.容…...
[4])
高并发内存池(回收)[4]
threadcache还给centralcache void ThreadCache::Deallocate(void* ptr, size_t size) {assert(ptr);assert(size < MAX_BYTES);// 找对映射的自由链表桶,对象插入进入size_t index SizeClass::Index(size);_freeLists[index].Push(ptr);// 当链表长度大于一次…...
分布式事务篇-2.4 Spring-Boot整合Seata
文章目录 前言一、pom jar导入:二、项目配置:2.1 配置 说明:2.1 .1 seata server 端:2.1 .2 seata client 端: 2.2 开启seata 对于数据源的代理:2.3 seata-client 的注册中心:2.4 seata-client 的配置中心:2.5 去掉手写的数据源代…...

718. 最长重复子数组
718. 最长重复子数组 原题链接:完成情况:题解:方法一:动态规划方法二:滑动窗口方法三:二分查找 哈希 原题链接: 718. 最长重复子数组 https://leetcode.cn/problems/maximum-length-of-repe…...

Mysql join加多条件与where的区别
最近在项目中遇到一个问题,感觉有点意思,在解决问题及查阅了相关资料后,打算写篇文章给朋友们分享一下。 问题现象: 问题是很常见的空指针问题,后端查询数据库数据,遍历进行相关业务处理时报空指针。通过…...

div滚动条自动滚动到底部
<div id"center"></div>// 滚动条到最底部scrollToBottom(){var box document.getElementById(center);this.$nextTick(() > {box.scrollTop box.scrollHeight})},...
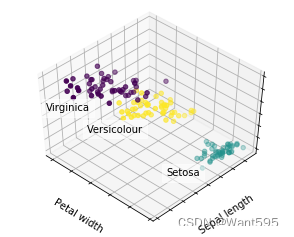
【深度学习】实验02 鸢尾花数据集分析
文章目录 鸢尾花数据集分析决策树K-means 鸢尾花数据集分析 决策树 # 导入机器学习相关库 from sklearn import datasets from sklearn import treeimport matplotlib.pyplot as plt import numpy as np# Iris数据集是常用的分类实验数据集, # 由Fisher, 1936收集…...

AI大模型潮水中,医疗数字化加速「求解」
蝴蝶挥动翅膀,医疗行业每个角落开始连锁反应,曾经被忽视的问题也愈发明显。但与之对应的是,对数字化和AI大模型的价值认可,在中国医疗赛道也正在加速来临。 作者|斗斗 编辑|皮爷 出品|产业家 重庆市某地方人民医院…...
【安卓】自定义View实现画板涂鸦等功能
一、实现效果 二、代码 1、MainActivity.class package com.lsl.mydrawingboarddemo;import androidx.appcompat.app.AppCompatActivity; import androidx.core.content.ContextCompat;import android.os.Bundle; import android.os.Handler; import android.view.View; impo…...

面试题. 搜索旋转数组
搜索旋转数组。给定一个排序后的数组,包含n个整数,但这个数组已被旋转过很多次了,次数不详。请编写代码找出数组中的某个元素,假设数组元素原先是按升序排列的。若有多个相同元素,返回索引值最小的一个。 示例1: 输入…...
前端需要理解的数据治理与异常监控知识
1 数据治理 前端数据治理的重要指标是准确性和数据,一个数据对象包括数据值和其他元数据。 2 数据上报方式 2.1 Image 通过将采集的数据拼接在图片请求的后面,向服务端请求一个 1*1 px 大小的图片(gif)实现的,设置…...
hook 后的开始 一)
ip_vs 原理解析 (四)hook 后的开始 一
文章目录 ip_vs hook 后NF_INET_LOCAL_IN 本章重点: k8s 如何利用 ip_vs 实现源 IP 会话亲和性。 ip_vs hook 后 NF_INET_LOCAL_IN 根据优先级依次是 ip_vs_reply4,ip_vs_remote_request4 ip_vs_reply4| -- ip_vs_out| -- skb_to_full_sk(skb…...
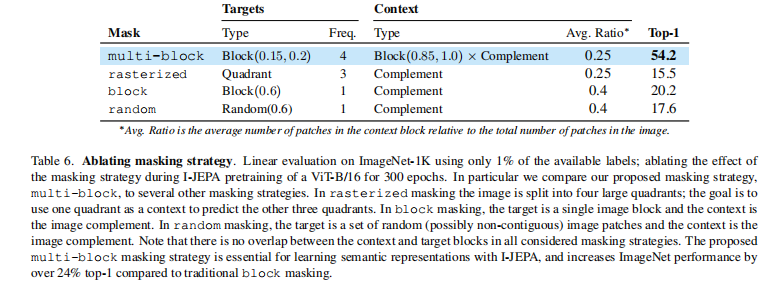
【论文解读】基于图的自监督学习联合嵌入预测架构
一、简要介绍 本文演示了一种学习高度语义的图像表示的方法,而不依赖于手工制作的数据增强。论文介绍了基于图像的联合嵌入预测架构(I-JEPA),这是一种用于从图像中进行自监督学习的非生成性方法。I-JEPA背后的idea很简单ÿ…...

C++ 容器
string 1. 构造 string s1(); // 1 string s2("hello"); // hello string s3(3, k); // kkk string s4("hellohello", 2, 4); // lloh2. 赋值 string s1 "hellohello"; // hellohello string s2.assign(s1); // he…...

【PHP】PHP文件操作详解
PHP是一种广泛使用的服务器端脚本语言,用于开发Web应用程序。在PHP中,文件操作是一项重要的功能,包括文件的读取、写入、删除和其他操作。本文将详细介绍PHP文件操作的各个方面,并通过示例代码进行说明。 一、文件读取 要读取一…...

硬核旗舰南卡OE CC开放式耳机发布,重新定义百元开放式耳机新标杆!
随着现在健康意识的不断提高,人们对于日常用品的要求越来越高,在耳机市场中,健康因素也逐渐成为消费者所考虑的因素之一,入耳式耳机因为会引发中耳炎、耳膜炎等疾病,正在逐渐被开放式蓝牙耳机所取代,南卡…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...
