c 语言 算法 技巧 之 用移位来代替乘除
除法
当你需要计算一个数的一半时,通常我们会考虑使用除法运算(/)来实现。然而,计算机内部的运算中,除法通常比加法和乘法运算慢得多,因为除法需要更多的处理步骤。
位运算在这种情况下可以提供一个快速的替代方案,特别是当你要计算一个整数的一半,或者是进行类似的整除操作。这是因为向右移动二进制位相当于将数值除以2的幂。
例如,假设你有一个整数 x,你想计算它的一半。使用除法运算,你会这样做:
int half = x / 2;
然而,使用位运算的右移操作,你可以这样做:
int half = x >> 1;
这两个操作实际上是等价的,但是位运算操作更快,因为计算机底层的硬件可以直接对二进制位进行操作。
当然,这个技巧不仅仅适用于除以2。如果你想进行除以2的幂次方的整数除法(例如除以4、8、16等),你可以通过多次右移操作来实现。例如:
int quarter = x >> 2; // 相当于 x / 4
int eighth = x >> 3; // 相当于 x / 8
需要注意的是,这个技巧只适用于正整数或者无符号整数。对于负数,右移操作的行为是取决于编译器和平台的,可能会产生不一致的结果。
总之,位运算技巧可以用来加速整数的一些数值操作,特别是涉及除以2的操作,以及除以2的幂次方。但在使用时,应该注意代码的可读性和可维护性,以确保你的代码仍然清晰易懂。
乘法
对于乘法,也有一些位运算的技巧可以用来加速一些特定情况下的乘法操作。这些技巧通常适用于乘以2的幂次方或者相关的操作。
乘以2的幂次方: 乘以2的幂次方可以通过左移位运算(<<)来实现。左移一位相当于乘以2,左移两位相当于乘以4,以此类推。例如:
int multipliedByTwo = x << 1; // 相当于 x * 2
int multipliedByFour = x << 2; // 相当于 x * 4
乘以其他整数: 对于乘以其他整数,位运算并不一定能提供明显的优势,因为一般情况下乘法运算比位运算复杂。位运算主要适用于2的幂次方。
需要注意的是,对于乘法和位运算的优化,编译器和硬件在许多情况下会自动进行优化,所以在编写代码时,首要考虑的应该是代码的可读性和可维护性。只有在性能优化确实变得重要时,你才应该考虑使用这些技巧。
总之,位运算技巧可以在特定情况下用来加速乘法操作,尤其是与2的幂次方相关的操作。但是请务必谨慎使用,以免降低代码的可读性和可维护性。
相关文章:

c 语言 算法 技巧 之 用移位来代替乘除
除法 当你需要计算一个数的一半时,通常我们会考虑使用除法运算(/)来实现。然而,计算机内部的运算中,除法通常比加法和乘法运算慢得多,因为除法需要更多的处理步骤。 位运算在这种情况下可以提供一个快速的…...

python爬虫实战零基础(3)——某云音乐
爬取某些云网页音乐,无需app 分析网页第二种方式批量爬取 声明:仅供参考学习,参考,若有不足,欢迎指正 你是不是遇到过这种情况,在pc端上音乐无法下载,必须下载客户端才能下载? 那么&…...
渗透测试漏洞原理之---【XSS 跨站脚本攻击】
文章目录 1、跨站 脚本攻击1.1、漏洞描述1.2、漏洞原理1.3、漏洞危害1.4、漏洞验证1.5、漏洞分类1.5.1、反射性XSS1.5.2、存储型XSS1.5.3、DOM型XSS 2、XSS攻防2.1、XSS构造2.1.1、利用<>2.1.2、JavaScript伪协议2.1.3、时间响应 2.2、XSS变形方式2.2.1、大小写转换2.2.2…...

【浮点数二分】
数的三次方根 #include<iostream> using namespace std;double n;int main(){cin>>n;double l -10000;double r 10000;while((r-l)>1e-8){double mid (lr)/2;if((mid*mid*mid)>n) r mid;else l mid;}printf("%lf",l);return 0; }...
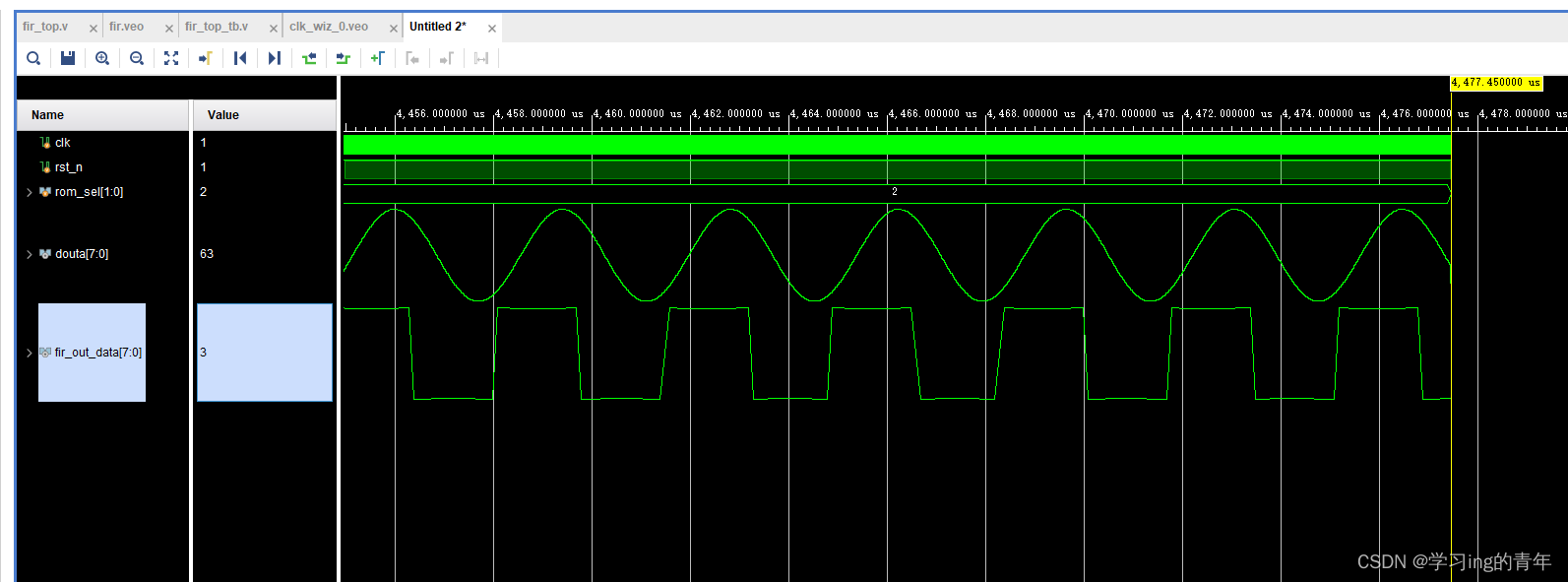
基于FPGA的FIR低通滤波器实现(附工程源码),matlab+vivado19.2+simulation
基于FPGA的FIR低通滤波器实现(附工程源码) 文章目录 基于FPGA的FIR低通滤波器实现(附工程源码)前言一、matlab设计FIR滤波器,生成正弦波1.设计FIR滤波器1.生成正弦波.coe 二、vivado1.fir滤波器IP核2.正弦波生成IP核3.时钟IP核设置4.顶层文件/测试文件代码 三.simul…...
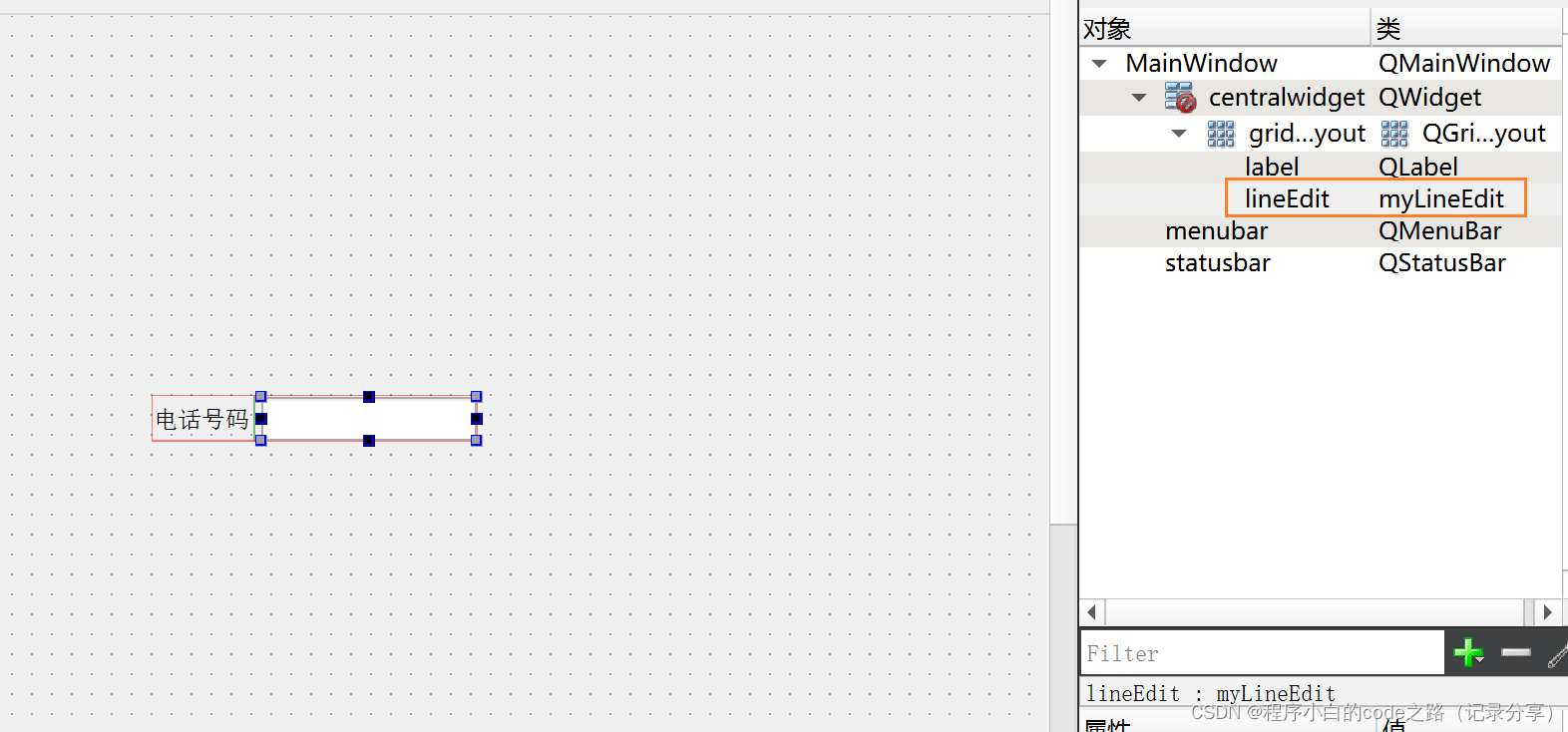
c++ qt--事件(第六部分)
c qt–事件(第六部分) 一.编辑伙伴,编辑顺序(按TAB进行切换) 1.编辑伙伴 此功能在设计界面如下的位置 1.设置伙伴关系 鼠标左键长按一个Label组件然后把鼠标移到另一个组件上 2.伙伴关系的作用 伙伴关系的作用就是…...
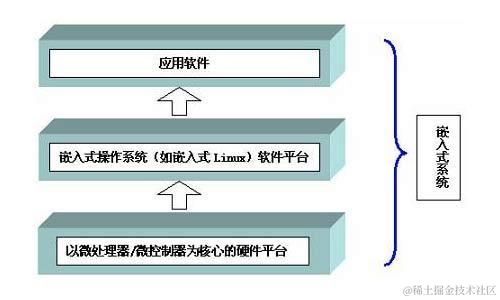
嵌入式系统入门实战:探索基本概念和应用领域
嵌入式系统是一种专用的计算机系统,它是为了满足特定任务而设计的。这些系统通常具有较低的硬件资源(如处理器速度、内存容量和存储容量),但具有较高的可靠性和实时性。嵌入式系统广泛应用于各种领域,如家用电器、汽车、工业控制、医疗设备等。 嵌入式系统的基本概念 微控…...

关于hive sql进行调优的理解
这是一个面试经常面的问题,很不幸,在没有准备的时候,我面到了这个题目,反思了下,将这部分的内容进行总结,给大家一点分享。 hive其实是基于hadoop的数据库管理工具,底层是基于MapReduce实现的&a…...

十大排序算法
一、冒泡排序 冒泡排序(Bubble Sort)是一种简单直观的排序算法。它重复地走访要排序的数列,一次比 较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经…...

PIP 常用操作汇总
1. 升级 python -m pip install --upgrade pip2. 列出所有安装包 pip list3. 查找特定包 pip list | findstr xxx4. 查看特定包 pip show xxx5. 安装软件包 pip install pyzmq24.0.16. 卸载软件包 pip uninstall -y pyzmq7. 查看配置 # 生效的配置(global -&…...

线性代数的本质笔记(3B1B课程)
文章目录 前言向量矩阵行列式线性方程非方阵点积叉积基变换特征向量与特征值抽象向量空间 前言 最近在复习线代,李永乐的基础课我刷了一下,感觉讲的不够透彻,和我当年学线代的感觉一样,就是不够形象。 比如,行列式为…...

快速掌握MQ消息中间件rabbitmq
快速掌握MQ消息中间件rabbitmq 目录概述需求: 设计思路实现思路分析1.video 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better result,wait for change,c…...

Git push拦截
遇到的问题 今天想提交代码到gitee,结果发现被拦截了,有段提示“forbidden by xxxx”… 我记得xxxx好像是公司的一个防泄密的东西… 这个东西是怎么实现的呢? 解决 原来git提供很多hook,push命令就有一个pre-push的hook&#x…...
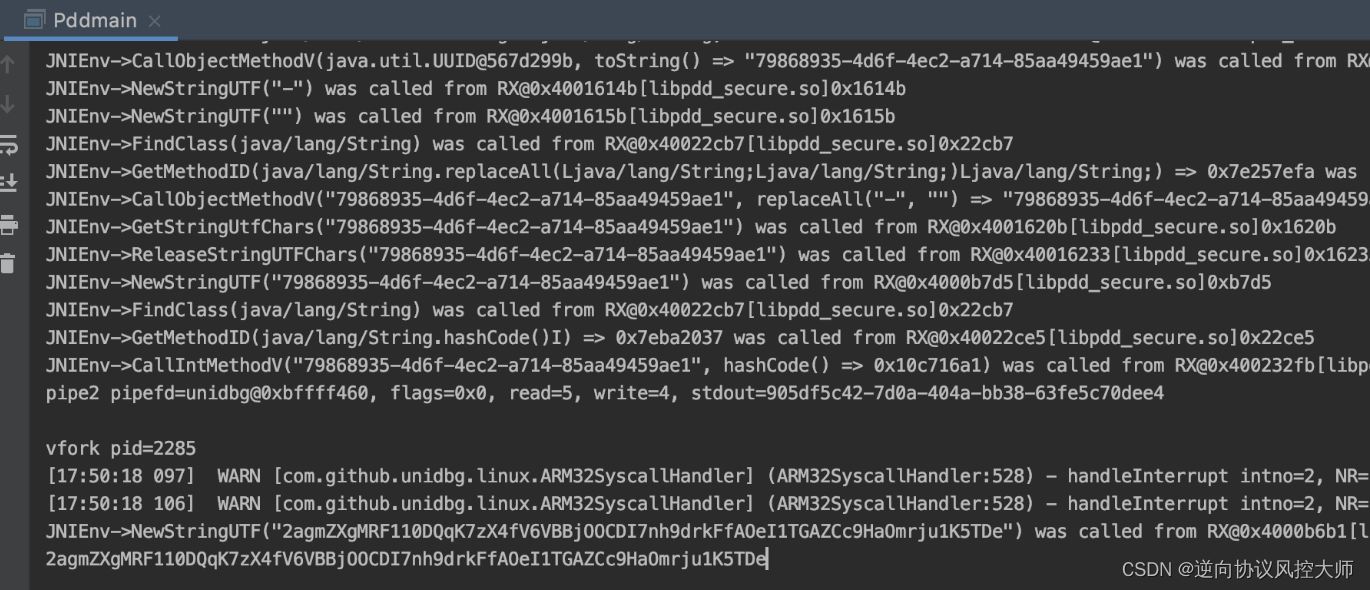
拼多多anti-token分析
前言:拼多多charles抓包分析发现跟商品相关的请求头里都带了一个anti-token的字段且每次都不一样,那么下面的操作就从分析anti-token开始了 1.jadx反编译直接搜索 选中跟http相关的类对这个方法进行打印堆栈 结合堆栈方法调用的情况找到具体anti-token是由拦截器类f…...
基于微信小程序的中医体质辨识文体活动的设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于微信小程序的中医体质辨识文体活动的设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java s…...
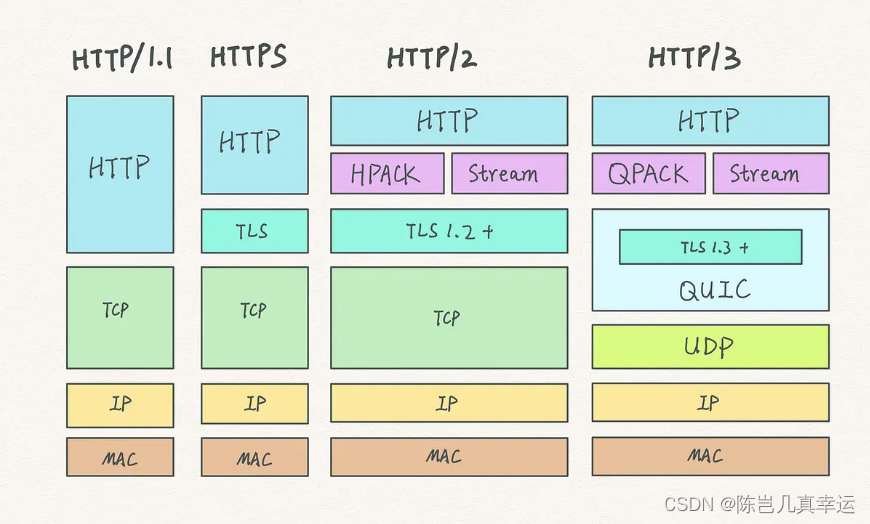
4.16 TCP 协议有什么缺陷?
目录 升级 TCP 的工作很困难 TCP 建立连接的延迟 TCP 存在队头阻塞问题 网络迁移需要重新建立 TCP 连接 升级 TCP 的工作很困难;TCP 建立连接的延迟;TCP 存在队头阻塞问题;网络迁移需要重新建立 TCP 连接; 升级 TCP 的工作很…...
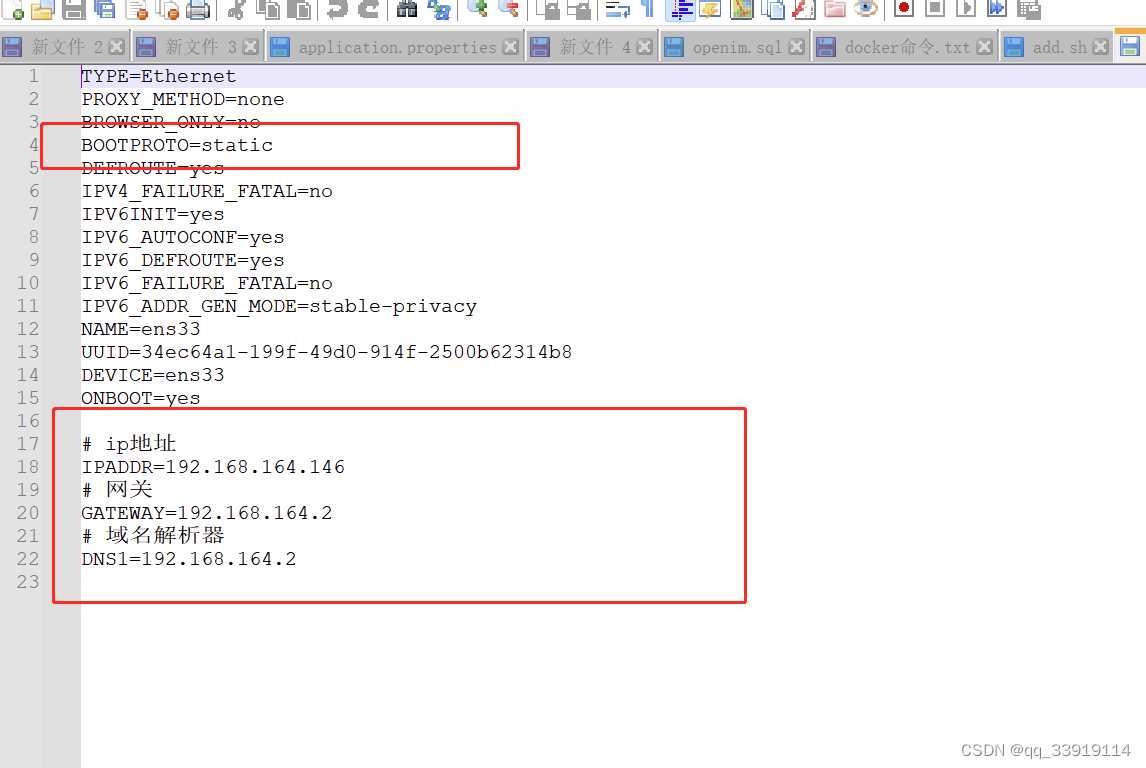
VMware 修改ip地址 虚拟机静态ip设置 centos动态ip修改为静态ip地址 centos静态ip地址 vmware修改ip地址
虚拟机的centos服务器经常变换ip,测试起来有些麻烦,故将动态ip修改为静态ip 1. 查看vmware 虚拟机网络配置: 点击编辑,打开虚拟网络配置 2. 选中nat模式,点击nat设置,最终获取网关ip: 192.168.164.2 3. 进…...

Deepin添加Ubuntu源
升级Deepin V23后,无法安装Zeal了,后面发现可以通过ubuntu源来安装。参考了以下两个文档。 添加Ubuntu源1 添加Ubuntu源2 1.添加ubuntu.list sudo vim /etc/apt/sources.list.d/ubuntu.list 2.添加中科大Ubuntu源 deb http://mirrors.ustc.edu.cn/…...

Mysql的多表查询和索引
MySQL 多表查询 当两个表查询时,从第一张表中取出一行和第二张表的每一行进行组合 返回结果含有两张表的所有列,一共返回的记录数第一张表行数*第二张表的行数(笛卡尔积) -- ?显示雇员名,雇员工资及所在部门的名字 【笛卡尔集…...

Java设计模式之建造者模式
建造者模式,又称生成器模式:将一个复杂的构建与其表示相分离,使得同样的构建过程可以创建不同的表示。 三个角色:建造者、具体的建造者、监工、使用者 建造者角色:定义生成实例所需要的所有方法; 具体的建…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
