NOIOLPJ2022B. 数学游戏 分析
数学游戏
题目描述
Kri 喜欢玩数字游戏。
一天,他在草稿纸上写下了 ttt 对正整数 (x,y)(x,y)(x,y),并对于每一对正整数计算出了 z=x×y×gcd(x,y)z = x \times y \times \gcd(x,y)z=x×y×gcd(x,y)。
可是调皮的 Zay 找到了 Kri 的草稿纸,并把每一组的 yyy 都擦除了,还可能改动了一些 zzz。
现在 Kri 想请你帮忙还原每一组的 yyy,具体地,对于每一组中的 xxx 和 zzz ,你需要输出最小的正整数 yyy,使得 z=x×y×gcd(x,y)z=x \times y \times \gcd(x,y)z=x×y×gcd(x,y)。如果这样的 yyy 不存在,也就是 Zay 一定改动了 zzz,那么请输出 −1-1−1。
注: gcd(x,y)\gcd(x,y)gcd(x,y) 表示 xxx 和 yyy 的最大公约数,也就是最大的正整数 ddd,满足 ddd 既是 xxx 的约数,又是 yyy 的约数。
输入格式
第一行一个整数 ttt,表示有 ttt 对正整数 xxx 和 zzz。
接下来 ttt 行,每行两个正整数 xxx 和 zzz,含义见题目描述。
输出格式
对于每对数字输出一行,如果不存在满足条件的正整数 yyy,请输出 −1-1−1,否则输出满足条件的最小正整数 yyy。
样例 1 解释
x×y×gcd(x,y)=10×12×gcd(10,12)=240x \times y \times \gcd(x,y) = 10 \times 12 \times \gcd(10,12) = 240x×y×gcd(x,y)=10×12×gcd(10,12)=240。
附加样例
见样例目录下的 math3.in 和 math3.out ,以及 math4.in 和 math4.out。
数据范围
对于 20%20\%20% 的数据,t,x,z≤103t,x,z \le 10^3t,x,z≤103。
对于 40%40\%40% 的数据,t≤103,x≤106,z≤109t \le 10^3,x \le 10^6,z \le 10^9t≤103,x≤106,z≤109。
对于另 30%30\%30% 的数据,t≤104t \le 10^4t≤104。
对于另 20%20\%20% 的数据,x≤106x \le 10^6x≤106。
对于 100%100\%100% 的数据,1≤t≤5×105,1≤x≤109,1≤z<2631 \le t \le 5 \times 10^5,1 \le x \le 10^9,1 \le z < 2^{63}1≤t≤5×105,1≤x≤109,1≤z<263。
题意简述
-
给定正整数 x,zx,zx,z,求满足 z=x×y×gcd(x,y)z=x\times y\times\gcd(x,y)z=x×y×gcd(x,y) 的最小正整数 yyy,若不存在,输出 −1-1−1。
-
每个测试点有 ttt 次询问。
-
1≤t≤5×1051\leq t\leq 5\times 10^51≤t≤5×105,1≤x≤1091\leq x\leq 10^91≤x≤109,1≤z≤2631\leq z\leq 2^{63}1≤z≤263
题目分析
方法一
设 x,y,zx,y,zx,y,z 中分别含有 x1,y1,z1x_1,y_1,z_1x1,y1,z1 个素因子 222,则 gcd(x,y)\gcd(x,y)gcd(x,y) 中含有 min(x1,y1)\min(x_1,y_1)min(x1,y1) 个素因子 222。
根据条件 z=x×y×gcd(x,y)z=x\times y\times\gcd(x,y)z=x×y×gcd(x,y) 得 z1=x1+y1+min(x1,y1)z_1=x_1+y_1+\min(x_1,y_1)z1=x1+y1+min(x1,y1),接着根据 x1x_1x1 和 y1y_1y1 的大小关系进行分类讨论:
-
x1>y1x_1>y_1x1>y1
此时 z1=x1+2y1z_1=x_1+2y_1z1=x1+2y1,且 x1>y1⇔3x1>z1x_1>y_1\Leftrightarrow 3x_1>z_1x1>y1⇔3x1>z1。注意 z1−x1z_1-x_1z1−x1 必须为偶数,否则 y1y_1y1 会出现小数的情况。 -
x1≤y1x_1\leq y_1x1≤y1
此时 z1=2x1+y1z_1=2x_1+y_1z1=2x1+y1,且 x1≤y1⇔3x1≤z1x_1\leq y_1\Leftrightarrow 3x_1\leq z_1x1≤y1⇔3x1≤z1。
综上,y1={z1−x12=z1−x12−z12,3x1>z1z1−2x1=z1−x12−3x12,3x1≤z1=z1−x12−min(3x1,z1)2y_1=\begin{cases} \dfrac{z_1-x_1}2=z_1-\dfrac{x_1}2-\dfrac{z_1}2,&3x_1>z_1\\ z_1-2x_1=z_1-\dfrac{x_1}2-\dfrac{3x_1}2,&3x_1\leq z_1 \end{cases}=z_1-\dfrac{x_1}2-\dfrac{\min(3x_1,z_1)}2y1=⎩ ⎨ ⎧2z1−x1=z1−2x1−2z1,z1−2x1=z1−2x1−23x1,3x1>z13x1≤z1=z1−2x1−2min(3x1,z1)。
同理,对于其他素因子,也满足上文所述。
再将这个等式转化成 x,y,zx,y,zx,y,z 的形式:
y=zx÷gcd(x3,z)=zx÷gcd(zx,x2)y=\dfrac z{\sqrt{x}}\div\sqrt{\gcd(x^3,z)}=\dfrac zx\div\sqrt{\gcd\left(\dfrac zx,x^2\right)} y=xz÷gcd(x3,z)=xz÷gcd(xz,x2)
方法二
令 g=gcd(x,y)g=\gcd(x,y)g=gcd(x,y),得
z=xyg⇒zx=yg⇒zx=yg×g2z=xyg \Rightarrow\dfrac zx=yg \Rightarrow\dfrac zx=\dfrac yg\times g^2z=xyg⇒xz=yg⇒xz=gy×g2
根据最大公约数性质,我们有 gcd(xg,yg)=1\gcd\left(\dfrac xg,\dfrac yg\right)=1gcd(gx,gy)=1,可得
gcd(zx,x2)=gcd[yg×g2,(xg)2×g2]=g2⇒g=gcd(zx,x2)⇒y=zx÷gcd(zx,x2)\begin{aligned} &\gcd\left(\dfrac zx,x^2\right)=\gcd\left[\dfrac yg\times g^2,\left(\dfrac xg\right)^2\times g^2\right]=g^2\\ \Rightarrow&g=\sqrt{\gcd\left(\dfrac zx,x^2\right)} \Rightarrow y=\dfrac zx\div\sqrt{\gcd\left(\dfrac zx,x^2\right)}\end{aligned}⇒gcd(xz,x2)=gcd[gy×g2,(gx)2×g2]=g2g=gcd(xz,x2)⇒y=xz÷gcd(xz,x2)
根据上述两种方法,均可证明 y=zx÷gcd(zx,x2)y=\dfrac zx\div\sqrt{\gcd\left(\dfrac zx,x^2\right)}y=xz÷gcd(xz,x2),故直接计算此式即可。
时间复杂度 Θ(tlogx2)\Theta(t\log x^2)Θ(tlogx2)。(注意计算 gcd\gcdgcd 的时间复杂度)
相关文章:

NOIOLPJ2022B. 数学游戏 分析
数学游戏 题目描述 Kri 喜欢玩数字游戏。 一天,他在草稿纸上写下了 ttt 对正整数 (x,y)(x,y)(x,y),并对于每一对正整数计算出了 zxygcd(x,y)z x \times y \times \gcd(x,y)zxygcd(x,y)。 可是调皮的 Zay 找到了 Kri 的草稿纸,并把每一组的…...
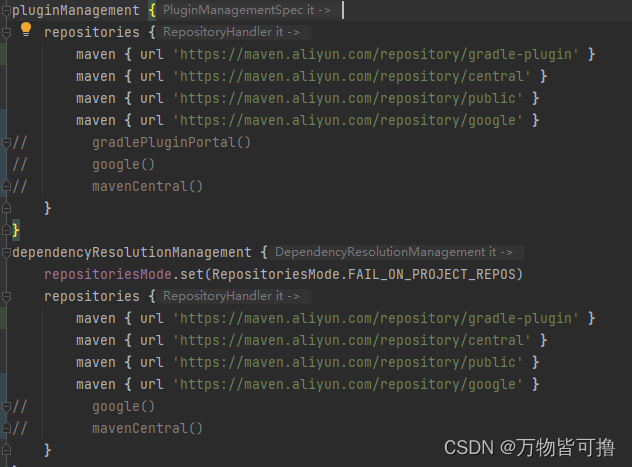
android studio gradle build running慢 卡住不动 失败 原因与解决方式
快速导航 分析原因解决办法 分析原因 主要原因是 gradle 构建时无法从网络获取需要的包或库。 解决办法 将国外库替换为阿里云镜像库。 例如 google 对应的库是 maven { url ‘https://maven.aliyun.com/repository/google’ }...

如何保障Facebook账号登录稳定
当谈到保障Facebook账号的稳定性时,我们不得不提到那些令人头疼的情况——Facebook账号被封。尽管我们已经踏入数字化的未来,但是被封号似乎是一个时常困扰着社交媒体用户的问题。那么,让我们来看看一些常见的Facebook账号被封的原因…...

当前目录下的excel文件的两列内容的相似度比较
# -- coding: utf-8 --** from sklearn.feature_extraction.text import CountVectorizer from sklearn.metrics.pairwise import cosine_similarity import numpy as np import pandas as pd import os # 获取当前目录 current_dir os.getcwd() # 获取当前目录下所有xlsx文件…...

Cookie for Mac:隐私保护工具保护您的在线隐私
随着互联网的发展,我们每天都会浏览各种网站,享受在线购物、社交娱乐和学习资料等各种便利。然而,您是否曾经遇到过需要频繁输入用户名和密码的情况?或者不方便访问您常用的网站?如果是这样,那么Cookie for…...

Huggingface训练Transformer
在之前的博客中,我采用SFT(监督优化训练)的方法训练一个GPT2的模型,使得这个模型可以根据提示语进行回答。具体可见博客召唤神龙打造自己的ChatGPT_gzroy的博客-CSDN博客 Huggingface提供了一个TRL的扩展库,可以对tra…...

IA-YOLO项目中DIP模块的初级解读
IA-YOLO项目源自论文Image-Adaptive YOLO for Object Detection in Adverse Weather Conditions,其提出端到端方式联合学习CNN-PP和YOLOv3,这确保了CNN-PP可以学习适当的DIP,以弱监督的方式增强图像检测。IA-YOLO方法可以自适应地处理正常和不…...
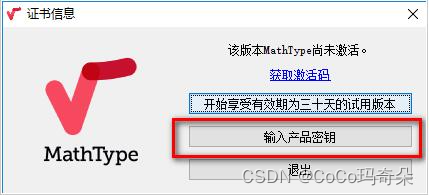
MathType7.4mac最新版本数学公式编辑器安装教程
MathType7.4中文版是一款功能强大且易于使用的公式编辑器。该软件可与word软件配合使用,有效提高了教学人员的工作效率,避免了一些数学符号和公式无法在word中输入的麻烦。新版MathType7.4启用了全新的LOGO,带来了更多对数学符号和公式的支持…...
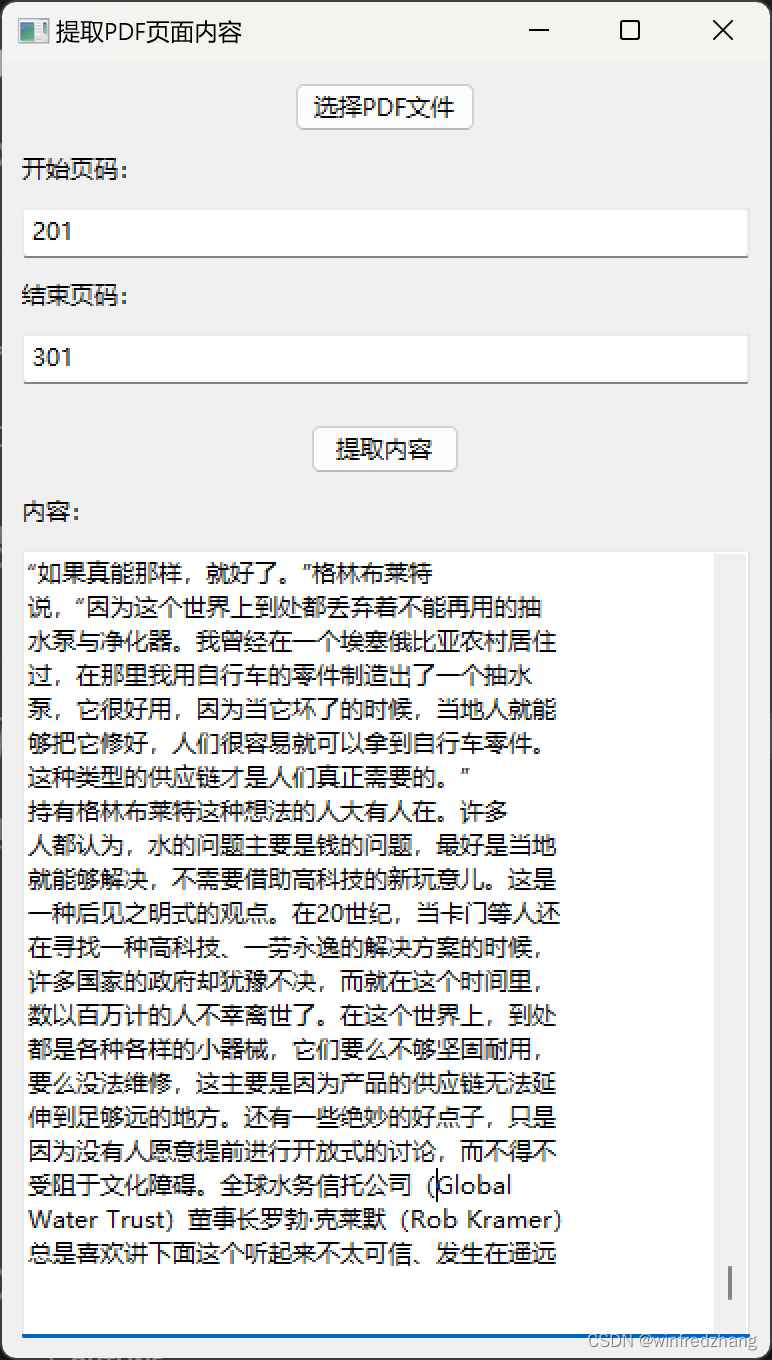
为Claude的分析内容做准备:提取PDF页面内容的简易应用程序
由于Claude虽然可以分析整个文件,但是对文件的大小以及字数是有限制的,为了将pdf文件分批传入Claude人工智能分析和总结文章内容,才有了这篇博客: 在本篇博客中,我们将介绍一个基于 wxPython 和 PyMuPDF 库编写的简易的…...
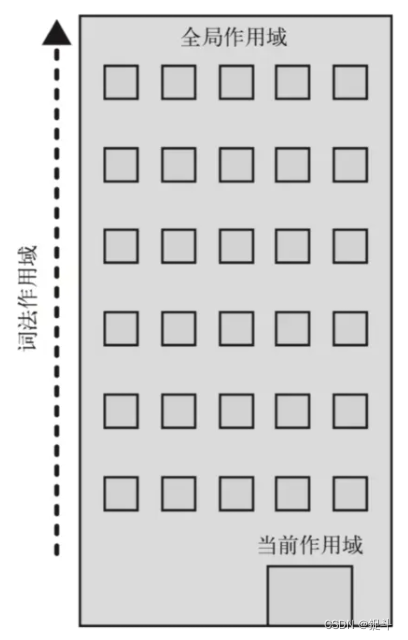
js中作用域的理解?
1.作用域 作用域,即变量(变量作用域又称上下文)和函数生效(能被访问)的区域或集合 换句话说,作用域决定了代码区块中变量和其他资源的可见性 举个例子 function myFunction() {let inVariable "函数内部变量"; } myFunction();//要先执行这…...
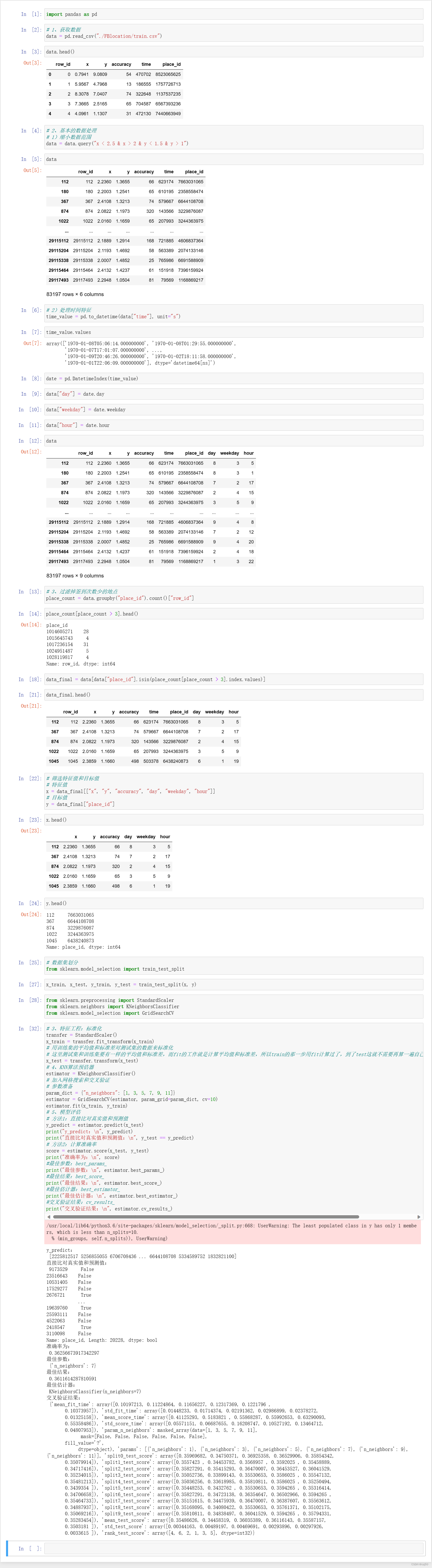
机器学习基础之《分类算法(4)—案例:预测facebook签到位置》
一、背景 1、说明 2、数据集 row_id:签到行为的编码 x y:坐标系,人所在的位置 accuracy:定位的准确率 time:时间戳 place_id:预测用户将要签到的位置 3、数据集下载 https://www.kaggle.com/navoshta/gr…...

【Java】反射 之 调用方法
调用方法 我们已经能通过Class实例获取所有Field对象,同样的,可以通过Class实例获取所有Method信息。Class类提供了以下几个方法来获取Method: Method getMethod(name, Class...):获取某个public的Method(包括父类&a…...

Java——单例设计模式
什么是设计模式? 设计模式是在大量的实践中总结和理论化之后优选的代码结构、编程风格、以及解决问题的思考方式。设计模式免去我们自己再思考和摸索。就像是经典的棋谱,不同的棋局,我们用不同的棋谱、“套路”。 经典的设计模式共有23种。…...

Java实现excel表数据的批量存储(结合easyexcel插件)
场景:加哥最近在做项目时,苦于系统自身并未提供数据批量导入的功能还不能自行添加上该功能,且自身不想手动一条一条将数据录入系统。随后,自己使用JDBC连接数据库、使用EasyExcel插件读取表格并将数据按照业务逻辑批量插入数据库完…...
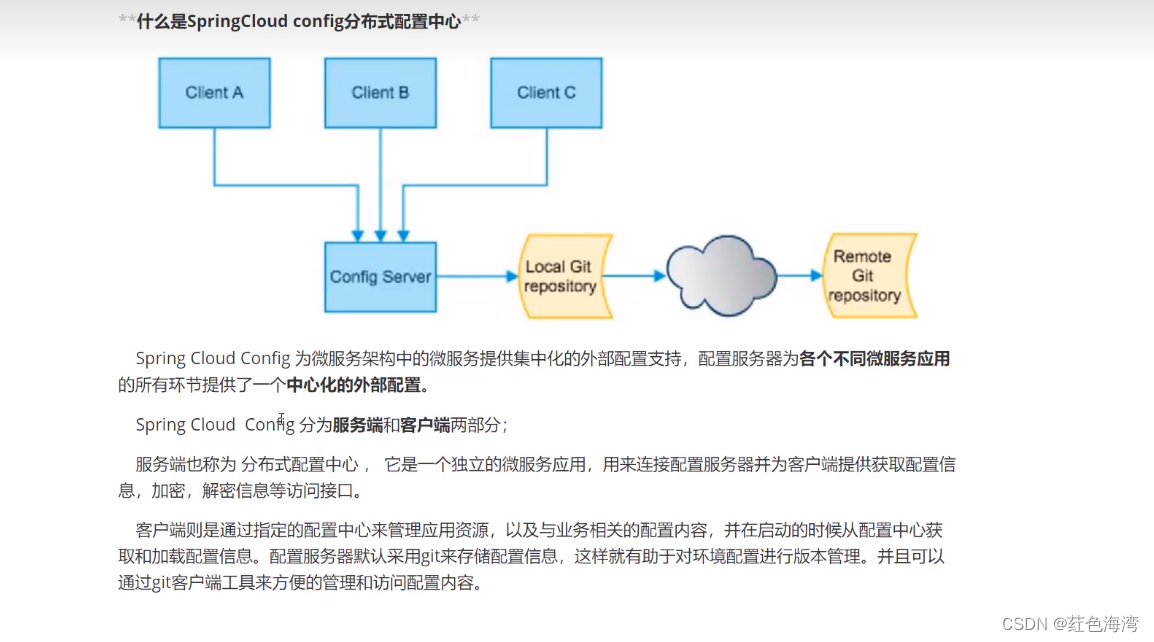
Config:客户端连接服务器访问远程
springcloud-config: springcloud-config push pom <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocatio…...

【KMP算法-代码随想录】
目录 1.什么是KMP2.什么是next数组3.什么是前缀表(1)前后缀含义(2)最长公共前后缀(3)前缀表的必要性 4.计算前缀表5.前缀表与next数组(1)使用next数组来匹配 6.构造next数组…...
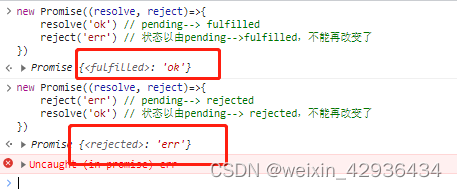
【手写promise——基本功能、链式调用、promise.all、promise.race】
文章目录 前言一、前置知识二、实现基本功能二、实现链式调用三、实现Promise.all四、实现Promise.race总结 前言 关于动机,无论是在工作还是面试中,都会遇到Promise的相关使用和原理,手写Promise也有助于学习设计模式以及代码设计。 本文主…...
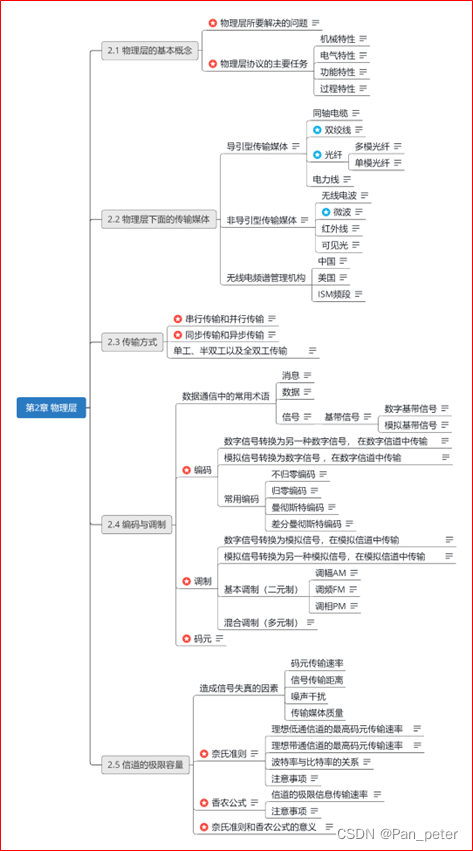
计算机网络-笔记-第二章-物理层
目录 二、第二章——物理层 1、物理层的基本概念 2、物理层下面的传输媒体 (1)光纤、同轴电缆、双绞线、电力线【导引型】 (2)无线电波、微波、红外线、可见光【非导引型】 (3)无线电【频谱的使用】 …...

前端开发中的单伪标签清除和双伪标签清除
引言 在前端开发中,我们经常会遇到一些样式上的问题,其中之一就是伪元素造成的布局问题。为了解决这个问题,我们可以使用伪标签清除技术。本篇博客将介绍单伪标签清除和双伪标签清除的概念、用法和示例代码,并详细解释它们的原理…...

云计算中的数据安全与隐私保护策略
文章目录 1. 云计算中的数据安全挑战1.1 数据泄露和数据风险1.2 多租户环境下的隔离问题 2. 隐私保护策略2.1 数据加密2.2 访问控制和身份验证 3. 应对方法与技术3.1 零知识证明(Zero-Knowledge Proofs)3.2 同态加密(Homomorphic Encryption&…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...
