五分钟了解最短路径寻路算法:Dijkstra 迪杰斯特拉
最短路径查找算法
寻路算法在生活中应用十分常见。本文实现的是关于图的最短路径查找算法。
该算法比较常见于游戏和室内地图导航。
实现
例子:几个节点之间,相连接的线段有固定长度,该长度决就是通过代价。查找到花费最少的路径。该图结构为
思路:
可以看到 A>B>D与A>C>D 的代价都相同,边相加都等于10. 而A>C>B的路线代价扽与9,是最短路径。
- 将每个节点的子节点包括路径都保存成散列表。
- 递归检查每个相关节点,看是否能到达终点,并记录下代价、路线、并保存好与上次成功到达终点的路径相比,代价较小的路径。
- 不断更新直到循环每个节点。
- 最后输出的结果就是想要的最短路径
复杂度:最坏情况应该就是O((n-1)2) 了吧
不参考加权,求任意两点间的所有路径
//csharp版代码using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Collections;namespace ConsoleApp1test
{class Program{ //创建图数据static Hashtable myGraph = new Hashtable();static void Main(string[] args) {//A节点及其信息与关系myGraph["A"] = new Hashtable();(myGraph["A"] as Hashtable)["B"] = 5;(myGraph["A"] as Hashtable)["C"] = 2;(myGraph["A"] as Hashtable)["F"] = 2;//B节点myGraph["B"] = new Hashtable();(myGraph["B"] as Hashtable)["D"] = 5;(myGraph["B"] as Hashtable)["F"] = 5;//CmyGraph["C"] = new Hashtable();(myGraph["C"] as Hashtable)["B"] = 2;(myGraph["C"] as Hashtable)["D"] = 8;//DmyGraph["D"] = new Hashtable();//fmyGraph["F"] = new Hashtable();//递归监测GetPath(myGraph["A"] as Hashtable, "A", "D");Console.ReadKey();}//创建用于存储代价的变量static int cost = 0;//创建用于记录路径的数据表static Hashtable rote = new Hashtable();static List<string> rotearray = new List<string>();public static void GetPath(Hashtable targetNode, string startPoint, string endPoint){//记录当前节点rotearray.Add(startPoint);Console.WriteLine("当前节点:"+ startPoint);string st = "";foreach (string name in rotearray){st += name + ">";}Console.WriteLine("当前结构:"+st);//当前节点是否是根节点if (startPoint == endPoint){//已经到达终点 //输出当前分支的每个节点string s = "";foreach (string name in rotearray){s += name + ">";}Console.WriteLine("到达终点,路径:"+s);Console.WriteLine("=================");} else {//未到达指定节点 遍历每个节点下相关联的子节点foreach (string connected_node_name in targetNode.Keys)//在第一次输入时,不应该遍历所有的值{GetPath(myGraph[connected_node_name] as Hashtable, connected_node_name, endPoint);}}//删除当前节点回 到上层if (rotearray.Count > 0)rotearray.RemoveAt(rotearray.Count - 1);}}
}结果:
当前节点:A
当前结构:A>
当前节点:C
当前结构:A>C>
当前节点:D
当前结构:A>C>D>
到达终点,路径:A>C>D>
=================
当前节点:B
当前结构:A>C>B>
当前节点:F
当前结构:A>C>B>F>
当前节点:D
当前结构:A>C>B>D>
到达终点,路径:A>C>B>D>
=================
当前节点:F
当前结构:A>F>
当前节点:B
当前结构:A>B>
当前节点:F
当前结构:A>B>F>
当前节点:D
当前结构:A>B>D>
到达终点,路径:A>B>D>
=================求指定两点间代价最小(最短)路径
此段代码,用于求出加权图最短路径,加入了防循环,可以在有向图、无向图中使用
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Collections;namespace ConsoleApp1test
{class Program{ //创建图数据static Hashtable myGraph = new Hashtable();static void Main(string[] args) {//A节点及其信息与关系myGraph["A"] = new Hashtable();(myGraph["A"] as Hashtable)["B"] = 5;(myGraph["A"] as Hashtable)["C"] = 2;(myGraph["A"] as Hashtable)["F"] = 2;//B节点myGraph["B"] = new Hashtable();(myGraph["B"] as Hashtable)["D"] = 5;(myGraph["B"] as Hashtable)["F"] = 5;//CmyGraph["C"] = new Hashtable();(myGraph["C"] as Hashtable)["B"] = 2;(myGraph["C"] as Hashtable)["D"] = 8;//DmyGraph["D"] = new Hashtable();//fmyGraph["F"] = new Hashtable();(myGraph["F"] as Hashtable)["B"] = 2;//递归监测GetPath(myGraph["A"] as Hashtable, "A", "D");Console.WriteLine("最短路径:" + shortestPath + " 代价:" + shortestCost + "米");Console.ReadKey();}//创建用于存储代价\记录路径的数据表static List<string> pathList = new List<string>();static List<int> pathCostList = new List<int>();static int shortestCost = 100000;static string shortestPath = "";public static void GetPath(Hashtable targetNode, string startPoint, string endPoint){//记录当前节点pathList.Add(startPoint);Console.WriteLine("当前节点:"+ startPoint);string allPath = "";for(int i=0; i < pathList.Count; i++){allPath += pathList[i];allPath += (i == (pathList.Count - 1)) ? "" : ">";}Console.WriteLine("当前结构:" + allPath);//当前节点是否是根节点if (startPoint == endPoint){//已经到达终点 //输出当前分支的每个节点Console.WriteLine("到达终点,路径:"+ allPath);//计算所有的权值int pathCost_total = 0;foreach (int pathCost in pathCostList){pathCost_total += pathCost;}Console.WriteLine("代价:" + pathCost_total.ToString() + "米");//更新最短路径信息if (pathCost_total < shortestCost) {shortestCost = pathCost_total;shortestPath = allPath;}Console.WriteLine("==========害羞而淫荡的分割线==========");} else {//未到达指定节点 遍历每个节点下相关联的子节点foreach (string connected_node_name in targetNode.Keys){//如果,路径中已存在节点,就不走了。 避免循环。if (!pathList.Contains(connected_node_name)) {//记录路径权值pathCostList.Add((int)targetNode[connected_node_name]);GetPath(myGraph[connected_node_name] as Hashtable, connected_node_name, endPoint);//记录路径权值if (pathCostList.Count > 0)pathCostList.RemoveAt(pathCostList.Count - 1);}}}//删除当前节点回 到上层if (pathList.Count > 0)pathList.RemoveAt(pathList.Count - 1);}}
}结果:
当前节点:A
当前结构:A
当前节点:C
当前结构:A>C
当前节点:D
当前结构:A>C>D
到达终点,路径:A>C>D
代价:10米
==========害羞而淫荡的分割线==========
当前节点:B
当前结构:A>C>B
当前节点:F
当前结构:A>C>B>F
当前节点:D
当前结构:A>C>B>D
到达终点,路径:A>C>B>D
代价:9米
==========害羞而淫荡的分割线==========
当前节点:F
当前结构:A>F
当前节点:B
当前结构:A>F>B
当前节点:D
当前结构:A>F>B>D
到达终点,路径:A>F>B>D
代价:9米
==========害羞而淫荡的分割线==========
当前节点:B
当前结构:A>B
当前节点:F
当前结构:A>B>F
当前节点:D
当前结构:A>B>D
到达终点,路径:A>B>D
代价:10米
==========害羞而淫荡的分割线==========
最短路径:A>C>B>D 代价:9米有权图,理论上来说把权化为等量节点,也可以使用最短节点算法求最短路径。
相关文章:

五分钟了解最短路径寻路算法:Dijkstra 迪杰斯特拉
最短路径查找算法 寻路算法在生活中应用十分常见。本文实现的是关于图的最短路径查找算法。 该算法比较常见于游戏和室内地图导航。 实现 例子:几个节点之间,相连接的线段有固定长度,该长度决就是通过代价。查找到花费最少的路径。该图结构…...
【ARM】Day8 中断
1. 思维导图 2. 实验要求: 实现KEY1/LEY2/KE3三个按键,中断触发打印一句话,并且灯的状态取反 key1 ----> LED3灯状态取反 key2 ----> LED2灯状态取反 key3 ----> LED1灯状态取反 key3.h #ifndef __KEY3_H__ #define __KEY3_H__#in…...

大数据Flink(六十八):SQL Table 的基本概念及常用 API
文章目录 SQL & Table 的基本概念及常用 API 一、一个 Table API\SQL任务的代码结构...

算法练习- 其他算法练习6
文章目录 数字序列比大小最佳植树距离文艺汇演计算误码率二维伞的雨滴效应阿里巴巴找黄金宝箱4 数字序列比大小 A、B两人一人一个整数数组,长度相等,元素随即;两人随便拿出一个元素(弹出),比较大小&#x…...

ModaHub魔搭社区:WinPlan经营大脑管理中心
角色权限 展示设置的角色,及对应的成员及权限点。角色、成员、权限点可自由配置;管理员的角色不可删除、权限点默认全部不可更改。 WinPlan决策系统 算力 阿里云 腾讯云 AWS亚马逊 框架 业务数据基座 WinPlan垂直大模型 模型 分...
滑动窗口系列4-Leetcode322题零钱兑换-限制张数-暴力递归到动态规划再到滑动窗口
这个题目是Leecode322的变种,322原题如下: 我们这里的变化是把硬币变成可以重复的,并且只有coins数组中给出的这么多的金币,也就是说有数量限制: package dataStructure.leecode.practice;import java.util.Arrays; i…...
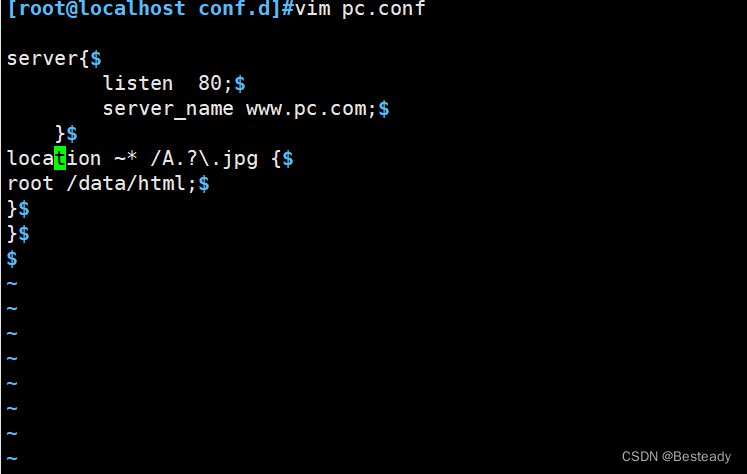
Nginx全局配置
一、修改启动进程数 worker_processes 1; #允许的启动工作进程数数量,和你真实的cpu数量有关 1 worker_processes auto; #如果设置为auto 就是你真实的cpu数量 ps axo pid,cmd,psr,ni|grep nginx #可以看到 nginx的 worker数量 二、日制分割 [rootyuji ~]#…...

VUE笔记(四)vue的组件
一、组件的介绍 1、组件的作用 整个项目都是由组件组成 可以让代码复用:相似结构代码可以做成一个组件,直接进行调用就可以使用,提高代码复用性 可以让代码具有可维护性(只要改一处,整个引用的部分全部都变…...

菜鸟教程《Python 3 教程》笔记
菜鸟教程《Python 3 教程》笔记 0 写在前面1 基本数据类型1.1 Number(数字)1.2 String(字符串)1.3 bool(布尔类型)1.4 List(列表)1.5 Tuple(元组)1.6 Set&…...

JAVA学习-愚见
JAVA学习-愚见 分享一下Java的学习路线,仅供参考【本人亲测,真实有效】 1、尽可能推荐较新的课程 2、大部分视频在B站上直接搜关键词就行【自学,B大的学生】 文章目录 JAVA学习-愚见前期准备Java基础课程练手项目 数据库JavaWeb前端基础 Vue…...

Watch数据监听详解
一、Vue2写法 1、watch使用的几种方法 1、通过 watch 监听 data 数据的变化,数据发生变化时,就会打印当前的值 watch: {data(val, value) {console.log(val)console.log(value)}} 2、通过 watch 监听 list 数据的变化,数据发生变化时&…...
UML建模以及几种类图的理解
文章目录 前言1.用例与用例图1.1 参与者1.2 用例之间的关系1.3 用例图1.4 用例的描述 2.交互图2.1 顺序图2.2 协作图 3.类图和对象图3.1 关联关系3.2 聚合和组合3.3 泛化关系3.4 依赖关系 4.状态图与活动图4.1 状态图4.2 活动图 5.构件图 前言 UML通过图形化的表示机制从多个侧…...
opencv进阶18-基于opencv 决策树导论
1. 什么是决策树? 决策树是最早的机器学习算法之一,起源于对人类某些决策过程 的模仿,属于监督学习算法。 决策树的优点是易于理解,有些决策树既可以做分类,也可以做回归。在排名前十的数据挖掘算法中有两种是决策树[1…...

13.4 目标检测锚框标注 非极大值抑制
锚框的形状计算公式 假设原图的高为H,宽为W 锚框形状详细公式推导 以每个像素为中心生成不同形状的锚框 # s是缩放比,ratio是宽高比 def multibox_prior(data, sizes, ratios):"""生成以每个像素为中心具有不同形状的锚框"""in_he…...
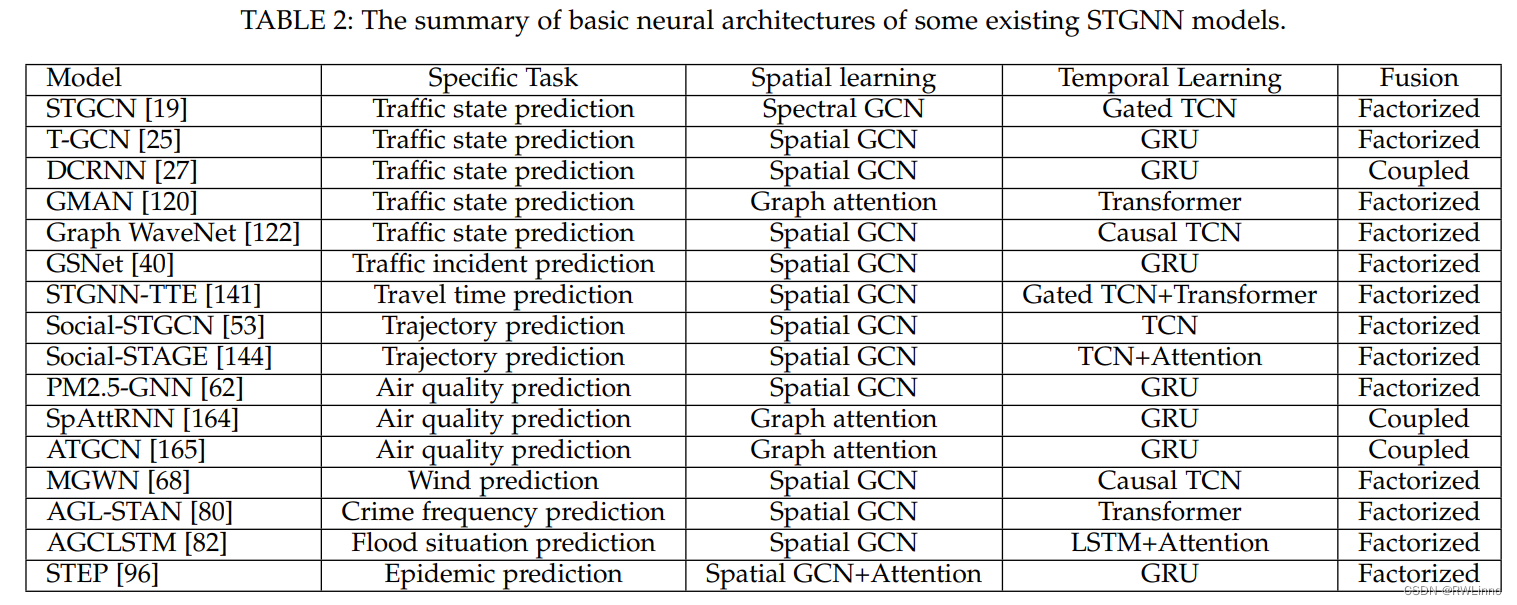
【论文笔记】最近看的时空数据挖掘综述整理8.27
Deep Learning for Spatio-Temporal Data Mining: A Survey 被引用次数:392 [Submitted on 11 Jun 2019 (v1), last revised 24 Jun 2019 (this version, v2)] 主要内容: 该论文是一篇关于深度学习在时空数据挖掘中的应用的综述。论文首先介绍了时空数…...

【大模型】基于 LlaMA2 的高 star 的 GitHub 开源项目汇总
【大模型】基于 LlaMA2 的高 star 的 GitHub 开源项目汇总 Llama2 简介开源项目汇总NO1. FlagAlpha/Llama2-ChineseNO2. hiyouga/LLaMA-Efficient-TuningNO3. yangjianxin1/FireflyNO4. LinkSoul-AI/Chinese-Llama-2-7bNO5. wenge-research/YaYiNO6. michael-wzhu/Chinese-LlaM…...
解决elementUI打包上线后icon图标偶尔乱码的问题
解决vue-elementUI打包后icon图标偶尔乱码的问题 一、背景二、现象三、原因四、处理方法方式1:使用css-unicode-loader方式2:升高 sass版本到1.39.0方式3:替换element-ui的样式文件方式4:更换打包压缩方式知识扩展:方式…...

yolov3加上迁移学习和适度的数据增强形成的网络应用在输电线异物检测
Neural Detection of Foreign Objects for Transmission Lines in Power Systems Abstract. 输电线路为电能从一个地方输送到另一个地方提供了一条路径,确保输电线路的正常运行是向城市和企业供电的先决条件。主要威胁来自外来物,可能导致电力传输中断。…...

香橙派OrangePi zero H2+ 驱动移远EC200A
1 系统内核: Linux orangepizero 5.4.65-sunxi #2.2.2 SMP Tue Aug 15 17:45:28 CST 2023 armv7l armv7l armv7l GNU/Linux 1.1 下载内核头安装 下载:orangepi800 内核头rk3399链接https://download.csdn.net/download/weixin_37613240/87635781 1.1.1…...
)
写一个java中如何用JSch来连接sftp的类并做测试?(亲测)
当使用JSch连接SFTP服务器的类,并进行测试时,可以按照以下步骤操作: 添加JSch库的依赖项。在你的项目中添加JSch库的Maven依赖项(如前面所述)或下载JAR文件并将其包含在项目中。 <dependency> <groupId&…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
