LeetCode 周赛上分之旅 #42 当 LeetCode 考树上倍增,出题的趋势在变化吗
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。
学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度也更复杂。在这个专栏里,小彭与你分享每场 LeetCode 周赛的解题报告,一起体会上分之旅。
本文是 LeetCode 上分之旅系列的第 42 篇文章,往期回顾请移步到文章末尾~
周赛 360
T1. 距离原点最远的点(Easy)
- 标签:模拟
T2. 找出美丽数组的最小和(Medium)
- 标签:散列表、贪心、数学
T3. 使子序列的和等于目标的最少操作次数(Hard)
- 标签:位运算、散列表、排序
T4. 在传球游戏中最大化函数值(Hard)
- 标签:树、倍增、动态规划、内向基环树
T1. 距离原点最远的点(Easy)
https://leetcode.cn/problems/furthest-point-from-origin/
题解(模拟)
根据题意 “_” 既可以作为 “L” 也可以作为 “R”。容易想到,为了使得终点距离原点更远,当所有 “_” 仅作为 “L” 或 “R” 对结果的贡献是最优的,此时问题的结果就取决于 “L” 和 “R” 的差绝对值。
class Solution {fun furthestDistanceFromOrigin(moves: String): Int {return moves.count{ it == '_' } + abs(moves.count{ it == 'L' } - moves.count{ it == 'R' })}
}
一次遍历:
class Solution {fun furthestDistanceFromOrigin(moves: String): Int {var cntL = 0var cntR = 0for (e in moves) {when (e) {'L' -> {cntL ++cntR --}'R' -> {cntL --cntR ++}else -> {cntL ++cntR ++}}}return max(abs(cntL), abs(cntR))}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 线性遍历;
- 空间复杂度: O ( 1 ) O(1) O(1) 仅使用常量级别空间。
T2. 找出美丽数组的最小和(Medium)
https://leetcode.cn/problems/find-the-minimum-possible-sum-of-a-beautiful-array/
这道题与上周周赛 359 T2 2829. k-avoiding 数组的最小总和 相比,除了数据范围之外是完全相同的,有点离谱。
题解一(散列表 + 贪心)
从 1 1 1 开始从小到大枚举,如果当前元素 c u r cur cur 与已选列表不冲突,则加入结果中。为了验证是否冲突,我们使用散列表在 O ( 1 ) O(1) O(1) 时间复杂度判断。
class Solution {fun minimumPossibleSum(n: Int, k: Int): Long {val set = HashSet<Int>()var sum = 0Lvar cur = 1repeat(n) {while (!set.isEmpty() && set.contains(k - cur)) cur++sum += curset.add(cur)cur++}return sum}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 线性遍历;
- 空间复杂度: O ( n ) O(n) O(n) 散列表空间。
题解二(数学)
这道题还可以继续挖掘数学规律,我们发现当我们从 1 1 1 开始从小到大枚举时,每选择一个数的同时必然会使得另一个数 k − x k - x k−x 不可选。例如:
- 选择 1 1 1,则 k − 1 k - 1 k−1 不可选;
- 选择 2 2 2,则 k − 2 k - 2 k−2 不可选;
- …
- 选择 k / 2 k / 2 k/2,则 k − k / 2 k - k / 2 k−k/2 不可选。
可以发现,最终选择的元素被分为两部分:
- 小于 k k k 的部分:选择所有和为 k k k 的配对中的较小值,即 1 、 2 、 3 … k / 2 1、2、3 … k / 2 1、2、3…k/2;
- 大于等于 k k k 的部分:与其他任意正整数相加都不会等于 k k k,因此大于等于 k k k 的数必然可以选择,即 k 、 k + 1 、 k + 2 、 … 、 k + n − m − 1 k、k + 1、k + 2、…、k + n - m - 1 k、k+1、k+2、…、k+n−m−1 共 n - m 个数。
我们令 m = m i n ( k / 2 , n ) m = min(k / 2, n) m=min(k/2,n),使用求和公式可以 O ( 1 ) O(1) O(1) 求出两部分的总和:
- 小于 k 的部分: m ( m + 1 ) / 2 m(m + 1)/ 2 m(m+1)/2
- 大于等于 k 的部分: ( n − m ) ∗ ( 2 ∗ k + n − m − 1 ) / 2 (n - m) * (2*k + n - m - 1) / 2 (n−m)∗(2∗k+n−m−1)/2
class Solution {fun minimumPossibleSum(n: Int, k: Int): Long {val m = 1L * Math.min(n, k / 2)return m * (m + 1) / 2 + (n - m) * (2 * k + n - m - 1) / 2}
}
复杂度分析:
- 时间复杂度: O ( 1 ) O(1) O(1)
- 空间复杂度: O ( 1 ) O(1) O(1)
T3. 使子序列的和等于目标的最少操作次数(Hard)
https://leetcode.cn/problems/minimum-operations-to-form-subsequence-with-target-sum/
这道题的考点不复杂,难点在模拟问题挺考验编码功底的。
问题分析
- 关键信息: n u m s nums nums 数组中所有元素都是 2 2 2 的幂,元素顺序对结果没有影响;
- 问题是否有解: 考虑到所有数最终都能拆分成 1 1 1,那么只要 n u m s nums nums 数组的和大于等于 t a r g e t target target 就一定有解;
# 二进制位
nums: _ _ _ 1 _ _ _ _
target: _ _ _ _ _ 1 _ _
- 子问题: 问题是否有解的判断不仅适用于原问题,对于仅考虑二进制位最低位 [ 0 ] [0] [0] 到 [ k ] [k] [k] 的子问题亦是如此。
以示例 1 nums = [1,2,8], target = 7 与示例 2 nums = [1,32,1,2], target = 12 为例,我们将统计 n u m s nums nums 中不同 2 2 2 的幂的出现次数:
# 二进制位
nums: _ _ _ _ 1 _ 1 1
target: _ _ _ _ _ 1 1 1# 二进制位
nums: _ _ 1 _ _ _ 1 2 # 1 出现 2 次
target: _ _ _ _ 1 1 _ _
那么当我们从右向左枚举二进制位 k k k 时,如果「 n u m s nums nums 中小于等于 2 k 2^k 2k 的元素和」 ≥ ≥ ≥ 「 t a r g e t target target 中低于等于 k k k 位的值」,那么对于仅考虑 [ 0 , k ] [0, k] [0,k] 位上的子问题是有解的。否则,我们需要找到 n u m s nums nums 中最近大于 2 k 2^k 2k 的最近数组做拆分:
# 只考虑低 2 位,可以构造
nums: _ _ _ _ 1 _ | 1 1
target: _ _ _ _ _ 1 | 1 1# 只考虑低 3 位,无法构造,需要找到最近的 “1” 做拆分
nums: _ _ _ _ 1 | _ 1 1
target: _ _ _ _ _ | 1 1 1# 只考虑低 3 位,无法构造,需要找到最近的 “1” 做拆分
nums: _ _ 1 _ _ | _ 1 2
target: _ _ _ _ 1 | 1 _ _# 只考虑低 6 位,可以构造
nums: _ _ | 1 _ _ _ 1 2
target: _ _ | _ _ 1 1 _ _
组合以上技巧:
写法一(数组模拟)
思路参考灵神的题解。
- 首先,我们使用长为 32 32 32 的数组,计算出 n u m s nums nums 数组中每个 2 2 2 的幂的出现次数;
- 随后,我们从低位到高位枚举二进制位 i i i,在每轮迭代中将 n u m s nums nums 数组中的 2 i 2^i 2i 元素累加到 s u m sum sum 中,此举相当于在求「低 i i i 位的子问题」可以构造的最大值;
- 最后,我们比较 s u m sum sum 是否大于等于 t a r g e t target target(只考虑低 i i i 位),此举相当于在判断「低 i i i 位的子问题」是否可构造。如果不可构造,我们尝试寻找最近的 2 j 2^j 2j 做拆分;
- 另外,有一个优化点:当我们拆分将 2 j 2^j 2j 拆分到 2 i ( j > i ) 2^i (j > i) 2i(j>i) 时并不是直接丢弃 2 j 2^j 2j,而是会留下 2 j − 1 、 2 j − 2 … 2 i 2^{j-1}、2^{j-2}… 2^i 2j−1、2j−2…2i 等一系列数,可以直接跳到第 j j j 位继续枚举。
注意一个容易 WA 的地方,在开头特判的地方,由于元素和可能会溢出 I n t Int Int 上界,所以我们需要转换为在 L o n g Long Long 上的求和。
class Solution {fun minOperations(nums: List<Int>, target: Int): Int {if (nums.fold(0L) { it, acc -> it + acc } < target) return -1// if (nums.sum() < target) return -1 // 溢出// 计数val cnts = IntArray(32)for (num in nums) {var i = 0var x = numwhile (x > 1) {x = x shr 1i += 1}cnts[i]++}var ret = 0var i = 0var sum = 0Lwhile(sum < target) {// 累加低位的 numssum += (cnts[i]) shl i// println("i=$i, sum=$sum")// 低 i 位掩码val mask = (1 shl (i + 1)) - 1// 构造子问题if (sum < target and mask) {var j = i + 1while (cnts[j] == 0) { // 基于开头的特判,此处一定有解j++}// 拆分ret += j - ii = j} else {i += 1}}return ret}
}
复杂度分析:
- 时间复杂度: O ( n ⋅ U + U O(n·U + U O(n⋅U+U) 其中 n n n 为 n u m s nums nums 数组的长度, U U U 为整型大小 32 32 32;
- 空间复杂度: O ( U ) O(U) O(U) 数组空间。
写法二(散列表模拟)
在计数的部分,我们可以使用散列表模拟,复杂度相同。
class Solution {fun minOperations(nums: List<Int>, target: Int): Int {if (nums.fold(0L) { it, acc -> it + acc } < target) return -1// if (nums.sum() < target) return -1 // 溢出// 计数val cnts = HashMap<Int, Int>()for (num in nums) {cnts[num] = cnts.getOrDefault(num, 0) + 1}var ret = 0var i = 0var sum = 0Lwhile(sum < target) {// 累加低位的 numssum += (cnts[1 shl i] ?: 0) shl i// println("i=$i, sum=$sum")// 低 i 位掩码val mask = (1 shl (i + 1)) - 1// 构造子问题if (sum < target and mask) {var j = i + 1while (!cnts.containsKey(1 shl j)) { // 基于开头的特判,此处一定有解j++}// 拆分ret += j - ii = j} else {i += 1}}return ret}
}
复杂度分析:
- 时间复杂度: O ( n + U ) O(n + U) O(n+U) 其中 n n n 为 n u m s nums nums 数组的长度, U U U 为整型大小 32 32 32;
- 空间复杂度: O ( U ) O(U) O(U) 散列表空间。
写法三(逆向思维)
思路参考雪景式的题解,前两种写法是在从小到大枚举「选哪个」,我们也可以枚举「不选哪个」。
- 思考 1: 在原问题有解 ( s u m > t a r g e t ) (sum > target) (sum>target)的情况下,如果从 s u m sum sum 中剔除最大的元素 x x x 后,依然满足剩余的元素和 s u m ’ > t a r g e t sum’ > target sum’>target,那么直接将 x x x 去掉,这是因为一定存在比 x x x 操作次数更小的方案能够构造 t a r g e t target target(元素越大拆分次数越多)。
- 思考 2: 如果从 s u m sum sum 中剔除最大的元素 x x x 后不能构造,说明 x x x 是一定要选择或者拆分,此时考虑 x x x 对 t a r g e t target target 的影响:
- 如果 x > t a r g e t x > target x>target,那么 x x x 需要先拆分
- 如果 x ≤ t a r g e t x ≤ target x≤target,那么 x x x 可以被选择并抵消 t a r g e t target target
class Solution {fun minOperations(nums: MutableList<Int>, target: Int): Int {var sum = nums.fold(0L) { it, acc -> it + acc }if (sum < target) return -1// 排序nums.sortDescending()// 从大到小枚举var ret = 0var left = targetwhile (sum > left) {val x = nums.removeFirst()if (sum - x >= left){sum -= x} else if (x <= left) {sum -= xleft -= x} else {ret += 1nums.add(0, x / 2)nums.add(0, x / 2)}// println("ret=$ret, sum=$sum, left=$left, x=$x, nums=${nums.joinToString()}")}return ret}
}
复杂度分析:
- 时间复杂度: O ( n l g n + n + U ) O(nlgn + n + U) O(nlgn+n+U) 瓶颈在排序,枚举阶段每个元素最多访问 1 1 1 次,拆分次数最多为 U U U;
- 空间复杂度: O ( l g n ) O(lgn) O(lgn) 排序递归栈空间。
T4. 在传球游戏中最大化函数值(Hard)
https://leetcode.cn/problems/maximize-value-of-function-in-a-ball-passing-game/
题解(树上倍增)
从近期周赛的趋势看,出题人似乎有意想把 LeetCode 往偏竞赛的题目引导。
这道题如果知道树上倍增算法,其实比第三题还简单一些。
- 问题目标: 找到最佳方案,使得从起点开始传球 k k k 次的路径和最大化;
- 暴力: 对于暴力的做法,我们可以枚举以每名玩家为起点的方案,并模拟传球过程求出最佳方案。但是这道题的步长 k k k 的上界非常大 1 0 10 10^{10} 1010,如果逐级向上传球,那么单次查询的时间复杂度是 O ( k ) O(k) O(k)。现在,需要思考如何优化模拟 k k k 次传球的效率;
- 倍增思想: 借鉴 1483. 树节点的第 K 个祖先 的解法,我们可以利用倍增算法将线性的操作施加指数级别的贡献:
- 如果可以预处理出每个玩家的多级后驱玩家,那么在查询时可以加速跳转;
- 由于每个数都可以进行二进制拆分为多个 2 2 2 的幂的和,如果预处理出第 2 0 、 2 1 、 2 2 、 2 3 、 . . . 、 2 i 2^0、2^1、2^2、2^3、...、2^i 20、21、22、23、...、2i 个后驱玩家,那么求解第 k k k 次传球时可以转化为多次 2 i 2^i 2i 个后驱玩家跳转操作,大幅减少操作次数。
class Solution {fun getMaxFunctionValue(receiver: List<Int>, k: Long): Long {val n = receiver.sizeval m = 64 - k.countLeadingZeroBits()// 预处理// dp[i][j] 表示 i 传球 2^j 次后的节点val dp = Array(n) { IntArray(m) }// dp[i][j] 表示 i 传球 2^j 次的路径和val sum = Array(n) { LongArray(m) }for (i in 0 until n) {dp[i][0] = receiver[i]sum[i][0] = receiver[i].toLong()}for (j in 1 until m) {for (i in 0 until n) { // 这道题没有根节点,不需要考虑 child == -1 的情况val child = dp[i][j - 1]// 从 i 条 2^{j-1} 次,再跳 2^{j-1}dp[i][j] = dp[child][j - 1]sum[i][j] = sum[i][j - 1] + sum[child][j - 1]}}// 枚举方案var ret = 0Lfor (node in 0 until n) {var i = nodevar x = kvar s = node.toLong() // 起点的贡献while (x != 0L) {val j = x.countTrailingZeroBits()s += sum[i][j]i = dp[i][j]x = x and (x - 1)}ret = max(ret, s)}return ret}
}
复杂度分析:
- 时间复杂度:预处理时间为 O ( n l g k ) O(nlgk) O(nlgk),枚举时间为 O ( n l g k ) O(nlgk) O(nlgk),其中 n n n 为 r e c e i v e r s receivers receivers 数组的长度;
- 空间复杂度:预处理空间 O ( n l g k ) O(nlgk) O(nlgk)。
另外,这道题还有基于「内向基环树」的 O ( n ) O(n) O(n) 解法。
推荐阅读
LeetCode 上分之旅系列往期回顾:
- LeetCode 单周赛第 359 场 · 结合离散化的线性 DP 问题
- LeetCode 单周赛第 358 场 · 结合中心扩展的单调栈贪心问题
- LeetCode 双周赛第 111 场 · 按部就班地解决动态规划问题
- LeetCode 双周赛第 110 场 · 结合排序不等式的动态规划
⭐️ 永远相信美好的事情即将发生,欢迎加入小彭的 Android 交流社群~

相关文章:

LeetCode 周赛上分之旅 #42 当 LeetCode 考树上倍增,出题的趋势在变化吗
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。 学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度…...
Qt 自定义菜单 托盘菜单
托盘菜单实现:通过QSystemTrayIconQMenuQAction即可完美实现! 实现方式:createActions用于创建菜单、菜单项,translateActions用于设置文本、实现多语化,translateAccount用于设置用户空间配额。 void TrayMenu::createActions(…...

channel并发编程
不要通过共享内存通信,要通过通信共享内存。 channel是golang并发编程中一种重要的数据结构,用于多个goroutine之间进行通信。 我们通常可以把channel想象成一个传送带,将goroutine想象成传送带周边的人,一个传送带的上游放上物品…...

苹果新健康专利:利用 iPhone、Apple Watch 来分析佩戴者的呼吸情况
根据美国商标和专利局(USPTO)公示的清单,苹果获得了一项健康相关的技术专利,可以利用 iPhone、Apple Watch 来分析佩戴者的呼吸系统。 苹果在专利中概述了一种测量用户呼吸功能的系统,通过 iPhone 上的光学感测单元&am…...

数据分析基础-数据可视化02-不同数据类型的可视化概念及原则
将数据空间映射到颜色空间。 数据空间:连续或分类 数据可以被划分为两个主要的数据空间:连续数据和分类数据。这两种数据空间有不同的特点和适用的分析方法。 连续数据(Continuous Data): 连续数据是指可以在某个范…...

QT项目使用Qss的总结
什么是QSS QSS称为Qt Style Sheets也就是Qt样式表,它是Qt提供的一种用来自定义控件外观的机制。QSS大量参考了CSS的内容,只不过QSS的功能比CSS要弱很多,体现在选择器要少,可以使用的QSS属性也要少很多,并且并不是所有…...

suricata初体验+wireshark流量分析
目录 一、suricata介绍 1.下载安装 2.如何使用-攻击模拟 二、wireshark流量分析 1.wireshark过滤器使用 2.wireshark其他使用 一、suricata介绍 1.下载安装 通过官网下载suricata,根据官网步骤进行安装。 官网地址: https://documentation.wazuh.…...

机器学习:异常检测实战
文章目录 Anomaly Detection目录任务介绍数据集方法评估Baseline报告报告评价标准 Anomaly Detection 目录 任务介绍 无监督的异常检测 数据集 方法 autoencode 是否能够还原出原始类型图片,基于重构loss来判断是否正常 重构误差当作异常分数 评估 采用ROC和AUC…...
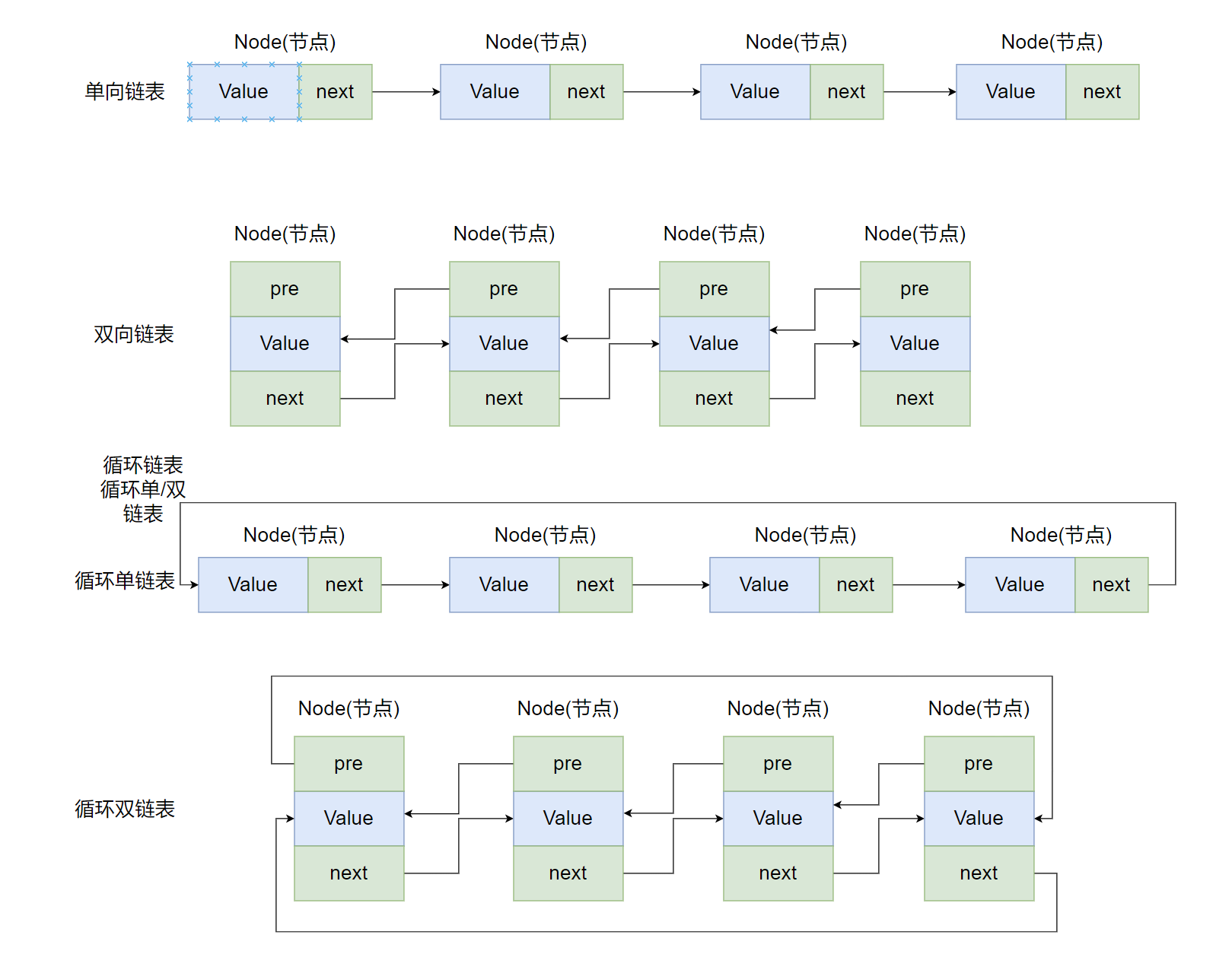
数据结构1
数据结构是计算机科学中存储和组织数据的一种方式,它定义了数据的表示方式和对数据进行操作的方法,常见的数据结构包括数组、栈、链表、队列、树、图等。 目录 一、常见的数据结构 1.数组 2.栈 3.队列 4.链表 5.树 6.图 一、常见的数据结构 1.数…...
自然语言处理学习笔记(七)————字典树效率改进
目录 1. 首字散列其余二分的字典树 2.双数组字典树 3.AC自动机(多模式匹配) (1)goto表 (2)output表 (3)fail表 4.基于双数组字典树的AC自动机 字典树的数据结构在以上的切分算法中已经很快了&#x…...

forEach和map有什么区别,使用场景?
forEach和map有什么区别,使用场景? 区别什么意思?forEach: 不直接改变原始数组,但可以在回调中更改原始数组。 区别 forEach 和 map 都是数组的常用方法,但它们有不同的目的和用法。下面是它们之间的主要区别以及各自…...

【Spring Boot】SpringBoot完整实现社交网站系统
一个完整的社交网站系统需要涉及到用户登录、发布动态、关注、评论、私信等各方面。这里提供一个简单的实现示例,供参考。 前端代码 前端使用Vue框架,以下是部分代码示例: 登录页: <template><div><input type…...

Modbus转Profinet网关连接三菱变频器博图快速配置
本案例将分享如何使用兴达易控的modbus转profinet网关(XD-MDPN100)来连接西门子1200系列plc,并实现三菱变频器的485通讯兼容转modbusTCP通信。通过在博图中进行配置,我们可以实现设备之间的连接和通信。 首先,我们需要…...

8.9 【C语言】有关指针的小结
(1)首先要准确理解指针的含义。 &a是变量a的地址,也可称为变量a的指针。 指针变量是存放地址的变量。 指针变量的值是一个地址。 指针变量也称为地址变量,它的值是地址。 (2)在C语言中,…...

WordPress Nginx伪静态规则设置以及二级目录规则
WordPress Nginx伪静态规则设置以及二级目录规则(wordpress不是安装在根目录的情况) 根目录下WordPress的伪静态规则: location / {if (-f $request_filename/index.html){rewrite (.*) $1/index.html break;}if (-f $request_filename/ind…...

2023年高教社杯 国赛数学建模思路 - 复盘:人力资源安排的最优化模型
文章目录 0 赛题思路1 描述2 问题概括3 建模过程3.1 边界说明3.2 符号约定3.3 分析3.4 模型建立3.5 模型求解 4 模型评价与推广5 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 描述 …...

React内置函数之startTransition与useTransition
React内置函数之startTransition,useTransition 在React中,使用startTransition和useTransition这两个内置函数可以帮助我们更好地管理组件的过渡状态。这两个函数的出现,旨在提供一种简单而强大的方式,来处理组件状态的变化&…...

观察者模式简介
概念: 观察者模式(Observer Pattern)是一种行为型设计模式,用于在对象之间建立一对多的依赖关系,当一个对象的状态发生变化时,其相关依赖对象会自动收到通知并进行相应处理。 特点: 松耦合&a…...

统计程序两个点之间执行的指令数量
环境:支持perf ubuntu安装 apt-get install linux-tools-common linux-tools-generic linux-tools-uname -randroid 一般自带simpleperf 分析 两个点作差, 求中间结果; *(int*)nullptr 0;案例 断点 1 代码 #define SETPOINT(...) do { *(int*)nullptr 0; } while(0…...

时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)
时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价) 目录 时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Matlab实现基于TSO-XGBoost金枪鱼算…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
