Unity 之 Start 与Update 方法的区别
文章目录

当谈论Unity中的
Start和 Update方法时,我们实际上是在讨论MonoBehaviour类中的两个常用方法,用于编写游戏逻辑。这两个方法在不同的时机被调用,因此您可以根据需要选择在哪个方法中编写特定的代码。
Start 方法:
Start方法在脚本所附加的游戏对象被激活后,仅会在第一帧渲染之前被调用一次。它适用于进行一次性的初始化设置和准备工作。如果游戏对象被多次禁用再激活,Start方法仍然只会在首次激活时被调用。
适用场景:
- 在
Start方法中,您可以进行一次性的初始化操作,例如获取其他组件的引用、设置初始位置、加载资源等。 - 如果您的脚本需要与其他对象交互,或者需要在游戏启动时进行特定的设置,那么将这些逻辑放在
Start方法中是很合适的。
示例:
using UnityEngine;public class ExampleScript : MonoBehaviour
{void Start(){Debug.Log("Start method called.");// 在这里进行初始化设置,只会执行一次}void Update(){// 在每帧渲染时处理逻辑}
}
Update 方法:
Update方法在每一帧渲染时调用,通常用于处理与游戏帧同步相关的逻辑。它是一个非常频繁被调用的方法。
适用场景:
- 在
Update方法中,您可以处理与每帧相关的逻辑,例如移动角色、处理输入、更新游戏状态等。 - 如果需要在游戏运行时实时监控用户输入或者更新与时间相关的逻辑,那么将这些代码放在
Update方法中是很合适的。
示例:
using UnityEngine;public class ExampleScript : MonoBehaviour
{void Update(){// 在每帧渲染时处理逻辑// 移动角色、处理输入、更新游戏状态等}
}
通过了解 Start 和 Update 方法的不同用途和调用时机,您可以更好地根据需要在适当的时机编写游戏逻辑,从而实现所需的行为和效果。请注意,在使用 Update 方法时,要注意避免性能问题,尤其是避免在每一帧中执行过多计算或频繁的资源加载。
相关文章:

Unity 之 Start 与Update 方法的区别
文章目录 当谈论Unity中的 Start和 Update方法时,我们实际上是在讨论MonoBehaviour类中的两个常用方法,用于编写游戏逻辑。这两个方法在不同的时机被调用,因此您可以根据需要选择在哪个方法中编写特定的代码。 Start 方法: Start…...

Spring Boot中如何编写优雅的单元测试
单元测试是指对软件中的最小可测试单元进行检查和验证。在Java中,单元测试的最小单元是类。通过编写针对类或方法的小段代码,来检验被测代码是否符合预期结果或行为。执行单元测试可以帮助开发者验证代码是否正确实现了功能需求,以及是否能够…...
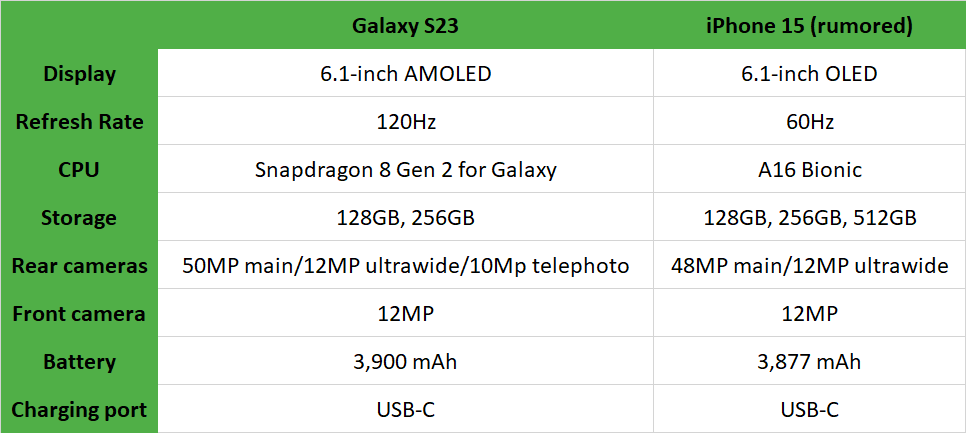
三星Galaxy S23与iPhone 15的对比分析:谁会胜出?
三星Galaxy S23与iPhone 15的对决将于下个月进入高潮,这将是今年智能手机中最大的一场较量。毕竟,这是两家领先的移动设备制造商的旗舰手机。他们的手机的比较将在很大程度上决定谁能获得最佳手机的称号。 我们已经知道有利于三星Galaxy S23的情况,该产品自春季以来一直在推…...

MySQL索引 事物 存储引擎
一 索引 索引的概念 索引就是一种帮助系统能够更快速的查找信息的结构 索引的作用 索引的副作用 创建索引的规则 MySQL的优化 哪些字段/场景适合创建索引 哪些不适合 小字段唯一性强的字段更新不频繁,但查询率比较高的字段表记录超过 300行主键,外键…...

【谷粒学院】报错记录
无法从Nacos获取动态配置 原先gulimall-common中SpringCloud Alibaba的版本是2.1.0.RELEASE,无法从Nacos中获取配置文件信息 <dependencyManagement><dependencies><dependency><groupId>com.alibaba.cloud</groupId><artifactId&…...

微积分基本概念
微分 函数的微分是指对函数的局部变化的一种线性描述。微分可以近似地描述当函数自变量的取值作足够小的改变时,函数的值是怎样改变的。。对于函数 y f ( x ) y f(x) yf(x) 的微分记作: d y f ′ ( x ) d x d_y f^{}(x)d_x dyf′(x)dx 微分和…...
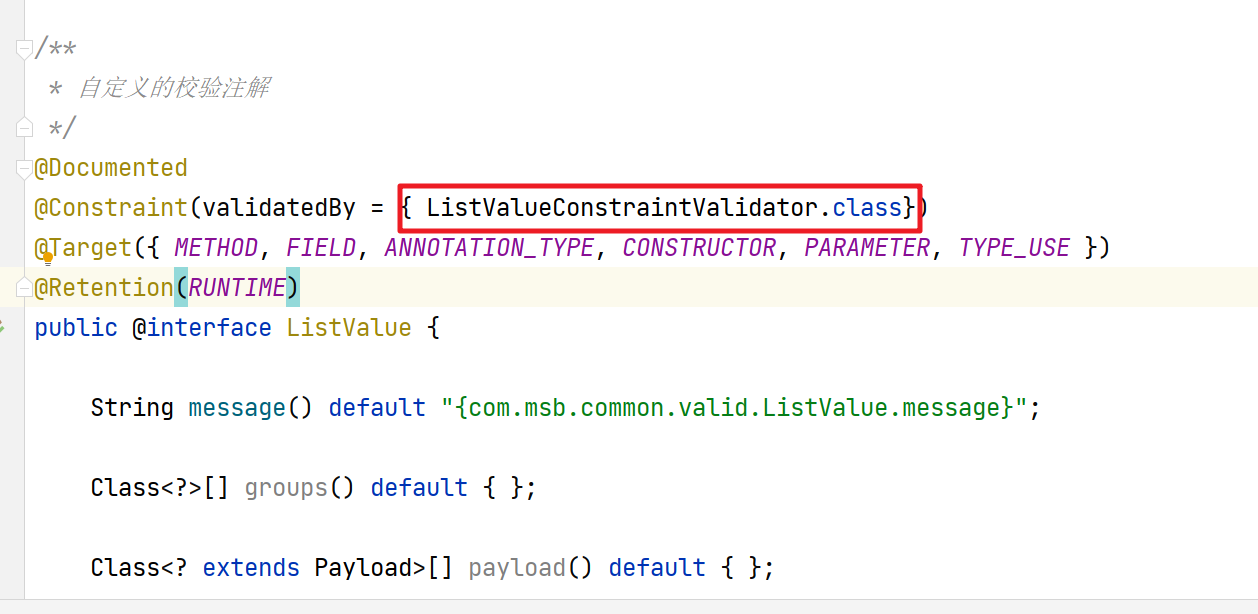
【业务功能篇78】微服务-前端后端校验- 统一异常处理-JSR-303-validation注解
5. 前端校验 我们在前端提交的表单数据,我们也是需要对提交的数据做相关的校验的 Form 组件提供了表单验证的功能,只需要通过 rules 属性传入约定的验证规则,并将 Form-Item 的 prop 属性设置为需校验的字段名即可 校验的页面效果 前端数据…...

pytorch的用法
...

Qt 设置窗口背景
窗口背景无非两种:背景色、背景图片。Qt中窗口背景如何设置? 一、QPalette设置背景 二、实现paintEvent,使用QPainter来绘制背景 三、使用QSS来设置背景 关于QSS的使用不想多说,一般我不用QSS设置窗口背景,也不建议…...

大模型是什么?泰迪大模型能够解决企业哪些痛点?
什么是大模型? 大模型是指模型具有庞大的参数规模和复杂程度的机器学习模型。在深度学习领域,大模型通常是指具有数百万到数十亿参数的神经网络模型。这些模型需要大量的计算资源和存储空间来训练和存储,并且往往需要进行分布式计算和特殊…...

YOLOv7-tracker 目标追踪 输入视频帧
目录 1 项目安装1.1 环境搭建1.2 项目下载1.3 权重下载1.4 环境安装1.5 上传待检测的视频帧 2 视频帧检测与追踪2.1 检测与追踪2.3 结果 参考项目:https://github.com/JackWoo0831/Yolov7-tracker/tree/master github链接:https://github.com/Whiffe/Yo…...

C语言二——C语言编写一段代码,求一元二次方程的根
这段代码实现了解一元二次方程的根的计算。用户需要输入方程的系数a、b、c,然后根据判别式的值确定方程的根的情况,并进行相应的输出。 如果判别式大于0,说明方程有两个实根,分别计算并输出。如果判别式等于0,说明方程…...
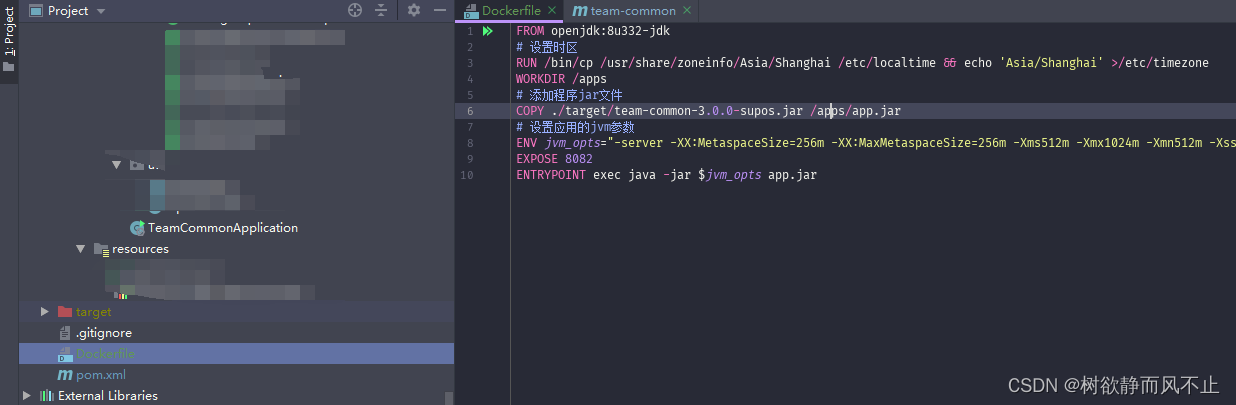
用Idea把SpringBoot项目打包镜像上传至docker
1、设置docker把2375端口开起来 命令查看docker装在哪里 vim docker.service 新增 -H tcp://0.0.0.0:2375 -H unix://var/run/docker.sock 2、配置Dockerfile 我在跟pom同一层 3、配置docker-maven-plugin <plugin><groupId>com.spotify</groupId><arti…...

基于 SVG 的图形交互方案实践
不知道从什么时候起,人们开始喜欢上数字大屏这种“花里胡哨”的东西,仿佛只要用上“科技蓝”这样神奇的色调,就可以让一家公司焕然一新,瞬间变得科技感满满。不管数字大屏的实际意义,是用来帮助企业监控和决策…...

微服务(rpc)
微服务(rpc) 微服务必备的模块生产者消费者管理平台流量控制集群情况下如何做到流量监控 负载均衡服务发现和治理序列化传输序列化和反序列化 微服务是一种架构风格,将一个应用程序拆分为一组小型、独立的服务,每个服务都可以独立…...
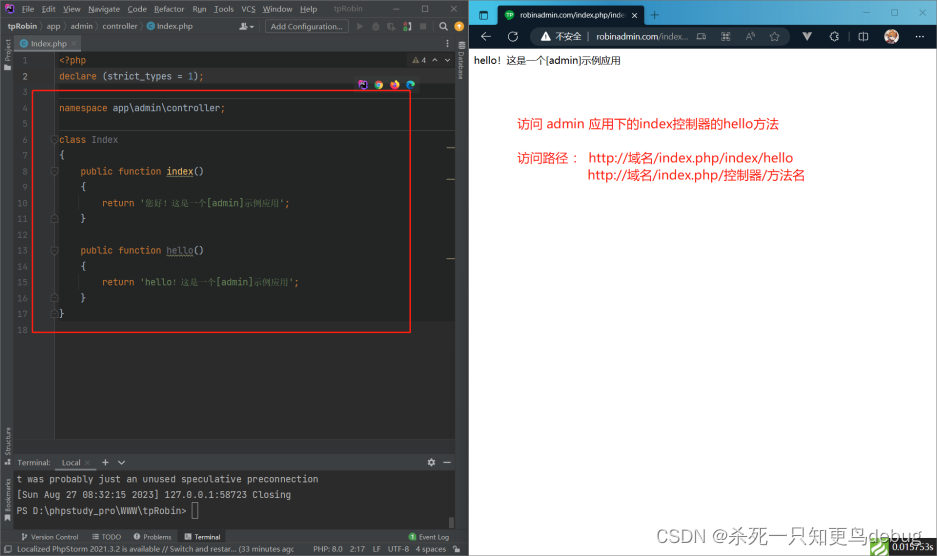
ThinkPHP 多应用配置,及不同域名访问不同应用的配置【详解】
ThinkPHP 多应用配置,及不同域名访问不同应用的配置【详解】 一、安装多应用扩展二、删除项目的中默认的controller文件夹三、创建多应用四、修改config/app.php文件五、测试并且访问多应用六、配置小皮,不同域名访问不同的应用七、小结 一、安装多应用扩…...

Springboot+Mybatis框架是否会取代SSM框架?
个人认真思考的观点:从市场使用来说,会有这个趋势。从技术上来说,不存在被替代这一说。 Spring BootMybatis框架是指使用Spring Boot作为基础框架,并集成Mybatis作为持久层框架的组合,它是一个基于Spring框架的快速开发…...

使用windeployqt和InstallShield打包发布Qt软件的流程
前言 Qt编译之后需要打包发布,并且发布给用户后需要增加一个安装软件,通过安装软件可以实现Qt软件的安装;用于安装软件的软件有很多,这里主要介绍InstallShield使用的流程; 使用windeployqt打包Qt编译后的程序 Qt程序…...
方法阻塞问题)
解决selenium的getdrive()方法阻塞问题
selenium里面的Webdriver的get()方法默认是阻塞的,也就是说要等整个页面全都加载完它才会相应。但我们大部分时候不需要用到页面里的所有东西,也许只需要用到里面的一个元素就行了 所以下面是我的解决方法: 初始化代码: # 设置…...

js的闭包
闭包是有权限访问其他函数作用域的局部变量的一个函数 代码 function outer(){const a1;function f(){console.log(a)}f()}outer() 简单来说:闭包内层函数引用的外层函数变量 为什么要使用闭包? 用此方法可以来统计函数调用次数, 但是如…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
