手写数字识别之网络结构
目录
手写数字识别之网络结构
数据处理
经典的全连接神经网络
卷积神经网络
手写数字识别之网络结构
无论是牛顿第二定律任务,还是房价预测任务,输入特征和输出预测值之间的关系均可以使用“直线”刻画(使用线性方程来表达)。但手写数字识别任务的输入像素和输出数字标签之间的关系显然不是线性的,甚至这个关系复杂到我们靠人脑难以直观理解的程度。

图1:数字识别任务的输入和输出不是线性关系
因此,我们需要尝试使用其他更复杂、更强大的网络来构建手写数字识别任务,观察一下训练效果,即将“横纵式”教学法从横向展开,如 图2 所示。本节主要介绍两种常见的网络结构:经典的多层全连接神经网络和卷积神经网络。

图2:“横纵式”教学法 — 网络结构优化
数据处理
#数据处理部分之前的代码,保持不变
import os
import random
import paddle
import numpy as np
import matplotlib.pyplot as plt
from PIL import Imageimport gzip
import json# 定义数据集读取器
def load_data(mode='train'):# 加载数据datafile = './work/mnist.json.gz'print('loading mnist dataset from {} ......'.format(datafile))data = json.load(gzip.open(datafile))print('mnist dataset load done')# 读取到的数据区分训练集,验证集,测试集train_set, val_set, eval_set = data# 数据集相关参数,图片高度IMG_ROWS, 图片宽度IMG_COLSIMG_ROWS = 28IMG_COLS = 28if mode == 'train':# 获得训练数据集imgs, labels = train_set[0], train_set[1]elif mode == 'valid':# 获得验证数据集imgs, labels = val_set[0], val_set[1]elif mode == 'eval':# 获得测试数据集imgs, labels = eval_set[0], eval_set[1]else:raise Exception("mode can only be one of ['train', 'valid', 'eval']")#校验数据imgs_length = len(imgs)assert len(imgs) == len(labels), \"length of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(labels))# 定义数据集每个数据的序号, 根据序号读取数据index_list = list(range(imgs_length))# 读入数据时用到的batchsizeBATCHSIZE = 100# 定义数据生成器def data_generator():if mode == 'train':random.shuffle(index_list)imgs_list = []labels_list = []for i in index_list:img = np.array(imgs[i]).astype('float32')label = np.array(labels[i]).astype('float32')# 在使用卷积神经网络结构时,uncomment 下面两行代码img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')label = np.reshape(labels[i], [1]).astype('float32')imgs_list.append(img) labels_list.append(label)if len(imgs_list) == BATCHSIZE:yield np.array(imgs_list), np.array(labels_list)imgs_list = []labels_list = []# 如果剩余数据的数目小于BATCHSIZE,# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batchif len(imgs_list) > 0:yield np.array(imgs_list), np.array(labels_list)return data_generator经典的全连接神经网络
经典的全连接神经网络来包含四层网络:输入层、两个隐含层和输出层,将手写数字识别任务通过全连接神经网络表示,如 图3 所示。

图3:手写数字识别任务的全连接神经网络结构
- 输入层:将数据输入给神经网络。在该任务中,输入层的尺度为28×28的像素值。
- 隐含层:增加网络深度和复杂度,隐含层的节点数是可以调整的,节点数越多,神经网络表示能力越强,参数量也会增加。在该任务中,中间的两个隐含层为10×10的结构,通常隐含层会比输入层的尺寸小,以便对关键信息做抽象,激活函数使用常见的Sigmoid函数。
- 输出层:输出网络计算结果,输出层的节点数是固定的。如果是回归问题,节点数量为需要回归的数字数量。如果是分类问题,则是分类标签的数量。在该任务中,模型的输出是回归一个数字,输出层的尺寸为1。
说明:
隐含层引入非线性激活函数Sigmoid是为了增加神经网络的非线性能力。
举例来说,如果一个神经网络采用线性变换,有四个输入x1x_1x1~x4x_4x4,一个输出yyy。假设第一层的变换是z1=x1−x2z_1=x_1-x_2z1=x1−x2和z2=x3+x4z_2=x_3+x_4z2=x3+x4,第二层的变换是y=z1+z2y=z_1+z_2y=z1+z2,则将两层的变换展开后得到y=x1−x2+x3+x4y=x_1-x_2+x_3+x_4y=x1−x2+x3+x4。也就是说,无论中间累积了多少层线性变换,原始输入和最终输出之间依然是线性关系。
Sigmoid是早期神经网络模型中常见的非线性变换函数,通过如下代码,绘制出Sigmoid的函数曲线。
def sigmoid(x):# 直接返回sigmoid函数return 1. / (1. + np.exp(-x))# param:起点,终点,间距
x = np.arange(-8, 8, 0.2)
y = sigmoid(x)
plt.plot(x, y)
plt.show()
<Figure size 432x288 with 1 Axes>
针对手写数字识别的任务,网络层的设计如下:
- 输入层的尺度为28×28,但批次计算的时候会统一加1个维度(大小为batch size)。
- 中间的两个隐含层为10×10的结构,激活函数使用常见的Sigmoid函数。
- 与房价预测模型一样,模型的输出是回归一个数字,输出层的尺寸设置成1。
下述代码为经典全连接神经网络的实现。完成网络结构定义后,即可训练神经网络。
import paddle.nn.functional as F
from paddle.nn import Linear# 定义多层全连接神经网络
class MNIST(paddle.nn.Layer):def __init__(self):super(MNIST, self).__init__()# 定义两层全连接隐含层,输出维度是10,当前设定隐含节点数为10,可根据任务调整self.fc1 = Linear(in_features=784, out_features=10)self.fc2 = Linear(in_features=10, out_features=10)# 定义一层全连接输出层,输出维度是1self.fc3 = Linear(in_features=10, out_features=1)# 定义网络的前向计算,隐含层激活函数为sigmoid,输出层不使用激活函数def forward(self, inputs):# inputs = paddle.reshape(inputs, [inputs.shape[0], 784])outputs1 = self.fc1(inputs)outputs1 = F.sigmoid(outputs1)outputs2 = self.fc2(outputs1)outputs2 = F.sigmoid(outputs2)outputs_final = self.fc3(outputs2)return outputs_final卷积神经网络
虽然使用经典的全连接神经网络可以提升一定的准确率,但其输入数据的形式导致丢失了图像像素间的空间信息,这影响了网络对图像内容的理解。对于计算机视觉问题,效果最好的模型仍然是卷积神经网络。卷积神经网络针对视觉问题的特点进行了网络结构优化,可以直接处理原始形式的图像数据,保留像素间的空间信息,因此更适合处理视觉问题。
卷积神经网络由多个卷积层和池化层组成,如 图4 所示。卷积层负责对输入进行扫描以生成更抽象的特征表示,池化层对这些特征表示进行过滤,保留最关键的特征信息。

图4:在处理计算机视觉任务中大放异彩的卷积神经网络
两层卷积和池化的神经网络实现如下所示。
# 定义 SimpleNet 网络结构
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):def __init__(self):super(MNIST, self).__init__()# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层,池化核的大小kernel_size为2,池化步长为2self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层,池化核的大小kernel_size为2,池化步长为2self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)# 定义一层全连接层,输出维度是1self.fc = Linear(in_features=980, out_features=1)# 定义网络前向计算过程,卷积后紧接着使用池化层,最后使用全连接层计算最终输出# 卷积层激活函数使用Relu,全连接层不使用激活函数def forward(self, inputs):x = self.conv1(inputs)x = F.relu(x)x = self.max_pool1(x)x = self.conv2(x)x = F.relu(x)x = self.max_pool2(x)x = paddle.reshape(x, [x.shape[0], -1])x = self.fc(x)return x使用MNIST数据集训练定义好的卷积神经网络,如下所示。
说明:
以上数据加载函数load_data返回一个数据迭代器train_loader,该train_loader在每次迭代时的数据shape为[batch_size, 784],因此需要将该数据形式reshape为图像数据形式[batch_size, 1, 28, 28],其中第二维代表图像的通道数(在MNIST数据集中每张图片的通道数为1,传统RGB图片通道数为3)。
#网络结构部分之后的代码,保持不变
def train(model):model.train()#调用加载数据的函数,获得MNIST训练数据集train_loader = load_data('train')# 使用SGD优化器,learning_rate设置为0.01opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())# 训练5轮EPOCH_NUM = 10# MNIST图像高和宽IMG_ROWS, IMG_COLS = 28, 28loss_list = []for epoch_id in range(EPOCH_NUM):for batch_id, data in enumerate(train_loader()):#准备数据images, labels = dataimages = paddle.to_tensor(images)labels = paddle.to_tensor(labels)#前向计算的过程predicts = model(images)#计算损失,取一个批次样本损失的平均值loss = F.square_error_cost(predicts, labels)avg_loss = paddle.mean(loss)#每训练200批次的数据,打印下当前Loss的情况if batch_id % 200 == 0:loss = avg_loss.numpy()[0]loss_list.append(loss)print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, loss))#后向传播,更新参数的过程avg_loss.backward()# 最小化loss,更新参数opt.step()# 清除梯度opt.clear_grad()#保存模型参数paddle.save(model.state_dict(), 'mnist.pdparams')return loss_listmodel = MNIST()
loss_list = train(model)loading mnist dataset from ./work/mnist.json.gz ...... mnist dataset load done epoch: 0, batch: 0, loss is: 25.196237564086914 epoch: 0, batch: 200, loss is: 2.8643529415130615 epoch: 0, batch: 400, loss is: 2.0646779537200928 epoch: 1, batch: 0, loss is: 3.135349988937378 epoch: 1, batch: 200, loss is: 2.058072090148926 epoch: 1, batch: 400, loss is: 2.080343723297119 epoch: 2, batch: 0, loss is: 1.9587202072143555 epoch: 2, batch: 200, loss is: 1.6729546785354614 epoch: 2, batch: 400, loss is: 1.7185478210449219 epoch: 3, batch: 0, loss is: 1.4882879257202148 epoch: 3, batch: 200, loss is: 1.239805817604065 epoch: 3, batch: 400, loss is: 1.5459805727005005 epoch: 4, batch: 0, loss is: 2.2185895442962646 epoch: 4, batch: 200, loss is: 1.598059058189392 epoch: 4, batch: 400, loss is: 1.8100342750549316 epoch: 5, batch: 0, loss is: 1.324904441833496 epoch: 5, batch: 200, loss is: 1.1214401721954346 epoch: 5, batch: 400, loss is: 1.9421234130859375 epoch: 6, batch: 0, loss is: 1.0814441442489624 epoch: 6, batch: 200, loss is: 1.5564398765563965 epoch: 6, batch: 400, loss is: 0.9601972699165344 epoch: 7, batch: 0, loss is: 1.287195086479187 epoch: 7, batch: 200, loss is: 1.1438658237457275 epoch: 7, batch: 400, loss is: 1.0299162864685059 epoch: 8, batch: 0, loss is: 1.0495307445526123 epoch: 8, batch: 200, loss is: 1.5844645500183105 epoch: 8, batch: 400, loss is: 0.9159772992134094 epoch: 9, batch: 0, loss is: 0.8777803778648376 epoch: 9, batch: 200, loss is: 1.1280484199523926 epoch: 9, batch: 400, loss is: 1.1104599237442017
可视化损失变化:
def plot(loss_list):plt.figure(figsize=(10,5))freqs = [i for i in range(len(loss_list))]# 绘制训练损失变化曲线plt.plot(freqs, loss_list, color='#e4007f', label="Train loss")# 绘制坐标轴和图例plt.ylabel("loss", fontsize='large')plt.xlabel("freq", fontsize='large')plt.legend(loc='upper right', fontsize='x-large')plt.show()plot(loss_list)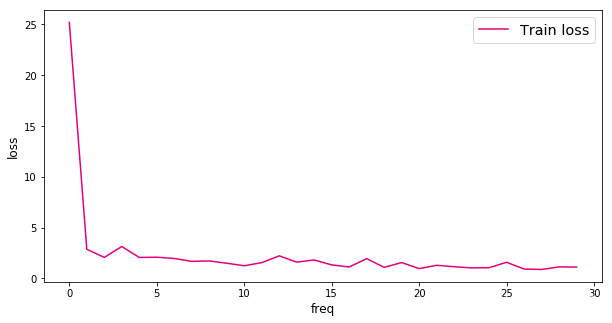
<Figure size 720x360 with 1 Axes>
比较经典全连接神经网络和卷积神经网络的损失变化,可以发现卷积神经网络的损失值下降更快,且最终的损失值更小。
相关文章:

手写数字识别之网络结构
目录 手写数字识别之网络结构 数据处理 经典的全连接神经网络 卷积神经网络 手写数字识别之网络结构 无论是牛顿第二定律任务,还是房价预测任务,输入特征和输出预测值之间的关系均可以使用“直线”刻画(使用线性方程来表达)…...

《动手深度学习》 线性回归从零开始实现实例
🎈 作者:Linux猿 🎈 简介:CSDN博客专家🏆,华为云享专家🏆,Linux、C/C、云计算、物联网、面试、刷题、算法尽管咨询我,关注我,有问题私聊! &…...

Redis 命令
Redis 命令 Redis 命令用于在 redis 服务上执行操作。 要在 redis 服务上执行命令需要一个 redis 客户端。Redis 客户端在我们之前下载的的 redis 的安装包中。 语法 Redis 客户端的基本语法为: $ redis-cli实例 以下实例讲解了如何启动 redis 客户端…...
Linux网络编程:线程池并发服务器 _UDP客户端和服务器_本地和网络套接字
文章目录: 一:线程池模块分析 threadpool.c 二:UDP通信 1.TCP通信和UDP通信各自的优缺点 2.UDP实现的C/S模型 server.c client.c 三:套接字 1.本地套接字 2.本地套 和 网络套对比 server.c client.c 一:线…...
nvm安装electron开发与编译环境
electron总是安装失败,下面说一下配置办法 下载软件 nvm npmmirror 镜像站 安装nvm 首先最好卸载node,不卸载的话,安装nvm会提示是否由其接管,保险起见还是卸载 下载win中的安装包 配置加速节点nvm node_mirror https://npmmi…...

玩转Mysql系列 - 第7篇:玩转select条件查询,避免采坑
这是Mysql系列第7篇。 环境:mysql5.7.25,cmd命令中进行演示。 电商中:我们想查看某个用户所有的订单,或者想查看某个用户在某个时间段内所有的订单,此时我们需要对订单表数据进行筛选,按照用户、时间进行…...

启动程序结束程序打开指定网页
import subprocess subprocess.Popen(r"C:\\Program Files\\5EClient\\5EClient.exe") # 打开指定程序 import os os.system(TASKKILL /F /IM notepad.exe) # 结束指定程序 import webbrowser webbrowser.open_new_tab(https://www.baidu.com) # 打开指定网页...
)
从零开始学习 Java:简单易懂的入门指南之包装类(十九)
包装类 包装类5.1 概述5.2 Integer类5.3 装箱与拆箱5.4 自动装箱与自动拆箱5.5 基本类型与字符串之间的转换基本类型转换为StringString转换成基本类型 5.6 底层原理 算法小题练习一:练习二:练习三:练习四:练习五: 包装…...
(一、数组交集问题))
leetcode分类刷题:哈希表(Hash Table)(一、数组交集问题)
1、当需要快速判断某元素是否出现在序列中时,就要用到哈希表了。 2、本文针对的总结题型为给定两个及多个数组,求解它们的交集。接下来,按照由浅入深层层递进的顺序总结以下几道题目。 3、以下题目需要共同注意的是:对于两个数组&…...
UML四大关系
文章目录 引言UML的定义和作用UML四大关系的重要性和应用场景关联关系继承关系聚合关系组合关系 UML四大关系的进一步讨论UML四大关系的实际应用软件开发中的应用其他领域的应用 总结 引言 在软件开发中,统一建模语言(Unified Modeling Language&#x…...
、三种页面的渲染方式、数据校验的使用)、form组件的参数以及单选多选形式)
forms组件(钩子函数(局部钩子、全局钩子)、三种页面的渲染方式、数据校验的使用)、form组件的参数以及单选多选形式
一、form是组件 后端代码 from django.shortcuts import render, redirect, HttpResponsedef ab_form(request):back_dict {username: , password: }if request.method POST:username request.POST.get(username)password request.POST.get(password)if 金瓶梅 in userna…...

跨专业申请成功|金融公司经理赴美国密苏里大学访学交流
J经理所学专业与从事工作不符,尽管如此,我们还是为其成功申请到美国密苏里大学经济学专业的访问学者职位,全家顺利过签出国。 J经理背景: 申请类型: 自费访问学者 工作背景: 某金融公司经理 教育背景&am…...
)
第十一章 CUDA的NMS算子实战篇(下篇)
cuda教程目录 第一章 指针篇 第二章 CUDA原理篇 第三章 CUDA编译器环境配置篇 第四章 kernel函数基础篇 第五章 kernel索引(index)篇 第六章 kenel矩阵计算实战篇 第七章 kenel实战强化篇 第八章 CUDA内存应用与性能优化篇 第九章 CUDA原子(atomic)实战篇 第十章 CUDA流(strea…...

R语言01-数据类型
概念 数值型(Numeric):用于存储数值数据,包括整数和浮点数。例如:x <- 5。 字符型(Character):用于存储文本数据,以单引号或双引号括起来。例如:name &l…...
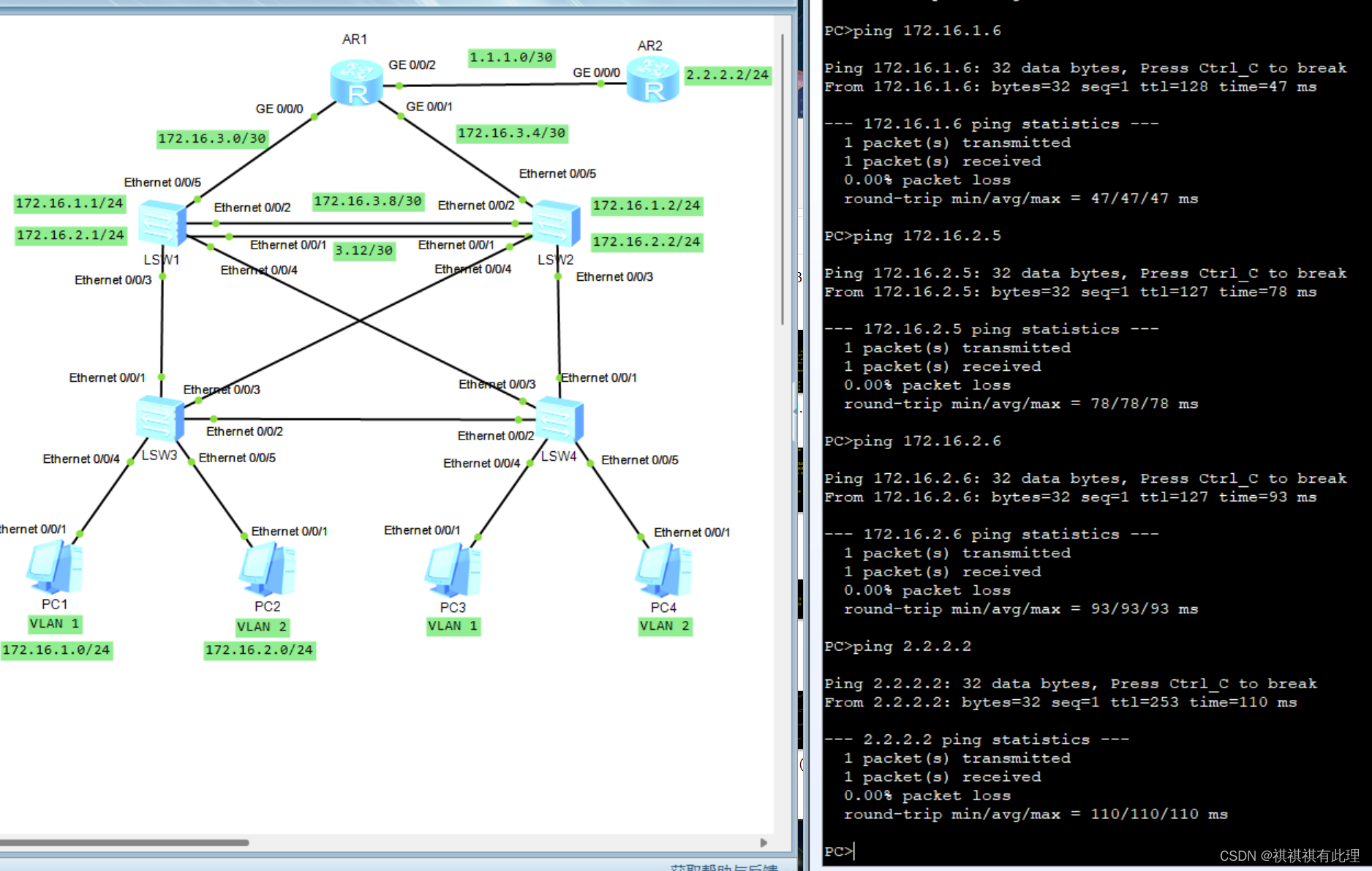
【网络基础实战之路】基于三层架构实现一个企业内网搭建的实战详解
系列文章传送门: 【网络基础实战之路】设计网络划分的实战详解 【网络基础实战之路】一文弄懂TCP的三次握手与四次断开 【网络基础实战之路】基于MGRE多点协议的实战详解 【网络基础实战之路】基于OSPF协议建立两个MGRE网络的实验详解 【网络基础实战之路】基于…...

C++11相较于C++98多了哪些可调用对象?--《包装器》篇
C98里面的可调用对象只有普通函数和函数指针。 而在C11里面可调用的对象有下面几种: 普通函数函数指针仿函数lambda表达式(匿名函数)包装器 普通函数、函数指针、仿函数、lambda表达式我在以前的文章里其实已经介绍过了 包装器 在C11里面有…...

栈与队列:常见的线性数据结构
栈(Stack)和队列(Queue)是计算机科学中常见的线性数据结构,它们在许多算法和编程场景中发挥着重要作用。它们的不同特点和用途使得它们适用于不同的问题和应用。 栈(Stack) 栈,作为…...

android framework之AMS的启动管理与职责
AMS是什么? AMS管理着activity,Service, Provide, BroadcastReceiver android10后:出现ATMS,ActivityTaskManagerService:ATMS是从AMS中抽出来,单独管理着原来AMS中的Activity组件 。 现在我们对AMS的分析,也就包含对…...

Decoupling Knowledge from Memorization: Retrieval-augmented Prompt Learning
本文是LLM系列的文章,针对《Decoupling Knowledge from Memorization: Retrieval 知识与记忆的解耦:检索增强的提示学习 摘要1 引言2 提示学习的前言3 RETROPROMPT:检索增强的提示学习4 实验5 相关实验6 结论与未来工作 摘要 提示学习方法在…...
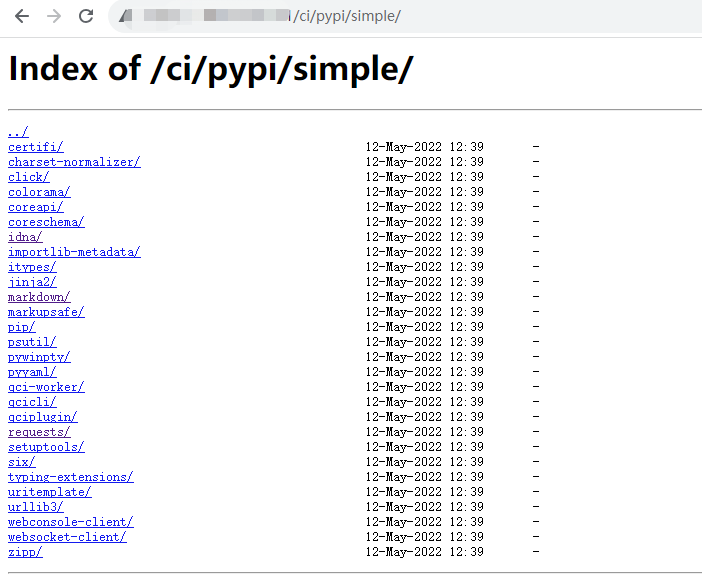
腾讯云coding平台平台inda目录遍历漏洞复现
前言 其实就是一个python的库可以遍历到,并不能遍历到别的路径下,后续可利用性不大,并且目前这个平台私有部署量不多,大多都是用腾讯云在线部署的。 CODING DevOps 是面向软件研发团队的一站式研发协作管理平台,提供…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
