Leetcode 191.位1的个数

编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为汉明重量)。
提示:
- 请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
- 在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在 示例 3 中,输入表示有符号整数
-3。
示例 1:
输入:n = 00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
输入:n = 00000000000000000000000010000000 输出:1 解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
输入:n = 11111111111111111111111111111101 输出:31 解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
提示:
- 输入必须是长度为
32的 二进制串 。
进阶:
- 如果多次调用这个函数,你将如何优化你的算法?
我的答案:
一、信息
1.输入是一个二进制无符号整数
2.返回'1'的个数
二、分析
条件1告诉我输入的数据类型是无符号整型
条件2告诉我此次编程的目标
三、步骤
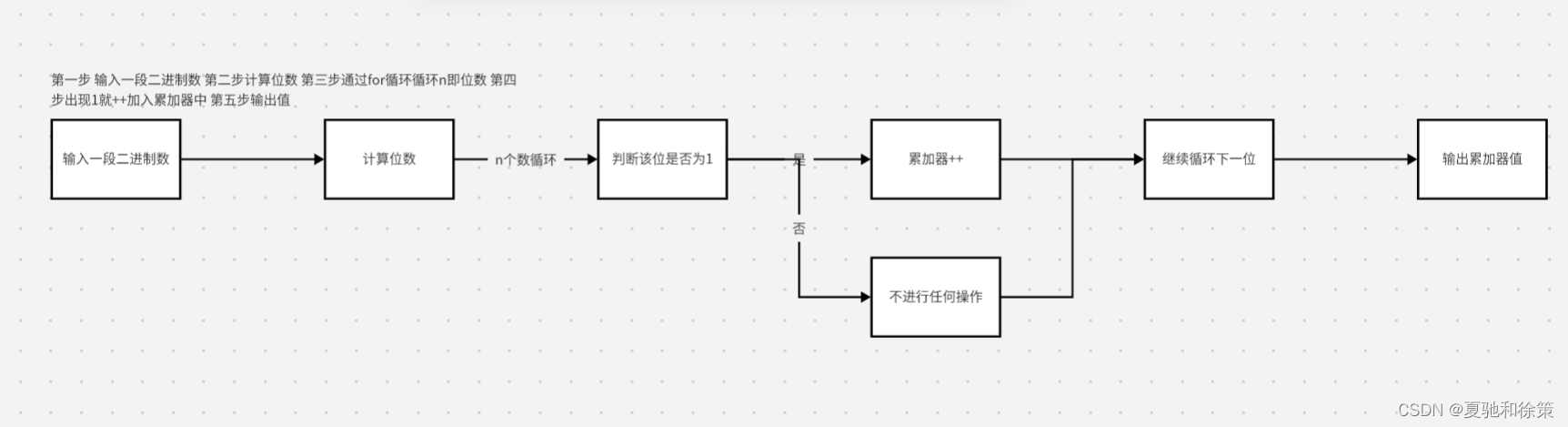
遇到问题
1.如何计算位数?
四、实现
我的答案:
毫无思路
这是一个常见的面试问题。让我们首先为这个问题创建一个C语言的解决方案,然后是一个C++的解决方案。
#include <stdint.h> // for uint32_tint hammingWeight(uint32_t n) {int count = 0;while (n) {count += n & 1;n >>= 1;}return count;
}
C++:
#include <cstdint> // for uint32_tint hammingWeight(uint32_t n) {int count = 0;while (n) {count += n & 1;n >>= 1;}return count;
}
进阶:优化算法
如果要多次调用这个函数,我们可以使用Brian Kernighan的算法,它可以更快地计算二进制中1的个数,它的工作原理是每次迭代都去掉最右边的1,直到所有的1都被去掉。
C语言(进阶)
#include <stdint.h> // for uint32_tint hammingWeight(uint32_t n) {int count = 0;while (n) {n &= (n - 1);count++;}return count;
}
C++(进阶)
#include <cstdint> // for uint32_tint hammingWeight(uint32_t n) {int count = 0;while (n) {n &= (n - 1);count++;}return count;
}
Brian Kernighan的算法的效率是O(k),其中k是二进制数中1的个数,因此对于具有少量1的数字,它的效率非常高。
Leetcode答案
方法一:循环检查二进制位
思路及解法
我们可以直接循环检查给定整数 nnn 的二进制位的每一位是否为 111。
具体代码中,当检查第 iii 位时,我们可以让 nnn 与 2i2^i2
i
进行与运算,当且仅当 nnn 的第 iii 位为 111 时,运算结果不为 000。
代码
C++
class Solution {
public:int hammingWeight(uint32_t n) {int ret = 0;for (int i = 0; i < 32; i++) {if (n & (1 << i)) {ret++;}}return ret;}
};
复杂度分析
时间复杂度:O(k)O(k)O(k),其中 kkk 是 int\texttt{int}int 型的二进制位数,k=32k=32k=32。我们需要检查 nnn 的二进制位的每一位,一共需要检查 323232 位。
空间复杂度:O(1)O(1)O(1),我们只需要常数的空间保存若干变量。
方法二:位运算优化
思路及解法
观察这个运算:n & (n−1)n~\&~(n - 1)n & (n−1),其运算结果恰为把 nnn 的二进制位中的最低位的 111 变为 000 之后的结果。
如:6 & (6−1)=4,6=(110)2,4=(100)26~\&~(6-1) = 4, 6 = (110)_2, 4 = (100)_26 & (6−1)=4,6=(110)
2
,4=(100)
2
,运算结果 444 即为把 666 的二进制位中的最低位的 111 变为 000 之后的结果。
这样我们可以利用这个位运算的性质加速我们的检查过程,在实际代码中,我们不断让当前的 nnn 与 n−1n - 1n−1 做与运算,直到 nnn 变为 000 即可。因为每次运算会使得 nnn 的最低位的 111 被翻转,因此运算次数就等于 nnn 的二进制位中 111 的个数。
代码
C++
Java
Python3
Golang
JavaScript
C
class Solution {
public:int hammingWeight(uint32_t n) {int ret = 0;while (n) {n &= n - 1;ret++;}return ret;}
};
复杂度分析
时间复杂度:O(logn)O(\log n)O(logn)。循环次数等于 nnn 的二进制位中 111 的个数,最坏情况下 nnn 的二进制位全部为 111。我们需要循环 logn\log nlogn 次。
空间复杂度:O(1)O(1)O(1),我们只需要常数的空间保存若干变量。
链接:https://leetcode.cn/problems/number-of-1-bits/solutions/672082/wei-1de-ge-shu-by-leetcode-solution-jnwf/
来源:力扣(LeetCode)
英雄师傅答案:
int hammingWeight(uint32_t n){int c=0;while(n){if(n&1){++c;}n>>=1;}return c;
}几种方法的比较:
我的方法
1. **Brian Kernighan算法:** 这实际上与你给出的第二种方法相同,即使用`n & (n-1)`技巧。它直接移除了数字中最右侧的'1'。
2. **直接计数:** 这是一个直观的方法。对数字的每一位进行循环,并用`n & 1`检查最低位是否为'1'。之后,右移数字。
### 对比与分析
**1. 循环检查二进制位 vs 直接计数**
- **思路相似性:** 这两种方法都是基于检查每一位来计算'1'的数量。
- **优势:** 这两种方法都是非常直观的。对于初学者或者希望代码具有更高可读性的情境,它们都很适用。
- **劣势:** 它们的性能可能不如位运算优化方法,特别是当原始数字的二进制表示中有较少的'1'时。
**2. 位运算优化 vs Brian Kernighan算法**
- **思路相似性:** 它们实际上是同一种方法。都使用了`n & (n-1)`的技巧来移除数字中的一个'1'。
- **优势:** 它们都比直接计数方法快,尤其是在数字中'1'较少时。
- **劣势:** 对于不熟悉这种特定位运算的人来说,可能不够直观。
### 总结
- 我的"直接计数"方法和你给的"循环检查二进制位"方法非常相似。它们都是基于检查每一位的简单方法。然而,由于涉及到的位移操作,实现的细节可能会有所不同。
- 我的"Brian Kernighan算法"和你给的"位运算优化"方法实际上是同一种方法。这种方法利用了`n & (n-1)`来高效地计算'1'的数量,它比基于逐位检查的方法更快。
无论选择哪种方法,最重要的是理解其背后的逻辑和原理,这样在遇到不同的问题时,你可以灵活地应用和调整这些方法。
总结:
一、发现的不足。
1.运算符>>知识点尤其是移位运算不熟悉
2.
二、学到什么?
从这道题目中,我们可以学到以下几点:
1. **二进制基础**:题目加深了我们对二进制数的理解,特别是如何操作和解读32位无符号整数的二进制形式。
2. **位操作**:题目展示了如何使用位操作符,特别是`&` (位与) 和 `<<` (左移)。位操作是计算机科学中的一个重要概念,特别是在低级编程、嵌入式系统和性能关键应用中。
3. **算法优化**:通过比较两种方法,我们看到了如何从一个直接的算法优化到一个更高效的算法。方法一直接检查每一位,而方法二使用了一个巧妙的技巧,即`n & (n - 1)`,来迅速定位并清除最右侧的`1`。这显示了算法和数据结构知识的重要性,特别是如何使用基础的位操作来优化算法。
4. **代码简洁性和效率**:两种方法都提供了解决同一问题的有效方法,但它们之间的效率有所不同。这强调了在解决问题时不仅要考虑解决方案的正确性,还要考虑其效率。
5. **问题分析与解决策略**:面对一个问题时,首先需要理解其背后的概念和要求,然后尝试提出不同的策略或方法。对于同一个问题,可能存在多种有效的解决策略,但它们在实际应用中的效率可能会有所不同。
6. **细节注意**:在处理位操作时,特别要注意边界条件和位数。例如,对于32位的整数,当我们移动超过32位时,需要注意可能出现的行为。
综上所述,这道题目为我们提供了一个很好的机会,来学习和实践位操作、算法优化和问题解决策略。

相关文章:

Leetcode 191.位1的个数
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 1 的个数(也被称为汉明重量)。 提示: 请注意,在某些语言(如 Java)中…...
安防监控视频平台EasyCVR视频汇聚平台调用接口出现跨域现象的问题解决方案
视频监控汇聚EasyCVR可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有GB28181、RTSP/Onvif、RTMP等,以及厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等,能对外分发RTSP、RTMP、FLV、HLS、WebRTC等格式的视…...

Python中的一些常用操作
文章目录 一. Python操作之-- 使用Python 提取PDF文件中的表格数据!二:三: Python中的 staticmethodclassmethod方法四: 反斜杠 \五: 终端的解释器提示符号修改六: python使用json.dumps输出中文七…...

go语言调用python脚本
文章目录 代码gopython 在 go语言中调用 python 程序,你可能会用到 代码 亲测 go 测试 go 文件 func TestR(t *testing.T) {// 设置要执行的Python脚本和参数scriptPath : "../nansen.py"arg1 : "nansen"// 执行Python脚本cmd : exec.Comm…...

2.3 【MySQL】命令行和配置文件中启动选项的区别
在命令行上指定的绝大部分启动选项都可以放到配置文件中,但是有一些选项是专门为命令行设计的,比方说defaults-extra-file 、 defaults-file 这样的选项本身就是为了指定配置文件路径的,再放在配置文件中使用就没啥意义了。 如果同一个启动选…...

外部库/lib/maven依赖项 三者关系
外部库(存放项目初始配置的jar包)(它的文件夹里并没有包含lib文件夹的引的外部的依赖的jar包) lib(存放外部导入到项目的依赖的jar包) maven依赖项(管理项目所有的jar包依赖) 三者存放jar包的关系 项目所依赖的全部的jar包 maven依赖项的jar包 外部库中的jar包 lib中的…...
在线制作作息时间表
时光荏苒,岁月如梭,人们描述时光易逝的句子,多如星河。 一寸光阴一寸金,寸金难买寸光阴。 人生就是一段时间而已,所以我明白了一个道理 人生之中最大的浪费就是时间的浪费 因此我想我们教给我们孩子重要的一课应该也是…...

他们朝我扔泥巴(scratch)
前言 纯~~~属~~~虚~~~构~~~(同学看完短视频要我做,蟹蟹你) 用scratch做的,幼稚得嘞( ̄_ ̄|||)呵呵(强颜欢笑) 完成视频 视频试了好久,就是传不上来,私信我加我…...

docker部署前端项目保姆级教程
本地启动docker(有不会启动的吗?下载docker(小海豚)双击起来就行) 准备阿里云账号(免费) 没有就去注册一个,记住密码后面要用到 官网地址:阿里云登录 - 欢迎登录阿里云…...

《C和指针》笔记13: static关键字总结
这里对static关键字做一下总结,可以回顾一下前面两篇博客的文章。 《C和指针》笔记11: external和internal链接属性 《C和指针》笔记12: 存储类型(自动变量、静态变量和寄存器变量) 当它用于函数定义时,或用于代码块之外的变量声…...

Docker harbor私有仓库部署与管理
一、搭建本地私有仓库二、Harbor私有仓库部署与管理1、Harbor概述2、Harbor的特性3、Harbor的核心组件3.1 Proxy3.2 Registry3.3 Core services3.3.1 UI(harbor-ui)3.3.2 WebHook3.3.3 Token 服务 3.4 Database(harbor-db)3.5 Log…...

解锁Selenium的力量:不仅仅是Web测试
Selenium简介 Selenium,作为Web应用测试的领军者,已经成为了无数开发者和测试人员的首选工具。它不仅仅是一个自动化测试工具,更是一个强大的Web应用交互框架。 Selenium的起源与发展 Selenium的历史可以追溯到2004年,由Jason Hu…...
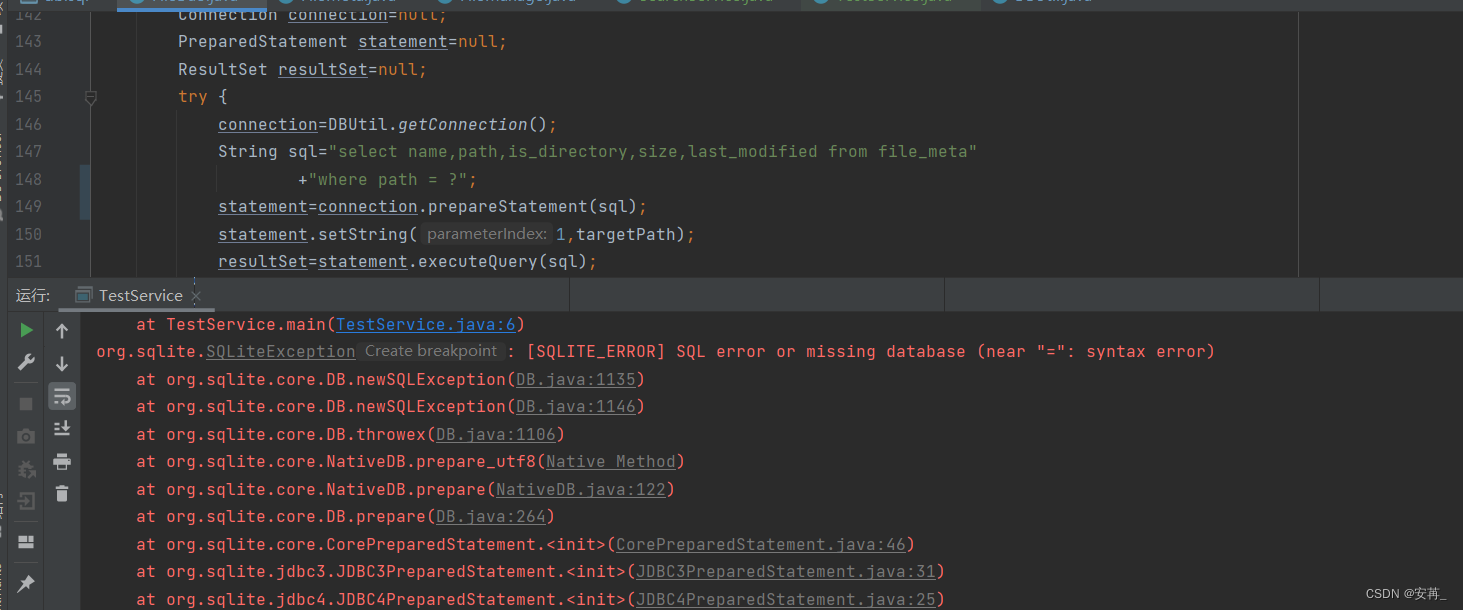
[SQLITE_ERROR] SQL error or missing database (near “=“: syntax error)【已解决】
这个报的错误是语法错误,但是我并没有看出来这行代码有什么错。 通过排除掉下边两个问题解决的 从增加记录方法复制的下来的代码,只删除了关闭自动提交事务,但是connection.commit忘记删除executeQuery和executeUpdate方法的用法忘记了&…...

【视觉系统】笔芯内径机器视觉测量软硬件方案-康耐德智能
检测内容 笔芯内径机器视觉测量系统 检测要求 精度0.03mm,速度120~180个/分钟 视觉可行性分析 对样品进行了光学实验,并进行图像处理,原则上可以使用机器视觉系统进行测试测量。 结果: 对所有样品进行分析,可以在不…...

将文件夹的名称写到Excel中
查看文件夹名称 os.listdir()函数会返回指定路径下的所有文件和文件夹的名称列表,包括隐藏文件和文件夹 import osfolder_path . # 文件夹路径 # . is当前路径 files os.listdir(folder_path) # 获取文件夹内所有文件的名称列表for filename in files:print(fi…...

关于Vue CLI项目 运行发生了 less-lorder错误的解决方案
Module node found :Error: Can’t resolve ‘less-loader’ 报错 文章目录 Module node found :Error: Cant resolve less-loader 报错解决方案:安装 webpack 和 less安装 less-loader 问题: 在运行vue项目的时候发生: Module not found: Er…...

【Qt学习】02:信号和槽机制
信号和槽机制 OVERVIEW 信号和槽机制一、系统自带信号与槽二、自定义信号与槽1.基本使用student.cppteacher.cppwidget.cppmain.cpp 2.信号与槽重载student.cppteacher.cppwidget.cppmain.cpp 3.信号连接信号4.Lambda表达式5.信号与槽总结 信号槽机制是 Qt 框架引以为豪的机制之…...

软件工程(十三) 设计模式之结构型设计模式(一)
前面我们记录了创建型设计模式,知道了通过各种模式去创建和管理我们的对象。但是除了对象的创建,我们还有一些结构型的模式。 1、适配器模式(Adapter) 简要说明 将一个类的接口转换为用户希望得到的另一个接口。它使原本不相同的接口得以协同工作。 速记关键字 转换接…...
Node与Express后端架构:高性能的Web应用服务
在现代Web应用开发中,后端架构的性能和可扩展性至关重要。Node.js作为一个基于事件驱动、非阻塞I/O的平台,以及Express作为一个流行的Node.js框架,共同构建了高性能的Web应用服务。 在本文中,我们将深入探讨Node与Express后端架构…...

C++炸弹小游戏
游戏效果 小人可以随便在一些元素(如石头,岩浆,水,宝石等)上跳跃,“地面”一直在上升,小人上升到顶部或者没有血的时候游戏结束(初始20点血),小人可以随意放炸…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
