当前位置： 首页 > news >正文

origin导出pdf曲线超出边框

news 2026/3/30 18:40:07

软件版本

软件版本
Word2021
Origin2021
Adobe Acrobat Pro2023

问题描述

Origin导出的emf格式矢量图片，插入到Word中，显示正常，但是在使用Word导出→创建Adobe PDF→创建Adobe PDF导出PDF文件后，图片曲线就会超出边框，如下图所示

Word中展示效果                                导出的PDF中效果

原因分析

那是因为横坐标区间不是采样周期的整数倍，也就是PDF自动将下一个采样点对应的中间曲线显示了出来。

解决方案

修改横坐标范围即可

相关文章：

origin导出pdf曲线超出边框

软件版本 软件版本Word2021Origin2021Adobe Acrobat Pro2023 问题描述 Origin导出的emf格式矢量图片，插入到Word中，显示正常，但是在使用Word导出→创建Adobe PDF→创建Adobe PDF导出PDF文件后，图片曲线就会超出边框&#xff0c…...

编程日记 2023/8/29 19:14:10

由Android10适配到Android12时遇到相关编译失败问题

最近Android系统各大应用商店联合发出公告，处于个人隐私安全考虑，强制APP适配到Android 11及以上版本。下面是其中应用市场的公告（顺带提醒没适配的同学）： 适配前的开发环境 名称版本Android studioGiraffe | 2022.3…...

编程日记 2023/8/29 19:13:08

高职教育应对ChatGPT应用的策略

一、完善顶层设计，提升技术水平 在推广ChatGPT平台的过程中，高职院校需要关注技术本身的问题。这就需要在国家和地方政府的引导下，引入更完善的技术顶层设计，提高人工智能在高职教育中的运用水平。具体来说，一方面需要…...

编程日记 2023/8/29 19:12:07

Linux 内核编译参数

文章目录 前言1 -Wall2 -Wundef3 -Wstrict-prototypes4 -Wno-trigraphs5 -fno-strict-aliasing6 -fno-common7 -Werror-implicit-function-declaration8 -Wno-format-security9 -fno-delete-null-pointer-checks10 -stdgnu89 前言 # cat /etc/os-release NAME"CentOS Lin…...

编程日记 2023/8/29 19:11:06

vscode使用anaconda自带的python环境在终端运行时报错

目录 具体报错内容官方翻译报错讲人话解决方法 具体报错内容 CommandNotFoundError: Your shell has not been properly configured to use conda activate. If your shell is Bash or a Bourne variant, enable conda for the current user with$ echo ". E:\Anaconda/e…...

编程日记 2023/8/29 19:10:05

葡萄叶病害识别（图像连续识别和视频识别，Python代码，pyTorch框架）

葡萄叶病害识别（图像连续识别和视频识别，Python代码，pyTorch框架）_哔哩哔哩_bilibili 葡萄数据集 第一个文件夹为 Grape Black Measles（葡萄黑麻疹）病害（3783张） Grape Black rot葡…...

编程日记 2023/8/29 19:09:03

Oracle drop删除表如何恢复

摘要： 在 Oracle 数据库管理中，DROP 命令的误操作可能导致数据不可挽回的丢失。然而，Oracle 提供了回收站（recycle bin）功能，允许用户在删除对象后的一段时间内恢复它们。本文将介绍如何查询、启用和管理回…...

编程日记 2023/8/29 19:08:02

5、监测数据采集物联网应用开发步骤(5.1)

监测数据采集物联网应用开发步骤(4) Sqlite3数据库读写操作开发、异常信息统一处理类开发 本章节需要调用sqlite3及mysql-connector 安装sqlite3 Pip3 install sqlite3 安装mysql-connector pip3 install mysql-connector 验证是否安装成功，python中运行下列…...

编程日记 2023/8/29 19:07:00

ZZULIOJ 1148: 组合三位数之一，Java

ZZULIOJ 1148: 组合三位数之一，Java 题目描述 把1、2、3、4、5、6、7、8、9组合成3个3位数，要求每个数字仅使用一次，使每个3位数均为完全平方数。按从小到大的顺序输出这三个三位数。 输入 无 输出 按从小到大的顺序输出这三个三位数&a…...

编程日记 2023/8/29 19:05:59

ROS功能包目录下CMakeLists.txt

1. add_execuble CMake基础教程&#xff08;24&#xff09;add_executable生成目标可执行文件 CMake中add_executable的使用 CMake中的add_executable命令用于使用指定的源文件向项目(project)添加可执行文件&#xff0c;其格式如下&#xff1a; add_executable(<name>…...

编程日记 2023/8/29 19:04:57

Python爬虫追踪新闻事件发展进程及舆论反映

目录 实现方案 1. 确定目标新闻源&#xff1a; 2. 确定关键词&#xff1a; 3. 使用网络爬虫获取新闻内容&#xff1a; 4. 提取和分析新闻文章&#xff1a; 5. 追踪新闻事件的发展进程&#xff1a; 6. 监测舆论反映&#xff1a; 7. 数据可视化&#xff1a; 完整代码示例…...

编程日记 2023/8/29 19:03:56

block层：7. 请求下发

blk_dispatch 源码基于5.10 1. blk_mq_sched_dispatch_requests void blk_mq_sched_dispatch_requests(struct blk_mq_hw_ctx *hctx) {// 队列struct request_queue *q hctx->queue;// 队列已停止或者被暂停if (unlikely(blk_mq_hctx_stopped(hctx) || blk_queue_quiesc…...

编程日记 2023/8/29 19:02:55

Matlab图像处理-平移运算

几何运算 几何运算又称为几何变换&#xff0c;是将一幅图像中的坐标映射到另外一幅图像中的新坐标位置&#xff0c;它不改变图像的像素值&#xff0c;只是改变像素所在的几何位置&#xff0c;使原始图像按照需要产生位置、形状和大小的变化。 图像几何运算的一般定义为&#…...

编程日记 2023/8/29 19:01:54

美创科技一体化智能化公共数据平台数据安全建设实践

公共数据是当今政府数字化转型的关键要素和未来价值释放的核心锚点&#xff0c;也是“网络强国”、“数字中国”的战略性资源。 作为数字化改革先行省份&#xff0c;近年来&#xff0c;浙江省以一体化智能化公共数据平台作为数字化改革的支撑总平台&#xff0c;实现了全省公共数…...

编程日记 2023/8/29 19:00:53

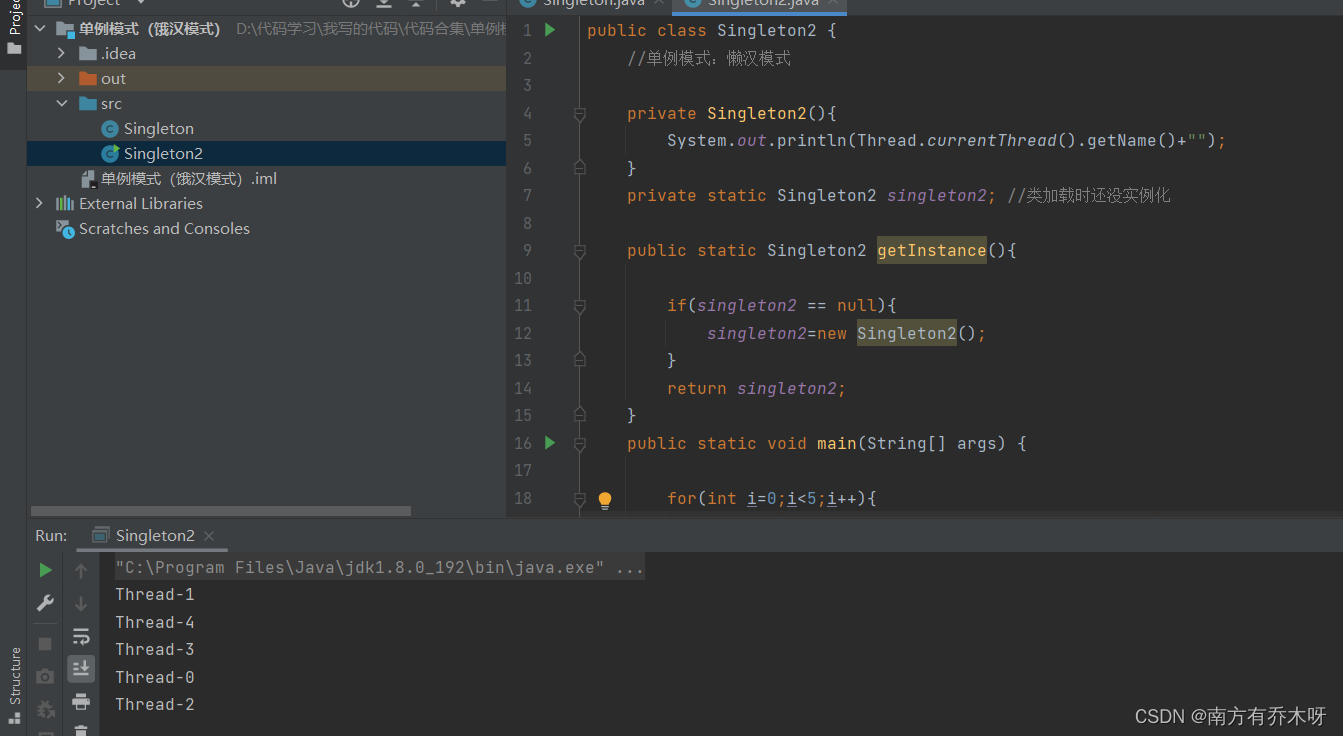
关于单例模式

单例模式的目的&#xff1a; 单例模式的目的和其他的设计模式的目的都是一样的&#xff0c;都是为了降低对象之间的耦合性&#xff0c;增加代码的可复用性&#xff0c;可维护性和可扩展性。 单例模式&#xff1a; 单例模式是一种常用的设计模式&#xff0c;用简单的言语说&am…...

编程日记 2023/8/29 18:59:52

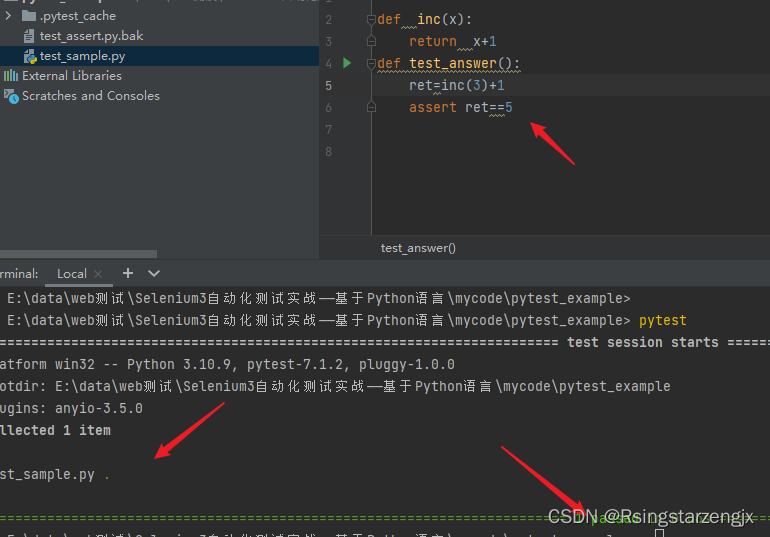
pytest笔记： pytest单元测试框架

第一步&#xff1a;安装 和查看版本 pycharm settings 查看 第二步&#xff1a; 编写test_example.py def inc(x):return x1 def test_answer():assert inc(4) 5 第三步&#xff1a;在当前路径下执行pytest 命令 PS E:\data\web测试\Selenium3自动化测试实战——基于Pyth…...

编程日记 2023/8/29 18:58:50

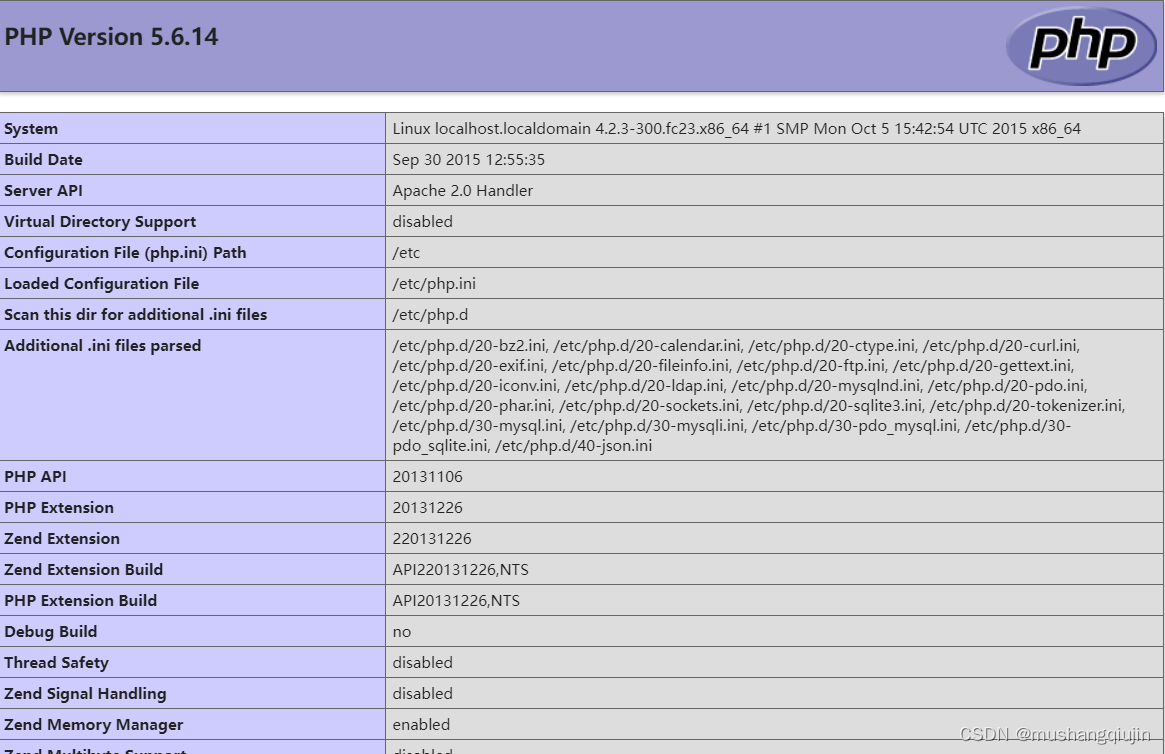
vulnhub Seattle-0.0.3

环境&#xff1a;vuluhub Seattle-0.0.3 1.catelogue处任意文件下载(目录穿越) http://192.168.85.139/download.php?item../../../../../../etc/passwd 有个admin目录&#xff0c;可以下载里面的文件进行读取 2.cltohes详情页面处(参数prod)存在sql报错注入 http://192.16…...

编程日记 2023/8/29 18:57:49

MYSQL 添加行号将行号写入到主键的列

MYSQL 添加行号 SELECT rownum: rownum 1 AS rownum, a.* FROM(SELECT rownum : 0) t,is_afxt.hk_vehicle a--或者(假设CREATED_TIME日期列数据不重复) select (select count(1)1 from is_afxt.hk_vehicle b where b.CREATED_TIME < a.CREATED_TIME) rownum ,a.* from i…...

编程日记 2023/8/29 18:56:48

前端命令npm 、 cnpm、 pnpm、yarn 、 npx、nvm的区别

大名鼎鼎的npm(Node Package Manager)是随同NodeJS一起安装的包管理工具&#xff0c;NPM本身也是Node.js的一个模块。 npm的含义有两层: npm服务器&#xff0c;npm服务器网址为https://www.npmjs.org&#xff0c;npm是 Node 包的标准发布平台&#xff0c;用于 Node 包的发布、…...

编程日记 2023/8/29 18:55:45

Linux 发行版 Debian 宣布支持龙芯 LoongArch 架构

近期&#xff0c;龙芯发布了 3A6000 桌面处理器&#xff0c;芯片的性能又一次大幅度提升&#xff0c;成为国产芯片的又一里程碑。 同期&#xff0c;LoongArch 架构的生态建设也迅速提升&#xff0c;开源网络引导固件 iPXE、QQ Linux 版、摩尔线程等软硬件都官宣支持龙芯 Loong…...

编程日记 2023/8/29 18:54:44

Reset Windows Update Tool：开源工具解决Windows更新问题的3个高效方案

Reset Windows Update Tool&#xff1a;开源工具解决Windows更新问题的3个高效方案 【免费下载链接】Reset-Windows-Update-Tool Troubleshooting Tool with Windows Updates (Developed in Dev-C). 项目地址: https://gitcode.com/gh_mirrors/re/Reset-Windows-Update-Tool …...

编程新知 2026/3/30 18:14:39

如何使用usearch进行水资源分配优化：用水数据的向量分析完整指南

如何使用usearch进行水资源分配优化&#xff1a;用水数据的向量分析完整指南 【免费下载链接】usearch Fastest Open-Source Search & Clustering engine for Vectors & &#x1f51c; Strings in C, C, Python, JavaScript, Rust, Java, Objective-C, Swift, C#, Go…...

编程新知 2026/3/30 18:10:37

大学物理（上）-期末实战解析（5）——刚体力学核心：从转动惯量到角动量守恒的解题秘籍

1. 刚体力学入门&#xff1a;为什么转动惯量是解题钥匙 刚体力学是大学物理中最让人头疼的章节之一&#xff0c;尤其是当题目里出现"转动惯量"这个名词时&#xff0c;很多同学就开始手心冒汗。记得我第一次做这类题目时&#xff0c;盯着那个积分符号看了半小时愣是没…...

编程新知 2026/3/30 17:50:17

HTTP自动化测试架构：基于QD框架的HAR模板规模化治理策略

HTTP自动化测试架构&#xff1a;基于QD框架的HAR模板规模化治理策略 【免费下载链接】templates 基于开源新版 QD 框架站发布的公共har模板库&#xff0c;仅供示例 项目地址: https://gitcode.com/GitHub_Trending/templa/templates 在当今云原生和微服务架构盛行的时代…...

编程新知 2026/3/30 16:35:23

汇编开发与系统构建：FloppyBird操作系统游戏的技术解构

汇编开发与系统构建&#xff1a;FloppyBird操作系统游戏的技术解构 【免费下载链接】floppybird Floppy Bird (OS) 项目地址: https://gitcode.com/gh_mirrors/fl/floppybird 一、价值&#xff1a;当游戏成为操作系统的技术突破 在计算机科学领域&#xff0c;"操作…...

编程新知 2026/3/30 16:15:11

RAGFlow图片回答避坑指南：为什么不用Base64和阿里云OSS？

RAGFlow图片回答架构设计&#xff1a;从Base64到容器化服务器的技术演进 当RAG系统需要处理包含图片的回答时&#xff0c;技术选型直接关系到系统的性能、安全性和可维护性。本文将深入探讨几种主流方案的优劣对比&#xff0c;并解析为何容器化图片服务器成为当前最优解。 1. 图…...

编程新知 2026/3/30 14:50:33

TripoSR：0.5秒单图像3D重建技术指南与实战应用

TripoSR&#xff1a;0.5秒单图像3D重建技术指南与实战应用 【免费下载链接】TripoSR 项目地址: https://gitcode.com/GitHub_Trending/tr/TripoSR 在3D内容创作领域&#xff0c;传统建模流程耗时耗力&#xff0c;而TripoSR作为开源3D重建模型&#xff0c;通过单张2D图像…...

编程新知 2026/3/30 14:48:25

[双重嵌入架构]：实现高精度人脸生成的AI解决方案

[双重嵌入架构]&#xff1a;实现高精度人脸生成的AI解决方案 【免费下载链接】IP-Adapter-FaceID 项目地址: https://ai.gitcode.com/hf_mirrors/h94/IP-Adapter-FaceID 1. 技术原理&#xff1a;双重嵌入架构的创新突破 1.1 并行特征处理机制 IP-Adapter-FaceID Plus…...

编程新知 2026/3/30 14:24:05

手把手教你配置：用微型纵向加密搞定IEC-104协议的风光数据安全上传

新能源场站IEC-104协议安全传输实战&#xff1a;微型纵向加密配置全指南 在新能源场站的自动化系统中&#xff0c;IEC-104协议作为电力行业标准通信规约&#xff0c;承担着风机、光伏逆变器与升压站之间关键运行数据传输的重任。然而&#xff0c;传统光纤环网中的明文传输方式存…...

编程新知 2026/3/30 13:00:24

【OFDM通信】基于matlab室内NOMA-OFDM-VLC系统仿真【含Matlab源码 15240期】

&#x1f4a5;&#x1f4a5;&#x1f4a5;&#x1f4a5;&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;&#x1f49e;&#x1f49e;&#x1f49e;&#x1f49e;&#x1f49e;&#x1f49e;欢迎来到海神之光博客之家&#x1f49e;&#x1f49e;&#x1f49e;&#x1f49…...

编程新知 2026/3/30 12:44:18