暴力递归转动态规划(二)
上一篇已经简单的介绍了暴力递归如何转动态规划,如果在暴力递归的过程中发现子过程中有重复解的情况,则证明这个暴力递归可以转化成动态规划。
这篇帖子会继续暴力递归转化动态规划的练习,这道题有点难度。
题目
给定一个整型数组arr[],代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌。规定玩家A先拿,玩家B后拿,但是每个玩家每次只能拿走最左边或者最右边的牌,玩家A和玩家B都绝顶聪明,请返回最后获胜者的分数。
暴力递归
依然是先从暴力递归开始写起,一个先手拿,一个后手拿,两个人都绝顶聪明,都知道怎么拿可以利益最大化。
先手的拿完第一个之后,再拿的时候,就要从后手拿完的数组里再挑选了。
同理,如果后手的等先手的拿了之后,是不是就可以从剩余的数组里挑选最大利益的拿了。
依然先确定base case:
如果先手拿,最理想的状态就是当数组剩下最后一个数,依然可以被我拿走。
如果后手拿,最悲催的连数组最后一个数我都拿不到。
代码中f()函数是代表在数组L~ R范围上返回上先手拿能拿到的最大值返回。
g()函数代表在数组L ~ R范围上后手拿,能够获取的最大值。
需要注意的是身份的转变,如果先手拿之后,再拿的时候就会变成后手,第二个后手拿的时候,虽然我是后手,但是也是从数组中挑选利益最大的拿,留给先手拿的人的也是不好的,所以我会变成先手。
//先手方法
public static int f(int[] arr,int L,int R){//base case:先手拿,并且数组中剩一个元素,我拿走if(L == R){return arr[L];}//因为可以选择从左边拿和右边拿,从左边拿下一次就是L + 1开始,右边拿就是 R - 1 开始。//需要注意的是我从左或者从右拿完之后,再拿就是拿别人拿剩下的了,要以后手姿态获取其余分数,所以要调用g()方法int p1 = arr[L] + g(arr,L + 1,R);int p2 = arr[R] + g(arr, L, R -1);//两种决策中取最大值return Math.max(p1,p2);
}
//后手方法
public static int g(int[] arr,int L,int R){//剩最后一个也不是我的,毛都拿不到,return 0if(L == R){return 0;}//后手方法是在先手方法后,挑选最大值,那如果先手方法选择了L,则我要从L + 1位置选,//如果先手选择了R,那我要从R - 1位置开始往下选。//是从对手选择后再次选择最大值int p1 = f(arr,L + 1,R);int p2 = f(arr,L,R - 1);//因为是后手,是在先手后做决定,是被迫的,所以取Min。return Math.min(p1,p2);
}
先手后手方法已经确定,来看主流程怎么调用
public static int win1(int[] arr){//如果是无效数组,则返回一个无效数字 -1 if(arr == null || arr.length == 0){return -1;}int first = f(arr, 0 ,arr.length - 1);int second = g(arr,0,arr.length - 1);return Math.max(first,second);
}
暴力递归的分析和代码已经搞定,接下来我们通过分析暴力递归的调用过程来实现第一步的优化,找它的依赖,找它的重复解。
举一个具体的例子,arr[]范围 0~ 7,根据上面暴力递归的代码逻辑,我们来看看它的依赖关系和调用过程。如果确定了可变参数以及依赖关系,是不是就可以尝试着优化成动态规划。
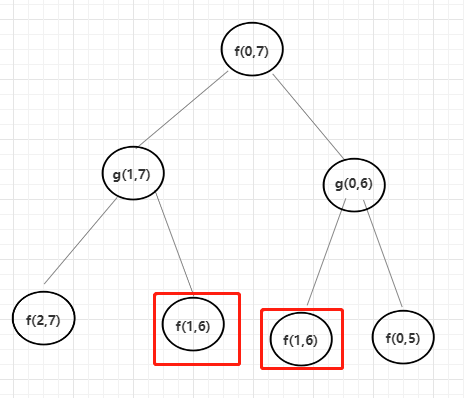
根据代码逻辑,要么是取左边L + 1,要么是取右边 R - 1,所以可以确定可变参数是L和R,并且整个流程下来会发现有重复解的情况。
不过有些不同的是,这个是双层递归循环依赖调用,所以如果根据可变参数参数L,R来构建缓存表的话,则需要2个不同的缓存表分别记录。
优化
前面已经分析出整个暴力递归的调用过程,并发现了重复解,其中可变参数是L、R,根据L、R构建缓存表,因为是f()和g()的循环依赖调用,所以需要准备两张缓存表。
public static int win2(int[] arr) {if (arr == null || arr.length == 0) {return -1;}int N = arr.length;int[][] fmap = new int[N][N];int[][] gmap = new int[N][N];for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {fmap[i][j] = -1;gmap[i][j] = -1;}}int first = f1(arr, 0, arr.length - 1, fmap, gmap);int second = g1(arr, 0, arr.length - 1, fmap, gmap);return Math.max(first, second);}public static int f1(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {// != -1,说明之前计算过该值,直接返回即可if (fmap[L][R] != -1) {return fmap[L][R];}int ans = 0;if (L == R){ans = arr[L];}else{int p1 = arr[L] + g1(arr, L + 1, R, fmap, gmap);int p2 = arr[R] + g1(arr, L, R - 1, fmap, gmap);ans = Math.max(p1, p2);}//这一步能够取得的最大值fmap[L][R] = ans;return ans;}public static int g1(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {if (gmap[L][R] != -1){return gmap[L][R];}//因为如果 L == R,后手方法会返回0,默认ans也是等于0,省略一步判断int ans = 0;if (L != R){int p1 = f1(arr,L + 1,R,fmap,gmap);int p2 = f1(arr,L,R - 1,fmap,gmap);ans = Math.min(p1,p2);}gmap[L][R] = ans;return ans;}
二次优化
我们上面已经创建了缓存表,并找到了变量L、R,我们现在不妨举一个例子,并将缓存表画出来,来看一下表中每一列的对应关系,如果我们能找到这个缓存表的对应关系,是不是将表构建出来以后,就可以直接获取获胜者的最大值。
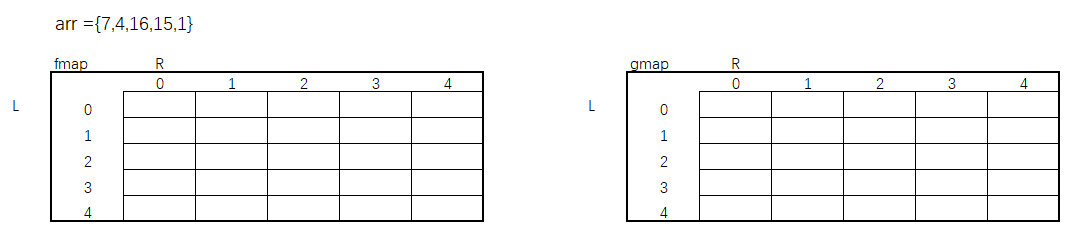
数组arr = {7,4,16,15,1} 因为有两张缓存表,所以需要将两张表的依赖关系都找出。接下来,回到最开始的暴力递归方法,根据代码逻辑一步一步找出依赖关系。
public static int win1(int[] arr) {if (arr == null || arr.length == 0) {return -1;}int first = f(arr, 0, arr.length - 1);int second = g(arr, 0, arr.length - 1);return Math.max(first, second);}public static int f(int[] arr, int L, int R) {if (L == R) {return arr[L];}int p1 = arr[L] + g(arr, L + 1, R);int p2 = arr[R] + g(arr, L, R - 1);return Math.max(p1, p2);}public static int g(int[] arr, int L, int R) {if (L == R) {return 0;}int p1 = f(arr, L + 1, R);int p2 = f(arr, L, R - 1);return Math.min(p1, p2);}
从先手方法f()和后手方法g()的base case可以看出,如果当L == R时,f()方法中此时就是等于数组arr[L]本身的值,而g()中为0,又因为,每次我只选L或只选R,当L = R时就return了,所以我的L始终不会 > R。我们所要求的L ~ R 范围是整个数组0 ~ 4的值,此时图可以填充成这样。
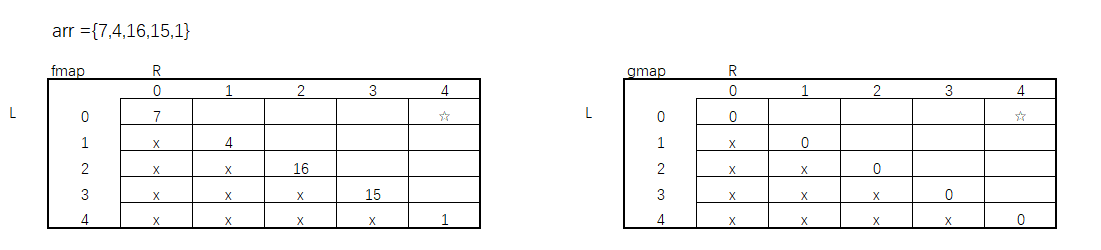
再来接着往下看,如果此时LR随便给一个值,比如说当前fmap中L = 1,R = 3,来接着看它的依赖过程。
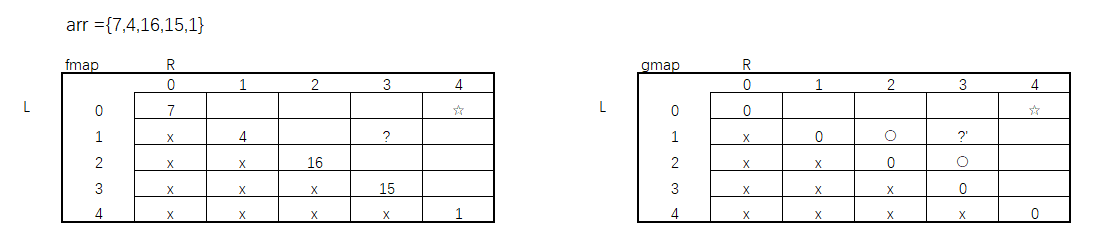
根据代码可以看出,它依赖的是g()方法中L +1和R - 1,所以对应在gmap中的依赖就是圆圈标记的部分。对应的,同样 L = 1 R = 3在gmap中也是依赖fmap对应的位置。
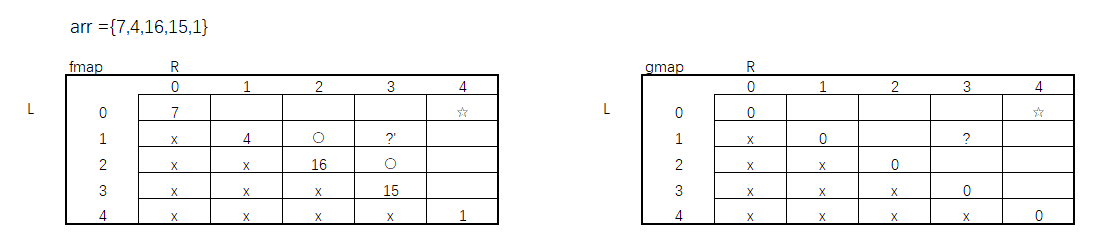
那现在有缓存表中每个位置的依赖关系,还有fmap和gmap当L == R时的值,是不是就可以推算出其他格子中的值。
代码
public static int win3(int[] arr) {if (arr == null || arr.length == 0) {return -1;}int N = arr.length;int[][] fmap = new int[N][N];int[][] gmap = new int[N][N];//根据base case填充fmap,gmap都是0,数组初始化值也是0,不用填充for (int i = 0; i < N; i++) {fmap[i][i] = arr[i];}//根据对角线填充,从第一列开始for (int startCol = 1; startCol < N; startCol++) {int L = 0;int R = startCol;while (R < N) {//将调用的g()和f()都替换成对应的缓存表fmap[L][R] = Math.max(arr[L] + gmap[L + 1][R], arr[R] + gmap[L][R - 1]);gmap[L][R] = Math.min(fmap[L + 1][R], fmap[L][R - 1]);L++;R++;}}//最后从L ~ R位置,取最大值return Math.max(fmap[0][N -1],gmap[0][N-1]);}
相关文章:

暴力递归转动态规划(二)
上一篇已经简单的介绍了暴力递归如何转动态规划,如果在暴力递归的过程中发现子过程中有重复解的情况,则证明这个暴力递归可以转化成动态规划。 这篇帖子会继续暴力递归转化动态规划的练习,这道题有点难度。 题目 给定一个整型数组arr[]&…...

debian apt error: Package ‘xxx‘ has no installation candidate
新的debian虚拟机可能会出现这个问题。 修改apt的source.list,位于/etc/apt/source.list,添加两行: deb http://deb.debian.org/debian bullseye main deb-src http://deb.debian.org/debian bullseye main执行: sudo apt-get u…...
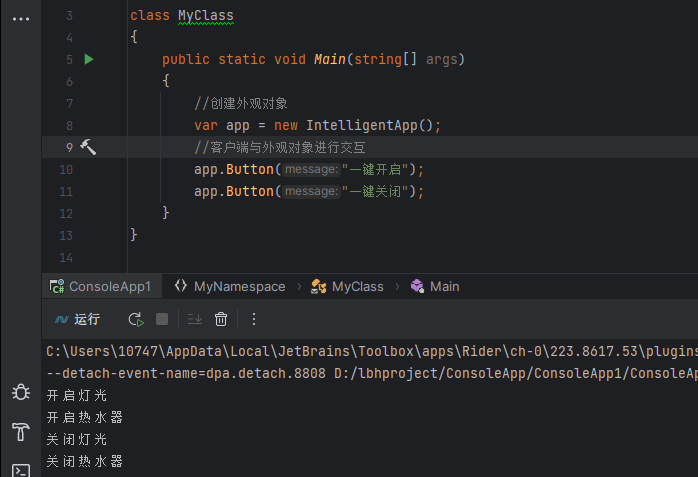
c#设计模式-结构型模式 之 外观模式
概述 外观模式(Facade Pattern)又名门面模式,隐藏系统的复杂性,并向客户端提供了一个客户端可以访问系统的接口。这种类型的设计模式属于结构型模式,它向现有的系统添加一个接口,来隐藏系统的复杂性。该模式…...

Focal Loss-解决样本标签分布不平衡问题
文章目录 背景交叉熵损失函数平衡交叉熵函数 Focal Loss损失函数Focal Loss vs Balanced Cross EntropyWhy does Focal Loss work? 针对VidHOI数据集Reference 背景 Focal Loss由何凯明提出,最初用于图像领域解决数据不平衡造成的模型性能问题。 交叉熵损失函数 …...

运算符(个人学习笔记黑马学习)
算数运算符 加减乘除 #include <iostream> using namespace std;int main() {int a1 10;int a2 20;cout << a1 a2 << endl;cout << a1 - a2 << endl;cout << a1 * a2 << endl;cout << a1 / a2 << endl;/*double a3 …...

开源与专有软件:比较与对比
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

openResty+lua+redis实现接口访问频率限制
openResty简介: OpenResty 是一个基于 Nginx 与 Lua 的高性能 Web 平台,其内部集成了大量精良的 Lua 库、第三方模块以及大多数的依赖项。用于方便地搭建能够处理超高并发、扩展性极高的动态 Web 应用、Web 服务和动态网关。 OpenResty 通过汇聚各种设…...
自动化测试(三):接口自动化pytest测试框架
文章目录 1. 接口自动化的实现2. 知识要点及实践2.1 requests.post传递的参数本质2.2 pytest单元测试框架2.2.1 pytest框架简介2.2.2 pytest装饰器2.2.3 断言、allure测试报告2.2.4 接口关联、封装改进YAML动态传参(热加载) 2.3 pytest接口封装ÿ…...

Python --datetime模块
目录 1, 获取datetime时间 2, datetime与timestamp转换 2-1, datetime转timestamp 2-2, timestamp转datetime 3, str格式与datetime转换 3-1, datetime转str格式 3-2, str格式转datetime…...
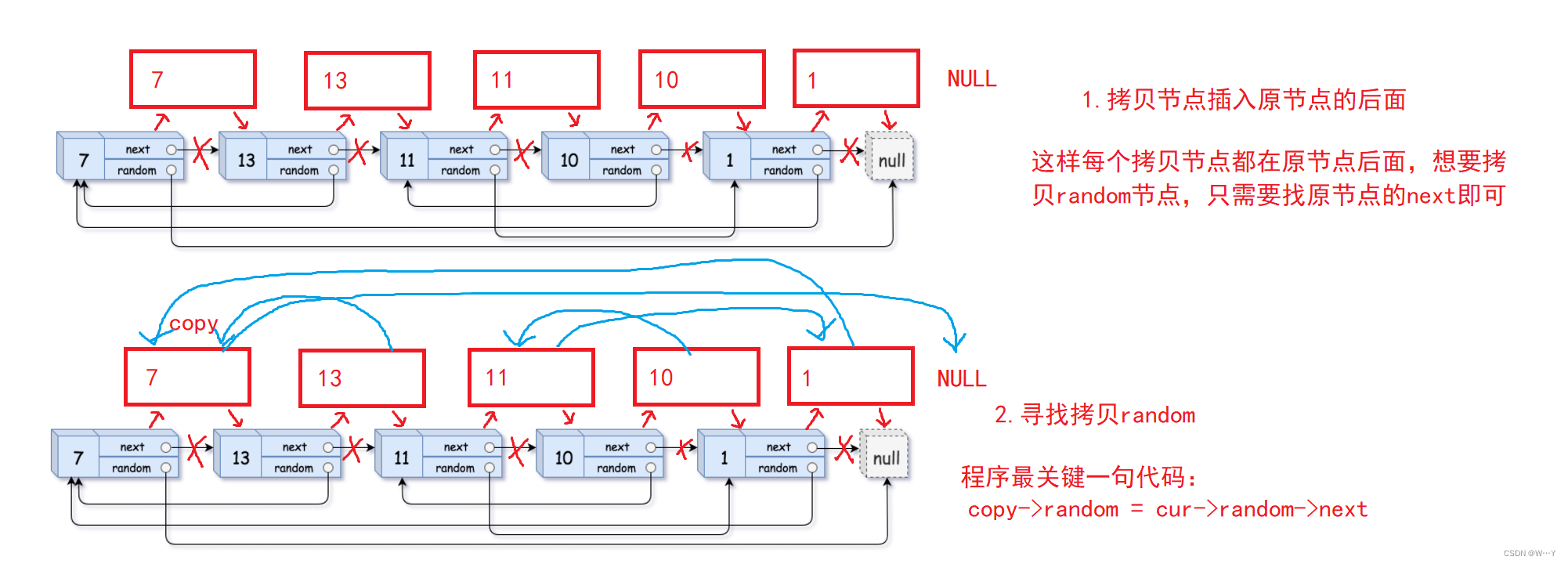
顺序表链表OJ题(3)——【数据结构】
W...Y的主页 😊 代码仓库分享 💕 前言: 今天是链表顺序表OJ练习题最后一次分享,每一次的分享题目的难度也再有所提高,但是我相信大家都是非常机智的,希望看到博主文章能学到东西的可以一键三连关注一下博主…...

【Azure】Virtual Hub vWAN
虚拟 WAN 文档 Azure 虚拟 WAN 是一个网络服务,其中整合了多种网络、安全和路由功能,提供单一操作界面。 我们主要讨论两种连接情况: 通过一个 vWAN 来连接不通的 vNET 和本地网络。以下是一个扩展的拓扑 结合 vhub,可以把两个中…...

React Navigation 使用导航
在 Web 浏览器中,您可以使用锚标记链接到不同的页面。当用户单击链接时,URL 会被推送到浏览器历史记录堆栈中。当用户按下后退按钮时,浏览器会从历史堆栈顶部弹出该项目,因此活动页面现在是以前访问过的页面。React Native 不像 W…...
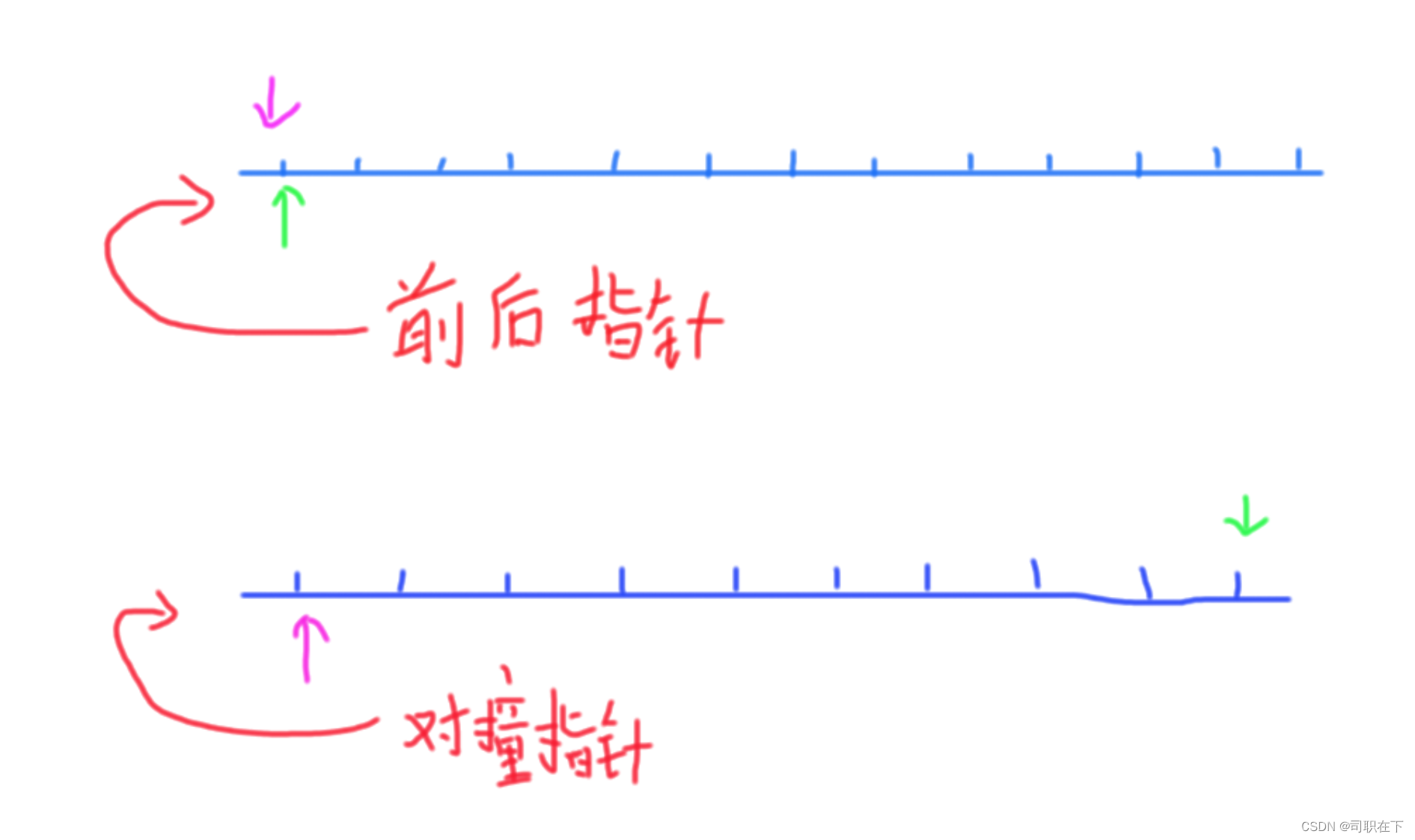
双指针算法,基础算法实践,基本的算法的思想,双指针算法的实现
一,定义 双指针算法是一种常用于解决数组和链表问题的算法技巧。它的核心思想是使用两个指针在数据结构中按照一定的规则移动,从而达到快速搜索或处理数据的目的。这个技巧通常用于优化算法,降低时间复杂度,提高程序的执行效率。…...
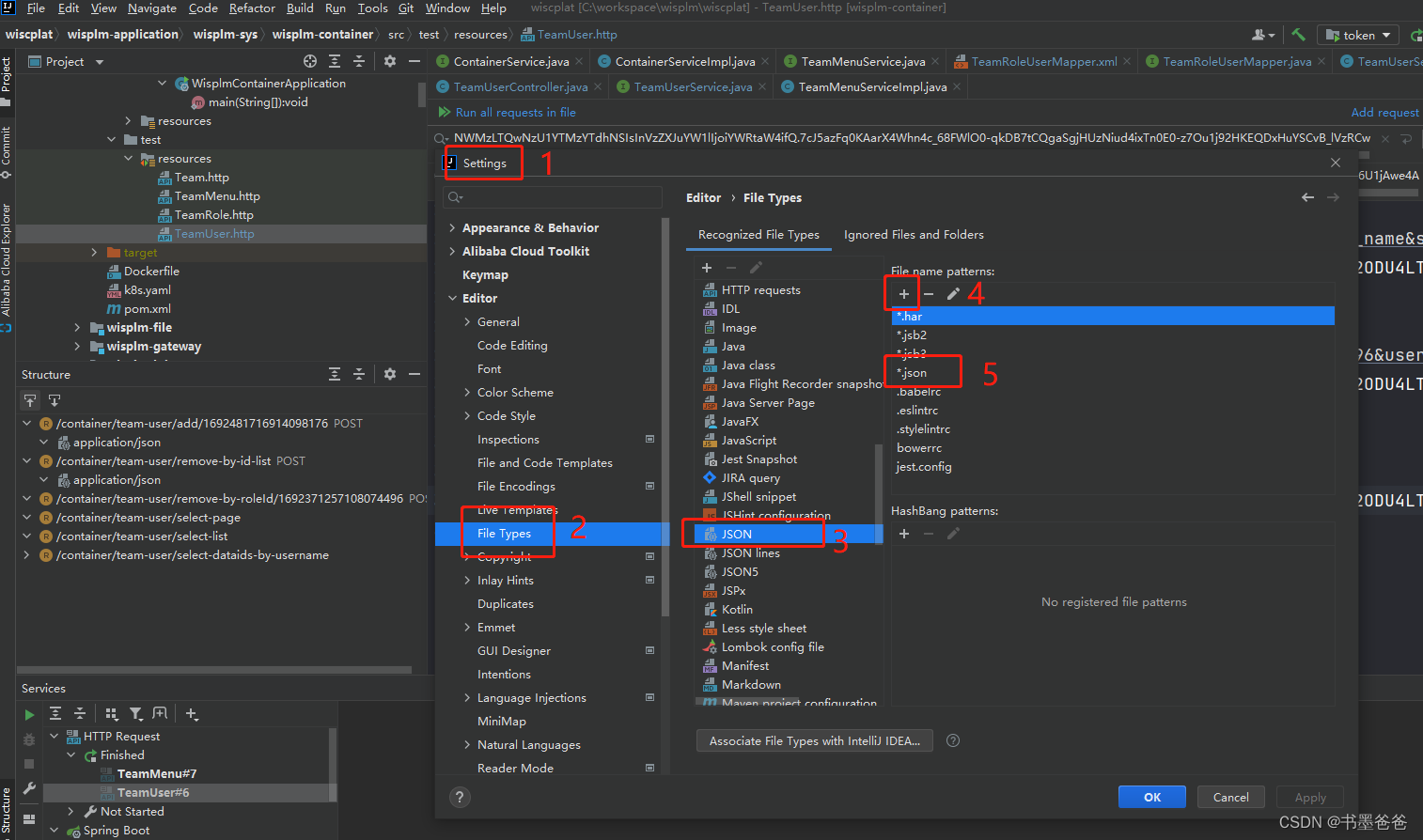
idea http request无法识别环境变量
问题描述 创建了环境变量文件 http-client.env.json,然后在*.http 文件中引用环境变量,运行 HTTP 请求无法读取环境变量文件中定义的变量。 事故现场 IDEA 版本:2020.2 2021.2 解决步骤 2020.2 版本环境变量无法读取 2021.2 版本从 2020.…...

性能测试常见的测试指标
一、什么是性能测试 先看下百度百科对它的定义 性能测试是通过自动化的测试工具模拟多种正常、峰值以及异常负载条件来对系统的各项性能指标进行测试。我们可以认为性能测试是:通过在测试环境下对系统或构件的性能进行探测,用以验证在生产环境下系统性能…...
并发 04(Callable,CountDownLatch)详细讲解
并发 Callable 1 可以返回值 2可以抛出异常 泛型指的是返回值的类型 public class Send {public static void main(String[] args) {//怎么启动Callable//new Thread().start();Aaa threadnew Aaa();FutureTask futureTasknew FutureTask(thread);new Thread(futureTask,&qu…...

Json路径表达式
原json路径 {"timeStamp": "20220801110008","transIDO": "6ba9088c981b407fb38feasdf09","version": "1.0.0","signMethod": "md5","content": "{\"companyName\&quo…...

【uniapp 上传图片示例】
以下是 uniapp 上传图片的详细步骤示例: 定义一个方法,用于选择图片并上传: methods: {chooseImage() {uni.chooseImage({count: 1, // 最多选择的图片数量sizeType: [original, compressed], // 可以指定原图或压缩图sourceType: [album, …...

apache2配置文件 Require all granted是什么意思
修改apache2的配置文件 /etc/apache2/apache2.conf,需要增加网站代码的路径,下列配置是什么意思呢 <Directory "/var/www/html">Options FollowSymLinksAllowOverride AllRequire all granted </Directory> 1. Options Options …...

c/c++ 的一些知识
c 面向对象是一种思想,通常情况下都是以组合为主,也就是在子类里定义一个基类struct base_t {void (*method)(base_t *base_p); };struct children_t {int a;int b;base_t base;void (*method)(children_t *children_p); };children_t children_creat(i…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
