【算法】经典的八大排序算法
点击链接 可视化排序 动态演示各个排序算法来加深理解,大致如下
一,冒泡排序(Bubble Sort)
原理
- 冒泡排序(Bubble Sort)是一种简单的排序算法,它通过多次比较和交换相邻元素的方式,将最大(或最小)的元素逐步冒泡到数组的一端。每一轮冒泡将会将未排序部分中最大(或最小)的元素“浮”到正确的位置。
算法步骤
- 从数组的第一个元素开始,依次比较相邻的两个元素。
- 如果前一个元素比后一个元素大(或小,取决于排序顺序),则交换这两个元素。
- 继续向后遍历,对每一对相邻元素重复步骤 2。
- 重复步骤 1 到 3,直到没有元素需要交换,整个数组就是有序的。
算法实现
#include <iostream> #include <vector>// 冒泡排序 void bubbleSort(std::vector<int>& arr) {int n = arr.size();for (int i = 0; i < n - 1; ++i) {// 在每一轮中,比较相邻元素并交换for (int j = 0; j < n - i - 1; ++j) {if (arr[j] > arr[j + 1]) {std::swap(arr[j], arr[j + 1]);}}} }性能分析
- 时间复杂度:
- 冒泡排序的时间复杂度在最坏和平均情况下都为 O(n^2),其中 n 是待排序元素的数量。每次遍历需要进行 n-1 次比较,而需要执行 n-1 次遍历。
- 最好情况下,如果列表本身已经有序,冒泡排序仍然需要进行 n-1 次遍历,但由于没有发生交换,每次遍历只需要进行 n-1、n-2、...、2、1 次比较,时间复杂度为 O(n)。
- 空间复杂度:
- 冒泡排序的空间复杂度为 O(1),只需要常数级别的额外空间。
- 稳定性:
- 冒泡排序是稳定的排序算法,因为它在相邻元素比较时仅在必要时才进行交换。
二,选择排序(Selection Sort)
原理
- 选择排序(Selection Sort)是一种简单的排序算法,它将待排序数组分为已排序和未排序两部分,然后从未排序部分选择最小(或最大)的元素,与已排序部分的最后一个元素交换位置。每次交换都会将一个元素归位,直到整个数组有序。
算法步骤
- 初始时,将整个序列分为已排序和未排序两部分,已排序为空,未排序包含所有元素。
- 在未排序部分中,找到最小(或最大)的元素。
- 将找到的最小元素与未排序部分的第一个元素交换位置,将其放到已排序部分的末尾。
- 重复执行步骤 2 和 3,直到未排序部分为空,整个序列变得有序。
算法实现
#include <iostream> #include <vector>// 选择排序 void selectionSort(std::vector<int>& arr) {int n = arr.size();for (int i = 0; i < n - 1; ++i) {int minIndex = i; // 记录最小元素的索引// 在未排序部分找到最小元素的索引for (int j = i + 1; j < n; ++j) {if (arr[j] < arr[minIndex]) {minIndex = j;}}// 将最小元素与当前位置交换std::swap(arr[i], arr[minIndex]);} }性能分析
- 时间复杂度:
- 选择排序的时间复杂度在最好、最坏和平均情况下都是 O(n^2),其中 n 是待排序元素的数量。
- 空间复杂度:
- 选择排序的空间复杂度为 O(1),只需要常数级别的额外空间。
- 稳定性:
- 选择排序是不稳定的排序算法,因为在选择最小(或最大)元素的过程中,相同值的元素可能会交换位置。
三,插入排序(Insertion Sort)
原理
- 插入排序(Insertion Sort)是一种简单的排序算法,它将待排序数组分为已排序和未排序两部分,然后逐个将未排序部分的元素插入到已排序部分的正确位置,使得已排序部分始终保持有序。
算法步骤
- 初始时,将第一个元素视为已排序部分,其余元素视为未排序部分。
- 从未排序部分中取出一个元素,将其插入到已排序部分的适当位置,使得插入后的已排序部分仍然保持有序。
- 重复步骤 2,直到未排序部分为空,整个序列变得有序。
算法实现
#include <iostream> #include <vector>// 插入排序 void insertionSort(std::vector<int>& arr) {int n = arr.size();for (int i = 1; i < n; ++i) {int current = arr[i]; // 当前要插入的元素int j = i - 1; // 已排序部分的末尾索引// 将元素插入到正确位置while (j >= 0 && arr[j] > current) {arr[j + 1] = arr[j];j--;}arr[j + 1] = current;} }性能分析
- 时间复杂度:
- 插入排序的时间复杂度在最好情况下是 O(n),最坏和平均情况下是 O(n^2),其中 n 是待排序元素的数量。
- 空间复杂度:
- 插入排序的空间复杂度为 O(1),只需要常数级别的额外空间。
- 稳定性:
- 插入排序是稳定的排序算法,因为它在插入元素时相同值的元素不会改变相对顺序。
四,希尔排序(Shell Sort)
原理
- 希尔排序(Shell Sort)是一种改进的插入排序算法,它通过将数组分成多个子序列来排序,然后逐步缩小子序列的间隔,最终将整个数组排序。希尔排序的核心思想是使数组中任意间隔 h 的元素都是有序的,当 h 逐步减小到 1 时,整个数组变为有序。
算法步骤
- 选择一个增量序列(通常为递减的整数序列),例如 [n/2, n/4, n/8, ...],其中 n 是数组的长度。
- 对每个增量进行迭代,将数组分成多个子数组,每个子数组中的元素间隔为增量。
- 对每个子数组进行插入排序,将子数组中的元素插入到已排序部分的适当位置。
- 重复步骤 2 和 3,不断减小增量,直到增量为 1,此时整个数组被视为一个子数组,进行最后一次插入排序。
算法实现
#include <iostream>void shellSort(int arr[], int n) {for (int gap = n / 2; gap > 0; gap /= 2) {// 使用插入排序对子数组进行排序for (int i = gap; i < n; ++i) {int temp = arr[i];int j = i;// 移动元素,寻找插入位置while (j >= gap && arr[j - gap] > temp) {arr[j] = arr[j - gap];j -= gap;}arr[j] = temp; // 将元素插入到合适的位置}} }性能分析
- 时间复杂度:
- 希尔排序的时间复杂度依赖于所选的增量序列。最好的已知增量序列的时间复杂度是 O(n^1.3),平均情况下的时间复杂度较难分析,但它通常优于 O(n^2) (介于 O(n log n) 和 O(n^2) 之间)的插入排序。具体取决于增量序列的选择。
- 空间复杂度:
- 希尔排序的空间复杂度为 O(1),只需要常数级别的额外空间。
- 稳定性:
- 希尔排序不是稳定的排序算法,因为在交换元素的过程中可能会改变相同值元素的相对顺序。
五,归并排序(Merge Sort)
原理
- 归并排序(Merge Sort)是一种分治策略的排序算法,它将待排序数组不断划分为两个子数组,然后将这些子数组逐步合并成一个有序数组。归并排序的核心思想是将两个有序的子数组合并成一个有序的数组,这样逐步合并,最终得到整个数组有序。
算法步骤
- 分割:将待排序数组递归地分割成较小的子数组,直到每个子数组只包含一个元素。
- 合并:将两个有序的子数组合并成一个有序数组。合并过程中,分别从两个子数组中取出较小的元素,放入结果数组中。
算法实现
#include <iostream> #include <vector>// 合并两个有序子数组 void merge(std::vector<int>& arr, int left, int mid, int right) {int leftCount = mid - left + 1; // 左边子数组大小int rightCount = right - mid; // 右边子数组大小// 创建临时数组存放两个子数组的元素std::vector<int> leftArr(leftCount), rightArr(rightCount);for (int i = 0; i < leftCount; ++i)leftArr[i] = arr[left + i];for (int i = 0; i < rightCount; ++i)rightArr[i] = arr[mid + 1 + i];// 合并两个子数组int i = 0, j = 0, k = left;while (i < leftCount && j < rightCount) {if (leftArr[i] <= rightArr[j]) {arr[k++] = leftArr[i++];} else {arr[k++] = rightArr[j++];}}// 将剩余的元素拷贝到结果数组中while (i < leftCount) {arr[k++] = leftArr[i++];}while (j < rightCount) {arr[k++] = rightArr[j++];} }// 归并排序 void mergeSort(std::vector<int>& arr, int left, int right) {if (left < right) {int mid = left + (right - left) / 2;// 递归地对左右子数组进行排序mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);// 合并两个有序子数组merge(arr, left, mid, right);} }性能分析
- 时间复杂度:
- 归并排序的时间复杂度是稳定的,无论数据的分布如何,都是 O(n log n),其中 n 是待排序元素的数量。
- 空间复杂度:
- 归并排序需要额外的空间来存储临时数组,因此其空间复杂度是 O(n)。
- 稳定性:
- 归并排序是稳定的排序算法,因为在合并两个子数组时,相同值的元素不会改变相对顺序。
六,快速排序(Quick Sort)
原理
- 快速排序(Quick Sort)是一种基于分治思想的排序算法,它通过选择一个基准元素,将数组划分为小于基准和大于基准的两部分,然后递归地对这两部分进行排序。在每一次划分后,基准元素会被放置在最终的正确位置上。
算法步骤
- 选择基准元素:从数组中选择一个基准元素,通常选择第一个或最后一个元素。
- 分区:将数组划分为小于基准和大于基准的两部分,使得基准元素位于正确的位置上。
- 递归排序:对小于基准和大于基准的两部分分别递归地应用快速排序算法。
- 合并:不需要合并步骤,因为在分区过程中已经将数组划分为有序的部分。
算法实现
#include <iostream> #include <vector>// 分区函数,返回基准元素的正确位置 int partition(std::vector<int>& arr, int low, int high) {int pivot = arr[low]; // 选择第一个元素作为基准while (low < high){while (low<high && arr[high]>=pivot)--high;arr[low] = arr[high]; // 将小于基准的元素移到左边while (low<high && arr[low]<=pivot)++low;arr[high] = arr[low]; // 将大于基准的元素移到右边}// 将基准元素放到正确的位置上arr[low] = pivot;return low; // 返回存放基准的最终位置 }// 快速排序 void quickSort(std::vector<int>& arr, int low, int high) {if (low < high) {int pivotIndex = partition(arr, low, high); // 基准元素的正确位置// 对基准左边和右边的部分分别递归进行排序quickSort(arr, low, pivotIndex - 1);quickSort(arr, pivotIndex + 1, high);} }性能分析
- 时间复杂度:
- 平均情况下,快速排序的时间复杂度是 O(n log n),其中 n 是待排序元素的数量。
- 在最坏情况下(数组已经有序或接近有序),快速排序的时间复杂度可能退化到 O(n^2)。
- 空间复杂度:
- 快速排序的空间复杂度主要取决于递归调用的栈空间,通常为 O(log n)。
- 在最坏情况下,递归栈的深度可能达到 n,空间复杂度为 O(n)。
- 稳定性:
- 快速排序是不稳定的排序算法,因为在分区过程中可能改变相同元素的相对顺序。
七,堆排序(Heap Sort)
原理
- 堆排序(Heap Sort)是一种基于二叉堆的排序算法。它将待排序数组构建成一个二叉堆,然后不断从堆顶取出最大(或最小)元素,将其放置到已排序部分的末尾,直到整个数组有序。
算法步骤
- 构建最大堆:将待排序数组看作完全二叉树,从最后一个非叶子节点开始,逐步向上调整,使得每个节点都大于其子节点。
- 不断从堆顶取出最大元素:每次将堆顶元素与堆末尾元素交换,然后将堆的大小减一,再进行堆化操作,将最大元素移至正确位置。
- 重复步骤 2,直到堆中只剩一个元素,此时整个数组有序。
算法实现
#include <iostream> #include <vector>// 交换元素 void swap(int& a, int& b) {a = a + b;b = a - b;a = a - b; }// 对以 root 为根的子树进行堆化 void heapify(std::vector<int>& arr, int n, int root) {int largest = root; // 初始化最大元素为根节点while (largest < n) {int left = 2 * root + 1; // 左子节点索引int right = 2 * root + 2; // 右子节点索引// 找到左右子节点中较大的元素索引if (left < n && arr[left] > arr[largest]) {largest = left;}if (right < n && arr[right] > arr[largest]) {largest = right;}// 如果最大元素不是根节点,则交换元素if (largest != root) {swap(arr[root], arr[largest]);root = largest; // 继续向下调整} else {break; // 堆结构已经满足,退出循环}} }// 堆排序 void heapSort(std::vector<int>& arr) {int n = arr.size();// 构建大根堆,从最后一个非叶子节点开始for (int i = n / 2 - 1; i >= 0; --i) {heapify(arr, n, i);}// 逐步取出最大元素并进行堆化for (int i = n - 1; i > 0; --i) {swap(arr[0], arr[i]); // 将堆顶元素移至已排序部分的末尾heapify(arr, i, 0); // 对剩余的部分进行堆化} }性能分析
- 时间复杂度:
- 堆排序的时间复杂度在最好、最坏和平均情况下都是 O(n log n),其中 n 是待排序元素的数量。
- 空间复杂度:
- 堆排序的空间复杂度为 O(1),只需要常数级别的额外空间。
- 稳定性:
- 堆排序通常是不稳定的,因为堆化操作可能改变相同元素的相对顺序。然而,通过一些额外的操作可以实现稳定性。
八,基数排序(Counting Sort)
原理
- 基数排序(Radix Sort)是一种非比较的整数排序算法,它根据数字的每个位上的值来对元素进行排序。基数排序可以看作是桶排序的扩展,它先按照最低位进行排序,然后逐步移到更高位,直到所有位都考虑完毕。
算法步骤
- 找到最大数的位数:首先,找到待排序数组中最大数的位数,这将决定排序的轮数。
- 按位排序:从低位到高位,依次对每一位进行计数排序(或桶排序),将元素分配到不同的桶中。
- 合并桶:将每一轮排序后的桶中的元素按顺序合并成一个新的数组。
- 重复步骤 2 和 3,直到所有位都考虑完毕,得到有序数组。
算法实现
#include <iostream> #include <vector> #include <queue>// 找到数组中的最大数 int findMax(std::vector<int>& arr) {int max = arr[0];for (int num : arr) {if (num > max) {max = num;}}return max; }// 基数排序 void radixSort(std::vector<int>& arr) {int n = arr.size();int max = findMax(arr);int exp = 1; // 用于获取每个位数的值while (max / exp > 0) {// 创建桶队列,每个桶用于存放某个位数上的元素std::vector<std::queue<int>> buckets(10); // 使用10个桶,每个桶代表一个数字(0到9)// 将元素分配到桶中for (int i = 0; i < n; ++i) {int bucketIndex = (arr[i] / exp) % 10; // 计算当前位数的值,作为桶的索引buckets[bucketIndex].push(arr[i]); // 将元素放入对应的桶中}// 从桶中取回元素到原数组int index = 0;for (int i = 0; i < 10; ++i) {while (!buckets[i].empty()) {arr[index++] = buckets[i].front(); // 取出队列头部元素,放入原数组buckets[i].pop(); // 弹出队列头部元素}}exp *= 10; // 移到下一个位数} }性能分析
- 时间复杂度:
- 基数排序的时间复杂度取决于位数和基数的大小。对于位数为 k,基数为 r 的情况,时间复杂度为 O(k * (n + r))。
- 空间复杂度:
- 基数排序的空间复杂度为 O(n + r),其中 n 是待排序元素的数量,r 是基数的大小。
- 稳定性:
- 基数排序是稳定的排序算法,因为在同一位数上的排序时,相同值元素的相对顺序不会改变。
相关文章:
【算法】经典的八大排序算法
点击链接 可视化排序 动态演示各个排序算法来加深理解,大致如下 一,冒泡排序(Bubble Sort) 原理 冒泡排序(Bubble Sort)是一种简单的排序算法,它通过多次比较和交换相邻元素的方式,将…...

防溺水预警识别系统算法
防溺水预警识别系统旨在通过opencvpython网络模型深度学习算法,防溺水预警识别系统算法实时监测河道环境,对学生等违规下水游泳等危险行为进行预警和提醒。Python是一种由Guido van Rossum开发的通用编程语言,它很快就变得非常流行࿰…...

Redis 的整合 Jedis 使用
大家好 , 我是苏麟 , 今天带来 Jedis 的使用 . Jedis的官网地址: GitHub - redis/jedis: Redis Java client 引入依赖 <!--jedis--> <dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId><version…...
Mainline Linux 和 U-Boot编译
By Toradex胡珊逢 Toradex 自从 Linux BSP v6 开始在使用 32位处理器的 Arm 模块如 iMX6、iMX6ULL、iMX7 上提供 mainline/upstream kernel ,部分 64位处理器模块如 Verdin iMX8M Mini/Plus 也提供实验性支持。文章将以季度发布版本 Linux BSP V6.3.0 为例介绍如何下…...
Mycat教程+面试+linux搭建
目录 一 MyCAT介绍 二 常见的面试题总结 三 linux下搭建Mycat 一 MyCAT介绍 1.1. 什么是MyCAT? 简单的说,MyCAT就是: 一个彻底开源的,面向企业应用开发的“大数据库集群” 支持事务、ACID、可以替代Mysql的加强版数据库 一个可…...

基于工作过程的高职计算机网络技术专业课程体系构建策略
行业人才需求分析高职教育是面向地方行业培养技能型、应用型人才,因此, 在课程体系的构建上要走社会调研、构建岗位群、构建专业模块及课程设置“四步 曲”。即通过社会行业需求调查研究,构建岗位群,设置相应的专业模块…...
(笔记四)利用opencv识别标记视频中的目标
预操作: 通过cv2将视频的某一帧图片转为HSV模式,并通过鼠标获取对应区域目标的HSV值,用于后续的目标识别阈值区间的选取 img cv.imread(r"D:\data\123.png") img cv.cvtColor(img, cv.COLOR_BGR2HSV) plt.figure(1), plt.imshow…...

一、计算机硬件选购
计算机硬件选购 一、设备选购1.1 I/O设备1.2 机箱1.3 主板1.3.1 主板芯片组的命名方式1.3.2 主板版型1.3.3 Z790-a(DDR5)主板参数 1.4 CPU1.5 硬盘1.6 显卡1.7 内存条1.8 散热器(水冷)1.9 电源、风扇、网线、插线板1.9.1 电源1.9.2 风扇1.9.3 网线1.9.4 …...
Dockerfile制作LAMP环境镜像
文章目录 使用Dockerfile制作LAMP环境镜像编写Dockerfile不修改默认页面修改默认页面 Start Script目录结构及文件登录私有仓库给镜像打标签上传镜像页面检查检测镜像可用性 使用Dockerfile制作LAMP环境镜像 编写Dockerfile 不修改默认页面 FROM centos:7 MAINTAINER "…...
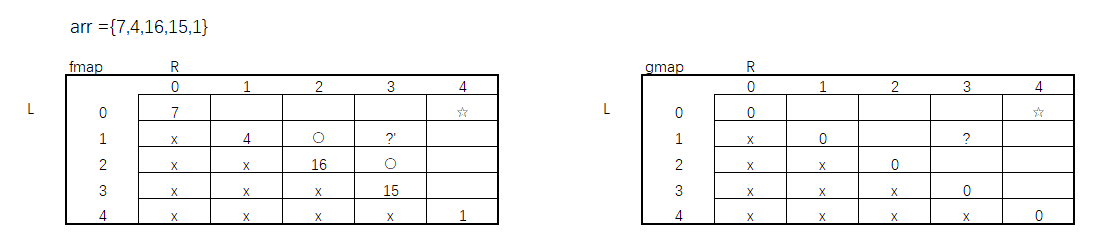
暴力递归转动态规划(二)
上一篇已经简单的介绍了暴力递归如何转动态规划,如果在暴力递归的过程中发现子过程中有重复解的情况,则证明这个暴力递归可以转化成动态规划。 这篇帖子会继续暴力递归转化动态规划的练习,这道题有点难度。 题目 给定一个整型数组arr[]&…...

debian apt error: Package ‘xxx‘ has no installation candidate
新的debian虚拟机可能会出现这个问题。 修改apt的source.list,位于/etc/apt/source.list,添加两行: deb http://deb.debian.org/debian bullseye main deb-src http://deb.debian.org/debian bullseye main执行: sudo apt-get u…...
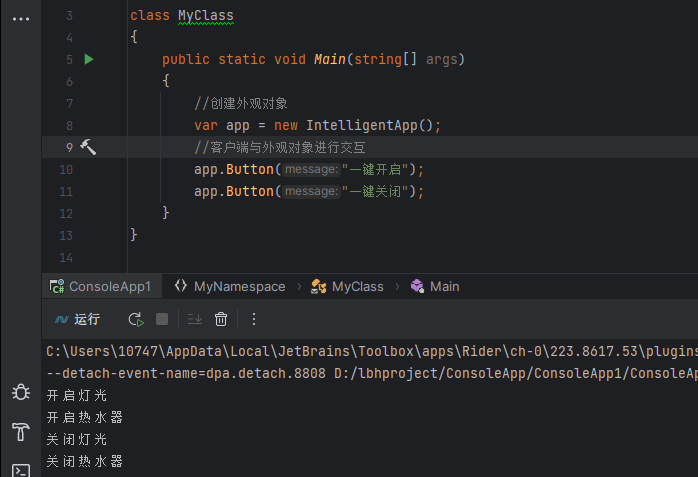
c#设计模式-结构型模式 之 外观模式
概述 外观模式(Facade Pattern)又名门面模式,隐藏系统的复杂性,并向客户端提供了一个客户端可以访问系统的接口。这种类型的设计模式属于结构型模式,它向现有的系统添加一个接口,来隐藏系统的复杂性。该模式…...

Focal Loss-解决样本标签分布不平衡问题
文章目录 背景交叉熵损失函数平衡交叉熵函数 Focal Loss损失函数Focal Loss vs Balanced Cross EntropyWhy does Focal Loss work? 针对VidHOI数据集Reference 背景 Focal Loss由何凯明提出,最初用于图像领域解决数据不平衡造成的模型性能问题。 交叉熵损失函数 …...

运算符(个人学习笔记黑马学习)
算数运算符 加减乘除 #include <iostream> using namespace std;int main() {int a1 10;int a2 20;cout << a1 a2 << endl;cout << a1 - a2 << endl;cout << a1 * a2 << endl;cout << a1 / a2 << endl;/*double a3 …...

开源与专有软件:比较与对比
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

openResty+lua+redis实现接口访问频率限制
openResty简介: OpenResty 是一个基于 Nginx 与 Lua 的高性能 Web 平台,其内部集成了大量精良的 Lua 库、第三方模块以及大多数的依赖项。用于方便地搭建能够处理超高并发、扩展性极高的动态 Web 应用、Web 服务和动态网关。 OpenResty 通过汇聚各种设…...
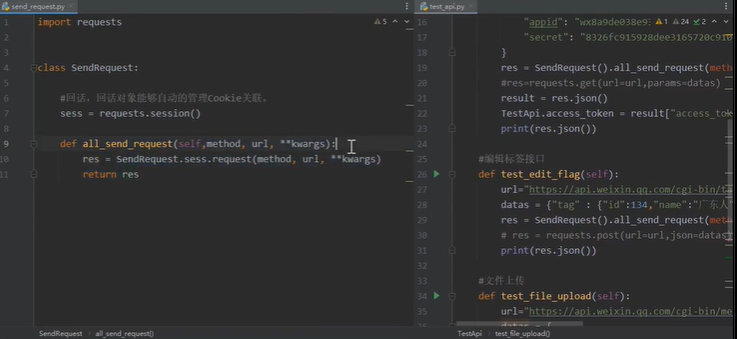
自动化测试(三):接口自动化pytest测试框架
文章目录 1. 接口自动化的实现2. 知识要点及实践2.1 requests.post传递的参数本质2.2 pytest单元测试框架2.2.1 pytest框架简介2.2.2 pytest装饰器2.2.3 断言、allure测试报告2.2.4 接口关联、封装改进YAML动态传参(热加载) 2.3 pytest接口封装ÿ…...

Python --datetime模块
目录 1, 获取datetime时间 2, datetime与timestamp转换 2-1, datetime转timestamp 2-2, timestamp转datetime 3, str格式与datetime转换 3-1, datetime转str格式 3-2, str格式转datetime…...
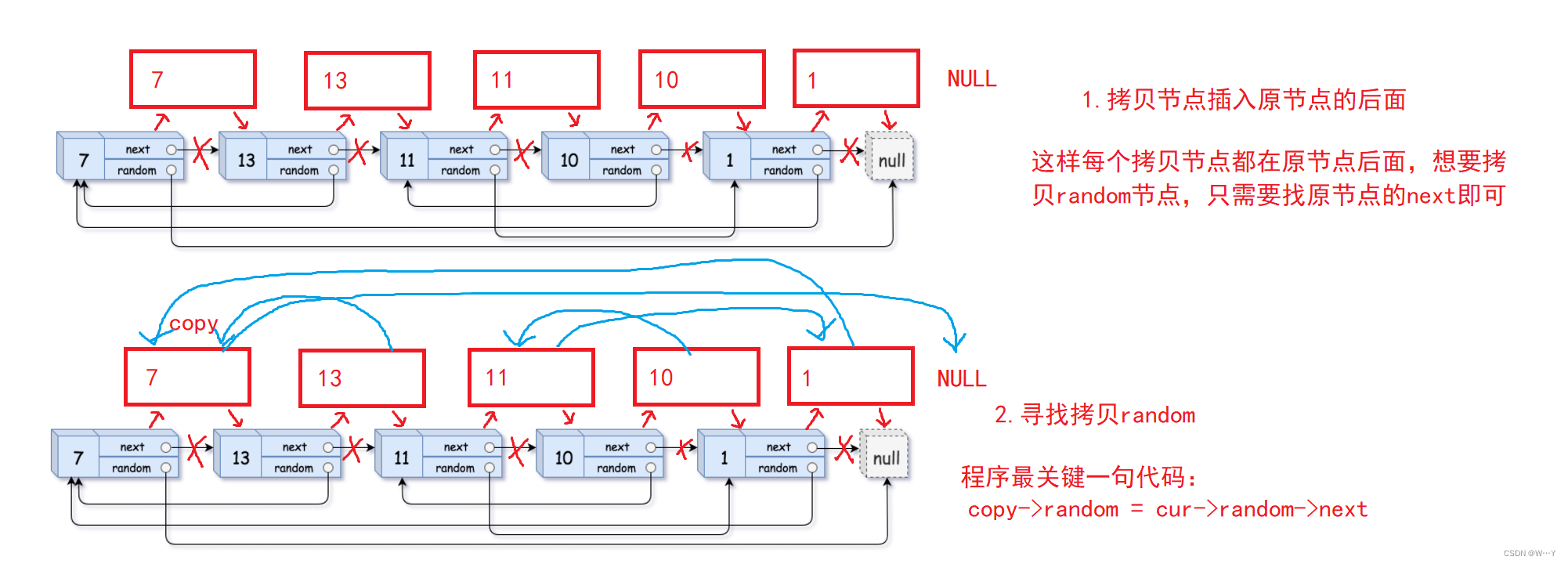
顺序表链表OJ题(3)——【数据结构】
W...Y的主页 😊 代码仓库分享 💕 前言: 今天是链表顺序表OJ练习题最后一次分享,每一次的分享题目的难度也再有所提高,但是我相信大家都是非常机智的,希望看到博主文章能学到东西的可以一键三连关注一下博主…...

【Azure】Virtual Hub vWAN
虚拟 WAN 文档 Azure 虚拟 WAN 是一个网络服务,其中整合了多种网络、安全和路由功能,提供单一操作界面。 我们主要讨论两种连接情况: 通过一个 vWAN 来连接不通的 vNET 和本地网络。以下是一个扩展的拓扑 结合 vhub,可以把两个中…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
