算法通过村第四关-栈白银笔记|括号问题
文章目录
- 前言
- 1. 括号匹配问题
- 2. 最小栈问题
- 3. 最大栈
- 总结
前言
提示:如果让我送给年轻人四个字,就是:量力而行。 量力而行不会失眠,不会啃老,不会为各种考试焦虑。顺其自然活得轻松。其实,量力而行最易大展宏图。
栈在常见的数据结构中也是比较常用的,一些经典的题目对于理解栈很有帮助,就那他们练手吧
1. 括号匹配问题
栈的典型题目,栈常用在括号匹配,表达式计算等等,我看就来看看这个最经典的问题:
参考题目介绍:20. 有效的括号 - 力扣(LeetCode)


对于这个题目来说,还是比较简单的,要处理的问题难题时判断符号是否一组,我们可以先用Hash将所有的符合存储下来,左半边就做key,右半边做value。遍历字符串的时候,遇到左半边符号就入栈,遇到右半边的符号就与栈顶的符号进行比较,不匹配就返回false;
public static boolean isValid(String s) {if (s.length() < 2) {return false;}HashMap<Character, Character> map = new HashMap<Character, Character>();map.put('[', ']');map.put('(', ')');map.put('{', '}');Stack<Character> stack = new Stack<>();for (int i = 0; i < s.length(); i++) {char c = s.charAt(i);if (map.containsKey(c)) {stack.push(c);} else {if (!stack.isEmpty()) {// 拿到栈顶的左括号Character left = stack.pop();Character right = map.get(left);if (right != c) {return false;}} else {return false;}}}return stack.isEmpty();}当然类似的题目还有很多,有难有易,可以多杀杀,挫挫锐气哈哈哈🤣,这里我就不一一举例🌰了
2. 最小栈问题
参考题目介绍:155. 最小栈 - 力扣(LeetCode)

不知到你会不会和我一样题目还没理解什么意思的,别慌,那我们就来看看,这个题要怎么解。我觉得本题的关键在于getMin()到底表示什么,我们可以画一个图;
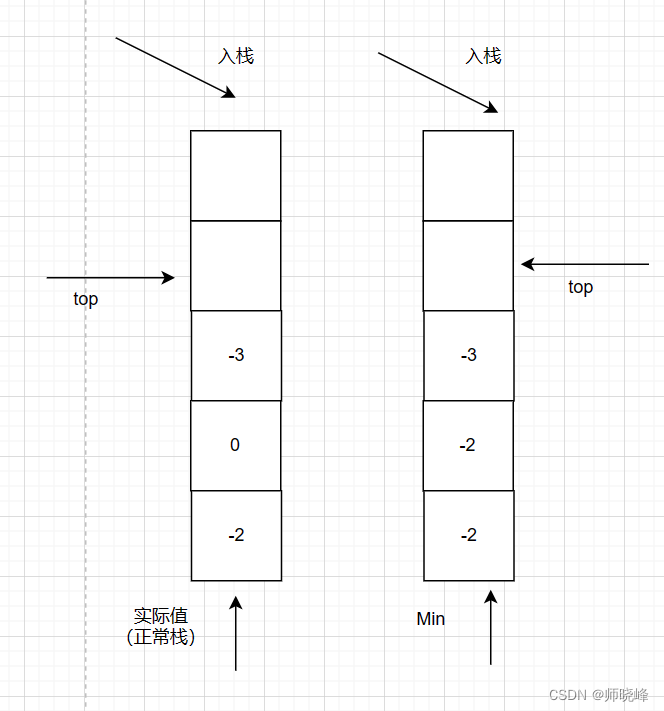
我们看到这个图,大致已经有了思路,Min栈内,中间-2元素,对它的理解就是解题的关键。
题目要求在常数时间内获取到栈中的最小值,也就是我们不能在getMin()的时候去计算,而是直接返回值,也就说只能在push和pop中做一些操作了。
栈的特性时先进后出,这个很重要,我们可以这么做,我们将元素(a)存入栈中的时候,就把当前的最小值(m)记录下来,也就是说如果a时栈顶,最小是就是m,我们可以直接返回。
这样的话我们就可以设计一个数据结构,使得每个元素a与其相应的最小值m时刻保持一致,所以我们需要一个辅助栈,与元素栈插入和删除保持一致,用来存储每个元素对应的最小值。
- 当元素要入栈的时候,我们取当前辅助栈的栈顶元素与之比较,该元素小,就将这个值存入辅助栈中;
- 当一个元素要出栈时,我们把辅助栈的栈顶元素一并出栈
这样的话,在任意时刻,栈内元素的最小值就存储在辅助栈的栈顶元素中。
这样的话代码写起来就非常简单了🤣
class MinStack {private static Stack<Integer> xStack;private static Stack<Integer> minStack;public MinStack() {xStack = new Stack<>();minStack = new Stack<>();// 占位符minStack.push(Integer.MAX_VALUE);}public void push(int val) {xStack.push(val);minStack.push(Math.min(val,minStack.peek()));}public void pop() {xStack.pop();minStack.pop();}public int top() {return xStack.peek();}public int getMin() {return minStack.peek();}
}/*** Your MinStack object will be instantiated and called as such:* MinStack obj = new MinStack();* obj.push(val);* obj.pop();* int param_3 = obj.top();* int param_4 = obj.getMin();*/
有最小栈那会不会有最大栈呢?哈哈哈,他来了
3. 最大栈
参考题目介绍:716. 最大栈 - 力扣(LeetCode)
设计一个最大栈数据结构,及支持栈操作,有支持查找栈中最大元素。

这个题和上一题相反,处理方法上一致,一个普通的栈可以支持前三种操作,push(x),pop()和top(),这里我们需要考虑的是后面的操作peekMax()和popMax()。
对于peekMax(),我们可以用另一个栈来存储每个位置对应的最大值,比如第一个栈的元素为[2,1,5,3,9],那么第二个栈的元素就是[2,2,5,5,9]。在push(x)操作时,只需要将第二个栈顶元素和x的最大值入栈就行,而pop()操作只需要将第二个栈进行出栈。
对于popMax(),由于我们指导当前栈中最大元素值,我们就可以将两个栈同时出栈,并存储第一个栈出栈的所有值。当某个时刻第一个栈中的出栈元素等于当前栈中的最大值时,我们就找到了最大元素。此时我们将之前的第一个栈的所有元素重新入栈,并同步更新到第二栈中,就完成了popMax()操作;
代码展示如下:
import java.util.Stack;class MaxStack {public static Stack<Integer> xStack;public static Stack<Integer> maxStack;public MaxStack() {xStack = new Stack<Integer>();maxStack = new Stack<Integer>();}public void push(int val) {xStack.push(val);int max = maxStack.isEmpty() ? val : maxStack.peek();maxStack.push(max > val ? max : val);}public int pop() {maxStack.pop();return xStack.pop();}public int top() {return xStack.peek();}public int peekMax() {return maxStack.peek();}public int popMax() {int max = peekMax();Stack<Integer> stack = new Stack<Integer>();while(top() != max){stack.push(pop());}pop();while(!stack.isEmpty()){push(stack.pop());}return max;}}
总结
提示:栈的操作有时需要一个辅助栈,来帮助解决问题。
相关文章:

算法通过村第四关-栈白银笔记|括号问题
文章目录 前言1. 括号匹配问题2. 最小栈问题3. 最大栈 总结 前言 提示:如果让我送给年轻人四个字,就是:量力而行。 量力而行不会失眠,不会啃老,不会为各种考试焦虑。顺其自然活得轻松。其实,量力而行最易大…...
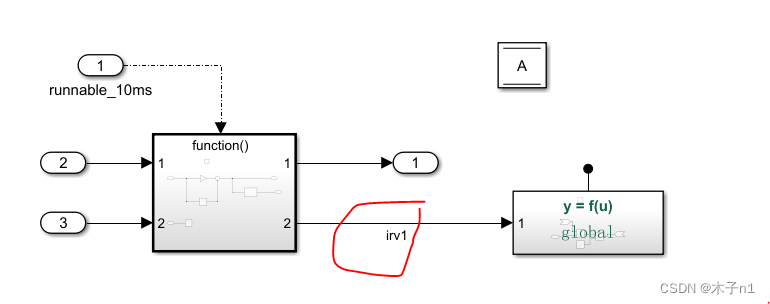
基于MATLAB开发AUTOSAR软件应用层Code mapping专题-part 6 Data Transfers标签页介绍
这篇文章我们介绍下Data Transfers页的配置,这里边包含的内容是IRV,我之前的文章里有讲解过IRV就是 Inter-Runnable Variables,内部runnable的之间传递数据的变量,在讲解Data Store memory的文章里我们提到了,irv也可以使用Data Store memory的方式来实现,我们先看下IRV如何…...
HDLBits-Verilog学习记录 | Verilog Language-Vectors
文章目录 11.vectors | vector012.vectors in more detail | vector113.Vector part select | Vector214.Bitwise operators | Vectorgates15.Four-input gates | Gates416.Vector concatenation operator | Vector317.Vector reversal 1 | Vectorr18. Replication operator | …...

彻底搞懂 PHP 运算符 ?: 和 ??
文章目录 快速掌握?: 短三元运算符?? NULL 合并运算符 附上官方文档查阅方式 快速掌握 ?: 短三元运算符 ?: 称之为短三元运算符,它是我们熟悉的三元运算符(也叫做条件运算符)的一种特殊写法,也就是省略了三元运算符中间的部…...

贝叶斯人工智能大脑与 ChatGPT
文章目录 一、前言二、主要内容 🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 论文地址:https://arxiv.org/abs/2308.14732 这篇论文旨在研究 Chat Generative Pre-trained Transformer(ChatGPT)在贝叶斯…...

适应高速率网络设备的-2.5G/5G/10G网络变压器/网络滤波器介绍
Hqst盈盛(华强盛)电子导读:在高速发展的互联网/物联网时代,为满足高网速的网络数据传输需求,网络设备在制造中也要选用合适的网络变压器/滤波器产品,有哪些可供选择的高速率网络变压器产品也是广大采购人员…...
「Redis」1. 数据类型的底层实现
前言:在这篇博文中,我们将简单总结在面试中怎么回答Redis数据类型的底层实现。 因为面试时间就那么点,言简意赅的描述自己会的知识显得尤为重要‼️ 文章目录 0.1. String 的底层实现原理0.2. 列表的底层实现原理0.3. 字典的底层实现原理0.4.…...
Win11共享文件,能发现主机但无法访问,提示找不到网络路径
加密长度选择如下: 参考以下链接: Redirectinghttps://answers.microsoft.com/zh-hans/windows/forum/all/win11%E8%AE%BE%E7%BD%AE%E6%96%87%E4%BB%B6%E5%A4%B9/554343a9-d963-449a-aa59-ce1e6f7c8982?tabAllReplies#tabs...

ROS中使用Navigation报错信息
在ROS中使用遇到了几个Navigation报错信息,在这里进行下记录: [ WARN] [1688134727.429227824]: The origin for the sensor at (7.35, 13.12) is out of map bounds. So, the costmap cannot raytrace for it. 解决办法: [ WARN] [16881…...
three.js(六):自适应设备分辨率
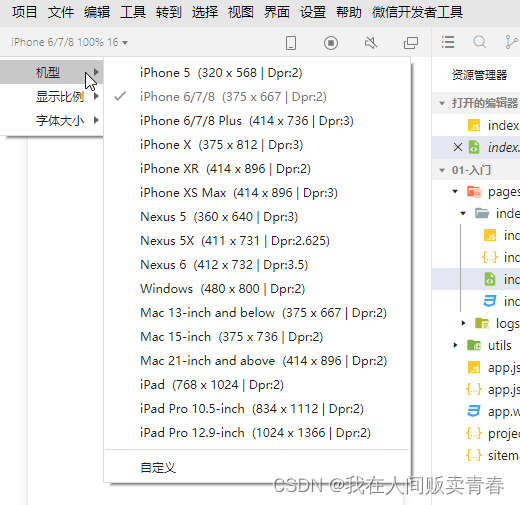
自适应设备分辨率 当今大多数的PC端和移动端显示器都是HD-DPI显示器。HD-DPI 是High Definition-Dots Per Inch 的简称,意思是高分辨率显示器。不同设备的显示器的分辨率是不一样的。 以上图中的iPhone6/7/8 为例:375*667 代表的手机的屏幕的物理尺寸&a…...
Kubernetes对象深入学习之五:TypeMeta无效之谜
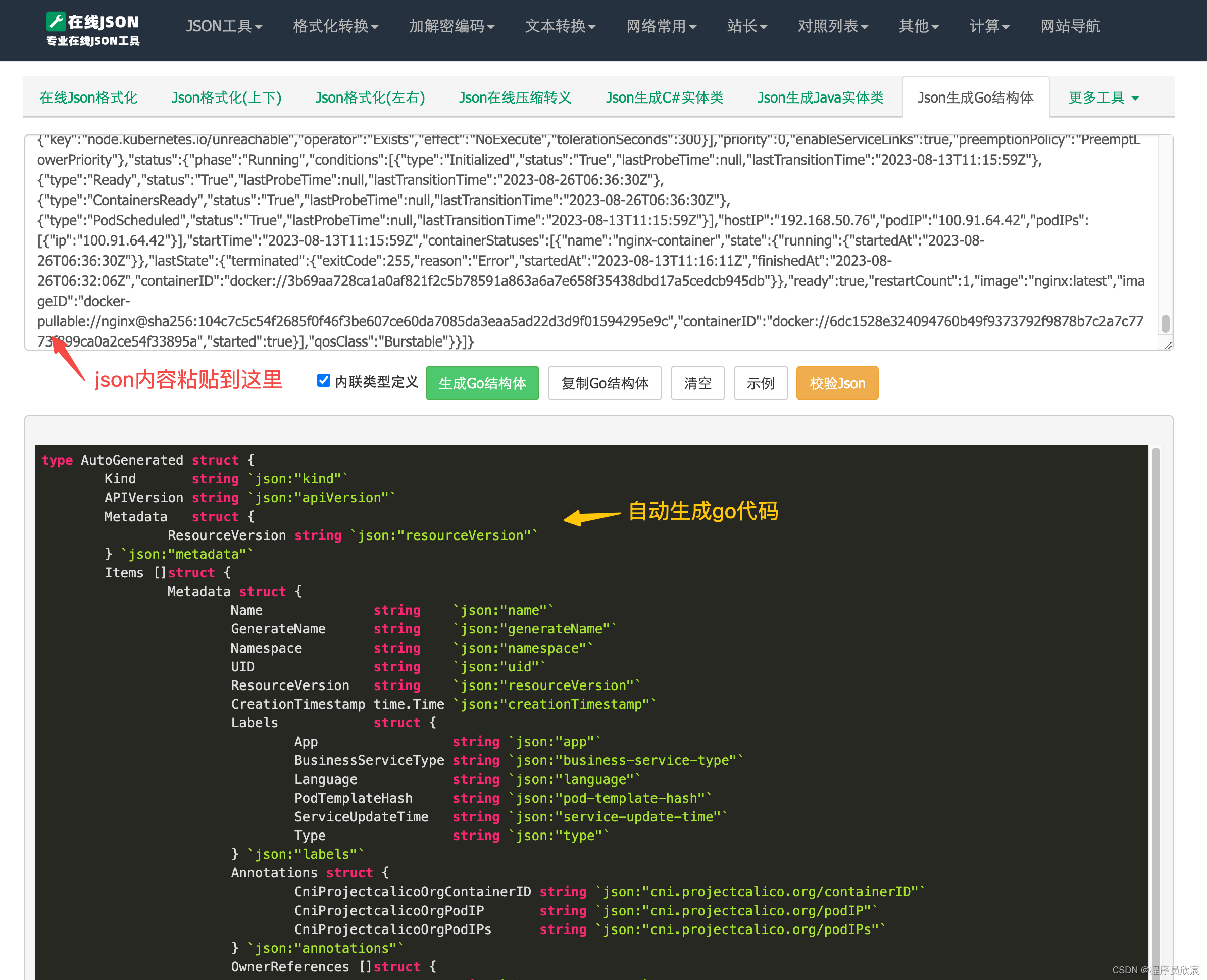
欢迎访问我的GitHub 这里分类和汇总了欣宸的全部原创(含配套源码):https://github.com/zq2599/blog_demos 本篇概览 本文是《Kubernetes对象深入学习之五》系列的第五篇,从前文的分析也能看出,代表对象类型的schema.ObjectKind,于…...
Gitlab设置中文
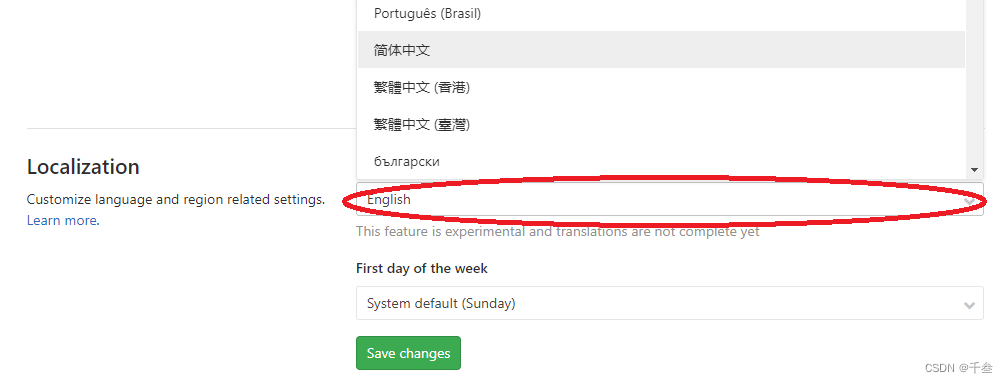
1. 打开设置 2.选择首选项Preferences 3. 下滑选择本地化选项Localization,设置简体中文,然后保存更改save changes。刷新网页即可。...

【微服务部署】05-安全:强制HTTPS
文章目录 安全 : 强制HTTPS的两种方式1. Ingress配置重定向2. 应用程序配置3. Ingress配置4. 应用程序配置代码总结 安全 : 强制HTTPS的两种方式 互联网发展中,安全是非常重要的,由其是现在HTTPS非常普及的情况下,应用程序在公网上一般都会被…...

Config:服务端连接Git配置
创建子模块 Pom文件 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org…...

c++学习 之 类和对象 public , protected ,private
前言 在C中,访问控制修饰符(Access Control Modifiers)用于控制类的成员(成员变量和成员函数)的访问权限。这些修饰符分为三种:public、protected和private。它们定义了成员可以在何处访问,具体…...

ECharts图表动态修改series显示隐藏
文章目录 1、前言2、思路3、实现 1、前言 最近做的大数据平台,里面很多部分用到了ECharts,其中有个功能,要求将图表分组,根据用户选择的组,来确定ECharts要显示那些线条和柱子,也就是动态的显示option.seri…...
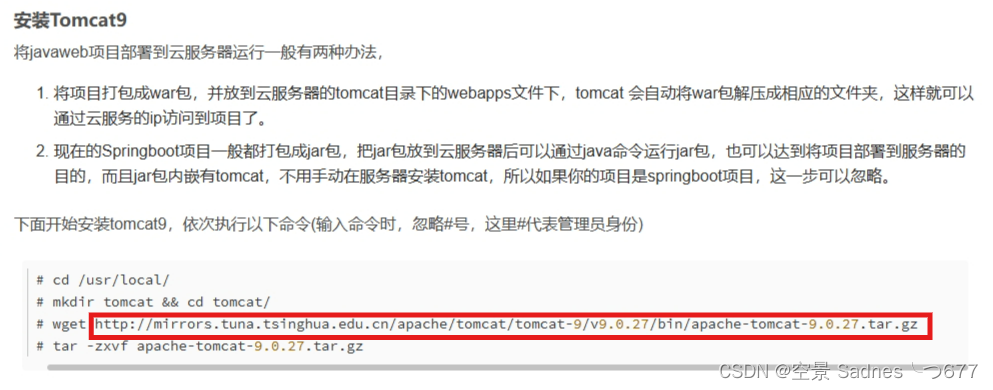
云服务器(Centos7系统)配置JAVA+mysql+tomcat 环境
文章主要内容来源云服务器(Centos7系统)部署javaweb项目(二)配置JAVAmysqltomcat 环境_man_zuo的博客-CSDN博客 模仿途中遇到的问题 连接无效 有时连接无法下载,可能是过期了,将其更换为官网给的下载连接即…...
)
【计算机视觉 | 目标检测】目标检测常用数据集及其介绍(四)
文章目录 一、JTA (Joint Track Auto)二、AVD (Active Vision Dataset)三、ExDark (Exclusively Dark Image Dataset)四、InteriorNet五、ScanRefer Dataset六、FlickrLogos-32七、SIXray八、Clear Weather (DENSE)九、DVQA (Data Visualizations via Question Answering)十、M…...

Dockerfile制作镜像与搭建LAMP环境
一.编写Dockerfile制作Web应用系统nginx镜像,生成镜像nginx:v1.1,并推送其到私有仓库。具体要求如下: (1)基于centos基础镜像; (2)指定作者信息; (3ÿ…...

Linux系统中查看端口的方法
一、使用netstat命令 netstat命令是一种非常实用的命令,可以用来显示网络连接、路由表、网络接口和网络统计信息等。它还可以用来显示系统中正在监听的端口。要查看端口,只需在终端中输入以下命令: netstat -tuln 这个命令的意思是列出所有…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
