NOI2015D. 荷马史诗
荷马史诗
题目描述
追逐影子的人,自己就是影子。 ——荷马
Allison 最近迷上了文学。她喜欢在一个慵懒的午后,细细地品上一杯卡布奇诺,静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了,Allison 想通过一种编码方式使得它变得短一些。
一部《荷马史诗》中有 nnn 种不同的单词,从 111 到 nnn 进行编号。其中第 iii 种单词出现的总次数为 wiw_iwi。Allison 想要用 kkk 进制串 sis_isi 来替换第 iii 种单词,使得其满足如下要求: 对于任意的 1≤i,j≤n, i≠j1 \leq i,j \leq n, \ i \neq j1≤i,j≤n, i=j,都有:sis_isi 不是 sjs_jsj 的前缀。
现在 Allison 想要知道,如何选择 sis_isi,才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下,Allison 还想知道最长的 sis_isi 的最短长度是多少?
一些定义:
一个字符串被称为 kkk 进制字符串,当且仅当它的每个字符是 000 到 k−1k−1k−1 之间(包括 000 和 k−1k−1k−1)的整数。
字符串 Str1\text{Str}_1Str1 被称为字符串 Str2\text{Str}_2Str2 的前缀,当且仅当:存在 1≤t≤m1 \leq t \leq m1≤t≤m,使得 Str1=Str2[1…t]\text{Str}_1=\text{Str}_2[1 \ldots t]Str1=Str2[1…t]。其中,mmm 是字符串 Str2\text{Str}_2Str2 的长度,Str2[1…t]\text{Str}_2[1 \ldots t]Str2[1…t] 表示 Str2\text{Str}_2Str2 的前 ttt 个字符组成的字符串。
输入格式
输入文件的第一行包含两个正整数 n,kn,kn,k,中间用单个空格隔开,表示共有 nnn 种单词,需要使用 kkk 进制字符串进行替换。
接下来 nnn 行,第 i+1i+1i+1 行包含 111 个非负整数 wiw_iwi,表示第 iii 种单词的出现次数。
输出格式
输出文件包括两行。
第一行输出一个整数,为《荷马史诗》经过重新编码以后的最短长度。
第二行输出一个整数,为保证最短总长度的情况下,最长字符串 sis_isi 的最短长度。
数据范围与提示
限制与约定
| Case # | nnn 的规模 | kkk 的规模 | 附加限制 |
|---|---|---|---|
| 1 | n=3n = 3n=3 | k=2k = 2k=2 | - |
| 2 | n=5n = 5n=5 | ||
| 3 | n=16n = 16n=16 | 所有 wiw_iwi 均相等 | |
| 4 | n=1000n = 1000n=1000 | wiw_iwi 在取值范围内均匀随机 | |
| 5 | - | ||
| 6 | n=100000n = 100000n=100000 | ||
| 7 | 所有 wiw_iwi 均相等 | ||
| 8 | - | ||
| 9 | n=7n = 7n=7 | k=3k = 3k=3 | |
| 10 | n=16n = 16n=16 | 所有 wiw_iwi 均相等 | |
| 11 | n=1001n = 1001n=1001 | ||
| 12 | n=99999n = 99999n=99999 | k=4k = 4k=4 | |
| 13 | n=100000n = 100000n=100000 | - | |
| 14 | |||
| 15 | n=1000n = 1000n=1000 | k=5k = 5k=5 | |
| 16 | n=100000n = 100000n=100000 | k=7k = 7k=7 | wiw_iwi 在取值范围内均匀随机 |
| 17 | - | ||
| 18 | k=8k = 8k=8 | wiw_iwi 在取值范围内均匀随机 | |
| 19 | k=9k = 9k=9 | - | |
| 20 |
对于所有数据,保证 2≤n≤100000, 2≤k≤9, 0<wi≤10112 \leq n \leq 100000, \ 2 \leq k \leq 9, \ 0 \lt w_i \leq 10^{11}2≤n≤100000, 2≤k≤9, 0<wi≤1011。选手请注意使用 646464 位整数进行输入输出、存储和计算。
评分方式
对于每个测试点:
若输出文件的第 111 行正确,得到该测试点 40%40\%40% 的分数;
若输出文件完全正确,得到该测试点 100%100\%100% 的分数。
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#define ll long long
using namespace std;
struct node
{ll w,h;node(){w=0,h=0;}node(ll w,ll h):w(w),h(h){}bool operator <(const node &a)const{return a.w==w?h>a.h:w>a.w;}
};
ll ans;
priority_queue<node>q;
int main()
{ll n,k;ans=0;scanf("%lld%lld",&n,&k);for(int i=1;i<=n;i++){ll w;scanf("%lld",&w);q.push(node(w,1));}while((q.size()-1)%(k-1)!=0)q.push(node(0,1));while(q.size()>=k){ll h=-1;ll w=0;for(int i=1;i<=k;++i){node t=q.top();q.pop();h=max(h,t.h);w+=t.w;}ans+=w;q.push(node(w,h+1));}printf("%lld\n%lld\n",ans,q.top().h-1);return 0;
}
相关文章:

NOI2015D. 荷马史诗
荷马史诗 题目描述 追逐影子的人,自己就是影子。 ——荷马 Allison 最近迷上了文学。她喜欢在一个慵懒的午后,细细地品上一杯卡布奇诺,静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是…...
03详细讲解未补充)
并法编程(集合类不安全)03详细讲解未补充
还未补充...

软考:中级软件设计师:大数据
软考:中级软件设计师:大数据 提示:系列被面试官问的问题,我自己当时不会,所以下来自己复盘一下,认真学习和总结,以应对未来更多的可能性 关于互联网大厂的笔试面试,都是需要细心准备的 &#x…...
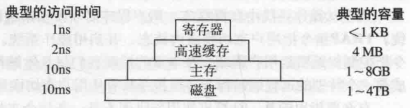
【持续更新中】QAGroup1
OVERVIEW Q&AGroup1一、语言基础1.C语言(1)含参数的宏与函数的不同点(2)sizeof与strlen的区别(3)大/小端(4)strcpy与memcpy的区别(5)extern与static的区别…...
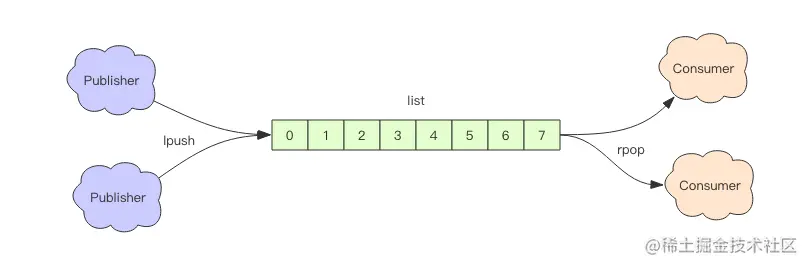
redis应用 2:延时队列
我们平时习惯于使用 Rabbitmq 和 Kafka 作为消息队列中间件,来给应用程序之间增加异步消息传递功能。这两个中间件都是专业的消息队列中间件,特性之多超出了大多数人的理解能力。 使用过 Rabbitmq 的同学知道它使用起来有多复杂,发消息之前要…...

ChatGPT AIGC 实现动态组合图的用法
数据分析组合图,即在一张图表中组合使用多种图形类型(如柱状图、折线图、饼图等),可以在同一视图中展示多个维度或多个量度的数据,帮助数据分析师或决策者更好地理解和解释数据。 组合图的功能和作用主要包括: 提供信息视角:组合图可以对比不同类型的数据,展现数据间的…...

【网站】解压放松的治愈白噪音ASMR
70年代中期国际上新创立的无穷维Schwartz广泛函数理论,应用所严加安研究员是建立和完善该理论的数学框架的主要贡献者之一,他与法国科学院通讯院士Meyer教授提出的框架被称为Meyer-Yan空间。他与Kondratiev等新近发表的论文建立了完善的无穷维非高斯分析…...

算法通过村第四关-栈白银笔记|括号问题
文章目录 前言1. 括号匹配问题2. 最小栈问题3. 最大栈 总结 前言 提示:如果让我送给年轻人四个字,就是:量力而行。 量力而行不会失眠,不会啃老,不会为各种考试焦虑。顺其自然活得轻松。其实,量力而行最易大…...
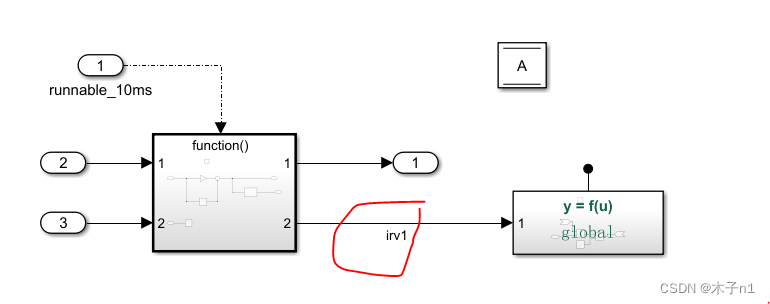
基于MATLAB开发AUTOSAR软件应用层Code mapping专题-part 6 Data Transfers标签页介绍
这篇文章我们介绍下Data Transfers页的配置,这里边包含的内容是IRV,我之前的文章里有讲解过IRV就是 Inter-Runnable Variables,内部runnable的之间传递数据的变量,在讲解Data Store memory的文章里我们提到了,irv也可以使用Data Store memory的方式来实现,我们先看下IRV如何…...
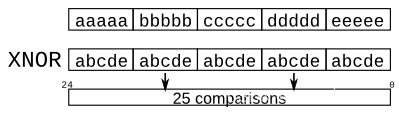
HDLBits-Verilog学习记录 | Verilog Language-Vectors
文章目录 11.vectors | vector012.vectors in more detail | vector113.Vector part select | Vector214.Bitwise operators | Vectorgates15.Four-input gates | Gates416.Vector concatenation operator | Vector317.Vector reversal 1 | Vectorr18. Replication operator | …...

彻底搞懂 PHP 运算符 ?: 和 ??
文章目录 快速掌握?: 短三元运算符?? NULL 合并运算符 附上官方文档查阅方式 快速掌握 ?: 短三元运算符 ?: 称之为短三元运算符,它是我们熟悉的三元运算符(也叫做条件运算符)的一种特殊写法,也就是省略了三元运算符中间的部…...

贝叶斯人工智能大脑与 ChatGPT
文章目录 一、前言二、主要内容 🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 论文地址:https://arxiv.org/abs/2308.14732 这篇论文旨在研究 Chat Generative Pre-trained Transformer(ChatGPT)在贝叶斯…...

适应高速率网络设备的-2.5G/5G/10G网络变压器/网络滤波器介绍
Hqst盈盛(华强盛)电子导读:在高速发展的互联网/物联网时代,为满足高网速的网络数据传输需求,网络设备在制造中也要选用合适的网络变压器/滤波器产品,有哪些可供选择的高速率网络变压器产品也是广大采购人员…...
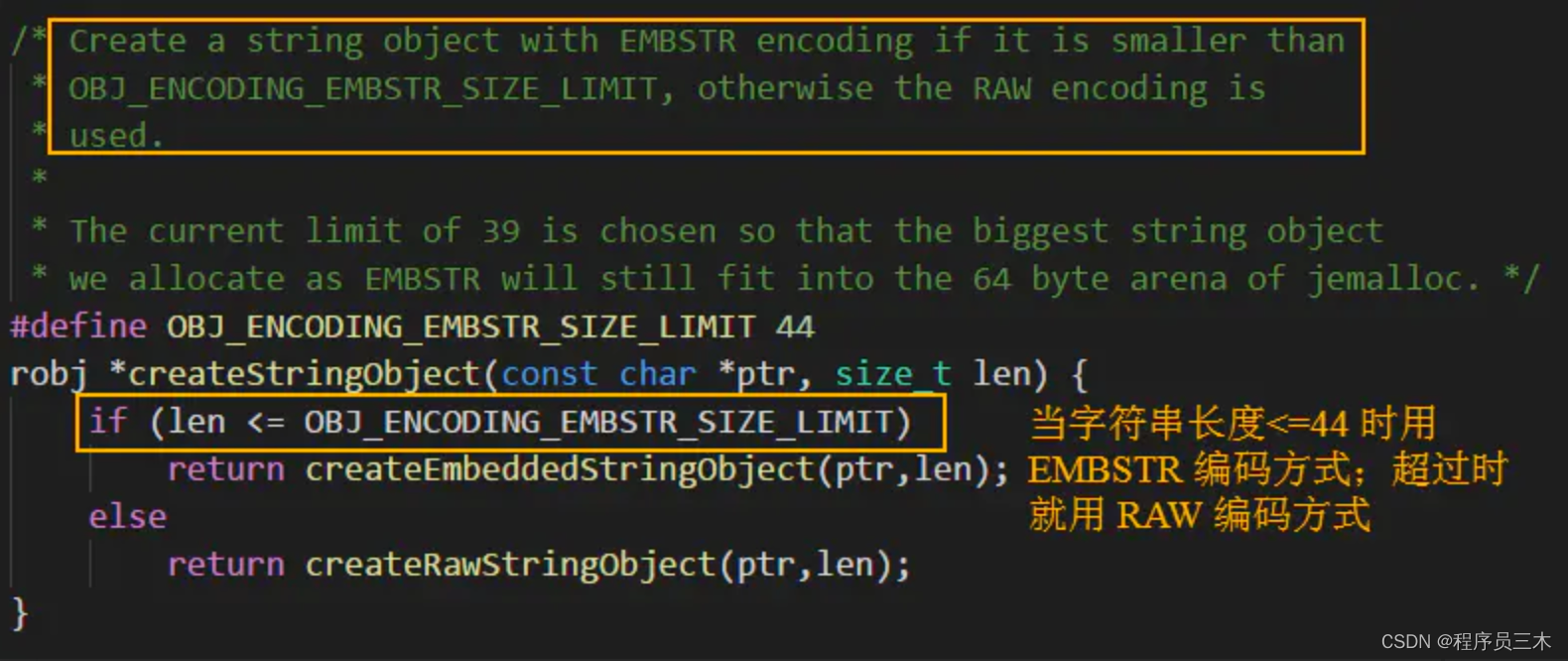
「Redis」1. 数据类型的底层实现
前言:在这篇博文中,我们将简单总结在面试中怎么回答Redis数据类型的底层实现。 因为面试时间就那么点,言简意赅的描述自己会的知识显得尤为重要‼️ 文章目录 0.1. String 的底层实现原理0.2. 列表的底层实现原理0.3. 字典的底层实现原理0.4.…...
Win11共享文件,能发现主机但无法访问,提示找不到网络路径
加密长度选择如下: 参考以下链接: Redirectinghttps://answers.microsoft.com/zh-hans/windows/forum/all/win11%E8%AE%BE%E7%BD%AE%E6%96%87%E4%BB%B6%E5%A4%B9/554343a9-d963-449a-aa59-ce1e6f7c8982?tabAllReplies#tabs...

ROS中使用Navigation报错信息
在ROS中使用遇到了几个Navigation报错信息,在这里进行下记录: [ WARN] [1688134727.429227824]: The origin for the sensor at (7.35, 13.12) is out of map bounds. So, the costmap cannot raytrace for it. 解决办法: [ WARN] [16881…...
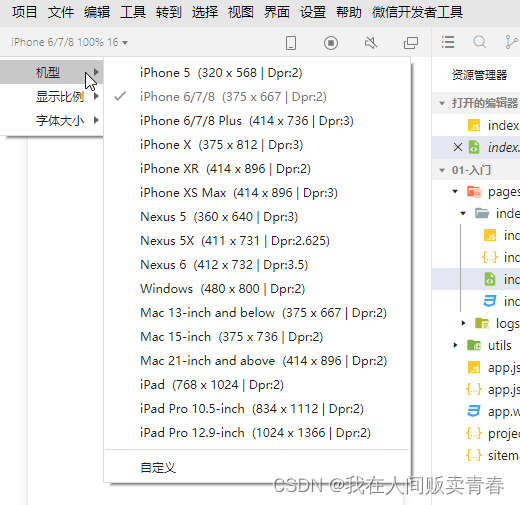
three.js(六):自适应设备分辨率
自适应设备分辨率 当今大多数的PC端和移动端显示器都是HD-DPI显示器。HD-DPI 是High Definition-Dots Per Inch 的简称,意思是高分辨率显示器。不同设备的显示器的分辨率是不一样的。 以上图中的iPhone6/7/8 为例:375*667 代表的手机的屏幕的物理尺寸&a…...
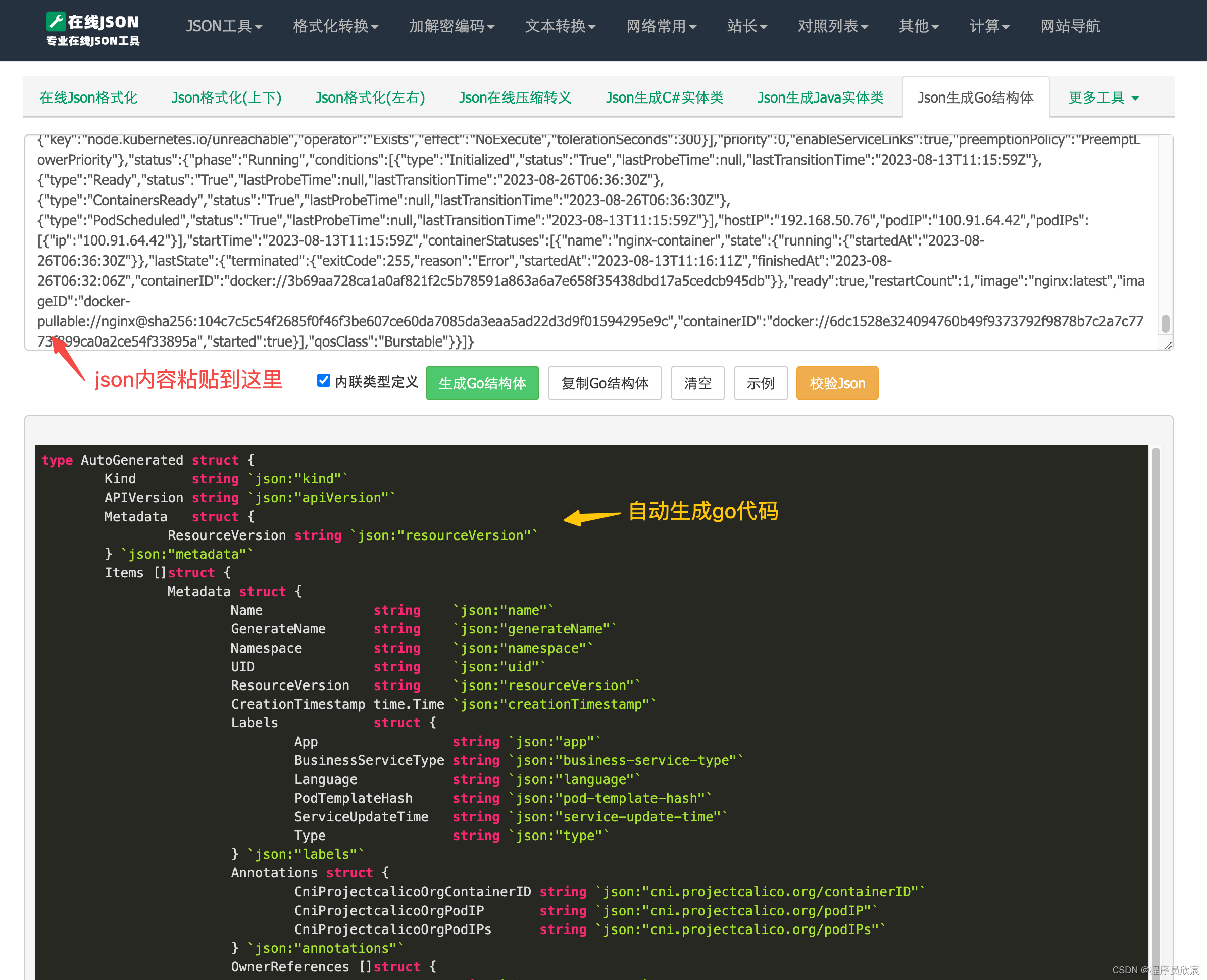
Kubernetes对象深入学习之五:TypeMeta无效之谜
欢迎访问我的GitHub 这里分类和汇总了欣宸的全部原创(含配套源码):https://github.com/zq2599/blog_demos 本篇概览 本文是《Kubernetes对象深入学习之五》系列的第五篇,从前文的分析也能看出,代表对象类型的schema.ObjectKind,于…...
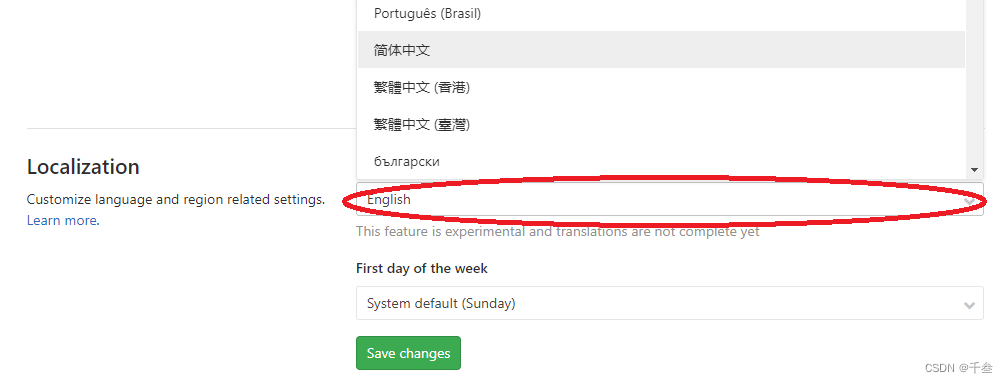
Gitlab设置中文
1. 打开设置 2.选择首选项Preferences 3. 下滑选择本地化选项Localization,设置简体中文,然后保存更改save changes。刷新网页即可。...

【微服务部署】05-安全:强制HTTPS
文章目录 安全 : 强制HTTPS的两种方式1. Ingress配置重定向2. 应用程序配置3. Ingress配置4. 应用程序配置代码总结 安全 : 强制HTTPS的两种方式 互联网发展中,安全是非常重要的,由其是现在HTTPS非常普及的情况下,应用程序在公网上一般都会被…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
