数学建模:CRITIC赋权法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛
CRITIC赋权法
算法流程
- 构建原始数据矩阵 X X X,他是一个 m ∗ n m * n m∗n 的矩阵, m m m 表示评价对象个数, n n n 表示指标个数
- 对原始数据矩阵进行正向化处理
- 计算矩阵的变异性,即计算矩阵的**标准差:**得到的 S i S_i Si 表示 第 i i i 个指标的标准差
{ x ˉ j = 1 n ∑ i = 1 n x i j S j = ∑ i = 1 n ( x i j − x ˉ j ) 2 n − 1 \left\{\begin{array}{rcl}\mathrm{\bar x_j~=~\frac1n~\sum_{i=1}^nx_{ij}}\\\\\mathrm{S_j~=\sqrt{\frac{\sum_{i=1}^n\left(x_{ij}~-\bar x_j~\right)^2}{n-1}}}\end{array}\right. ⎩ ⎨ ⎧xˉj = n1 ∑i=1nxijSj =n−1∑i=1n(xij −xˉj )2
- 描述指标的冲突性,首先计算指标之间两两的相关系数矩阵,然后计算指标的冲突性:
- 求相关系数矩阵可以直接调用matlab的
corr函数
- 求相关系数矩阵可以直接调用matlab的
R j = ∑ i = 1 n ( 1 − r i j ) \mathrm{R_j~=\sum_{i=1}^n(1-r_{ij})} Rj =i=1∑n(1−rij)
- 计算指标的信息承重量:
C j = S j ∑ i = 1 n ( 1 − r i j ) = S j × R j \mathrm{C_j~=S_j~\sum_{i=1}^n~(1-r_{ij}~)=S_j~\times R_j} Cj =Sj i=1∑n (1−rij )=Sj ×Rj
- 计算每个指标的客观权重:
W j = C j ∑ j = 1 p C j \mathrm{W_j=\frac{C_j}{\sum_{j=1}^pC_j}} Wj=∑j=1pCjCj
代码实现
%%对比性
function [Score,w]=mfunc_CRITIC(data1)% CRITIC方法:求解每个指标对应的客观权重算法% paramts: % data1: 原始数据矩阵,(m,n) m为评价对象,n为评价指标% returns:% Score:每个评价对象的综合得分% w: 所有指标的客观权重% 计算标准差STD=std(data1);%%矛盾性r=corr(data1);%计算指标间的相关系数f=sum(1-r);%%信息承载量c=STD.*f;%计算所有指标的权重w=c/sum(c);%计算得分[m,~]=size(data1);data= data1 ./ repmat(sum(data1.*data1) .^ 0.5, m, 1); %矩阵归一化% data=mapminmax(data1',0.002,1);%标准化到0.002-1区间% data=data';s=data*w';Score=100*s/max(s);
end
相关文章:

数学建模:CRITIC赋权法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 CRITIC赋权法 算法流程 构建原始数据矩阵 X X X,他是一个 m ∗ n m * n m∗n 的矩阵, m m m 表示评价对象个数, n n n 表示指标个数对原始数据矩阵进行正向化处理计算…...

Facebook message tag 使用攻略
Messenger 讯息传不出去?无法发送FB 讯息给非好友? 2020年3月,Facebook 为了防止用户被过多的推广或垃圾讯息困扰而更新使用条款,现在商家要用FB传讯息给所有人(包括非好友),应该使用 Facebook …...

气传导耳机哪个品牌比较好?综合表现很不错的气传导耳机推荐
气传导耳机不仅能够提升幸福感还能听到周围环境声,大大提高安全性。如果你在寻找一款高品质的气传导耳机,又不知从何入手时,不要担心,我已经为你精心挑选了四款市面上综合表现很不错的气传导耳机,让你享受更好的音质…...

Rabbitmq的消息转换器
Spring会把你发送的消息序列化为字节发送给MQ,接收消息的时候,还会把字节反序列化为Java对象 ,只不过,默认情况下Spring采用的序列化方式是JDK序列化。众所周知,JDK序列化存在下列问题: 数据体积过大 有安全漏洞 可读…...

nvidia-docker的使用
拉取镜像 docker pull nvidia/cuda可能出现的问题 问题描述 Error response from daemon: manifest for nvidia/cuda:latest not found: manifest unknown: manifest解决方法: 为找到正确且合适的docker镜像版本 在supported-tags中找到与自己系统对应的cuda版本…...
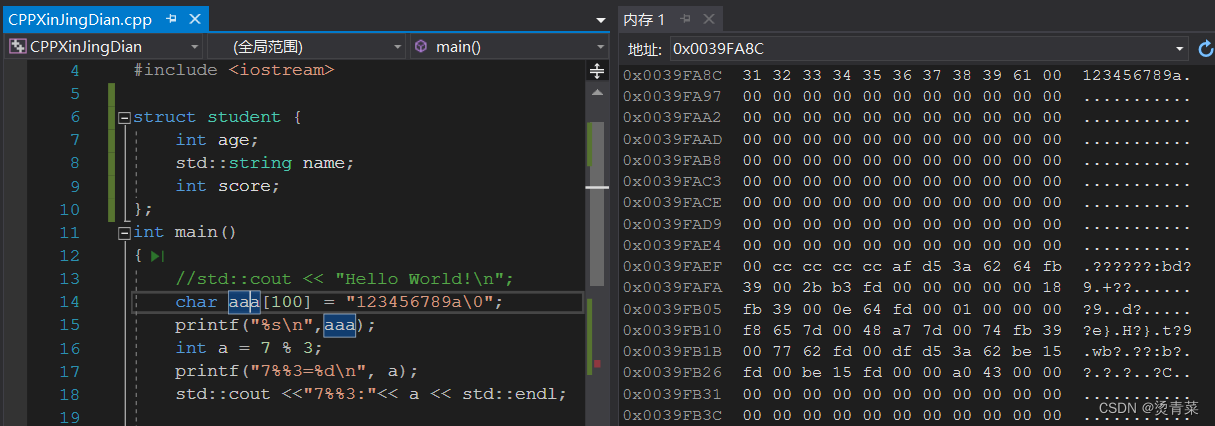
C++新经典 | C语言
目录 一、基础之查漏补缺 1.float精度问题 2.字符型数据 3.变量初值问题 4.赋值&初始化 5.头文件之<> VS " " 6.逻辑运算 7.数组 7.1 二维数组初始化 7.2 字符数组 8.字符串处理函数 8.1 strcat 8.2 strcpy 8.3 strcmp 8.4 strlen 9.函数 …...
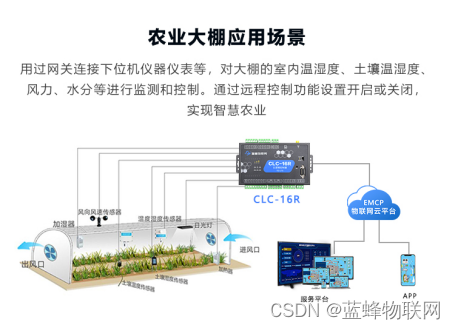
物联网智慧种植农业大棚系统
一、项目背景 智慧农业是是将物联网技术和农业生产箱管理的新型农业,依托部署在农业生产现场的各种传感节点,以物联网网关为通道形成数据传输网络,可以实现控制柜、环境监测传感器、气象监测机器等设备的远程监控,达到及时高校的…...

TabBar组件如何跳转页面?
1、先引入 2、假数据 const tabs [{key: home,title: 首页,icon: <AppOutline />,badge: Badge.dot,},{key: todo,title: 待办,icon: <UnorderedListOutline />,badge: 5,},{key: message,title: 消息,icon: (active: boolean) >active ? <MessageFill /&…...

Vue.js中,router和route
<div class"search">{{$route.params.things}}<van-nav-bar fixed title"商品列表" left-arrow click-left"$router.go(-1)" /><van-searchreadonlyshape"round"background"#ffffff"value"手机"sh…...

【微服务】07-缓存
文章目录 为不同的场景设计合适的缓存策略1. 缓存是什么2. 缓存的场景3. 缓存的策略4. 缓存位置5. 缓存实现的要点6. 注意问题7. 使用的组件8. 内存缓存和分布式缓存区别 总结 为不同的场景设计合适的缓存策略 1. 缓存是什么 缓存是计算结果的“临时”存储和重复使用缓存本质…...

权限校验中的“双token”方案
1. 双Token中的两个token分别是什么? 1.1 access_token 1.2 fresh_token 2. 为什么需要双token?一个token不行吗? 答: 两个token的职责不同。其中,access_token是在每次请求的时候携带给后端进行权限校验ÿ…...

TensorFlow的基本概念
TensorFlow 是由 Google 开发的开源机器学习框架,其基本概念如下: 1. 张量(Tensor):TensorFlow 中最基本的数据结构,是多维数组,可以理解为向量或矩阵的推广。常见的张量有常量张量、变量张量和…...
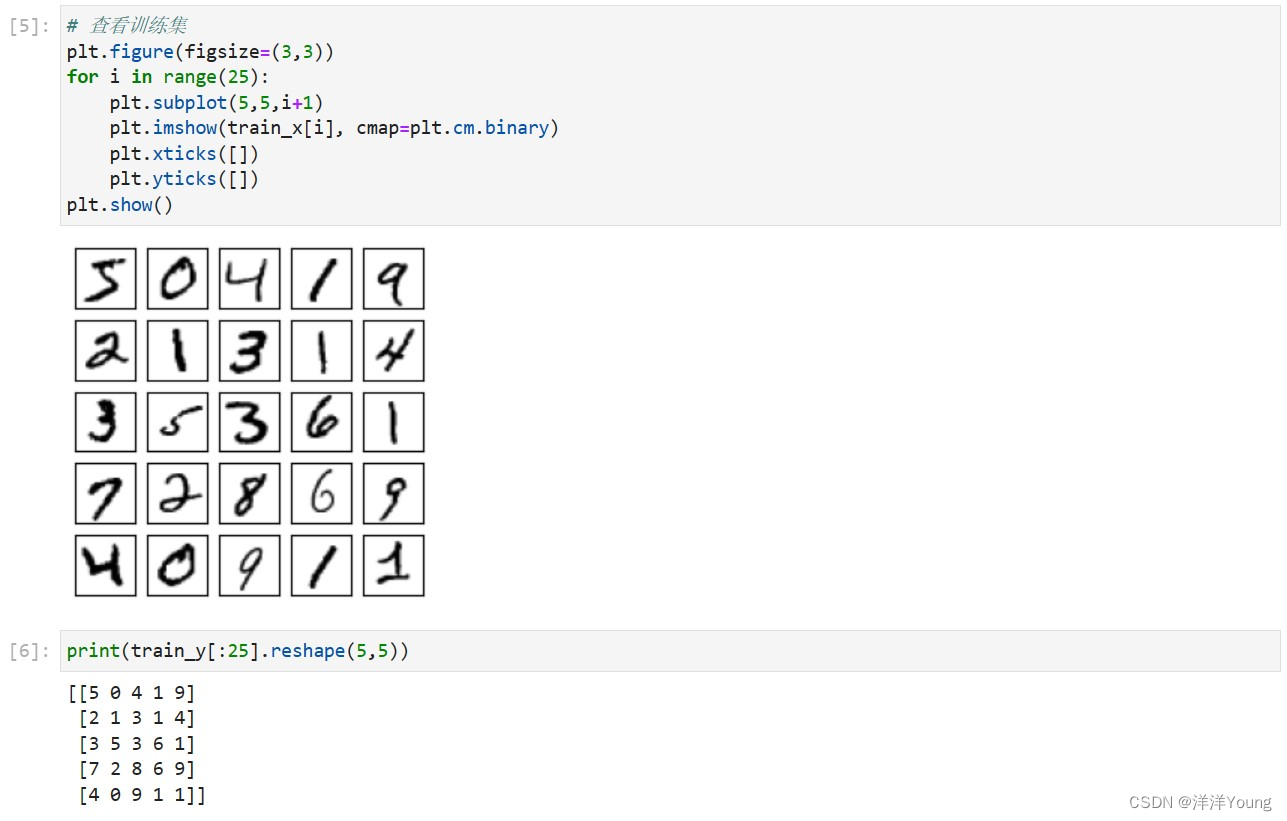
【卷积神经网络】MNIST 手写体识别
LeNet-5 是经典卷积神经网络之一,1998 年由 Yann LeCun 等人在论文 《Gradient-Based Learning Applied to Document Recognition》中提出。LeNet-5 网络使用了卷积层、池化层和全连接层,实现可以应用于手写体识别的卷积神经网络。TensorFlow 内置了 MNI…...
Ansible学习笔记2
Ansible是Python开发的自动化运维工具,集合了众多运维工具(Puppet、cfengine、chef、func、fabric)的优点,实现了批量系统配置,批量程序部署、批量运行命令等功能。 特点: 1)部署简单ÿ…...
80. 删除有序数组中的重复项 II
【中等题】 题目: 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额…...

CVE-2023-36874 Windows错误报告服务本地权限提升漏洞分析
CVE-2023-36874 Windows错误报告服务本地权限提升漏洞分析 漏洞简介 Windows错误报告服务在提交错误报告前会创建wermgr.exe进程,而攻击者使用特殊手法欺骗系统创建伪造的wermgr.exe进程,从而以system权限执行代码。 影响版本 Windows10 1507 * Wind…...
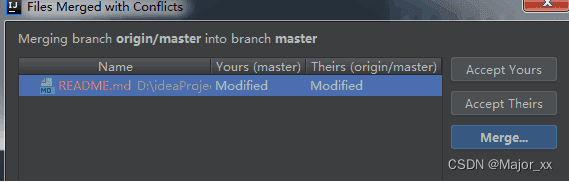
IDEA遇到 git pull 冲突的几种解决方法
1 忽略本地修改,强制拉取远程到本地 主要是项目中的文档目录,看的时候可能多了些标注,现在远程文档更新,本地的版本已无用,可以强拉 git fetch --all git reset --hard origin/dev git pull关于commit和pull的先后顺…...
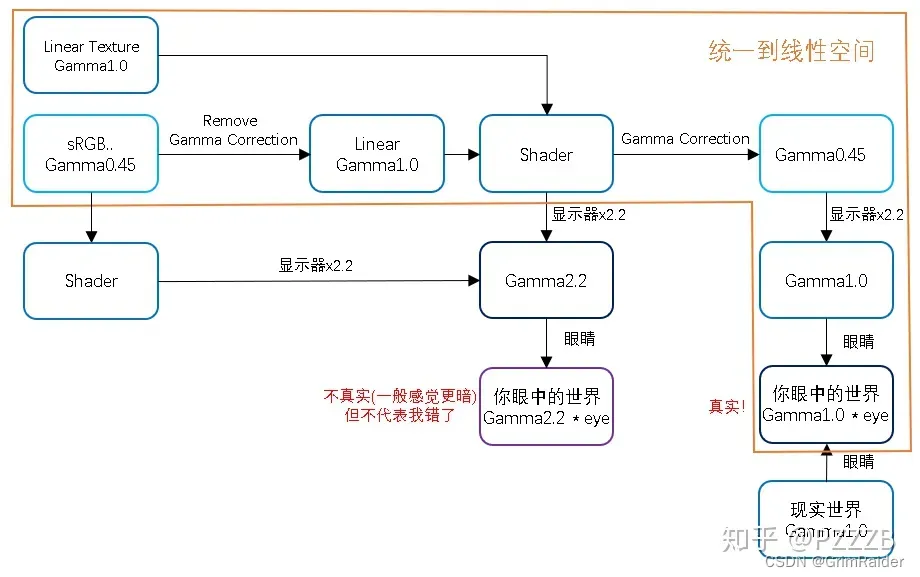
[Unity]UI和美术出图效果不一致
问题描述:美术使用PS在Gamma空间下设计的UI图,导入到Unity,因为Unity使用的是线性空间,导致半透明的UI效果和美术设计的不一致。 解决方案: (一)让美术在线性空间下工作 (二&…...

SpringBoot整合JPA和Hibernate框架
Springboot整合JPAHibernate框架【待完成】 随着MybatisPlus技术的发展,JPA和Hibernate技术已经逐步淘汰 JPA遵循了Hibernate框架规则,目前使用的不多 1、添加依赖 <!--jpa--> <dependency><groupId>org.springframework.boot</…...
,文件常用的方法)
Java中文件的创建(三种方式),文件常用的方法
文件的创建 方式1: new File(String pathName) 根据路径构建一个File对象方式2: new File(File parent,String child) 根据父目录文件子路径构建方式3: new File(String parent,String child) 根据父目录子路径构建 代码: //方…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
