二叉搜索树(C++)
二叉搜索树
- 概念
- 二叉搜索树的应用
- 二叉搜索树的实现
- K模型
- 基本结构和函数声明
- 接口实现
- ①find——查找关键码
- ②Insert——插入关键码
- ③Erase——删除关键码(==重点==)
- 时间复杂度
- 源码(整体)
- 非递归
- 递归
- KV模型
在使用C语言写数据结构阶段时,对二叉树进行了讲解。本节内容是对二叉树的深入探索,也是二叉树部分的收尾
概念
二叉搜索树也称二叉排序树(BST,Binary Search Tree):
- 空树
- 非空树(要具有以下性质)
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
注意: 二叉搜索树的key值互不相同
eg:下图就属于二叉搜索树
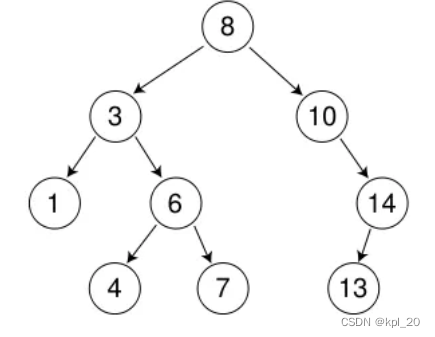
二叉搜索树的应用
-
K模型:即只有key作为关键码,结构中只需要存储key。关键码就是要搜索到的值
eg: 给一个单词word,判断该单词是否拼写正确?具体步骤:1. 以词库中所有单词为基础,每个单词都是key,构建一颗搜索二叉树2. 在二叉树中搜索该单词是否存在,存在则返回true,否则返回false -
KV模型:每一个关键码key,都有与之对应的value,即<Key, Value>的键值对
eg1: 英汉词典 - 就是中文与英文的对应关系。通过英文可以快速找到与其对应的中文,英文单词和与其对应的中文<word, chinese>就构成键值对。eg2: 统计单词次数,统计成功后,给定单词就可以找到单词出现得次数。单词与其出现次数就是<word, count>就构成一种键值对
二叉搜索树的实现
注意: 通过二叉搜索树的应用,了解到其有两个模型,接下来对这两个模型分别进行实现。因为两个模型的接口都相似,所以仅对一个模型的接口进行详细介绍。
K模型
K模型的实现分为递归和非递归两种,但是接口的实现逻辑是一样的。为了便于理解把基本结构和函数声明先附上,然后对接口进行讲解,最后在贴上完整的源码
基本结构和函数声明
//二叉树节点
//节点使用struct,默认public访问
template<class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public://默认构造BSTree():_root(nullptr){}//拷贝构造BSTree(const BSTree<K>& t);//赋值运算符重载BSTree<K>& operator=(BSTree<K> t);//析构函数~BSTree();//插入bool Insert(const K& key);//查找bool Find(const K& key);//删除bool Erase(const K& key);//中序遍历void InOrder();private:Node* _root;
};
接口实现
①find——查找关键码
功能:查找关键码是否在树中,是返回真,否则返回假。
原理:
- 从根开始比较,比根大则往右边查找,比根小往左边查找
- 最多查找高度次,走到nullptr,则这个值不存在
实现代码
- 非递归版本
template<class K>
bool BSTree<K>::Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;}}return false;
}
- 递归版本
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;}}return false;
}
②Insert——插入关键码
原理:
- 树为空,直接把要插入的节点赋值给root
- 树不为空,通过查找的思路,找到要插入的合适位置。插入成功返回true
注意:如果要插入的值和树中的值冲突,则返回false
实现代码
- 非递归版本
//插入
bool Insert(const K& key)
{if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key);if (parent->_key > key){parent->_left = cur;}else{parent->_right = cur;}return true;
}
- 递归版本
bool InsertR(const K& key)
{return _InsertR(_root, key);
}
bool _FindR(Node* root, const K& key)
{if (root == nullptr)return false;if (root->_key > key)return _FindR(root->_left, key);else if (root->_key < key)return _FindR(root->_right, key);elsereturn true;
}
③Erase——删除关键码(重点)
原理:
- 查找关键码是否在二叉搜索树中,不存在直接返回false
- 存在,则要分为四种情况
情况:
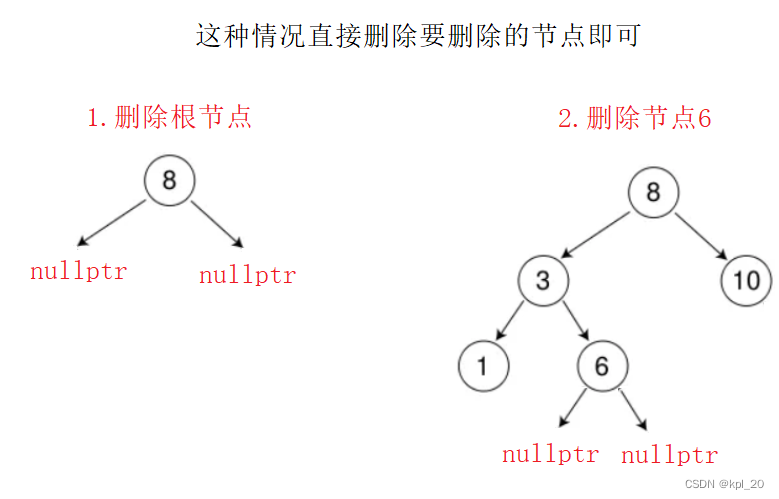
在考虑树的所有情况时,要把根节点的情况和普通情况,分离开来。哪怕最后根节点的情况和普通情况一样。(仅代表博主个人观点)
- 要删除的节点无孩子节点
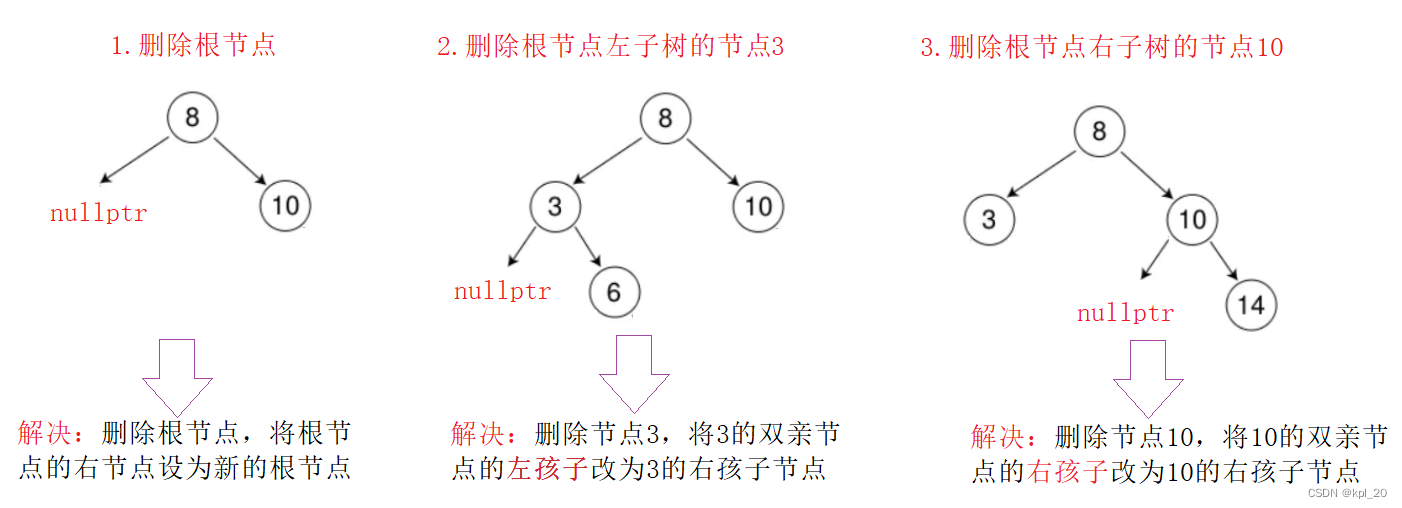
- 要删除的节点无左孩子节点
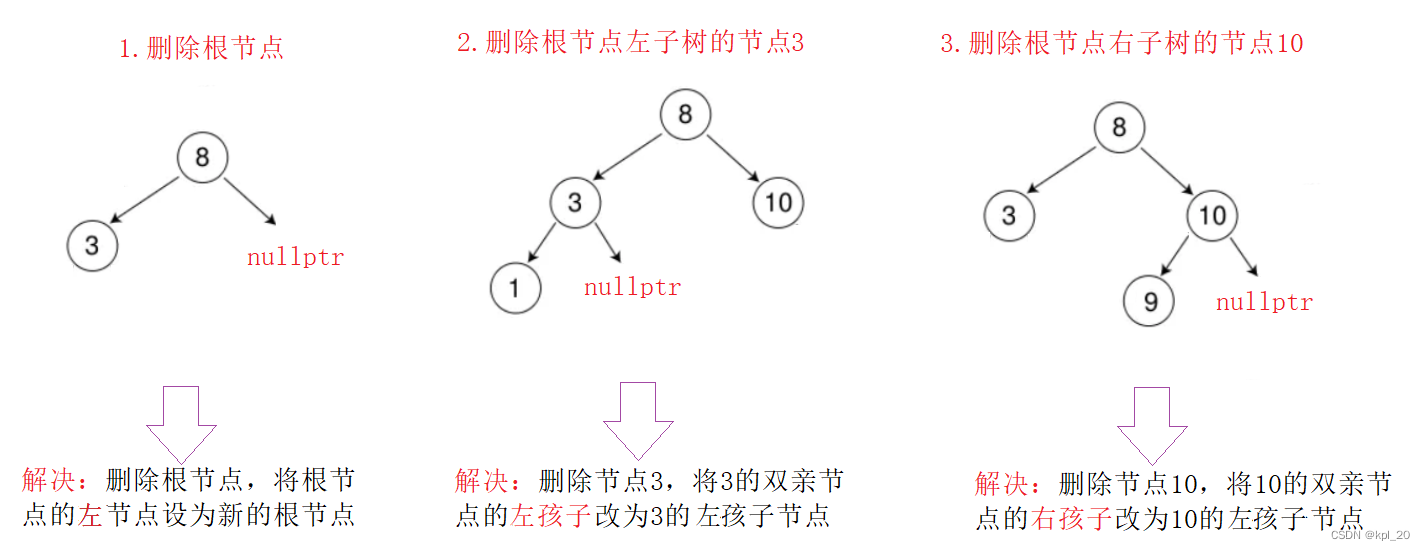
- 要删除的节点无右孩子节点
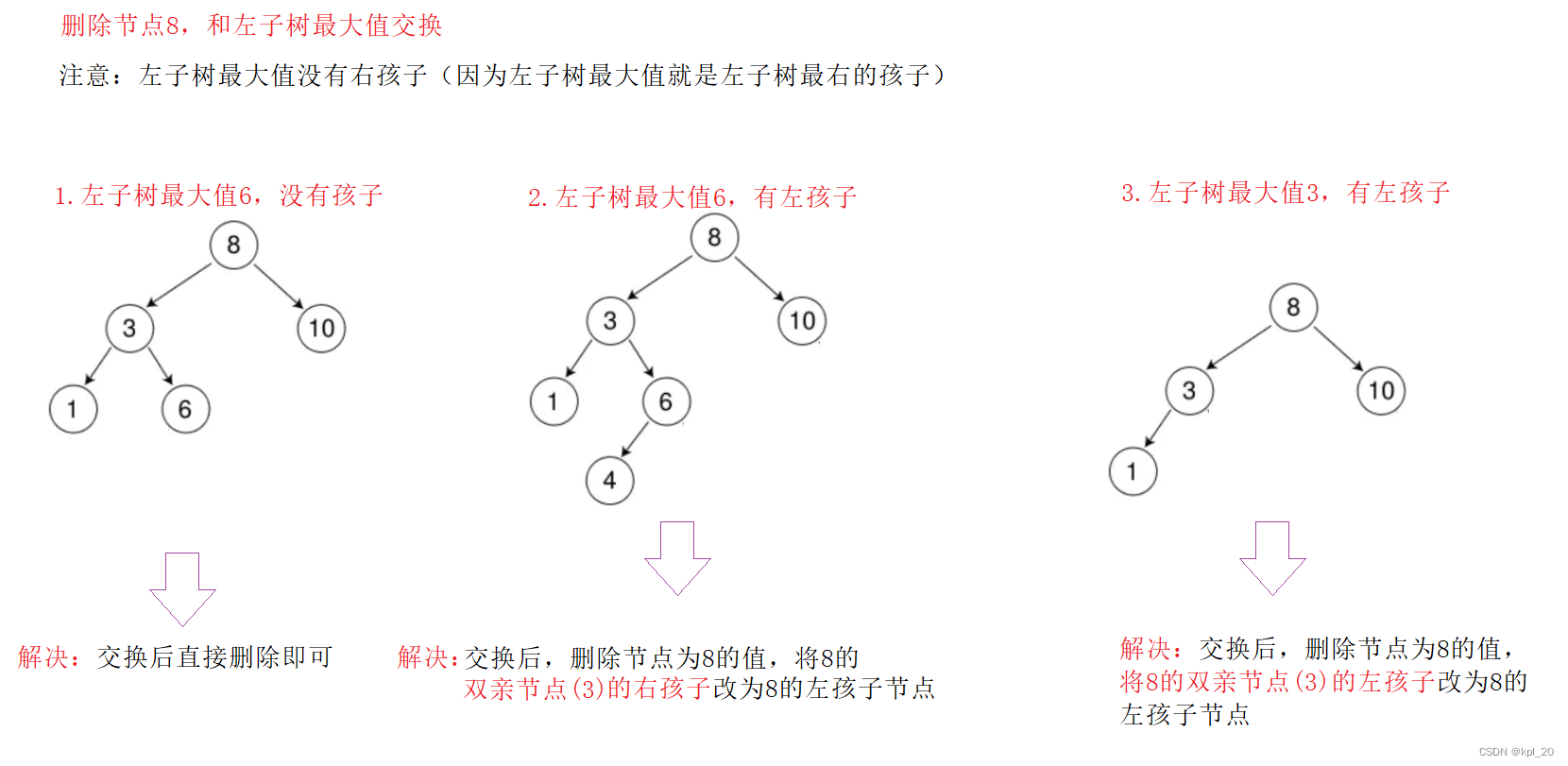
- 要删除的节点左右都不为空 (采用的方法 一 替换法)
替换法:找到删除节点左子树的最大值节点(leftMax),然后与删除节点交换,再删除现在的leftMax。(也可以找删除节点右子树的最小值节点(rightMin),原理相同)
实现代码
- 非递归版本
//删除
bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else //找到了要删除的值{//分情况//1.左为空if (cur->_left == nullptr){if (cur == _root)_root = cur->_right;else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}//2.右为空else if (cur->_right == nullptr){if (cur == _root)_root = cur->_left;else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}} //3.左右都不为空else{parent = cur;Node* leftMax = cur->_left;while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;}swap(cur->_key, leftMax->_key);if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;}cur = leftMax;}delete cur;cur = nullptr;return true;}}return false;
}
- 递归版本
//删除
bool EraseR(const K& key)
{return _EraseR(_root, key);
}bool _EraseR(Node*& root, const K& key)
{if (root == nullptr)return false;if (root->_key < key)return _EraseR(root->_right, key);else if (root->_key > key)return _EraseR(root->_left, key);else{Node* del = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;del = nullptr;return true;}
}
时间复杂度
二叉搜索树的操作时间复杂度:在O(logN)和O(N)之间。
画图解释时间复杂度:
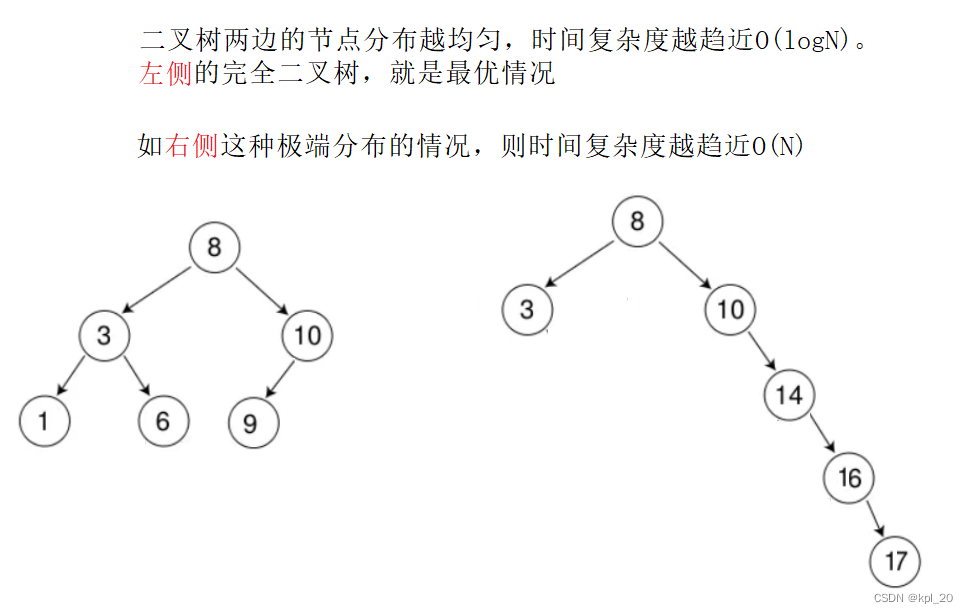
源码(整体)
非递归
//非递归
namespace key
{//二叉树节点//节点使用struct,默认public访问template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public://默认构造BSTree():_root(nullptr){}//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}//赋值运算符重载BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}//析构函数~BSTree(){Destroy(_root);}//插入bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key);if (parent->_key > key){parent->_left = cur;}else{parent->_right = cur;}return true;}//查找bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;}}return false;}//删除bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else //找到了要删除的值{//分情况//1.左为空if (cur->_left == nullptr){if (cur == _root)_root = cur->_right;else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}//2.右为空else if (cur->_right == nullptr){if (cur == _root)_root = cur->_left;else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}} //3.左右都不为空else{parent = cur;Node* leftMax = cur->_left;while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;}swap(cur->_key, leftMax->_key);if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;}cur = leftMax;}delete cur;cur = nullptr;return true;}}return false;}//中序遍历void InOrder(){_InOrder(_root);cout << endl;}private:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* copyRoot = new Node(root->_key);copyRoot->_left = Copy(root->_left);copyRoot->_right = Copy(root->_tight);return copyRoot;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root;};
}
递归
//递归
namespace keyR
{//二叉树节点//节点使用struct,默认public访问template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public://默认构造BSTree():_root(nullptr){}//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}//赋值运算符重载BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}//析构函数~BSTree(){Destroy(_root);}//插入bool InsertR(const K& key){return _InsertR(_root, key);}//查找bool FindR(const K& key){return _FindR(_root, key);}//删除bool EraseR(const K& key){return _EraseR(_root, key);}//中序遍历void InOrder(){_InOrder(_root);cout << endl;}private://在root添加引用很关键,要不然得是二级指针bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key > key)return _InsertR(root->_left, key);else if (root->_key < key)return _InsertR(root->_right, key);elsereturn false;}bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key)return _EraseR(root->_right, key);else if (root->_key > key)return _EraseR(root->_left, key);else{Node* del = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;del = nullptr;return true;}}bool _FindR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key > key)return _FindR(root->_left, key);else if (root->_key < key)return _FindR(root->_right, key);elsereturn true;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* copyRoot = new Node(root->_key);copyRoot->_left = CopyRoot(root->_left);copyRoot->_right = CopyRoot(root->_right);return copyRoot;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root;};
}
KV模型
直接贴出源码:
namespace key_value
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:BSTree():_root(nullptr){}BSTree(const BSTree<K, V>& t){_root = Copy(t._root);}BSTree<K, V>& operator=(BSTree<K, V> t){swap(_root, t._root);return *this;}~BSTree(){Destroy(_root);}void InOrder(){_InOrder(_root);cout << endl;}Node* FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key, const V& value){return _InsertR(_root, key, value);}bool EraseR(const K& key){return _EraseR(_root, key);}private:bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;if (root->_left == nullptr){//这个root的引用,非常好,root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);//删的值在左边return _EraseR(root->_left, key);}delete del;return true;}}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* copyRoot = new Node(root->_key, root->_value);copyRoot->_left = Copy(root->_left);copyRoot->_right = Copy(root->_right);return copyRoot;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}Node* _FindR(Node* root, const K& key){if (root == nullptr)return nullptr;if (root->_key > key){return _FindR(root->_left, key);}else if (root->_key < key){return _FindR(root->_right, key);}else{return root;}}bool _InsertR(Node*& root, const K& key, const V& value){if (root == nullptr){root = new Node(key, value);return true;}if (root->_key > key){return _InsertR(root->_left, key, value);}else if (root->_key < key){return _InsertR(root->_right, key, value);}else{return false;}}private:Node* _root;};}
相关文章:

二叉搜索树(C++)
二叉搜索树 概念二叉搜索树的应用二叉搜索树的实现K模型基本结构和函数声明接口实现①find——查找关键码②Insert——插入关键码③Erase——删除关键码(重点)时间复杂度 源码(整体)非递归递归 KV模型 在使用C语言写数据结构阶段时…...

软件架构知识点
常用软件架构模型分类(5种) 软件架构建模方法(模型4种) 架构师分类(微软4种) 系统架构设计师的角色特质(6种) 计算机系统组成图谱 嵌入式操作系统的特点(5个&#x…...

C语言日常刷题6
文章目录 题目答案与解析1234567 题目 1、以下对C语言函数的有关描述中,正确的有【多选】( ) A: 在C语言中,一个函数一般由两个部分组成,它们是函数首部和函数体 B: 函数的实参和形参可以是相同的名字 C: 在main()中定…...
微信小程序使用stomp.js实现STOMP传输协议的实时聊天
简介: uniapp开发的小程序中使用 本来使用websocket,后端同事使用了stomp协议,导致前端也需要对应修改。 如何使用 在static/js中新建stomp.js和websocket.js,然后在需要使用的页面引入监听代码发送代码即可 代码如下&#x…...

基于饥饿游戏算法优化的BP神经网络(预测应用) - 附代码
基于饥饿游戏算法优化的BP神经网络(预测应用) - 附代码 文章目录 基于饥饿游戏算法优化的BP神经网络(预测应用) - 附代码1.数据介绍2.饥饿游戏优化BP神经网络2.1 BP神经网络参数设置2.2 饥饿游戏算法应用 4.测试结果:5…...

[ 云计算 | AWS ] Java 应用中使用 Amazon S3 进行存储桶和对象操作完全指南
文章目录 一、前言二、所需 Maven 依赖三、先决必要的几个条件信息四、创建客户端连接五、Amazon S3 存储桶操作5.1. 创建桶5.2. 列出桶 六、Amazon S3 对象操作6.1. 上传对象6.2. 列出对象6.3. 下载对象6.4. 复制、重命名和移动对象6.5. 删除对象6.6. 删除多个对象 七、文末总…...

【Spring Boot】Spring Boot 配置 Hikari 数据库连接池
文章目录 前言配置 前言 数据库连接池是一个提高程序与数据库的连接的优化,连接池它主要作用是提高性能、节省资源、控制连接数、连接管理等操作; 程序中的线程池与之同理,都是为了优化、提高性能。 配置 spring:datasource:hikari:# 设置是…...

MR混合现实石油化工课堂情景实训教学演示
MR(混合现实)技术是一种结合了虚拟现实(VR)和增强现实(AR)优势的新型技术,在教育领域具有广阔的应用前景。在石油化工课堂中,MR混合现实情景实训教学的应用可以大大提高学生的学习效…...

php thinkphp 抖音支付,订单同步接口分享
1. 抖音支付 需要获取抖音小程序的AppID,AppSecret,需要配置回调地址,Token获取SALT 官方地址:支付,订单同步 以下干货仅针对于有一定开发基础的精英,0基础的止步。 public function DouyinPay($openId,$id,$body 抖音担保支付…...

excel功能区(ribbonx)编程笔记--2 button控件与checkbox控件
我们上一章简单先了解了ribbonx的基本内容,以及使用举例实现自己修改ribbox的内容,本章紧接上一章,先讲解一下ribbonx的button控件。 在功能区的按钮中,可以使用内置图像或提供自已的图像,可以指定大按钮或者更小的形式,添加少量的代码甚至可以同时提供标签。此外,可以利…...

JavaScript 知识点
立即执行函数 代码(function () {// ... })();创建函数的同时立即执行,没有绑定任何事件,也无需等待任何异步操作function () {} 是一个匿名函数,包围它的一对括号将其转换为一个表达式,紧跟其后的一对括号调用了这个函数。立即执…...

深入理解 JVM 之——动手编译 JDK
更好的阅读体验 \huge{\color{red}{更好的阅读体验}} 更好的阅读体验 本篇为深入理解 Java 虚拟机第一章的实战内容,推荐在学习前先掌握基础的 Linux 操作、编译原理基础以及扎实的 C/C 功底。 该系列的 GitHub 仓库:https://github.com/Doge2077/lear…...
[移动通讯]【Carrier Aggregation in LTE】【 Theory + Log analysis-1】
CA: Carrrier Aggregation PCC: Primary Component Carrier SCC: SCC Secondary Component Carrier 目录: 背景介绍 PCC & SCC 聚合方式 Precondition for CA 一 背景介绍 在没有CA 技术前,手机和基站以单子载波的方式,收发…...

Sui诚邀您参加KBW「首尔Web3之夜」
韩国区块链周(KBW)是由FACTBLOCK创办,Hashed联合主办的年度盛会。今年的KBW将于9月4–10日在韩国首尔举办。作为亚洲最具影响力的Web3行业盛会之一,KBW将汇聚业界优秀的参与者和先驱者,共同探讨区块链行业的未来。 Su…...

19.CSS雨云动画特效
效果 源码 <!DOCTYPE html> <html lang="en"> <head><meta charset="UTF-8"><title>Cloud & Rain Animation</title><link rel="stylesheet" href="style.css"> </head> <bo…...
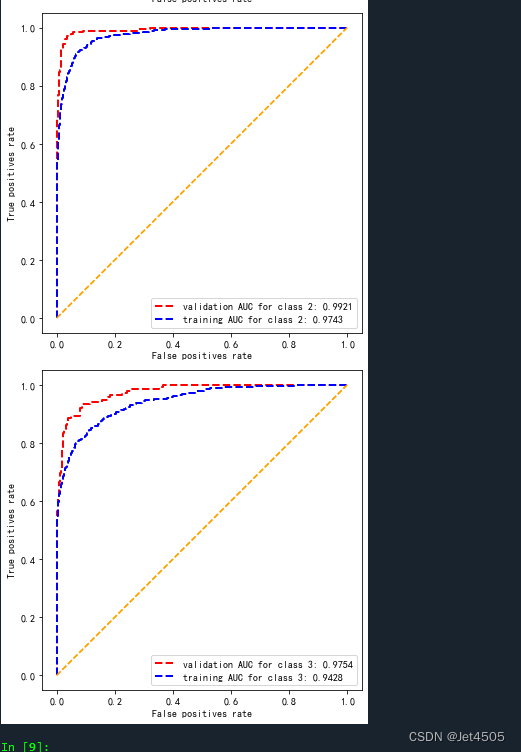
第61步 深度学习图像识别:多分类建模(TensorFlow)
基于WIN10的64位系统演示 一、写在前面 截至上期,我们一直都在做二分类的任务,无论是之前的机器学习任务,还是最近更新的图像分类任务。然而,在实际工作中,我们大概率需要进行多分类任务。例如肺部胸片可不仅仅能诊断…...

Spark 7:Spark SQL 函数定义
SparkSQL 定义UDF函数 方式1语法: udf对象 sparksession.udf.register(参数1,参数2,参数3) 参数1:UDF名称,可用于SQL风格 参数2:被注册成UDF的方法名 参数3:声明UDF的返回值类型 ud…...
ThinkPHP 文件上传 fileSystem 扩展的使用
ThinkPHP 文件上传 ThinkPHP 文件上传 扩展 filesystem一、安装 FileSystem 扩展二、认识 filesystem 配置文件 config/filesystem.php三、上传验证(涉及到验证器的知识点)四、文件上传demo ThinkPHP 文件上传 扩展 filesystem ThinkPHP 为我们 提供了 …...
液体神经网络LLN:通过动态信息流彻底改变人工智能
巴乌米克泰吉 一、说明 在在人工智能领域,神经网络已被证明是解决复杂问题的非常强大的工具。多年来,研究人员不断寻求创新方法来提高其性能并扩展其能力。其中一种方法是液体神经网络(LNN)的概念,这是一个利用动态计算…...

2023年的今天,PMP项目管理认证还值得考吗?
首先我肯定它值得考,PMP认证的教材和考纲都会随着项目管理工具和市场趋势而更新,不用担心会过时。 PMP项目管理认证是什么? 英文全称是Project Management Professional,中文全称叫做项目管理专业人士资格认证。它是由美国项目管…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...