国产自主可控C++工业软件可视化图形架构源码
关于国产自主代替的问题是当前热点,尤其是工业软件领域。
“一个功能强大的全自主C++跨平台图形可视化架构对开发自主可控工业基础软件至关重要!”
作为全球领先的C++工业基础图形可视化软件提供商,UCanCode软件有自己的思考,我们认为要提升国产自主工业软件开发能力的关键在于是否有一个开放的,功能强大的C++基础可视化图形架构,一个稳健,功能强大的图形可视化基础架构上面可以轻松构建各类工业组态监控、人机界面、CAD以及设计电力,能源,科学计算,电路仿真,电力仿真等基础工业软件。
为此,UCanCode花费了极大的精力将原来基于Windows的C++图形可视化架构Form++整体移植到Qt环境下,为国产自主工业软件开发提供一个稳健,功能强大,完全开放的基础架构。下面是VX++架构功能说明:
1、专业的制图模板:

2、类似于Visio的图元管理,总数超过3000个矢量图元,直接拖放支持:
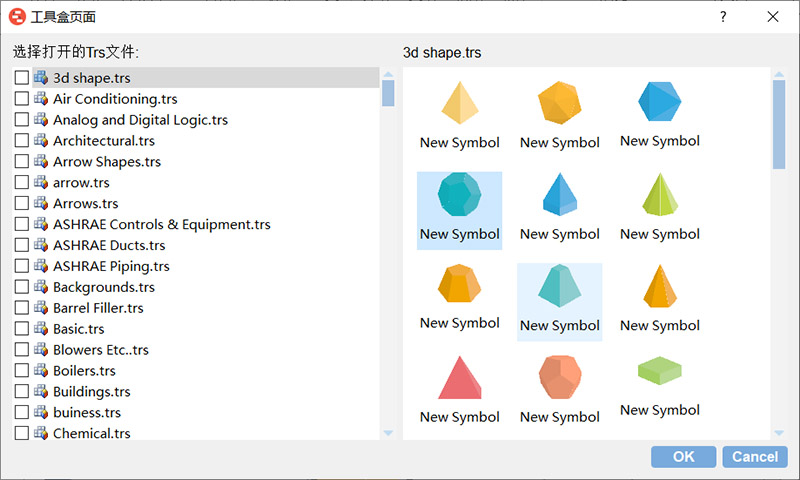
元件可以根据自己的需要任意增加和删除。
3、第三方SVG和CAD图纸导入功能,可以轻松扩展图元:

4、类似于Visio的所有矢量图编辑和排布功能:

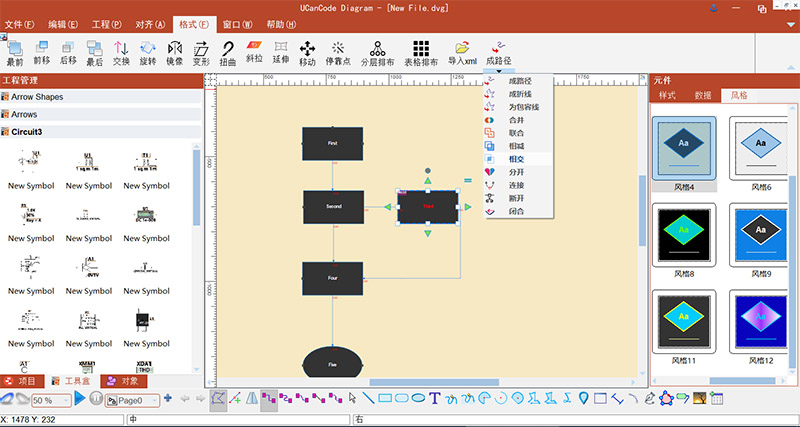
5、元件属性数据自定义:
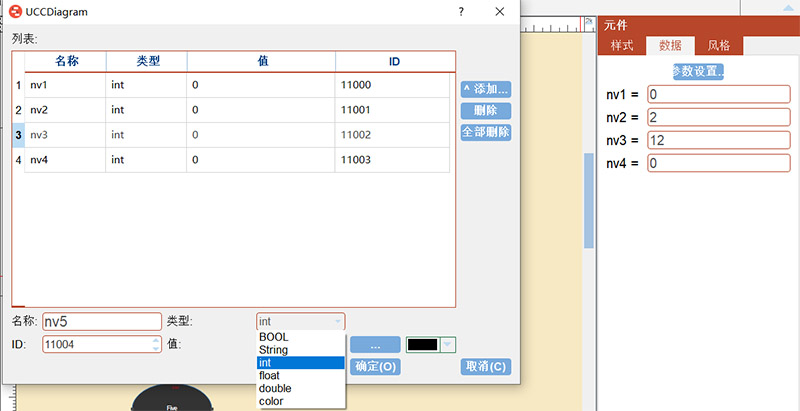
6、脚本自由控制:
每个元件的属性,动画等可以直接使用JavaScript自由控制:

7、图元与图元之间可以多种连接线自由连接:

8、连接线条自动绕开,当线条穿越画布上的图元的时候会自动绕开以避免覆盖,当线条和线条相交的时候会自动建立穿越标记。
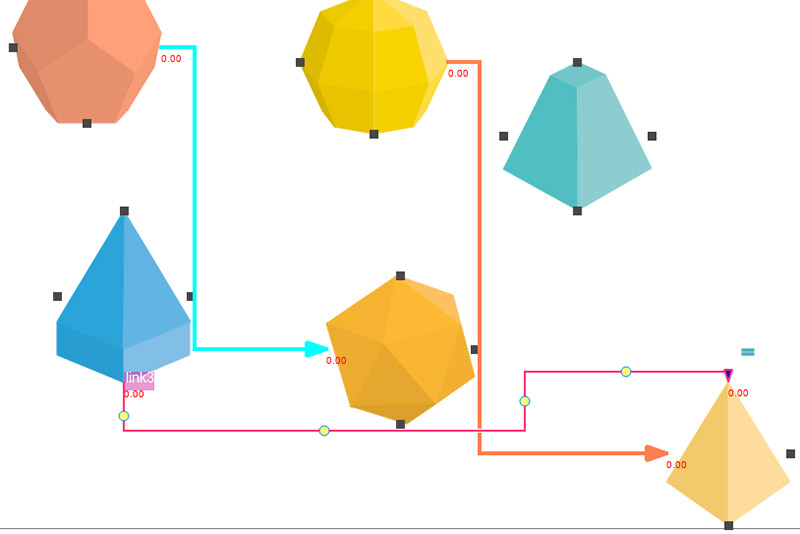
9、自动分层排布,自动分层排布能将复杂的图排布成规则的图:
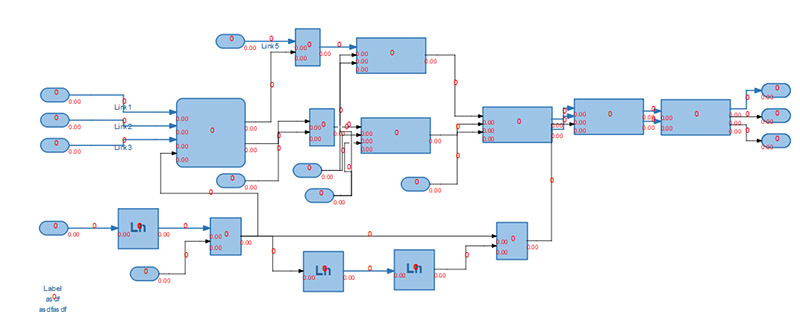
10、多页显示和管理,一个设计文件可以根据需要添加任意多个设计页面。
11、无极缩放和无极Undo/Redo支持。
12、集成IDE支持。可以在一个工程中添加制作多个画面。
13、SVG和Web的导出,支持导出html5+js编程。
14、组态和工业控制元件,包括仪表盘、实时、历史曲线等。
15、提供强大的Chart和表格元件。
16、条码元件支持。
17、自动捕捉、自动对齐功能。
18、高级多边形运算功能,求和、相并、相交、相减、打断、转换曲线等。
19、对多边形镜像、扭曲、变形、拉伸支持。
20、导出为PDF,打印等其他功能...
更加重要的是VX++所有源代码随正式版本100%提供,无任何保留!
VX++的所有核心代码均从UCanCode Form++移植而来,超过20年的客户验证,代码稳健、功能非常强大,是开发任何基础工业软件的必不可少的图形可视化架构。可根据需要扩展为新的工业软件产品。
包括各类仿真软件,建模软件,组态软件,工业控制软件,类CAD软件,UML软件等等。
希望能为国产自主可控贡献一些自己的力量!
了解更多,请访问:工控平台仿真平台C++源代码
下载免费试用版本,请访问:下载C++,源代码
相关文章:

国产自主可控C++工业软件可视化图形架构源码
关于国产自主代替的问题是当前热点,尤其是工业软件领域。 “一个功能强大的全自主C跨平台图形可视化架构对开发自主可控工业基础软件至关重要!” 作为全球领先的C工业基础图形可视化软件提供商,UCanCode软件有自己的思考,我们认…...

【linux命令讲解大全】022.网络管理工具和命令概述
文章目录 lsattr命令语法选项参数实例 nmcli补充说明语法选项OPTIONSOBJECT 实例 systemctl补充说明任务 旧指令 新指令 实例 开启防火墙22端口 从零学 python lsattr命令 用于查看文件的第二扩展文件系统属性。 语法 lsattr(选项)(参数) 选项 -E:可显示设备属…...

应急响应流程及思路
应急响应流程及思路 一:前言 对于还没有在项目中真正接触、参与过应急响应的同学来说,“应急响应”这四个字见的最多的就是建筑工地上的横幅 —— 人人懂应急,人人会响应。这里的应急响应和我们网络安全中的应急响应有着某种本质的相似&…...

网页自适应
自适应 那就要最好提前商量好 是全局自适应 或者是 局部自适应 一般网站页面纵向滚动条都是无法避免的 都是做横向适配也就是宽度 那就不能写死宽度像素 局部自适应 一般对父元素设置百分比就行 里面的子元素就设置固定像素、 比如一些登录 全局自适应 也就是要对每个元素…...

什么是Sui Kiosk,它可以做什么,如何赋能创作者?
创作者和IP持有者需要一些工具帮助他们在区块链上实现其商业模式。Sui Kiosk作为Sui上的一种原语可以满足这种需求,为创作者提供动态选项,使他们能够在任何交易场景中设置完成交易的条件。 本文将向您介绍为什么要在SuiFrens中使用Sui Kiosk,…...

【MySQL】mysql connect
目录 一、准备工作 1、创建mysql用户 2、删除用户 3、修改用户密码 3.1、自己改自己密码 3.2、root用户修改指定用户的密码 4、数据库的权限 4.1、给用户授权 4.2、回收权限 二、连接mysql client 1、安装mysql客户端库 2、验证是否引入成功 三、 mysql接口 1、初…...
基于 vue2 发布 npm包
背景:组件化开发需要,走了一遍发布npm包的过程,采用很简单的模式实现包的发布流程,记录如下。 项目参考:基于vue的时间播放器组件,并发布到npm_timeplay.js_xmy_wh的博客-CSDN博客 1、项目初始化 首先&a…...

基于Axios完成前后端分离项目数据交互
一、安装Axios npm i axios -S 封装一个请求工具:request.js import axios from axios// 创建可一个新的axios对象 const request axios.create({baseURL: http://localhost:9090, // 后端的接口地址 ip:porttimeout: 30000 })// request 拦截器 // 可以自请求…...

时序预测 | MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比
时序预测 | MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比 目录 时序预测 | MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比效果一览基本描述程序设计参考资料 效果一览 基本描述 MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比。 1.Matlab实现PSO-BiLSTM和BiLSTM…...
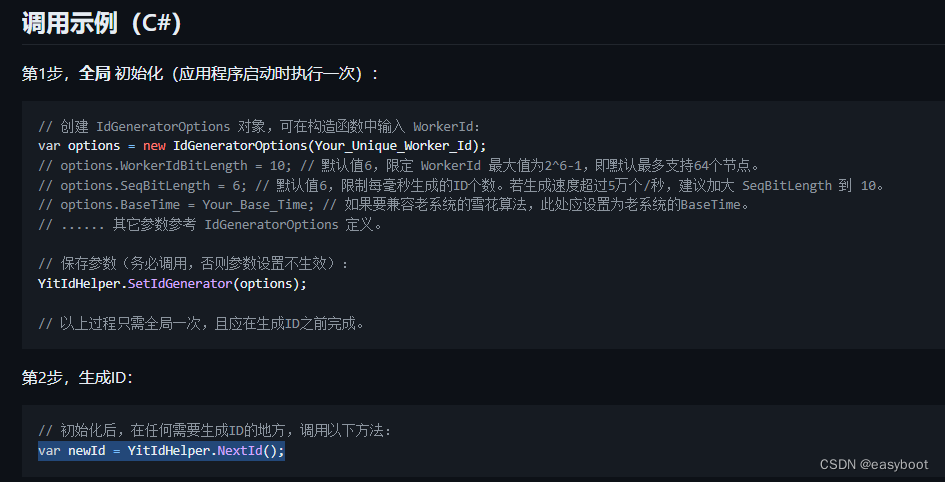
C# 生成唯一ID
1.首先通过nuget安装yitter.idgenerator 下面的三行代码搞定...

python怎么提取视频中的音频
目录 操作步骤 1. 安装MoviePy库: 2. 导入MoviePy库和所需的模块: 3. 提取音频: 可能遇到的问题 1. 编解码器支持: 2. 依赖项安装: 3. 文件路径问题: 4. 内存消耗: 5. 输出文件大小&a…...

学习设计模式之建造者模式,但是宝可梦
前言 作者在准备秋招中,学习设计模式,做点小笔记,用宝可梦为场景举例,有错误欢迎指出。 建造者模式 建造者模式是一种创建型模式,主要针对于某一个类有特别繁杂的属性,并且这些属性中有部分不是必须的。…...

数学建模:变异系数法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 变异系数法 变异系数法的设计原理是: 若某项指标的数值差异较大,能明确区分开各被评价对象,说明该指标的分辨信息丰富,因而应给该指标以较大的权重…...
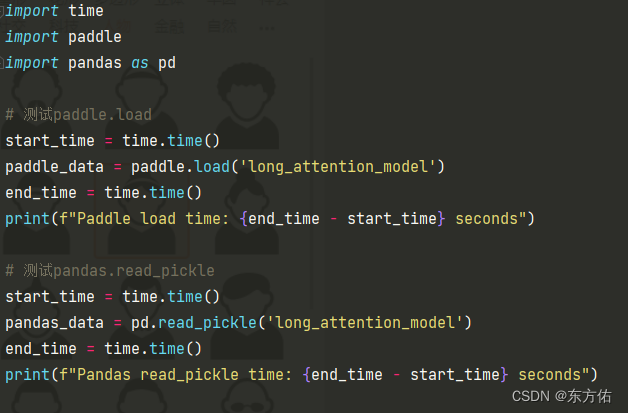
paddle.load与pandas.read_pickle的速度对比(分别在有gpu 何无gpu 对比)
有GPU 平台 测试通用代码 import time import paddle import pandas as pd# 测试paddle.load start_time time.time() paddle_data paddle.load(long_attention_model) end_time time.time() print(f"Paddle load time: {end_time - start_time} seconds")# 测试…...
探讨uniapp的路由与页面栈及参数传递问题
1首先引入页面栈 框架以栈的形式管理当前所有页面, 当发生路由切换的时候,页面栈的表现如下: 页面的路由操作无非:初始化、打开新页面、页面重定向、页面返回、tab切换、重加载。 2页面路由 uni-app 有两种页面路由跳转方式&am…...

字节一面:你能讲一下跨域吗
前言 最近博主在字节面试中遇到这样一个面试题,这个问题也是前端面试的高频问题,作为一名前端开发工程师,我们日常开发中与后端联调时一定会遇到跨域的问题,只有处理好了跨域才能够与后端交互完成需求,所以深入学习跨域…...

leetcode 563.二叉树的坡度
⭐️ 题目描述 🌟 leetcode链接:https://leetcode.cn/problems/binary-tree-tilt/description/ 代码: class Solution { public:int childFind(TreeNode* root , int& sumTile) {if (root nullptr) {return 0; // 空树坡度为0}int l…...
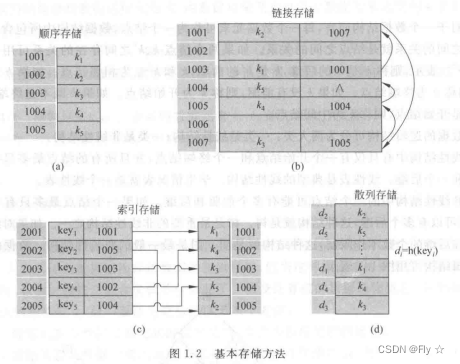
【第1章 数据结构概述】
目录 一. 基本概念 1. 数据、数据元素、数据对象 2. 数据结构 二. 数据结构的分类 1. 数据的逻辑结构可分为两大类:a. 线性结构;b. 非线性结构 2. 数据的存储结构取决于四种基本的存储方法:顺序存储、链接存储、索引存储、散列存储 3. …...

【附安装包】MyEclipse2019安装教程
软件下载 软件:MyEclipse版本:2019语言:简体中文大小:1.86G安装环境:Win11/Win10/Win8/Win7硬件要求:CPU2.5GHz 内存4G(或更高)下载通道①百度网盘丨下载链接:https://pan.baidu.co…...

poi-tl设置图片(通过word模板替换关键字,然后转pdf文件并下载)
选中图片右击 选择设置图片格式 例如word模板 maven依赖 <!-- java 读取word文件里面的加颜色的字体 转pdf 使用 --><dependency><groupId> e-iceblue </groupId><artifactId>spire.doc.free</artifactId><version>3.9.0</ver…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
