(动态规划) 剑指 Offer 60. n个骰子的点数 ——【Leetcode每日一题】
❓ 剑指 Offer 60. n个骰子的点数
难度:中等
把 n 个骰子扔在地上,所有骰子朝上一面的点数之和为 s 。输入 n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
示例 1:
输入: 1
输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
示例 2:
输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
限制:
1 <= n <= 11
💡思路:动态规划
使用一个二维数组 dp 存储点数出现的次数,其中 dp[i][j] 表示前 i 个骰子产生点数 j 的次数。
只看第 n 枚骰子,它的点数可能为 1, 2, 3, ... , 6 ,因此投掷完 n 枚骰子后点数 j 出现的次数,可以由投掷完 n−1 枚骰子后,对应点数 j−1, j−2, j−3, ..., j−6 出现的次数之和转化过来。
for (第n枚骰子的点数 k = 1; k <= 6; k++) {dp[n][j] += dp[n-1][j - k]
}
写成数学公式是这样的:
d p [ n ] [ j ] = ∑ i = 1 6 d p [ n − 1 ] [ j − k ] dp[n][j]=\sum_{i=1}^6dp[n-1][j-k] dp[n][j]=i=1∑6dp[n−1][j−k]
n 表示阶段,j 表示投掷完 n 枚骰子后的点数和,k 表示第 n 枚骰子会出现的六个点数。
⭐️ 空间优化: 旋转数组
观察发现每个阶段的状态都只和它前一阶段的状态有关,因此我们不需要用额外的一维来保存所有阶段。
- 用两个一维数组交替变换存储。
🍁代码:(C++、Java)
C++
class Solution {
public:vector<double> dicesProbability(int n) {int maxsum = n * 6;vector<vector<long long>> dp(n + 1, vector<long long>(maxsum + 1));for(int i = 1; i <= 6; i++){dp[1][i] = 1;}for(int i = 2; i <= n; i++){for(int j = i; j <= i * 6; j++){for(int k = 1; k <= 6 && k <= j; k++){dp[i][j] += dp[i - 1][j - k];}}}long long totalnum = pow(6, n);vector<double> ans(n * 5 + 1);for(int i = n; i <= maxsum; i++){ans[i - n] = (double)dp[n][i] / totalnum;}return ans;}
};
⭐️ 空间优化: 旋转数组
C++
class Solution {
public:vector<double> dicesProbability(int n) {int maxsum = n * 6;vector<vector<long long>> dp(2, vector<long long>(maxsum + 1));for(int i = 1; i <= 6; i++){dp[0][i] = 1;}int flag = 1; //旋转标记for(int i = 2; i <= n; i++, flag = 1 - flag){for(int j = 0; j <= i * 6; j++){dp[flag][j] = 0; //旋转数组清零}for(int j = i; j <= i * 6; j++){for(int k = 1; k <= 6 && k < j; k++){dp[flag][j] += dp[1 - flag][j - k];}}}long long totalnum = pow(6, n);vector<double> ans(n * 5 + 1);for(int i = n; i <= maxsum; i++){ans[i - n] = (double)dp[1 - flag][i] / totalnum;}return ans;}
};
Java
class Solution {public double[] dicesProbability(int n) {int maxsum = n * 6;long[][] dp = new long[2][maxsum + 1];for(int i = 1; i <= 6; i++){dp[0][i] = 1;}int flag = 1; //旋转标记for(int i = 2; i <= n; i++, flag = 1 - flag){for(int j = 0; j <= i * 6; j++){dp[flag][j] = 0; //旋转数组清零}for(int j = i; j <= i * 6; j++){for(int k = 1; k <= 6 && k < j; k++){dp[flag][j] += dp[1 - flag][j - k];}}}double totalnum = Math.pow(6, n);double[] ans = new double[n * 5 + 1];for(int i = n; i <= maxsum; i++){ans[i - n] = dp[1 - flag][i] / totalnum;}return ans;}
}
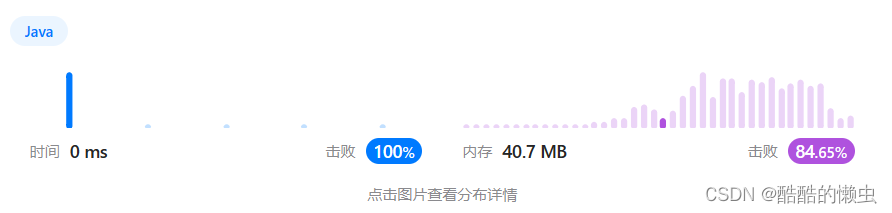
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2), 状态转移循环
n−1轮;每轮中,当i=2,3,...,n时,对应循环数量分别为6×6,11×6,...,[5(n−1)+1]×6;因此总体复杂度为 O ( ( n − 1 ) × 6 + [ 5 ( n − 1 ) + 1 ] 2 × 6 ) O((n−1)×\frac{6+[5(n-1)+1]}2×6) O((n−1)×26+[5(n−1)+1]×6),即等价于 O ( n 2 ) O(n^2) O(n2)。 - 空间复杂度: O ( n ) O(n) O(n),
dp数组需要2*n*6的空间,所以 O ( 2 ∗ n ∗ 6 ) = O ( n ) O(2*n*6) = O(n) O(2∗n∗6)=O(n)。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

(动态规划) 剑指 Offer 60. n个骰子的点数 ——【Leetcode每日一题】
❓ 剑指 Offer 60. n个骰子的点数 难度:中等 把 n 个骰子扔在地上,所有骰子朝上一面的点数之和为 s 。输入 n,打印出s的所有可能的值出现的概率。 你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点…...
ArrayList与顺序表
文章目录 一. 顺序表是什么二. ArrayList是什么三. ArrayList的构造方法四. ArrayList的常见方法4.1 add()4.2 size()4.3 remove()4.4 get()4.5 set()4.6 contains()4.7 lastIndexOf()和 indexOf()4.8 subList()4.9 clear() 以上就是ArrayList的常见方法!…...

【【萌新的STM32-22中断概念的简单补充】】
萌新的STM32学习22-中断概念的简单补充 我们需要注意的是这句话 从上面可以看出,STM32F1 供给 IO 口使用的中断线只有 16 个,但是 STM32F1 的 IO 口却远远不止 16 个,所以 STM32 把 GPIO 管脚 GPIOx.0~GPIOx.15(xA,B,C,D,E,F,G)分别对应中断…...

Java 中数据结构HashMap的用法
Java HashMap HashMap 是一个散列表,它存储的内容是键值对(key-value)映射。 HashMap 实现了 Map 接口,根据键的 HashCode 值存储数据,具有很快的访问速度,最多允许一条记录的键为 null,不支持线程同步。 HashMap 是…...
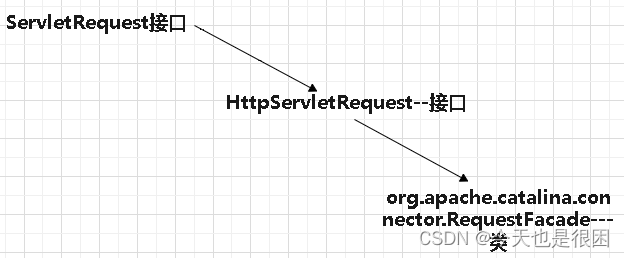
Request对象和response对象
一、概念 request对象和response对象是通过Servlet容器(如Tomcat)自动创建并传递给Servlet的。 Servlet容器负责接收客户端的请求,并将请求信息封装到request对象中,然后将request对象传 递给相应的Servlet进行处理。类似地&…...

设计模式之桥接模式
文章目录 一、介绍二、案例1. 组件抽象化2. 桥梁抽象化 一、介绍 桥接模式,属于结构型设计模式。通过提供抽象与实现之间的桥接结构,把抽象化与实现化解耦,使得二者可以独立变化。 《Head First 设计模式》: 将抽象和实现放在两…...
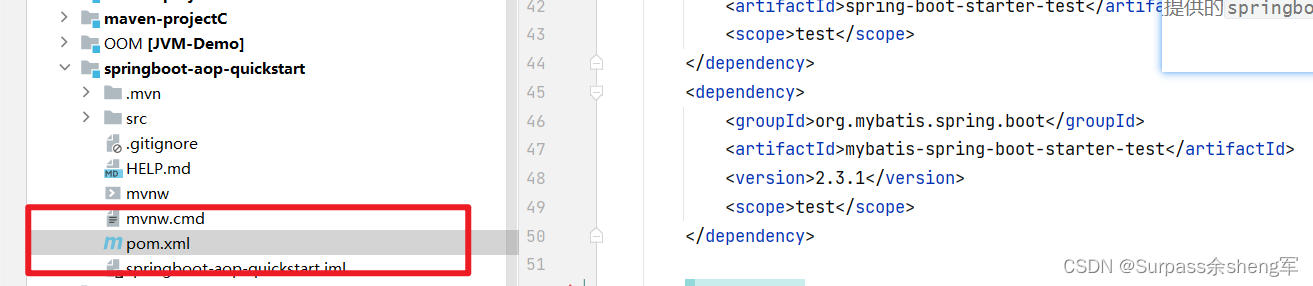
pom.xml配置文件失效,显示已忽略的pom.xml --- 解决方案
现象: 在 Maven 创建模块Moudle时,由于开始没有正确创建好,所以把它删掉了,然后接着又创建了与一个与之前被删除的Moudle同名的Moudle时,出现了 Ignore pom.xml,并且新创建的 Module 的 pom.xml配置文件失效…...

文本编辑器Vim常用操作和技巧
文章目录 1. Vim常用操作1.1 Vim简介1.2 Vim工作模式1.3 插入命令1.4 定位命令1.5 删除命令1.6 复制和剪切命令1.7 替换和取消命令1.8 搜索和搜索替换命令1.9 保存和退出命令 2. Vim使用技巧 1. Vim常用操作 1.1 Vim简介 Vim是一个功能强大的全屏幕文本编辑器,是L…...
【算法系列篇】位运算
文章目录 前言什么是位运算算法1.判断字符是否唯一1.1 题目要求1.2 做题思路1.3 Java代码实现 2. 丢失的数字2.1 题目要求2.2 做题思路2.3 Java代码实现 3. 两数之和3.1 题目要求3.2 做题思路3.3 Java代码实现 4. 只出现一次的数字4.1 题目要求4.2 做题思路4.3 Java代码实现 5.…...

机器学习的测试和验证(Machine Learning 研习之五)
关于 Machine Learning 研习之三、四,可到秋码记录上浏览。 测试和验证 了解模型对新案例的推广效果的唯一方法是在新案例上进行实际尝试。 一种方法是将模型投入生产并监控其性能。 这很有效,但如果你的模型非常糟糕,你的用户会抱怨——这…...

RNN循环神经网络
目录 一、卷积核与循环核 二、循环核 1.循环核引入 2.循环核:循环核按时间步展开。 3.循环计算层:向输出方向生长。 4.TF描述循环计算层 三、TF描述循环计算 四、RNN使用案例 1.数据集准备 2.Sequential中RNN 3.存储模型,acc和lose…...
安防视频监控/视频集中存储/云存储平台EasyCVR无法播放HLS协议该如何解决?
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。音视频流媒体视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、…...

Docker技术--Docker的安装
1..Docker的安装方式介绍 Docker官方提供了三种方式可以实现Docker环境的安装。分别为:Script、yum、rpm。在实际的环境中建议使用yum或者是rpm。 2..Docker的yum安装 # 1.下载docker wget https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo -O /etc/yum.re…...
客户案例|MemFire Cloud助推应急管理业务,打造百万级数据可视化大屏
「导语」 硬石科技,成立于2018年,总部位于武汉,是一家专注于应急管理行业和物联感知预警算法模型的技术核心的物联网产品和解决方案提供商。硬石科技作为一家高新技术企业,持有6项发明专利,拥有100余项各类平台认证和资…...
蒲公英路由器如何设置远程打印?
现如今,打印机已经是企业日常办公中必不可少的设备,无论何时何地,总有需要用到打印的地方,包括资料文件、统计报表等等。 但若人在外地或分公司,有文件急需通过总部的打印机进行打印时,由于不在同一物理网络…...
国产自主可控C++工业软件可视化图形架构源码
关于国产自主代替的问题是当前热点,尤其是工业软件领域。 “一个功能强大的全自主C跨平台图形可视化架构对开发自主可控工业基础软件至关重要!” 作为全球领先的C工业基础图形可视化软件提供商,UCanCode软件有自己的思考,我们认…...

【linux命令讲解大全】022.网络管理工具和命令概述
文章目录 lsattr命令语法选项参数实例 nmcli补充说明语法选项OPTIONSOBJECT 实例 systemctl补充说明任务 旧指令 新指令 实例 开启防火墙22端口 从零学 python lsattr命令 用于查看文件的第二扩展文件系统属性。 语法 lsattr(选项)(参数) 选项 -E:可显示设备属…...

应急响应流程及思路
应急响应流程及思路 一:前言 对于还没有在项目中真正接触、参与过应急响应的同学来说,“应急响应”这四个字见的最多的就是建筑工地上的横幅 —— 人人懂应急,人人会响应。这里的应急响应和我们网络安全中的应急响应有着某种本质的相似&…...

网页自适应
自适应 那就要最好提前商量好 是全局自适应 或者是 局部自适应 一般网站页面纵向滚动条都是无法避免的 都是做横向适配也就是宽度 那就不能写死宽度像素 局部自适应 一般对父元素设置百分比就行 里面的子元素就设置固定像素、 比如一些登录 全局自适应 也就是要对每个元素…...

什么是Sui Kiosk,它可以做什么,如何赋能创作者?
创作者和IP持有者需要一些工具帮助他们在区块链上实现其商业模式。Sui Kiosk作为Sui上的一种原语可以满足这种需求,为创作者提供动态选项,使他们能够在任何交易场景中设置完成交易的条件。 本文将向您介绍为什么要在SuiFrens中使用Sui Kiosk,…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
