【算法系列篇】位运算

文章目录
- 前言
- 什么是位运算算法
- 1.判断字符是否唯一
- 1.1 题目要求
- 1.2 做题思路
- 1.3 Java代码实现
- 2. 丢失的数字
- 2.1 题目要求
- 2.2 做题思路
- 2.3 Java代码实现
- 3. 两数之和
- 3.1 题目要求
- 3.2 做题思路
- 3.3 Java代码实现
- 4. 只出现一次的数字
- 4.1 题目要求
- 4.2 做题思路
- 4.3 Java代码实现
- 5. 消失的两个数字
- 5.1 题目要求
- 5.2 做题思路
- 5.3 Java代码实现
- 总结
前言
位操作符想必大家都知道吧,&——按位与,|——按位或,^——按位异或,~——按位取法,位操作主要是用来操作二进制数的,就是因为它操作的是二进制,所以它的速度非常的快,那么既然他的速度很快,我们是否可以用位运算来解决一些实际问题呢?当然是可以的,这篇文章我将为大家分享如何使用位运算这种算法来解决一些问题。
什么是位运算算法
位运算算法是一组基于二进制位的操作符和操作方法的算法,用于在计算机中对二进制数字进行快速和高效的操作。位运算算法可以在二进制位级别上进行操作,包括位与(AND)、位或(OR)、位异或(XOR)、位取反(NOT)以及移位操作(左移和右移)等。
- 按位与(&):只有当两个比特位都为1的时候结果才为1,否则为0
- 按位或(|):两个比特位中有一个1,结果就为1
- 按位异或(^):两个比特位相同为0,相异为1
- 按位取反(~):除符号位之外,其它的比特位取反,为0结果为1,为1结果为0
位运算算法常用于以下情况:
- 位操作:可以通过位与、位或、位异或等运算符来对二进制数字的每一位进行操作,实现快速的位级别操作。
- 位掩码:可以使用位运算来创建和操作掩码,掩码经常用于标志位、权限控制和位字段的操作。
- 整数运算优化:位运算算法可以实现某些整数运算的高效实现,如乘以2的幂次方、除以2的幂次方、判断奇偶性等。
- 位图算法:位运算常用于位图算法,其中每个二进制位表示集合中的一个元素,可以进行高效的集合操作,如并集、交集、差集等。
- 压缩算法:位运算可以在压缩算法中起到重要的作用,用于压缩和解压缩数据,常见的例子包括哈夫曼编码和算术编码。
位运算算法通常具有高效性、简洁性和可移植性的特点,可以提供快速的底层操作,特别适合某些特定的问题和应用领域。在编写低级别的系统程序、嵌入式系统、网络协议和算法优化等方面,位运算算法发挥着重要的作用。
1.判断字符是否唯一
https://leetcode.cn/problems/is-unique-lcci/
1.1 题目要求
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
示例 1:
输入: s = "leetcode"
输出: false
示例 2:
输入: s = "abc"
输出: true
限制:
- 0 <= len(s) <= 100
- s[i]仅包含小写字母
- 如果你不使用额外的数据结构,会很加分。
class Solution {public boolean isUnique(String astr) {}
}
1.2 做题思路
通常判断唯一性的时候,我们首先想到的是哈希表,但是这里限制我们不适用额外的数据结构,我们虽然可以使用数组来模拟哈希表,但这都不是最优解,这道题最优的解法就是使用位图的思想。为什么会选择使用位图呢?因为题目中说明了:字符串中只包含小写字母,也就是无重复字符的字符串的长度最长为26,而一个整型0有4个字节,32个比特位,并且二进制的0和1则恰好可以标志某一字符有或者没有。
那么如何使用位图的思想来解决这个问题呢?我们可以将每一个字符所代表的ASCII码值来表示它在32个比特位中的位置,用循环来遍历字符串中的每一个字符,如果该字符在32个比特位中的对应位置是0的话,则用 | 运算,将该位置变为1,如果该位置为 1 的话,则说明出现了重复的字符。
1.3 Java代码实现
class Solution {public boolean isUnique(String astr) {//鸽巢原理,当字符串长度大于26的时候一定会有重复的字符if(astr.length() > 26) return fasle; int tmp = 0; //tmp 代表32位比特位的位图for(int i = 0; i < astr.length(); i++) {char ch = astr.charAt(i);if(((tmp >> (ch - 'a')) & 1) == 1) return false;else tmp = tmp | (1 << (ch - 'a'));}return true;}
}
2. 丢失的数字
https://leetcode.cn/problems/missing-number/
2.1 题目要求
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums = [3,0,1]
输出:2
解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,
因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1]
输出:2
解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,
因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1]
输出:8
解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,
因为它没有出现在 nums 中。
示例 4:
输入:nums = [0]
输出:1
解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,
因为它没有出现在 nums 中。
提示:
- n == nums.length
- 1 <= n <= 104
- 0 <= nums[i] <= n
- nums 中的所有数字都 独一无二
class Solution {public int missingNumber(int[] nums) {}
}
2.2 做题思路
这道题目的意思就是,原本数组中的元素应该是[0,数组长度],但是数组中缺少了一个数字,我们需要找到这个缺失的数字。这个题有很多种解法:
- 哈希表。
- 高斯求和。将原本数组中的元素的和减去现有数组所有元素的和就得到缺失的那个数字
- 排序。将数组进行排序,然后遍历数组找到缺失的那个数字
- 位运算
能用位运算解决就尽量用位运算来解决,因为位运算的速度非常快,那么这道题如何使用位运算来解决呢?在这之前,我们需要知道,^ 操作,当两个相同的数字进行异或操作的时候结果为0,那么我们可以将原本数组中元素和现有数组中的元素都进行异或操作,相同的两个数异或结果为0,到最后异或的结果就是我们要找的那个缺失的数字。
2.3 Java代码实现
class Solution {public int missingNumber(int[] nums) {int ret = 0;for(int n : nums) ret ^= n;for(int i = 0; i <= nums.length; i++) ret ^= i;return ret;}
}
3. 两数之和
https://leetcode.cn/problems/sum-of-two-integers/
3.1 题目要求
给你两个整数 a 和 b ,不使用 运算符 + 和 - ,计算并返回两整数之和。
示例 1:
输入:a = 1, b = 2
输出:3
示例 2:
输入:a = 2, b = 3
输出:5
提示:
- -1000 <= a, b <= 1000
class Solution {public int getSum(int a, int b) {}
}
3.2 做题思路
两数之和,大家一看到这个题目可能就会觉得很简单,直接 return a + b; 不就行了吗?但是仔细看题目,这道题不允许使用运算符 + 和 -,那么如何在不使用运算符的情况下实现两数之和呢?位运算,通过位运算就可以在不适用运算符的情况下实现两数之和的运算。
当我们进行二进制的加法的时候,当两个比特位相加的结果为2的时候,就需要向前进一位,但是我们可以先使用 ^ 操作来进行无进位的加法,当两个比特位相加的结果为2时,不进行进位而得到的结果,然后再使用 & 操作,来得到什么时候该进位,然后将 & 的结果向左移动一位,将上面的两个结果再循环进行上面的操作,直到 & 得到的结果为0的时候,就得到了两数之和的结果。

3.3 Java代码实现
class Solution {public int getSum(int a, int b) {while(b != 0) {int x = a ^ b;int y = a & b;a = x;b = y << 1;}return a;}
}
4. 只出现一次的数字
https://leetcode.cn/problems/single-number-ii/
4.1 题目要求
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99]
输出:99
提示:
- 1 <= nums.length <= 3 * 104
- -231 <= nums[i] <= 231 - 1
- nums 中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
class Solution {public int singleNumber(int[] nums) {}
}
4.2 做题思路
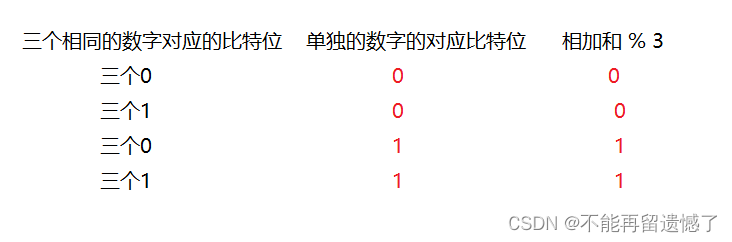
通过题目,我们可以知道,除了那个只出现了一次的数字之外,其他的数字都出现了一次,所以呢,我们可以将数组中的每个元素的32个比特位分别相加,将结果 % 3,就会得到那个只出现一次的数字的对应比特位。
4.3 Java代码实现
class Solution {public int singleNumber(int[] nums) {int ret = 0;for(int i = 0; i < 32; i++) {int tmp = 0;for(int n : nums) {tmp += (n >> i) & 1;}ret |= (tmp % 3) << i;}return ret;}
}
5. 消失的两个数字
https://leetcode.cn/problems/missing-two-lcci/
5.1 题目要求
给定一个数组,包含从 1 到 N 所有的整数,但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗?
以任意顺序返回这两个数字均可。
示例 1:
输入: [1]
输出: [2,3]
示例 2:
输入: [2,3]
输出: [1,4]
提示:
- nums.length <= 30000
class Solution {public int[] missingTwo(int[] nums) {}
}
5.2 做题思路
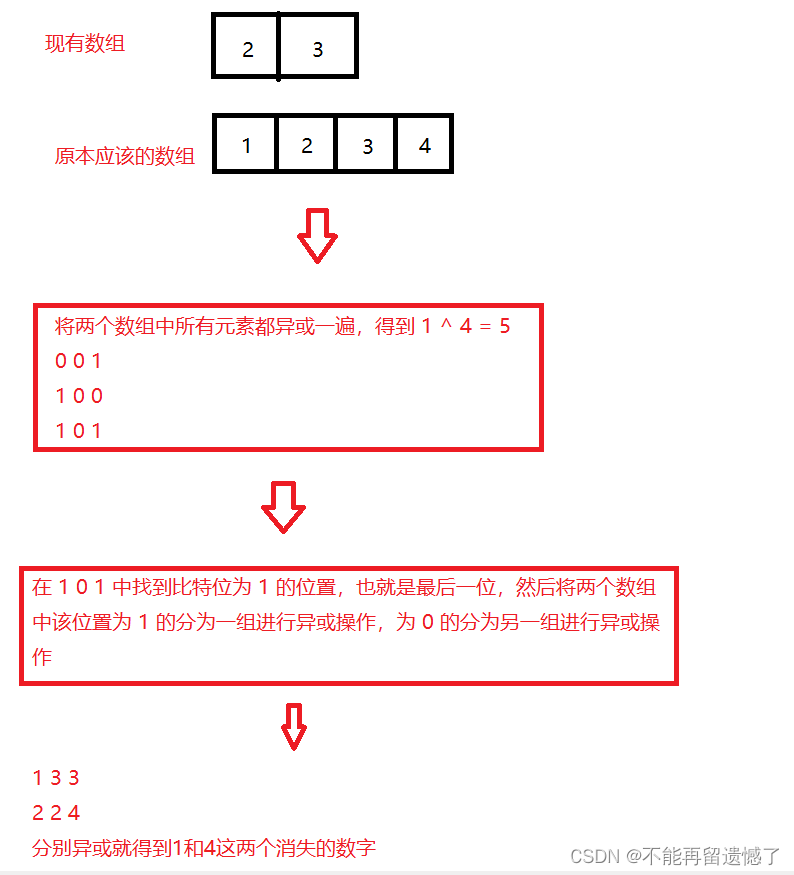
这个题目跟上面的消失的一个数字其实是类似的,只不过这里出现了两个消失的数字,我们不可能一次就找到两个消失的数字,但是我们可以分两次找。可以将这道题目转换为数组中只出现了一次的数字,这里大家可以看看我之前写过的一篇文章寻找单身狗,但是呢一个数组中只能找到一个只出现了一次的数字,如果要想找到两个只出现了一次的数字,我们可以将这两个消失的数组分别给分到两个不同的数组中,然后在每一个数组中找那个只出现了一次的数字,最终这两个消失的数字都会被找到。那么,如何将这两个消失的数字分在两个不同的数组中呢?同样是将原本的数组和现有的数组中的所有元素都进行异或操作,相同的元素异或为0,最后剩下的其实就是这两个消失的数字异或的结果,然后我们需要在这个异或的结果中找到比特位为 1 的位置,因为异或,相异为 1 ,相同为0,当找到这个为 1 的比特位之后,就可以将这些元素进行分组了,该比特位为 1 的为一组,为 0 的为另一组。
5.3 Java代码实现
class Solution {public int[] missingTwo(int[] nums) {int[] ret = new int[2];int tmp = 0;for(int n : nums) tmp ^= n;for(int i = 1; i <= nums.length + 2; i++) tmp ^= i;int flg = 0; //用来记录异或结果比特位为1的位置for(int i = 0; i < 32; i++) {if(((tmp >> i) & 1) == 1) {flg = i;break;}}for(int n : nums) {if(((n >> flg) & 1) == 1) ret[0] ^= n;else ret[1] ^= n;}for(int i = 1; i <= nums.length + 2; i++) {if(((i >> flg) & 1) == 1) ret[0] ^= i;else ret[1] ^= i;}return ret;}
}
总结
通过本篇博客,我们深入了解了位运算算法及其在计算机领域中的重要性和应用。位运算算法是一项强大的工具,它基于二进制位的操作,能够高效地处理二进制数据,提升程序的性能和效率。
在实际应用中,我们可以利用位运算算法来实现各种位级别的操作,如位掩码、位操作、整数运算优化、位图算法和压缩算法等。这些算法和技巧可以在底层系统编程、嵌入式系统、网络协议和算法优化等领域发挥重要作用。
然而,在使用位运算算法时,也需要注意一些优化技巧和注意事项。我们需要注意位运算的优先级、位移操作的性能和溢出问题,以及如何利用位运算进行快速乘法、除法和判断奇偶性等操作。深入理解这些技巧,能够更好地应用位运算算法,提高代码的效率和准确性。
位运算算法是计算机科学中一个广泛应用的领域,通过深入学习和实践,我们可以进一步探索和发现更多有趣的位运算技巧和应用。在日常编程中,合理运用位运算算法,能够帮助我们解决一些复杂的问题,实现更高效和可靠的程序。
希望本篇博客能够为读者提供一个全面而清晰的位运算算法入门指南,让大家对位运算算法有更深入的了解,并能够应用于实际开发中。通过不断学习和探索,我们可以进一步提升自己的编程能力,并在算法领域中取得更多的成就。
感谢您的阅读,希望本篇博客对您有所帮助。如果您有任何问题或反馈,欢迎留言交流。祝愿您在位运算算法的学习和应用中取得成功!
相关文章:

【算法系列篇】位运算
文章目录 前言什么是位运算算法1.判断字符是否唯一1.1 题目要求1.2 做题思路1.3 Java代码实现 2. 丢失的数字2.1 题目要求2.2 做题思路2.3 Java代码实现 3. 两数之和3.1 题目要求3.2 做题思路3.3 Java代码实现 4. 只出现一次的数字4.1 题目要求4.2 做题思路4.3 Java代码实现 5.…...

机器学习的测试和验证(Machine Learning 研习之五)
关于 Machine Learning 研习之三、四,可到秋码记录上浏览。 测试和验证 了解模型对新案例的推广效果的唯一方法是在新案例上进行实际尝试。 一种方法是将模型投入生产并监控其性能。 这很有效,但如果你的模型非常糟糕,你的用户会抱怨——这…...

RNN循环神经网络
目录 一、卷积核与循环核 二、循环核 1.循环核引入 2.循环核:循环核按时间步展开。 3.循环计算层:向输出方向生长。 4.TF描述循环计算层 三、TF描述循环计算 四、RNN使用案例 1.数据集准备 2.Sequential中RNN 3.存储模型,acc和lose…...
安防视频监控/视频集中存储/云存储平台EasyCVR无法播放HLS协议该如何解决?
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。音视频流媒体视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、…...

Docker技术--Docker的安装
1..Docker的安装方式介绍 Docker官方提供了三种方式可以实现Docker环境的安装。分别为:Script、yum、rpm。在实际的环境中建议使用yum或者是rpm。 2..Docker的yum安装 # 1.下载docker wget https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo -O /etc/yum.re…...
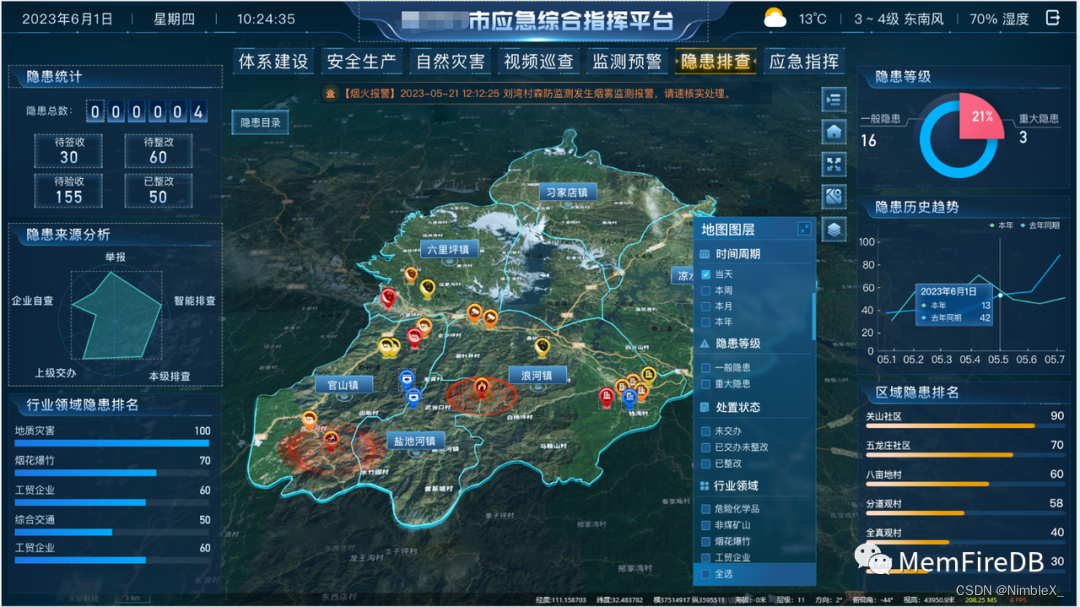
客户案例|MemFire Cloud助推应急管理业务,打造百万级数据可视化大屏
「导语」 硬石科技,成立于2018年,总部位于武汉,是一家专注于应急管理行业和物联感知预警算法模型的技术核心的物联网产品和解决方案提供商。硬石科技作为一家高新技术企业,持有6项发明专利,拥有100余项各类平台认证和资…...
蒲公英路由器如何设置远程打印?
现如今,打印机已经是企业日常办公中必不可少的设备,无论何时何地,总有需要用到打印的地方,包括资料文件、统计报表等等。 但若人在外地或分公司,有文件急需通过总部的打印机进行打印时,由于不在同一物理网络…...
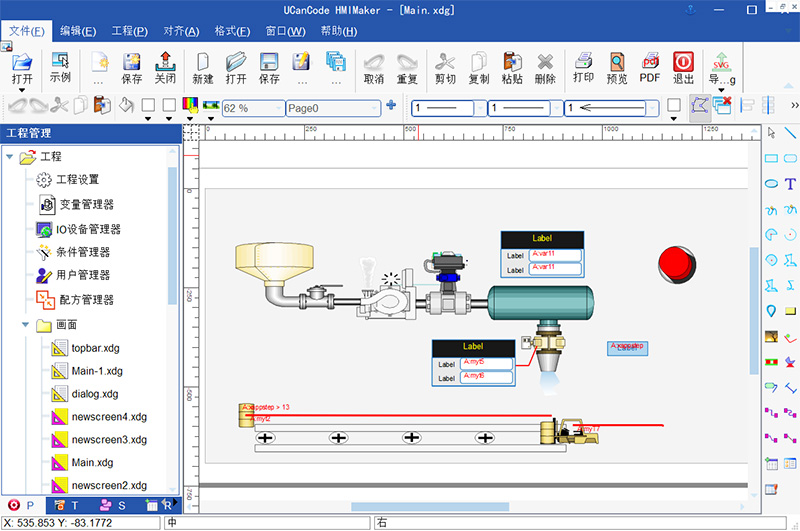
国产自主可控C++工业软件可视化图形架构源码
关于国产自主代替的问题是当前热点,尤其是工业软件领域。 “一个功能强大的全自主C跨平台图形可视化架构对开发自主可控工业基础软件至关重要!” 作为全球领先的C工业基础图形可视化软件提供商,UCanCode软件有自己的思考,我们认…...

【linux命令讲解大全】022.网络管理工具和命令概述
文章目录 lsattr命令语法选项参数实例 nmcli补充说明语法选项OPTIONSOBJECT 实例 systemctl补充说明任务 旧指令 新指令 实例 开启防火墙22端口 从零学 python lsattr命令 用于查看文件的第二扩展文件系统属性。 语法 lsattr(选项)(参数) 选项 -E:可显示设备属…...

应急响应流程及思路
应急响应流程及思路 一:前言 对于还没有在项目中真正接触、参与过应急响应的同学来说,“应急响应”这四个字见的最多的就是建筑工地上的横幅 —— 人人懂应急,人人会响应。这里的应急响应和我们网络安全中的应急响应有着某种本质的相似&…...

网页自适应
自适应 那就要最好提前商量好 是全局自适应 或者是 局部自适应 一般网站页面纵向滚动条都是无法避免的 都是做横向适配也就是宽度 那就不能写死宽度像素 局部自适应 一般对父元素设置百分比就行 里面的子元素就设置固定像素、 比如一些登录 全局自适应 也就是要对每个元素…...

什么是Sui Kiosk,它可以做什么,如何赋能创作者?
创作者和IP持有者需要一些工具帮助他们在区块链上实现其商业模式。Sui Kiosk作为Sui上的一种原语可以满足这种需求,为创作者提供动态选项,使他们能够在任何交易场景中设置完成交易的条件。 本文将向您介绍为什么要在SuiFrens中使用Sui Kiosk,…...

【MySQL】mysql connect
目录 一、准备工作 1、创建mysql用户 2、删除用户 3、修改用户密码 3.1、自己改自己密码 3.2、root用户修改指定用户的密码 4、数据库的权限 4.1、给用户授权 4.2、回收权限 二、连接mysql client 1、安装mysql客户端库 2、验证是否引入成功 三、 mysql接口 1、初…...
基于 vue2 发布 npm包
背景:组件化开发需要,走了一遍发布npm包的过程,采用很简单的模式实现包的发布流程,记录如下。 项目参考:基于vue的时间播放器组件,并发布到npm_timeplay.js_xmy_wh的博客-CSDN博客 1、项目初始化 首先&a…...

基于Axios完成前后端分离项目数据交互
一、安装Axios npm i axios -S 封装一个请求工具:request.js import axios from axios// 创建可一个新的axios对象 const request axios.create({baseURL: http://localhost:9090, // 后端的接口地址 ip:porttimeout: 30000 })// request 拦截器 // 可以自请求…...

时序预测 | MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比
时序预测 | MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比 目录 时序预测 | MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比效果一览基本描述程序设计参考资料 效果一览 基本描述 MATLAB实现基于PSO-BiLSTM、BiLSTM时间序列预测对比。 1.Matlab实现PSO-BiLSTM和BiLSTM…...
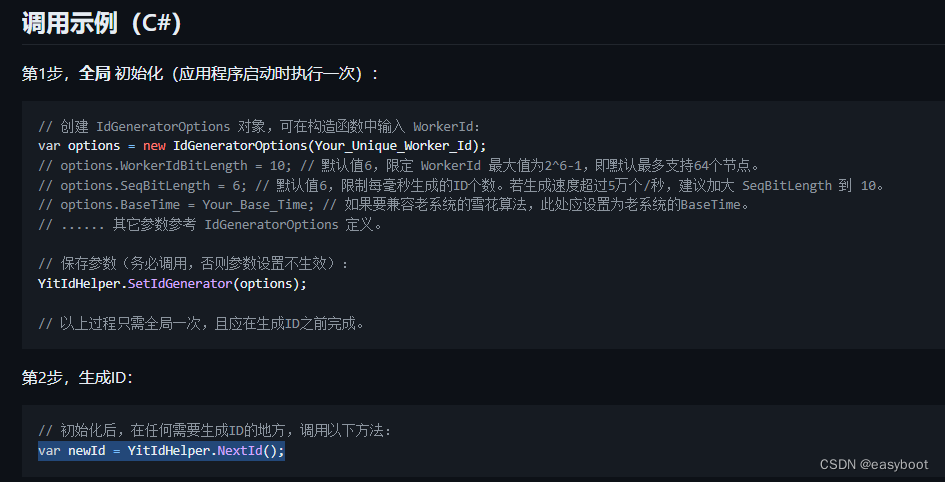
C# 生成唯一ID
1.首先通过nuget安装yitter.idgenerator 下面的三行代码搞定...

python怎么提取视频中的音频
目录 操作步骤 1. 安装MoviePy库: 2. 导入MoviePy库和所需的模块: 3. 提取音频: 可能遇到的问题 1. 编解码器支持: 2. 依赖项安装: 3. 文件路径问题: 4. 内存消耗: 5. 输出文件大小&a…...

学习设计模式之建造者模式,但是宝可梦
前言 作者在准备秋招中,学习设计模式,做点小笔记,用宝可梦为场景举例,有错误欢迎指出。 建造者模式 建造者模式是一种创建型模式,主要针对于某一个类有特别繁杂的属性,并且这些属性中有部分不是必须的。…...

数学建模:变异系数法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 变异系数法 变异系数法的设计原理是: 若某项指标的数值差异较大,能明确区分开各被评价对象,说明该指标的分辨信息丰富,因而应给该指标以较大的权重…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
