【LeetCode】双指针妙解有效三角形的个数

Problem: 611. 有效三角形的个数
文章目录
- 题目分析
- 讲解算法原理
- 复杂度
- Code
题目分析
首先我们来分析一下本题的思路
- 看到题目中给出的示例

- 题目的意思很简单,就是将给到的数字去做一个组合,然后看看这三条边是否可以构成三角形。那判断的方法不用我说,相信大家如果读过小学的话应该都明白的,即
三角形两边之和大于第三边则可以构成三角形

其实对于三角形的判断我们无需去判别三次,而是可以进行取巧👇
- 看到这里,我们可以去找出三个数中较大的那个数,然后只需去比较
a + b > c即可,而对于a + c > b与b + c > a则不用去进行一个比较,因为此时[c]已经是最大的了,那再去加上a或者b的话一定会更大,所以无需去做比较 - 不过呢,这需要我们先找出最大的那个数,即要去做一个排序的操作进行优化

- 上面的这种思路对我们本题的解法很有帮助,望读者先行理解
讲解算法原理
然后我们根据上面的思路来分析一下本题的算法原理
- 暴力枚举
- 首先的话第一种,大家都能想到的就是【暴力枚举】,下面的话我写了一手伪代码,也就是通过三层的for循环,去一一进行枚举的操作。不过呢这很明显,时间复杂度为 O ( n 3 ) O(n^3) O(n3) 一定会造成超时。
for(int i = 0;i < n; ++i)
{for(int j = i + 1;j < n; ++j){for(int k = j + 1;k < n; ++k){check(nums[i], nums[j], nums[k]);}}
}
我们可以来看一下运行后的结果

再来试着分析一下复杂度:
- 对于
check()函数而言,如果我们还是使用上面判断三次的方式来看三条边是否可以构成三角形,那么最终因为外层的循环就会使得时间复杂度到达 3 O ( n 3 ) 3O(n^3) 3O(n3); - 但是呢,如果我们使用的是取巧的办法,那需要先去使用【sort】做一个排序。只判断一次的话最终的时间复杂度为 O ( N l o g N + N 3 ) O(NlogN + N^3) O(NlogN+N3)
- 那么后者一定是要比前者的复杂度来得低的,所以我们要考虑到换一种解法
- 利用单调性,结合双指针进行求解
接下去我就来介绍一下【双指针】这种解法
- 首先的话,上面说到过了,我们需要将整个数据先去做一个优化,使其呈现升序的样子,接下去呢我们要先拿到这个最大的数作为
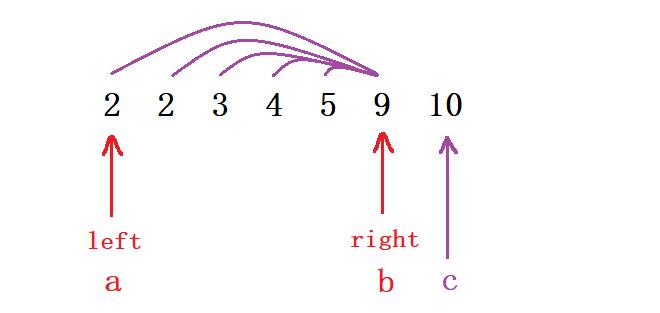
[c];然后呢我们拿左指针left从左向右进行遍历,拿右指针right从右往左开始遍历 - 那我们现在看到
a + b = 11 > c,那么就可以利用我们上面所介绍的这种思想,无需再去多判断

- 因为我们在一开始做了优化,数据是呈现升序排列的。例如像下面这里
2 + 9、3 + 9、4 + 9等等这些都是要比10要来得大的,那其实我们根本无需再去判断这些数据,从【2】~【5】这5组数据均可以组成三角形,那此时如果我们要得到这个5的话只需要让right - left即可 - 那既然前面的数据都是与9进行结合,那这个9的话我们就使用完了,接下去让
right--进行下一个数据的判断即可
- 接下去我们再来看第二种,此时我们可以看到
2 + 5 = 7 < 10,那么此时我们可以继续去观察从【2】~【5】的这一堆数,它们一定是比5来得小的,那我们也无需再去多做比较了,对于这个【2】来说我们就可以舍弃了
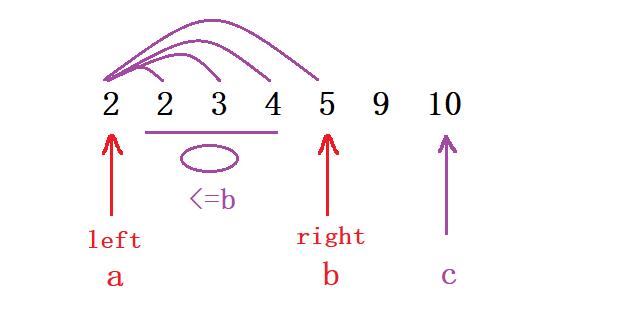
所以我们在来总结一下上面这种解法
- 先固定最大的数
- 在最大数的左区间内,使用双指针算法,快速统计出符合要求的三元组个数

复杂度
- 时间复杂度:
来说一下双指针这种解法的时间复杂度, 首先的话我们要在N个数内找到那个最大的数,然后的话还要使用【双指针】去遍历从
0 ~ n - 1这N - 1个数,那么时间复杂度即为 O ( N 2 ) O(N^2) O(N2)
- 空间复杂度:
对于空间复杂度来说,没有去开辟任何的空间,所以为 O ( 1 ) O(1) O(1)
Code
来展示一下最终的代码
class Solution {
public:int triangleNumber(vector<int>& nums) {// 1.优化sort(nums.begin(), nums.end());// 2.利用双指针解决问题int ret = 0, n = nums.size();for(int i = n - 1; i >= 2; --i) // 先固定最大的数{// a : nums[left]// b : nums[right]// c : nums[i]int left = 0, right = i - 1;while(left < right){if(nums[left] + nums[right] > nums[i]){ret += right - left;right--;}else{left++;}}}return ret;}
};

相关文章:

【LeetCode】双指针妙解有效三角形的个数
Problem: 611. 有效三角形的个数 文章目录 题目分析讲解算法原理复杂度Code 题目分析 首先我们来分析一下本题的思路 看到题目中给出的示例 题目的意思很简单,就是将给到的数字去做一个组合,然后看看这三条边是否可以构成三角形。那判断的方法不用我说&a…...
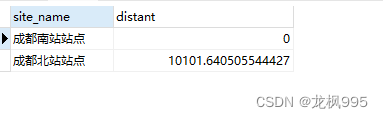
mysql 计算两点之间距离
先说一下我们可能会用到的一些场景,这样同学们可以先评估,该篇文章是否对你有帮助! 场景: 假设 美团,我点外卖时,系统会让我先进行定位,比如我定位在了 A 点,系统就会给我推荐&…...

c语言自定义头文件是什么情况下使用?一般在什么情况下引用自定义的头文件?一般在自定义头文件中写什么代码?
c语言自定义头文件是什么情况下使用?一般在什么情况下引用自定义的头文件?一般在自定义头文件中写什么代码? C语言自定义头文件是一种用来封装函数和变量声明的文件,它通常用于将一组相关的函数和变量的声明集中在一个地方&#…...

electron应用打包成功纪念一下
electron应用打包成功纪念一下,以前曾经行过后来打包各种报错,现在有空就尝试解决一下 首先安装nvm能够方便切换node版本 curl -o- https://raw.githubusercontent.com/nvm-sh/nvm/v0.34.0/install.sh | bash 顺利安装后你用nvm list查看node列表时会…...

远程办公中安全远程访问解决方案
什么是安全远程访问 安全的远程访问是一个至关重要的过程,可让您使用互联网从远处完全控制某人的设备。为了确保安全,为受保护的远程访问采取了额外的身份验证和加密措施。 为什么安全远程访问解决方案很重要 当 IT 技术人员从远处帮助人们解决计算机…...

StartUp启动框架-Android启动性能
简述 当谈论Android应用程序的启动性能时,StartUp启动框架是一个不可忽视的关键工具。它旨在优化应用程序的启动过程,确保用户在打开应用时能够迅速获得流畅、高效的体验。让我们来深入了解StartUp框架的作用和重要性,以及它是如何改善Andro…...

Positive Technologies:五分之四的网络攻击具有针对性
Positive Technologies 对 2023 年第二季度的相关网络威胁进行了分析。报告显示,自今年年初以来,有针对性的攻击数量增加了 10%,目前占 78%。专家们注意到利用漏洞的大规模攻击和大量用户个人数据的泄露。此外,在此期间࿰…...

clickhouse的另类表引擎
clickhouse常用的MergeTree引擎外,还有特殊的引擎 1,memory引擎,顾名思义,数据是存储在内存中,数据不会被压缩也不会倍格式化转换数据在内存中保存的形态与查询时看到的如出一辙,重启ck数据丢失 2ÿ…...

Uniapp新版本打包后覆盖安装,新增的页面无法跳转,需退出重新启动才可以打开的解决方案
最近写uniapp项目,发现一个坑,在新版本覆盖安装后直接打开APP,新增的页面竟然无法跳转,需要重新启动才可以正常打开,在网上查了很多方法,最终总结下来有以下几点: 1.看打的是debug包还是releas…...
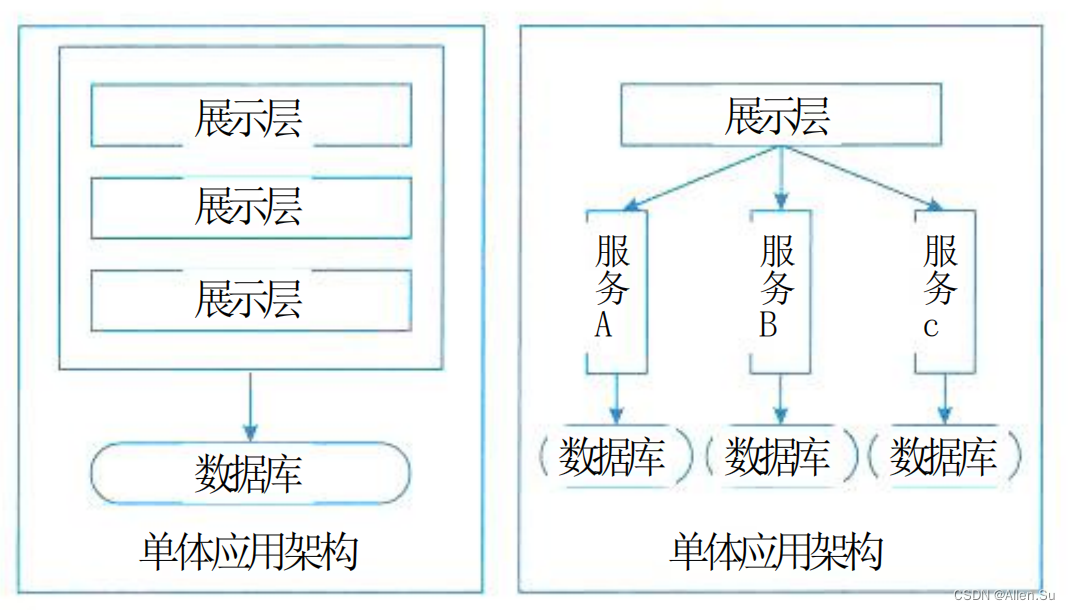
系统架构设计高级技能 · 面向服务架构设计理论与实践
点击进入系列文章目录 系统架构设计高级技能 面向服务架构设计理论与实践 一、SOA的相关概念1.1SOA的定义1.2 业务流程与业务流程执行语言 二、SOA的发展史三、SOA与微服务的区别三、SOA的参考架构四、SOA的主要协议规范五、SOA的设计标准要求六、SOA的作用与设计原则七、SOA的…...
)
QT注册界面练习(信号与槽实现页面跳转)
一、注册界面练习思路以及具体代码 在完成注册页面搭建的前提下,通过信号与槽机制实现多组件之间的相互通信,实现页面跳转。 基本步骤: 首先,将注册页面的登录按钮与成功登陆信号绑定,当用户名与密码均匹配时…...

MySQL从入门到精通【进阶篇】之 主从复制详解
文章目录 0.前言1. 主从复制简介2. 主从复制的工作流程主从复制过程中的日志文件作用(Binary Log)和中继日志(Relay Log) 3. MySQL主从复制的配置4. 参考资料 0.前言 MySQL的主从复制和读写分离是数据库领域的基本概念࿰…...
vue使用qrcodejs2生成二维码
目录 概要 构建展示的vue组件qrcode.vue 组件的使用 概要 项目中用到需要展示二维码的样式,想到了qrcode 例如: 前提:安装包 npm install qrcodejs2 --save 构建展示的vue组件qrcode.vue <template><div style"width: …...

python注释
任何编程语言都少不了注释,Python也不例外,以下是Python注释的具体用法: 单行注释 Python编程语言的单行注释常以#开头,单行注释可以作为单独的一行放在被注释代码行之上,也可以放在语句或者表达式之后。 实例&…...

update-alternatives详解
1.功能作用 update-alternatives是dpkg的实用工具,用来维护系统命令的符号链接,以决定系统默认使用什么命令。 在Debian系统中,我们可能会同时安装有很多功能类似的程序和可选配置,如Web浏览器程序(firefox,konquero…...

JavaScript 编写更好的条件语句
在任何编程语言中,代码需要根据不同的条件在给定的输入中做不同的决定和执行相应的动作。 例如,在一个游戏中,如果玩家生命点为0,游戏结束。在天气应用中,如果在早上被查看,显示一个日出图片,如…...

聊聊PBE算法
序 本文主要研究一下PBE算法 PBE PBE即Password Based Encryption,基于口令的加密,它是一种组合算法,即一般是哈希对称算法,比如PBEWithMD5AndDES,就是用MD5做哈希,用DES做加解密,而其密钥则…...
用MFC打开外部程序
在MFC(Microsoft Foundation Classes)中,你可以使用ShellExecute函数来打开Notepad并加载指定的文件。ShellExecute函数是Windows API的一部分,它可以执行与操作系统相关的操作,例如打开文件、运行程序等。 以下是在M…...

基于全新电脑环境安装pytorch的GPU版本
前言: 距离第一次安装深度学习的GPU环境已经过去了4年多(当时TensorFlow特别麻烦),现在发现安装pytorch的GPU版本还是很简单方便的,流程记录如下。 安装步骤: 步骤一:官网下载Anaconda Free…...

[当前就业]2023年8月25日-计算机视觉就业现状分析
计算机视觉就业现状分析 前言:超越YOLO:计算机视觉市场蓬勃发展 如今,YOLO(You Only Look Once)新版本的发布周期很快,每次迭代的性能都优于其前身。每 3 到 4 个月就会推出一个升级版 YOLO 变体…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
