深度剖析:数据服务API的安全性与隐私保护
随着互联网技术的飞速发展,数据服务API已经成为了企业和个人获取、处理和分析数据的重要工具。然而,数据服务API的安全问题也日益凸显,尤其是在用户隐私保护方面。本文将深入剖析数据服务API的安全性与隐私保护问题,并结合产品FDL(FineDataLink)进行案例分析。
一、数据服务API的安全性挑战
1.数据泄露:由于数据服务API通常涉及到用户的敏感信息,如身份证号、手机号、邮箱地址等,因此数据泄露的风险极高。一旦数据泄露,用户的隐私将面临极大的威胁。
2.身份伪造:攻击者可能通过伪造身份信息,利用数据服务API进行非法操作,如盗取用户资金、篡改用户数据等。
3.系统攻击:数据服务API的服务器可能受到黑客的攻击,导致用户数据被窃取或篡改。
4.法规遵从性:数据服务API需要遵循各种法规要求,如欧盟的《通用数据保护条例》(GDPR)等。这就要求数据服务API提供商在设计和实现过程中,充分考虑到法规遵从性问题。
二、数据服务API的隐私保护措施
1.加密技术:采用加密技术对用户数据进行加密传输和存储,确保数据在传输和存储过程中的安全性。
2.访问控制:实施严格的访问控制策略,确保只有授权用户才能访问相应的数据。同时,对不同用户分配不同的权限,实现精细化的数据管理。
3.审计与监控:建立完善的审计和监控机制,对数据服务API的使用情况进行实时监控,及时发现并处理异常行为。
4.数据脱敏:对涉及用户隐私的数据进行脱敏处理,如使用哈希算法、伪名化等技术,确保用户隐私不被泄露。
5.法律法规遵循:遵循相关法规要求,如GDPR等,确保数据服务API在设计、开发和使用过程中,充分保障用户隐私权益。
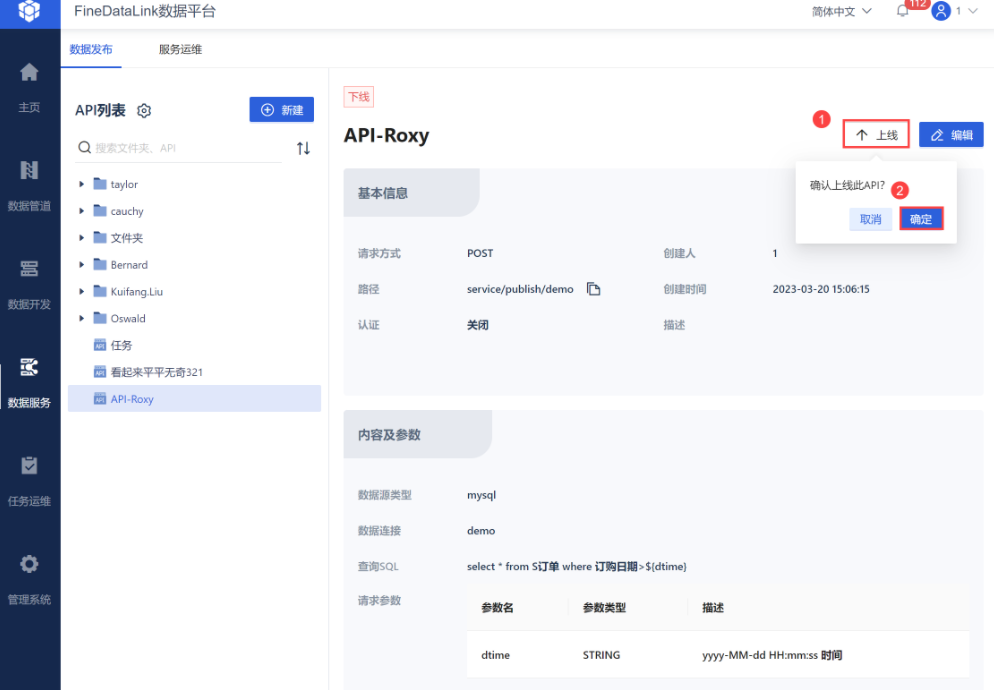
三、案例分析:FDL(FineDataLink)的数据服务API安全与隐私保护实践
FDL是一家专注于提供数据服务API的企业,其在安全性与隐私保护方面有着丰富的实践经验。以下是FDL在数据服务API安全与隐私保护方面的几个亮点:
1.采用HTTPS协议:FDL的数据服务API采用HTTPS协议进行数据传输,确保数据在传输过程中的安全性。
2.多重身份验证:FDL的数据服务API支持多重身份验证,如短信验证码、指纹识别等,确保只有合法用户才能访问相应的数据。
3.访问控制策略:FDL的数据服务API采用基于角色的访问控制策略,根据用户的角色分配不同的权限,实现精细化的数据管理。
4.审计与监控:FDL的数据服务API具备完善的审计和监控功能,可以对用户的访问行为进行实时监控,及时发现并处理异常行为。
5.数据脱敏处理:FDL的数据服务API在处理涉及用户隐私的数据时,采用哈希算法、伪名化等技术进行脱敏处理,确保用户隐私不被泄露。
结论:随着大数据时代的到来,数据服务API已经成为了企业和个人获取、处理和分析数据的重要工具。然而,数据服务API的安全性与隐私保护问题也日益凸显。因此,企业和开发者需要在设计和实现过程中,充分考虑到安全性与隐私保护问题,以确保用户的信息安全和隐私权益得到充分保障。作为一家专注于提供数据服务API的企业,FDL在安全性与隐私保护方面有着丰富的实践经验,值得借鉴和学习。
了解更多数据仓库与数据集成关干货内容请关注>>>
数据集成技术分享集锦
免费试用、获取更多信息,点击了解更多>>>
FineDataLink-帆软FDL|一站式数据集成平台|数据同步|数据清洗|API接口数据发布|告别T+1
相关文章:

深度剖析:数据服务API的安全性与隐私保护
随着互联网技术的飞速发展,数据服务API已经成为了企业和个人获取、处理和分析数据的重要工具。然而,数据服务API的安全问题也日益凸显,尤其是在用户隐私保护方面。本文将深入剖析数据服务API的安全性与隐私保护问题,并结合产品FDL…...
MediaPlayer音频与视频的播放介绍
作者:向阳逐梦 Android多媒体中的——MediaPlayer,我们可以通过这个API来播放音频和视频该类是Androd多媒体框架中的一个重要组件,通过该类,我们可以以最小的步骤来获取,解码和播放音视频。 它支持三种不同的媒体来源…...
【Terraform学习】Terraform模块基础操作(Terraform模块)
本站以分享各种运维经验和运维所需要的技能为主 《python》:python零基础入门学习 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8》暂未更新 《docker学习》暂未更新 《ceph学习》ceph日常问题解…...
)
改进的KMeans 点云聚类算法 根据体元中的点数量计算点密度,并获取前K个点密度最大的体元作为初始聚类中心(附 matlab 代码)
KMeans函数的主要逻辑如下: 使用InitCenter函数初始化聚类中心,该函数根据体元密度选择初始聚类中心。该函数的输入参数包括数据(data)、聚类中心数量(centerNum)和体元数量(voxelNum)。根据点云的取值范围计算包围盒的体积(V)和体元边长(d)。根据体元边长将点云数…...

php user.ini详解
0x00 前言 本篇主要是讲解分析一下user.ini相关的内容。因为这个知识点涉及到文件上传的绕过 0x01 正文 .user.ini 文件是PHP的配置文件,用于自定义PHP的配置选项。该文件通常位于PHP安装目录的根目录下,或者在特定的网站目录下。 .user.ini 文件是一…...

用 PHP 和 JavaScript 显示地球卫星照片
向日葵 8 号气象卫星是日本宇宙航空研究开发机构设计制造的向日葵系列卫星之一,重约 3500 公斤,设计寿命 15 年以上。该卫星于 2014 年 10 月 7 日由 H2A 火箭搭载发射成功,主要用于监测暴雨云团、台风动向以及持续喷发活动的火山等防灾领域。…...

Ubantu安装mongodb,开启远程访问和认证
最近因为项目原因需要在阿里云服务器上部署MongoDB,操作系统为Ubuntu,网上查阅了一些资料,特此记录一下步骤。 1.运行apt-get install mongodb命令安装MongoDB服务(如果提示找不到该package,说明apt-get的资源库版本比…...
高手速成|数据库脚本生成工具
高手速成|数据库脚本生成工具 文章目录 高手速成|数据库脚本生成工具前言1、软件的安装及使用2、建立新工程3、创建Conceptual Data Model(概念数据模型)4、将E-R图转化为其他数据库模型5、导出DBMS代码(Sql执行脚本)6、执行sql脚…...

振动国标2009GB/T 19873.2-2009/ISO 13373-2:2005笔记
国标原文 1.时域,要求,采样率大于最高频率10倍(最低频率?) 2.频域,要求采样率大于最高频率2倍。 3.3.2 积分和微分,二次积分。 3.3.3 均方根。 3.4 滤波 4.1 奈奎斯特图、极坐标图、坎贝尔…...
SpringBoot中自定义starter
SpringBoot自动装配原理: EnableAutoConfiguration注解开启自动装配功能,该注解通常放在应用的主类上。spring.factories文件位于META-INF目录下的配置文件中定义各个自动装配类的全限定名 当SpringBoot启动时,会加载classpath下所有的spri…...

git-tf clone 路径有空格处理方案
git-tf clone 路径存在空格情况下,运行命令报错; 需要对路径进行双引号处理...

IP 地址与域名是一对多的关系。一个 IP 地址可以对应多个域名,但一个域名只对应一个 IP地址。这句话如何理解?
假设你有一个大型公司,拥有许多服务器和网站。每台服务器都有自己的IP地址,就像每台手机有一个电话号码一样。然而,你可能不想让客户记住一堆复杂的数字来访问你的网站。这时候,你可以为每个网站分配一个易记的域名,比…...

DNS解析分类
DNS(域名系统)解析是将域名转换为对应的IP地址的过程。根据不同的功能和角色,DNS解析可以分为以下几种分类: 递归解析(Recursive Resolution):递归解析是指DNS客户端向本地DNS服务器(…...
部署你自己的导航站-dashy
现在每天要访问的网页都太多了,尽管chrome非常好用,有强大的标签系统。但是总觉的少了点什么。 今天我就来分享一个开源的导航网站系统 dashy。这是一个国外的大佬的开源项目 github地址如下:https://github.com/Lissy93/dashy 来简单说一下…...

运用谱分解定理反求实对称矩阵
文章目录 谱分解定理定理的运用 谱分解定理 设三阶实对称矩阵 A A A,若矩阵 A A A 的特征值为 λ 1 , λ 2 , λ 3 \lambda_1,\lambda_2,\lambda_3 λ1,λ2,λ3,对应的单位化特征向量分别为 α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α…...

Qt——Qt工作原理:事件驱动、信号与槽机制
Qt工作原理:事件驱动、信号与槽机制 Qt作为一个现代的GUI(图形用户界面)框架,采用了事件驱动的编程范式,并引入了信号与槽机制,以实现高度交互和松耦合的程序设计。下面详细解释了相关概念,以及…...

find ./* -type d -empty -exec touch {}/.gitkeep \;
这是一个 Linux 下的 find 命令,用于在所有空目录中创建 .gitkeep 文件。让我们来分解一下这个命令做了什么:- find ./* : 在当前目录及其子目录中查找。 -type d : 只查找目录类型的文件。 -empty : 只找出那些空的目…...

计算机行业前景展望
计算机行业的前景展望是非常广阔的。随着技术的快速发展和应用领域的不断拓展,计算机行业将继续扮演着重要的角色。以下是一些计算机行业前景的关键方面: 人工智能(AI)和机器学习(ML):AI和ML技术…...
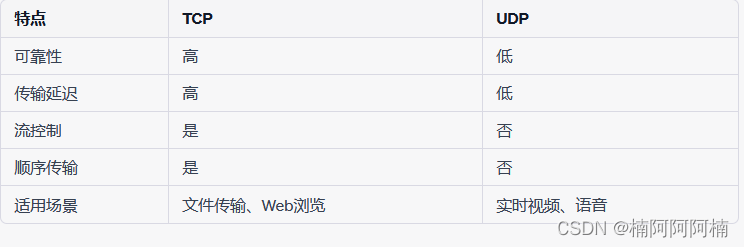
TCP/UDP原理
文章目录 一、端口1. 端口的定义和作用2.服务端和客户端的区别3.常见的知名端口号有 二、TCP的原理1.TCP头部封装格式2.TCP可靠性机制三次握手确认机制四次挥手RST结束连接窗口机制 3.完整性校验4.TCP特征5.TCP的适用场景 三、UDP的原理1.UDP头部封装格式2.UDP特征3.UDP的适用场…...
操作符算数转换题
目录 1.交换两个变量(不创建临时变量) 2.统计二进制中1的个数 3.打印整数二进制的奇数位和偶数位 4.求两个数二进制中不同位的个数 5.【一维数组】有序序列合并 6.获得月份天数 7.变种水仙花数 8.选择题总结tips 这篇博文主要分享操作符&算…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
