【考研数学】概率论与数理统计 —— 第二章 | 一维随机变量及其分布(1,基本概念与随机变量常见类型)
文章目录
- 引言
- 一、一维随机变量及其分布
- 1.1 随机变量
- 1.2 分布函数
- 二、随机变量常见类型及分布
- 2.1 离散型随机变量
- 2.2 连续型随机变量及概率密度函数
- 写在最后
引言
暑假接近尾声了,争取赶一点概率论部分的进度。
一、一维随机变量及其分布
1.1 随机变量
设随机试验 E E E 的样本空间为 Ω \Omega Ω , X X X 为定义于样本空间 Ω \Omega Ω 上的函数,对于任意 w ∈ Ω w \in \Omega w∈Ω ,总存在唯一确定的 X ( w ) X(w) X(w) 与之对应,称 X ( w ) X(w) X(w) 为随机变量,一般记为 X X X 。
随机变量一定的取值范围本质上就是随机事件,若随机变量某个范围内取不到任何值,本质上为不可能事件,若某个范围包含了随机变量所有可能的取值,本质上就是必然事件。
1.2 分布函数
设 X X X 为随机变量,对任意的实数 x x x ,称函数 F ( x ) = P F(x)=P F(x)=P { X ≤ x X \leq x X≤x } 为随机变量 X X X 的分布函数。
其有如下四个性质:
(1) 0 ≤ F ( x ) ≤ 1 ; 0 \leq F(x) \leq 1; 0≤F(x)≤1;
(2) F ( x ) F(x) F(x) 是 x x x 的单调不减函数;
(3) F ( x ) F(x) F(x) 关于 x x x 右连续;
(4) F ( − ∞ ) = 0 , F ( + ∞ ) = 1. F(-\infty)=0,F(+\infty)=1. F(−∞)=0,F(+∞)=1.
若有一个函数满足以上四个条件,可称其为某个随机变量的分布函数。如 F ( 3 x − 1 ) F(3x-1) F(3x−1) 仍为分布函数,但 F ( 1 − 3 x ) F(1-3x) F(1−3x) 不是分布函数,当 x → + ∞ x \to +\infty x→+∞ , F ( 1 − 3 x ) F(1-3x) F(1−3x) 极限为 0 不为 1 ; F ( x 2 ) F(x^2) F(x2) 也不是分布函数,因为当 x → + ∞ x \to +\infty x→+∞ , F ( x 2 ) F(x^2) F(x2) 极限为 1 不为 0 。
设随机变量 X X X 的分布函数为 F ( x ) F(x) F(x) ,则
(1) P P P { X < a X < a X<a } = F ( a − 0 ) ; =F(a - 0); =F(a−0);
(2) P P P { a < X ≤ b a < X\leq b a<X≤b } = F ( b ) − F ( a ) ; =F(b)-F(a); =F(b)−F(a);
(3) P P P { a ≤ X < b a \leq X < b a≤X<b } = F ( b − 0 ) − F ( a − 0 ) ; =F(b - 0)-F(a-0); =F(b−0)−F(a−0);
(4) P P P { a ≤ X ≤ b a \leq X \leq b a≤X≤b } = F ( b ) − F ( a − 0 ) ; =F(b)-F(a-0); =F(b)−F(a−0);
(5) P P P { a < X < b a < X < b a<X<b } = F ( b − 0 ) − F ( a ) ; =F(b - 0)-F(a); =F(b−0)−F(a);
(6) P P P { X = a X =a X=a } = F ( a ) − F ( a − 0 ) ; =F(a)-F(a-0); =F(a)−F(a−0);
二、随机变量常见类型及分布
2.1 离散型随机变量
设 X X X 为随机变量,若 X X X 的可能取值是有限个或可列个,称 X X X 为离散型随机变量。
设离散型随机变量 X X X 的可能取值为 x i ( i = 1 , 2 , … ) x_i(i=1,2,\dots) xi(i=1,2,…) ,其对应的概率为 P P P { X = x i X=x_i X=xi } = p i =p_i =pi ,称 P P P { X = x i X=x_i X=xi } = p i =p_i =pi 或下表

为随机变量 X X X 的分布律。
离散型随机变量 X X X 的分布律满足:
(1) p i ≥ 0 ( i = 1 , 2 , … ) . p_i \geq 0(i=1,2,\dots). pi≥0(i=1,2,…).
(2) ∑ i = 1 + ∞ p i = 1. \sum_{i=1}^{+\infty}p_i=1. ∑i=1+∞pi=1.
(3)分布函数 F ( x ) = P F(x)=P F(x)=P { X ≤ x X \leq x X≤x } 为阶梯函数,且 F ( x ) F(x) F(x) 的间断点即为随机变量 X X X 的可能取值。
什么是阶梯函数呢,就是图像是像台阶那样的。举个例子,记随机变量 X X X 为投掷一枚均匀的骰子朝上的点数,则 X X X 可取 1 , 2 , 3 , 4 , 5 , 6 1,2,3,4,5,6 1,2,3,4,5,6 ,且 P P P { X = i X=i X=i } = 1 6 ( i = 1 , 2 , … , 6 ) =\frac{1}{6}(i=1,2,\dots,6) =61(i=1,2,…,6) ,其分布律如下表所示:

分布函数图像为:

注意,阶梯是先右再上的阶梯,因为是离散的取值,所以在两个取值之间的分布函数值应为前一个取值所对应函数值。
2.2 连续型随机变量及概率密度函数
设随机变量 X X X 的分布函数为 F ( x ) F(x) F(x) ,若存在非负、可积的函数 f ( x ) f(x) f(x) ,使得对任意实数 x x x ,有 F ( x ) = ∫ − ∞ x f ( t ) d t , F(x)=\int_{-\infty}^xf(t)dt, F(x)=∫−∞xf(t)dt, 称 X X X 为连续型随机变量,函数 f ( x ) f(x) f(x) 为随机变量 X X X 的概率密度函数或概率密度。
连续型随机变量概率密度有如下结论:
(1) f ( x ) ≥ 0 ; f(x) \geq 0; f(x)≥0;
(2) ∫ − ∞ + ∞ f ( t ) d t = 1 ; \int_{-\infty}^{+\infty}f(t)dt=1; ∫−∞+∞f(t)dt=1;
(3)分布函数 F ( x ) F(x) F(x) 为连续函数,但不一定可导;
(4) P P P { X = a X=a X=a } = F ( a ) − F ( a − 0 ) = 0 =F(a)-F(a-0)=0 =F(a)−F(a−0)=0 ,故连续型随机变量在任意一点处的概率为 0 。
(5)设分布函数为 F ( x ) F(x) F(x) ,则概率密度函数为 f ( x ) = { F ′ ( x ) , x 为 F ( x ) 的可导点 0 , x 为 F ( x ) 的不可导点 f(x) = \begin{cases} F'(x), & x \text{为} F(x) 的可导点 \\ 0, & x为F(x) 的不可导点\\ \end{cases} f(x)={F′(x),0,x为F(x)的可导点x为F(x)的不可导点 (6)存在既不是离散型又不是连续型的随机变量,如随机变量 X X X 的分布函数表达式为 F ( x ) = { 0 , if x < 0 x 2 , if 0 ≤ x < 1 1 if x ≥ 1 F(x) = \begin{cases} 0, & \text{if } x < 0 \\ \frac{x}{2}, & \text{if } 0 \leq x < 1 \\ 1 & \text{if } x \geq1 \end{cases} F(x)=⎩ ⎨ ⎧0,2x,1if x<0if 0≤x<1if x≥1 显然 F ( x ) F(x) F(x) 满足分布函数的四个特性,但其不是阶梯函数,所以 X X X 非离散型随机变量。又因为 F ( x ) F(x) F(x) 存在间断点,所以 X X X 也非连续型随机变量,其图像如下图所示。

写在最后
下一篇我们将介绍一些常见的随机变量分布。
相关文章:

【考研数学】概率论与数理统计 —— 第二章 | 一维随机变量及其分布(1,基本概念与随机变量常见类型)
文章目录 引言一、一维随机变量及其分布1.1 随机变量1.2 分布函数 二、随机变量常见类型及分布2.1 离散型随机变量2.2 连续型随机变量及概率密度函数 写在最后 引言 暑假接近尾声了,争取赶一点概率论部分的进度。 一、一维随机变量及其分布 1.1 随机变量 设随机试…...
CSS判断手机暗黑模式
手机有个功能到了晚上会自动变成深色也就是暗黑模式.这种情况下网页会自动变颜色.如果想自由控制暗黑模式下的html样式的话,可以用如下方式: media (prefers-color-scheme: dark) {/*html, body {*//*filter: invert(1) hue-rotate(180deg);*//*}*/.maill{margin-left: 0;marg…...
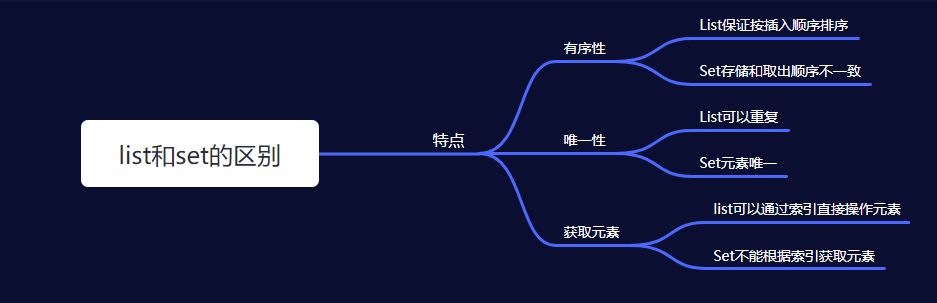
【java中的Set集合】HashSet、LinkedHashSet、TreeSet(最通俗易懂版!!)
目录 一、HashSet集合 1.HashSet集合的特点 2.HashSet常用方法 二、LinkedHashSet集合 LinkedHashSet集合的特点 三、TreeSet集合 1.TreeSet集合的特点 2.TreeSet的基本使用 四、HashSet、LinkedHashSet、TreeSet的使用场景 五、list和set集合的区别 一、HashSet集合 …...

python中的文件操作
我们平常对文件的基本操作,大概可以分为三个步骤(简称文件操作三步走): ① 打开文件 ② 读写文件 ③ 关闭文件 【注意事项】 注意:可以只打开和关闭文件,不进行任何读写 文件打开 open函数ÿ…...

spark支持深度学习批量推理
背景 在数据量较大的业务场景中,spark在数据处理、传统机器学习训练、 深度学习相关业务,能取得较明显的效率提升。 本篇围绕spark大数据背景下的推理,介绍一些优雅的使用方式。 spark适用场景 大数据量自定义方法处理、类sql处理传统机器…...

代码随想录打卡—day52—【子序列问题】— 8.31 最大子序列
共性 做完下面三题,发现三个的dp数组中i都是以 i 为结束的字串。 1 300. 最长递增子序列 300. 最长递增子序列 AC: class Solution { public:int dp[10010]; // 表示以i结束的子序列最大的长度/*if(nums[j] > nums[i])dp[j] max(dp[j],dp[i] …...

gcc4.8.5升级到gcc4.9.2
第1步:获取repo [rootlocalhost SPECS]# wget --no-check-certificate https://copr.fedoraproject.org/coprs/rhscl/devtoolset-3/repo/epel-6/rhscl-devtoolset-3-epel-6.repo -O /etc/yum.repos.d/devtoolset-3.repo --2021-12-07 20:53:26-- https://copr.fedo…...
:常用函数)
Golang 中的 archive/zip 包详解(三):常用函数
Golang 中的 archive/zip 包用于处理 ZIP 格式的压缩文件,提供了一系列用于创建、读取和解压缩 ZIP 格式文件的函数和类型,使用起来非常方便,本文讲解下常用函数。 zip.OpenReader 定义如下: func OpenReader(name string) (*R…...

微服务架构七种模式
微服务架构七种模式 目录概述需求: 设计思路实现思路分析 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better result,wait for change,challenge Survive.…...
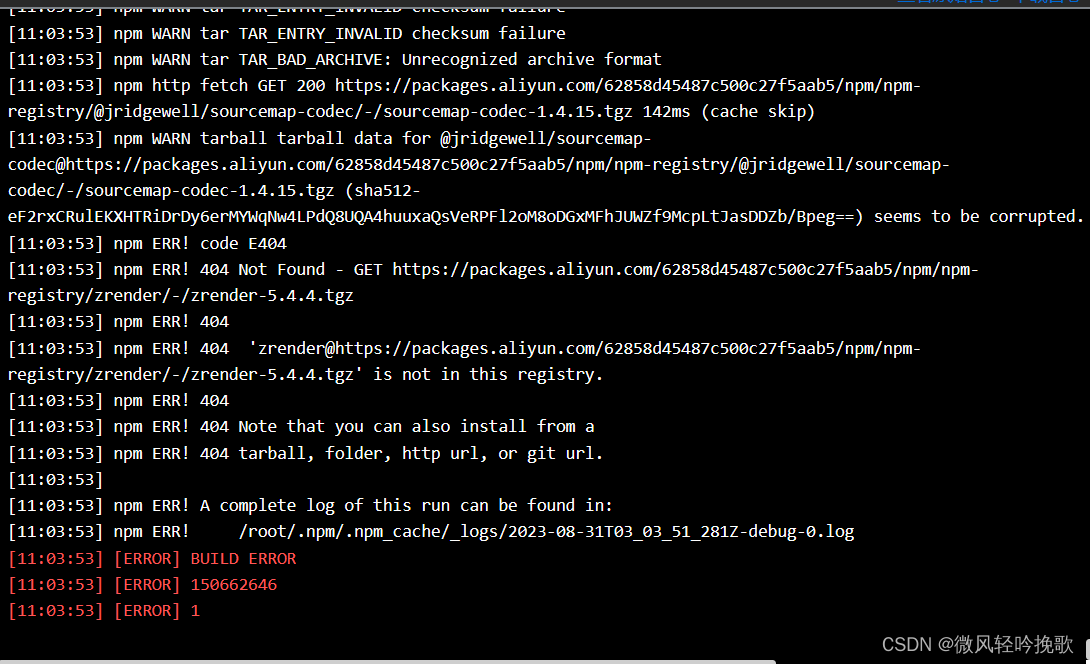
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm...
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm… 原因应该是某些jar包缓存中没有需要改变镜像将包拉下来 npm config set registry http://registry.npm.taobao.org npm install npm run build...

element-plus的周选择器 一周从周一开始
1、代码 1)、template中 <el-date-picker v-model"value1" type"week" format"[Week] ww" placeholder"巡访周" change"change"value-format"YYYY-MM-DD" /> 2)、方法中 import…...

Android 9.0 pms获取应用列表时过滤掉某些app功能实现
1.前言 在9.0的系统rom定制化开发中,对系统定制的功能也是很多的,在一次产品开发中,要求在第三方app获取应用列表的时候,需要过滤掉某些app,就是不显示在app应用列表中,这就需要在pms查询app列表时过滤掉这些app就可以了,接下来就实现这些功能 2.pms获取应用列表时过滤掉…...

HTML <thead> 标签
实例 带有 thead、tbody 以及 tfoot 元素的 HTML 表格: <table border="1"><thead><tr><th>Month</th><th>Savings</th></tr></thead><tfoot><tr><td>Sum</td><td>$180<…...

谷歌发布Gemini以5倍速击败GPT-4
在Covid疫情爆发之前,谷歌发布了MEENA模型,短时间内成为世界上最好的大型语言模型。谷歌发布的博客和论文非常可爱,因为它特别与OpenAI进行了比较。 相比于现有的最先进生成模型OpenAI GPT-2,MEENA的模型容量增加了1.7倍…...
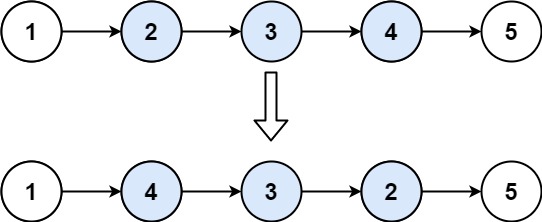
力扣92. 局部反转链表
92. 反转链表 II 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 示例 1: 输入:head [1,2,3,4,5], left 2, right 4 输出&am…...

九、适配器模式
一、什么是适配器模式 适配器模式(Adapter)的定义如下:将一个类的接口转换成客户希望的另外一个接口,使得原本由于接口不兼容而不能一起工作的那些类能一起工作。 适配器模式(Adapter)包含以下主要角色&…...
使用spring自带的发布订阅来实现发布订阅
背景 公司的项目以前代码里面有存在使用spring自带发布订阅的代码,因此稍微学习一下如何使用,并了解一下这种实现方式的优缺点。 优点 实现方便,代码方面基本只需要定义消息体和消费者,适用于小型应用程序。不依赖外部中间件&a…...
Walmart电商促销活动即将开始,如何做促销活动?需要注意什么?
近日,沃尔玛官宣Baby Days优惠活动将于9月1日正式开始!卖家可以把握机会,通过设置促销定价,以最优惠的婴儿相关产品价格吸引消费者,包括汽车座椅、婴儿车、尿布袋、家具、床上用品、消耗品、婴儿服装、孕妇装等。注意本…...
Matlab(画图进阶)
目录 大纲 1.特殊的Plots 1.1 loglog(双对数刻度图) 1.3 plotyy(创建具有两个y轴的图形) 1.4yyaxis(创建具有两个y轴的图) 1.5 bar 3D条形图(bar3) 1.6 pie(饼图) 3D饼图 1.7 polar 2.Stairs And Ste阶梯图 3.Boxplot 箱型图和Error Bar误差条形图 3.1 boxplot 3.2 …...

人生的回忆
回忆是人类宝贵的精神财富,它们像一串串珍珠,串联起我们生活中的每一个片段。 回忆是时间的见证者,它们承载着我们成长、经历、悲欢离合的点点滴滴。 回忆让我们重温过去的欢笑与眼泪,感受那些已经逝去的时光。它们就像一本翻开的…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...
