pytorch中 nn.Conv2d的简单用法
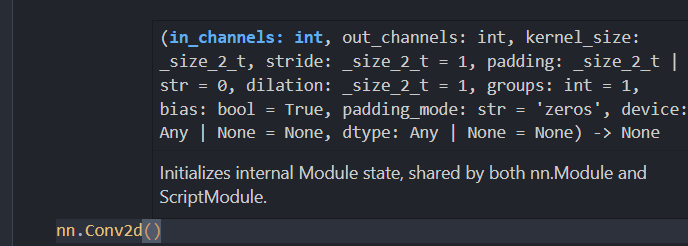
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True,padding_mode='zeros')
参数介绍:
-
in_channels:卷积层输入通道数 -
out_channels:卷积层输出通道数 -
kernel_size:卷积层的卷积核大小 -
padding:填充长度 -
stride:卷积核移动的步长 -
dilation:是否采用空洞卷积 -
groups:是否采用分组卷积 -
bias:是否添加偏置参数 -
padding_mode:padding的模式
如果输入大小为:数量N即批处理大小(batch size),输入通道数C_in,输入高度H_in,输入宽度C_in。输出大小为:数量N,输出通道数C_out,输出高度H_out,输出宽度C_out。
i n p u t : ( N , C i n , H i n , W i n ) o u t p u t : ( N , C o u t , H o u t , W o u t ) input: \quad (N, C_{in},H_{in},W_{in}) \\ output: \quad (N,C_{out}, H_{out}, W_{out}) input:(N,Cin,Hin,Win)output:(N,Cout,Hout,Wout)
之间的转换为:
( N i , C o u t ) = b i a s ( C o u t ) + ∑ k = 0 C i n − 1 w e i g h t ( C o u t , k ) ∗ ( N i , k ) (N_i,C_{out}) = bias(C_{out}) + \sum_{k=0}^{C_{in}-1}weight(C_{out},k) * (N{i},k) (Ni,Cout)=bias(Cout)+k=0∑Cin−1weight(Cout,k)∗(Ni,k)
H o u t = [ H i n + 2 ∗ p a d d i n g [ 0 ] − d i l a t i o n [ 0 ] ∗ ( k e r n a l s i z e [ 0 ] − 1 ) − 1 s t r i d e [ 0 ] + 1 ] H_{out} = [ \frac {H_{in} + 2 * padding[0] - dilation[0] *(kernal_size[0] - 1) - 1}{stride[0]} + 1] Hout=[stride[0]Hin+2∗padding[0]−dilation[0]∗(kernalsize[0]−1)−1+1]
W o u t = [ W i n + 2 ∗ p a d d i n g [ 1 ] − d i l a t i o n [ 1 ] ∗ ( k e r n e l s i z e [ 1 ] − 1 ) − 1 s t r i d e [ 1 ] + 1 ] W_{out} = [ \frac {W_{in} + 2 * padding[1] - dilation[1] * (kernel_size[1] - 1) - 1} {stride[1]} + 1] Wout=[stride[1]Win+2∗padding[1]−dilation[1]∗(kernelsize[1]−1)−1+1]
对于二维简化的:
W i n , H i n 输入的宽、高 W o u t , H o u t 输出的宽,高 F 卷积核的大小 S 步长 P 边界填充 W_{in},H_{in} \quad 输入的宽、高 \\ W_{out},H_{out} \quad 输出的宽,高 \\ F \quad 卷积核的大小 \\ S \quad 步长 \\ P \quad 边界填充 Win,Hin输入的宽、高Wout,Hout输出的宽,高F卷积核的大小S步长P边界填充
那么输出的宽、高为:
W o u t = W i n − F W + 2 P S + 1 H o u t = H i n − F H + 2 P S + 1 W_{out} = \frac {W_{in} - F_{W} + 2P} S + 1 \\ H_{out} = \frac {H_{in} - F_{H} + 2P} S + 1 Wout=SWin−FW+2P+1Hout=SHin−FH+2P+1
在pytorch中的使用
- 直接使用(不常见)
import torch
import torch.nn as nn
# https://www.bilibili.com/video/BV1644y1h7LN/?spm_id_from=333.337.search-card.all.click&vd_source=13dfbe5ed2deada83969fafa995ccff6# 输入通道数
in_channels = 1
# 输出通道数
out_channels = 1
# 批处理大小
batch_size = 1
# 卷积核大小 (3,3)
kernel_size = 3
# 输入规格
input_size = [batch_size, in_channels, 4, 4]# nn.Conv2d使用,其他默认值
conv_layer = torch.nn.Conv2d(in_channels, out_channels, kernel_size)
# 随机输入特征图
input_feature_map = torch.randn(input_size)
# 打印输入特征图形状
print(input_feature_map.shape)
# 求出输出特征图
output_feature_map = conv_layer(input_feature_map)
# 打印出卷积核的规格
print(conv_layer.weight.shape)
# weight == out_channel * in_channel * height * weight
# 打印输出特征图大小
print(output_feature_map.shape)输出:
torch.Size([1, 1, 4, 4])
torch.Size([1, 1, 3, 3])
torch.Size([1, 1, 2, 2])
- 封装为类的形式
import torch
from torch import nn# 定义一个同样操作的卷积类
class Foo(nn.Module):def __init__(self, in_channel, out_channel):super(Foo,self).__init__()self.layer = nn.Sequential(nn.Conv2d(in_channels=in_channel, out_channels=out_channel, kernel_size=3))def forward(self, x):return self.layer(x)# 实例化一个
conv2 = Foo(1,1)
# 输出特征图, input_feature_map_2 和 input_feature_map是相同的值
output_feature_map_2 = conv2(input_feature_map_2)
print(output_feature_map_2)
输出:
tensor([[[[ 0.5144, 0.0672],[ 0.2169, -0.0591]]]], grad_fn=<ConvolutionBackward0>)
可以观察到,这两个操作相同但是结果值却不相同。这是因为虽然两者实现了相同的卷积操作,但由于它们的初始化和权重值的不同,因此输出结果可能不完全一致。 另外,对于卷积操作的结果,输出的张量形状可能会有所不同,但数值内容应该是相似的。如果希望确保两种方式得到的输出结果完全一致,可以尝试使用相同的初始化参数,并确保权重值相同。
相关文章:

pytorch中 nn.Conv2d的简单用法
torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride1, padding0, dilation1, groups1, biasTrue,padding_modezeros)参数介绍: in_channels:卷积层输入通道数 out_channels:卷积层输出通道数 kernel_size:卷积层的…...
前端项目工程化之代码规范
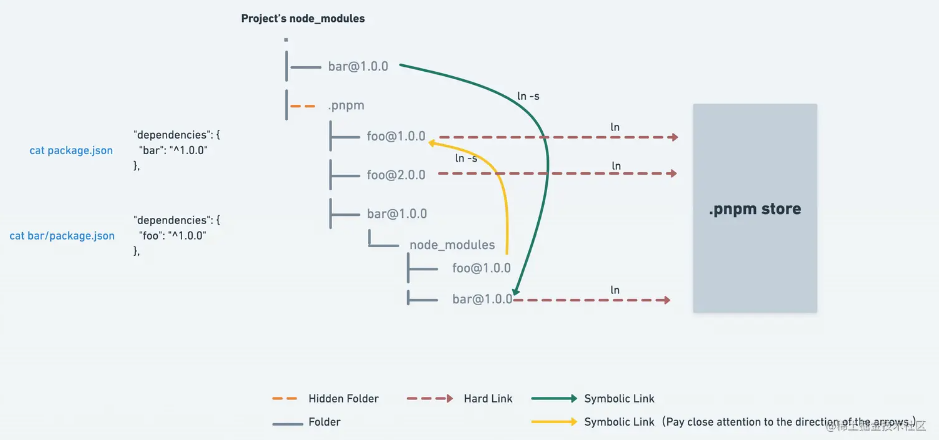
目录 一、前言二、ESLint三、Prettier四、项目实战4.1 环境依赖版本4.2 使用pnpm4.3 git提交规范 五、资源 收集六、源码地址 一、前言 前端项目工程化之代码规范是指在前端项目中定义一套代码规范,以确保项目中的代码风格和格式一致,提高代码的可读性和…...

MyBaits Generator
参考文档 MyBatis Generator Core – Introduction to MyBatis Generator MyBatis Generator 详解_enablesubpackages_isea533的博客-CSDN博客 一文解析 MyBatis Generator 的使用及配置 - 掘金 1. Introduction MyBatis Generator (MBG) 是 MyBatis MyBatis的代码生成器。…...
JavaWeb 速通Ajax
目录 一、Ajax快速入门 1.基本介绍 : 2.使用原理 : 二、Ajax经典入门案例 1.需求 : 2.前端页面实现 : 3. 处理HTTP请求的servlet实现 4.引入jar包及druid配置文件、工具类 : 5.Domain层实现 : 6.DAO层实现 : 7.Service层实现 : 8.运行测试 : 三、JQuery操作Ajax 1 …...
vscode c++编译时报错
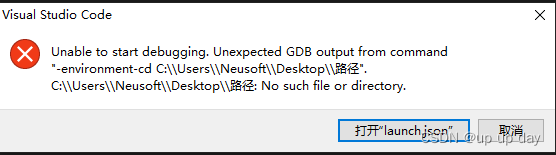
文章目录 1. 报错内容:GDB Failed with message;2. 报错内容:Unable to start debugging. 1. 报错内容:GDB Failed with message; 例如上图报错,一般就是编译器选择错误,有两种方法解决: 打开 tasks.json …...
)
基于体系结构架构设计-架构真题(十五)
基于体系结构开发设计(Architecture-Base Software Design)ABSD,是指构成体系结构的()组合驱动,ABSC方法是一个自项向下、递归细化的方法,软件系统的体系结构通过该方法细化,直到能产…...
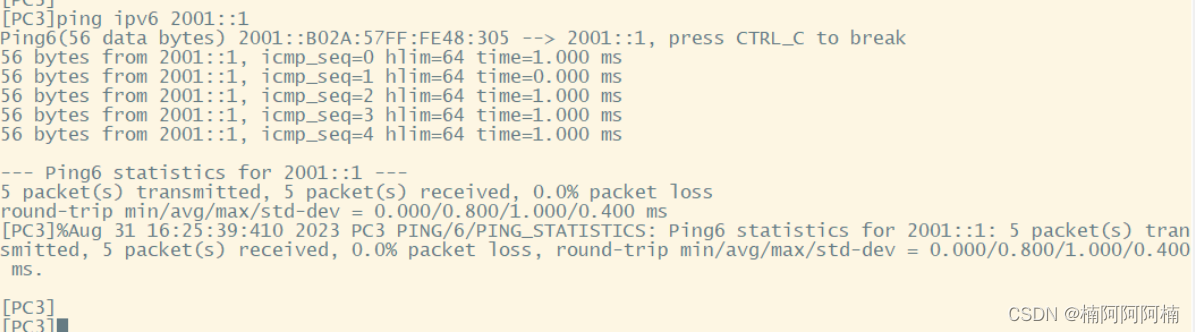
IPv6网络实验:地址自动生成与全球单播通信探索
文章目录 一、实验背景与目的二、实验拓扑三、实验需求四、实验解法1. 在R1和PC3上开启IPv6链路本地地址自动生成,测试是否能够使用链路本地地址互通2. 为R1配置全球单播地址2001::1/64,使PC3能够自动生成与R1同一网段的IPv6地址3. 测试R1和PC3是否能够使…...

深入探索前端之道:JavaScript深拷贝与浅拷贝的解析与实现
引言 前端开发中,数据的复制是一个常见的操作。尤其是在处理对象和数组时,我们需要考虑的是一个浅拷贝还是深拷贝。那么,什么是深拷贝和浅拷贝?它们在前端开发中有什么作用?如何实现这两种拷贝?这是我们在…...
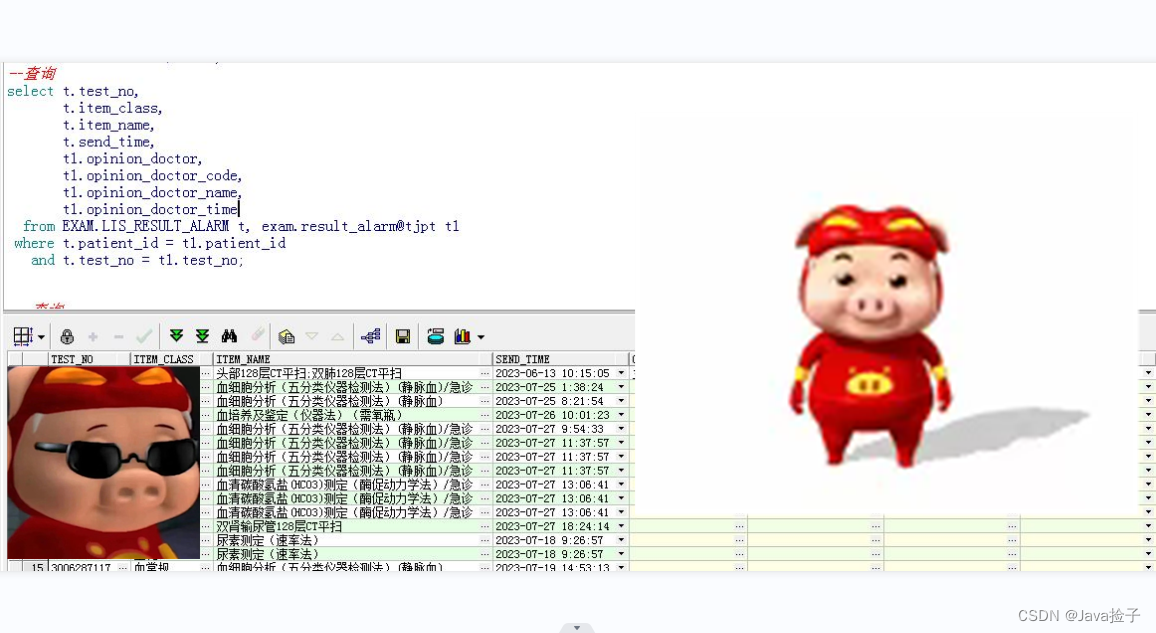
关于两个不同数据库的两张表建立数据库链接,关联查询数据
一、数据库链接 数据库链接(database link)是用于跨不同数据库之间进行连接和数据传输的工具或方法。它允许在一个数据库中访问另一个数据库中的对象和数据。 二、具体操作 以Oracle数据库为例 --1.建立链接tjpt CREATE DATABASE LINK tjpt CONNECT…...
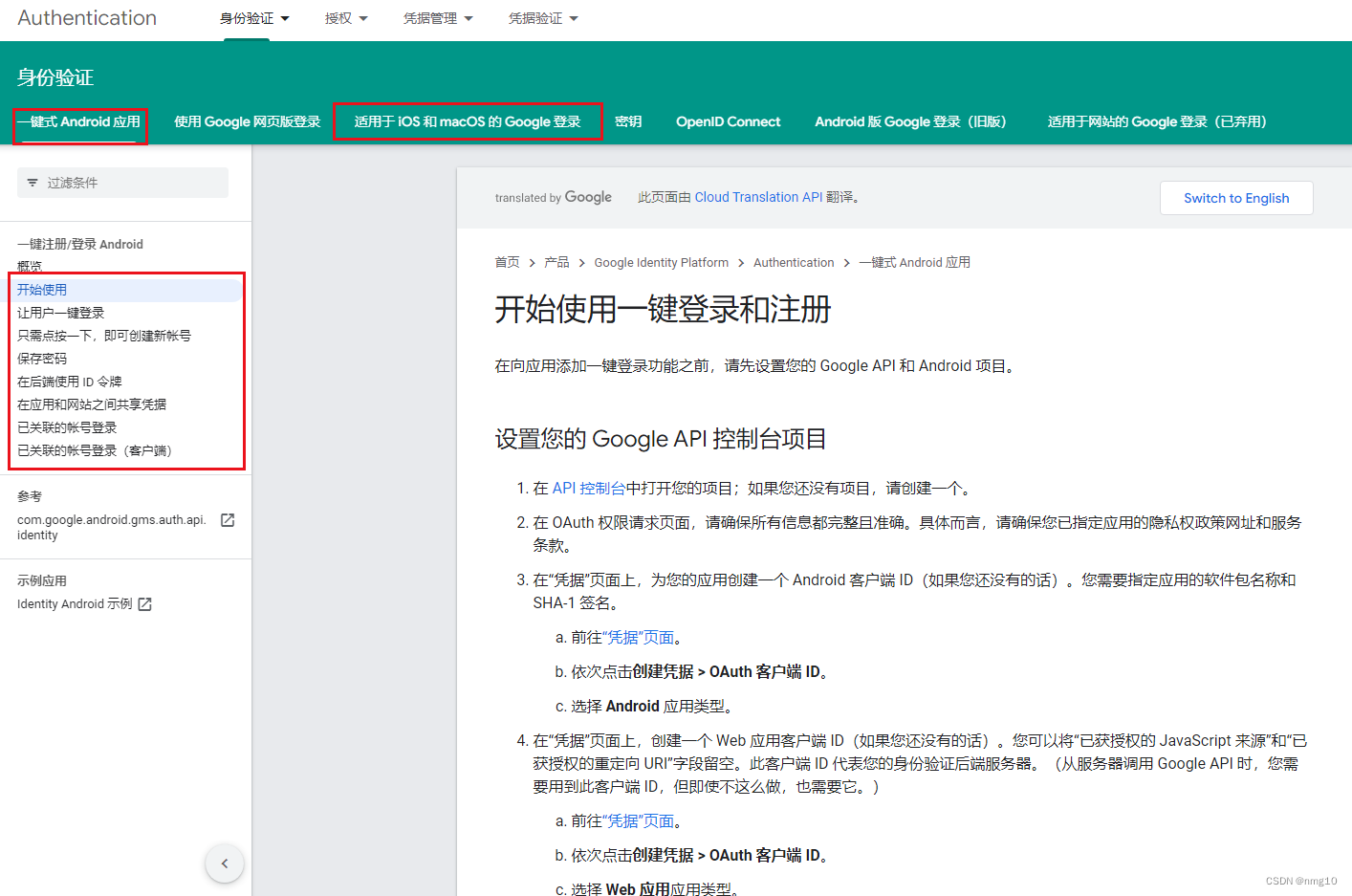
Google登录SDK
一、接入的准备工作 官方文档链接地址:开始使用一键登录和注册 按照步骤进行接入即可 二、项目参考(Unity项目) 注意:代码版本如果不适用新的Google API 请自行参考最新版本接口 SDKGoogleSignInActivity 主要用于登录的代码。Un…...

ASP.NET Core 8 的运行环境 Environment
开发流程一般有3个阶段: 开发 Development测试 Stage正式 Production 运行时环境变量可以用于根据不同的开发阶段运行不同的逻辑,比如在开发阶段的某些功能或保密信息不暴露在正式上线的代码中。 在Visual Stduio创建的模板代码中是否为开发环境Envir…...
机械臂手眼标定ZED相机——眼在手外python、matlab
目录 1.眼在手外原理 2.附上眼在手外求得手眼矩阵的python代码 3.眼在手外标定步骤 1)打印棋盘格 2)得到hand数据 3)得到camera数据 4.运行python得到手眼矩阵 1.眼在手外原理 眼在手外所求的手眼矩阵是基坐标到相机的转换矩阵 2.附上…...
前端实现动态路由(前端控制全部路由,后端返回用户角色)
优缺点 优点: 不用后端帮助,路由表维护在前端逻辑相对比较简单,比较容易上手权限少的系统用前端鉴权更加方便 缺点: 线上版本每次修改权限页面,都需要重新打包项目大型项目不适用如果需要在页面中增加角色并且控制可以访问的页…...
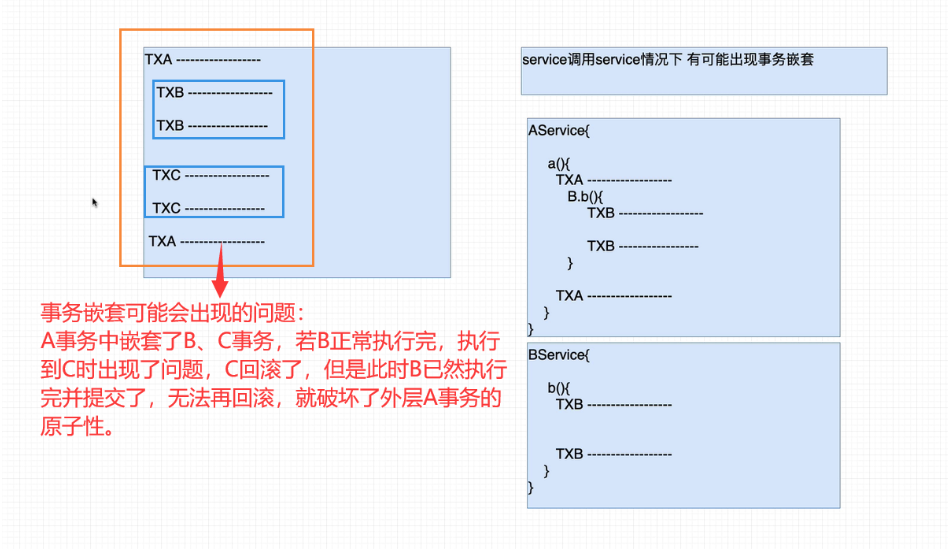
Spring5学习笔记—Spring事务处理
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: Spring专栏 ✨特色专栏: M…...
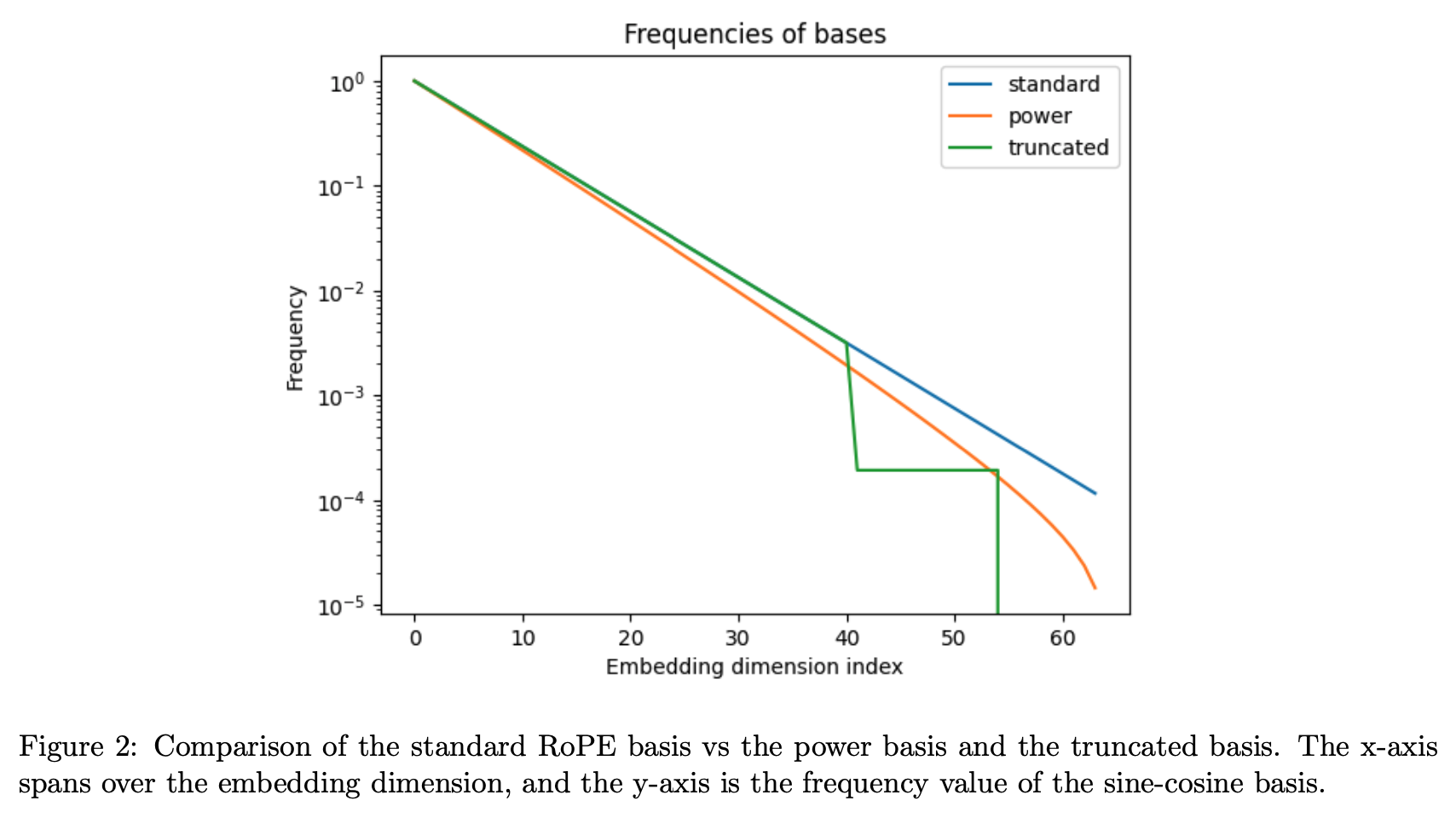
如何增长LLM推理token,从直觉到数学
背景: 最近大模型输入上文长度增长技术点的研究很火。为何要增长token长度,为何大家如此热衷于增长输入token的长度呢?其实你如果是大模型比价频繁的使用者,这个问题应该不难回答。增长了输入token的长度,那需要多次出入才能得到…...

《穷爸爸与富爸爸》时间是最宝贵的资产,只有它对所有人都是公平的
《穷爸爸与富爸爸》时间是最宝贵的资产,只有它对所有人都是公平的 罗伯特清崎,日裔美国人,投资家、教育家、企业家。 萧明 译 文章目录 《穷爸爸与富爸爸》时间是最宝贵的资产,只有它对所有人都是公平的[toc]摘录各阶层现金流图支…...
Git结合Gitee的企业开发模拟
本系列有两篇文章: 一是另外一篇《快速使用Git完整开发》,主要说明了关于Git工具的基础使用,包含三板斧(git add、git commit、git push)、Git基本配置、版本回退、分支管理、公钥与私钥、远端仓库和远端分支、忽略文…...
WEBGL(2):绘制单个点
代码如下: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevi…...
C# task多线程创建,暂停,继续,结束使用
1、多线程任务创建 private void button1_Click(object sender, EventArgs e) //创建线程{CancellationToken cancellationToken tokensource.Token;Task.Run(() > //模拟耗时任务{for (int i 0; i < 100; i){if (cancellationToken.IsCancellationRequested){return;…...
界面控件DevExpress WinForms(v23.2)下半年发展路线图
本文主要概述了官方在下半年(v23.2)中一些与DevExpress WinForms相关的开发计划,重点关注的领域将是可访问性支持和支持.NET 8。 DevExpress WinForms有180组件和UI库,能为Windows Forms平台创建具有影响力的业务解决方案。同时能…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
