Windows下将nginx等可执行文件添加为服务
Windows下将nginx等可执行文件添加为服务
- 为什么将可执行文件添加为服务?
- 将可执行文件添加为服务的步骤
- 步骤 1:下载和安装 Nginx
- 步骤 2:添加为服务
- 方法一:使用 Windows 自带的 sc 命令
- 方法二:使用 NSSM(Non-Sucking Service Manager)
- 方法三 :使用 WinSW
- 步骤 3:启动和管理服务
- 其他:删除服务

为什么将可执行文件添加为服务?
将可执行文件添加为服务有以下几个优势:
- 自动启动: 可以在系统启动时自动启动这些服务,无需手动干预。
- 稳定性: 以服务方式运行的应用程序通常会更稳定,因为它们在独立的进程中运行,不受用户登录状态的影响。
- 后台运行: 服务以后台方式运行,不会占用用户界面的空间,适合服务器环境。
- 远程管理: 可以通过服务管理工具轻松管理和监控这些服务。
将可执行文件添加为服务的步骤
这里我们使用Nginx作为一个例子,其他的可执行文件都是同理。
步骤 1:下载和安装 Nginx
前往 Nginx 官方网站下载 Windows 版本的 Nginx 可执行文件。
解压下载的文件到一个目录,例如 C:\nginx\。
步骤 2:添加为服务
方法一:使用 Windows 自带的 sc 命令
-
打开命令提示符(以管理员权限运行)。
-
使用以下命令将 Nginx 添加为服务:
sc create Nginx binPath= "C:\nginx\nginx.exe -g \"daemon off;\"" DisplayName= "Nginx" start= auto
在此示例中,Nginx 是服务的名称,C:\nginx\nginx.exe -g “daemon off;” 是 Nginx 可执行文件的完整路径和启动参数,Nginx 是服务的显示名称,start= auto 表示在系统启动时自动启动服务。
- 以下是 sc 命令的详细参数配置说明:
sc create [ServiceName] binPath= "[ExecutablePath] [Options]" DisplayName= "[DisplayName]" start= [StartType]ServiceName: 指定服务的名称,这是您在后续管理服务时需要使用的标识符。binPath: 指定可执行文件的完整路径,包括执行文件本身和可能的命令行参数。Options: 如果您的可执行文件需要附加命令行参数以正确运行,可以在这里指定。DisplayName: 指定服务的显示名称,这是在服务管理器中显示的名称。StartType: 指定服务的启动类型,有以下选项:- auto: 在系统启动时自动启动服务。
- demand: 仅在手动请求时启动服务(默认值)。
- disabled: 禁用服务,不会自动启动。
方法二:使用 NSSM(Non-Sucking Service Manager)
-
下载 NSSM: 前往 NSSM 官方网站(https://nssm.cc/)下载最新版本的 NSSM 工具。
-
安装 NSSM: 将下载的 NSSM 压缩包解压到一个文件夹中。
-
添加服务:
- 打开命令提示符(以管理员权限运行)。
- 导航到 NSSM 所在的目录。
- 运行以下命令来添加可执行文件为服务,例如将 Nginx 添加为服务:
nssm install Nginx - 在弹出的窗口中配置服务信息:
- Path: 可执行文件的完整路径(例如:C:\nginx\nginx.exe)。
- Startup directory: 可执行文件所在的目录。
- Arguments: 需要传递给可执行文件的参数,例如 -g “daemon off;”。
- Service name: 服务的名称(例如:Nginx)。
- 点击 “Install Service” 按钮。
-
启动和管理服务:
- 打开服务管理器(services.msc)。
- 在列表中找到刚刚添加的服务,右键单击进行操作。
方法三 :使用 WinSW
-
下载 WinSW: 前往 WinSW 的 GitHub 仓库(https://github.com/winsw/winsw)下载最新版本的 WinSW。
-
配置 WinSW XML 文件:
- 解压下载的 WinSW 压缩包,找到 winsw.xml 文件。
- 用文本编辑器打开 winsw.xml 文件。
- 修改 元素为服务的 ID, 元素为服务的名称, 元素为服务的描述。
- 在 元素中指定可执行文件的路径。
- 如果需要,可以配置更多选项,例如 、 等。
-
安装服务:
- 打开命令提示符(以管理员权限运行)。
- 导航到 WinSW 所在目录。
- 运行以下命令以安装服务:
winsw install
-
启动和管理服务:
-
使用以下命令启动、停止或重启服务:
winsw start winsw stop winsw restart -
或者在服务管理器中找到刚刚添加的服务,右键单击进行操作。
-
步骤 3:启动和管理服务
- 打开服务管理器(按下 Win + R 键,输入 services.msc,然后按 Enter)。
- 在服务列表中,找到刚刚创建的 Nginx 服务。
- 右键单击服务,选择启动、停止、重启等操作。
其他:删除服务
- 删除 NSSM 添加的服务:
导航到 NSSM 所在的目录;运行以下命令以删除服务,其中 “ServiceName” 是您要删除的服务名称:
nssm remove ServiceName
- 删除 WinSW 添加的服务:
导航到 WinSW 所在的目录;运行以下命令以删除服务:
winsw uninstall
- 删除使用 sc 命令添加的服务:
运行以下命令以删除服务,其中 “ServiceName” 是您要删除的服务名称:
sc delete ServiceName
相关文章:

Windows下将nginx等可执行文件添加为服务
Windows下将nginx等可执行文件添加为服务 为什么将可执行文件添加为服务?将可执行文件添加为服务的步骤步骤 1:下载和安装 Nginx步骤 2:添加为服务方法一:使用 Windows 自带的 sc 命令方法二:使用 NSSM(Non…...

视觉SLAM14讲笔记-第4讲-李群与李代数
李代数的引出: 在优化问题中去解一个旋转矩阵,可能会有一些阻碍,因为它对加法导数不是很友好(旋转矩阵加上一个微小偏移量可能就不是一个旋转矩阵),因为旋转矩阵本身还有一些约束条件,那样再求…...
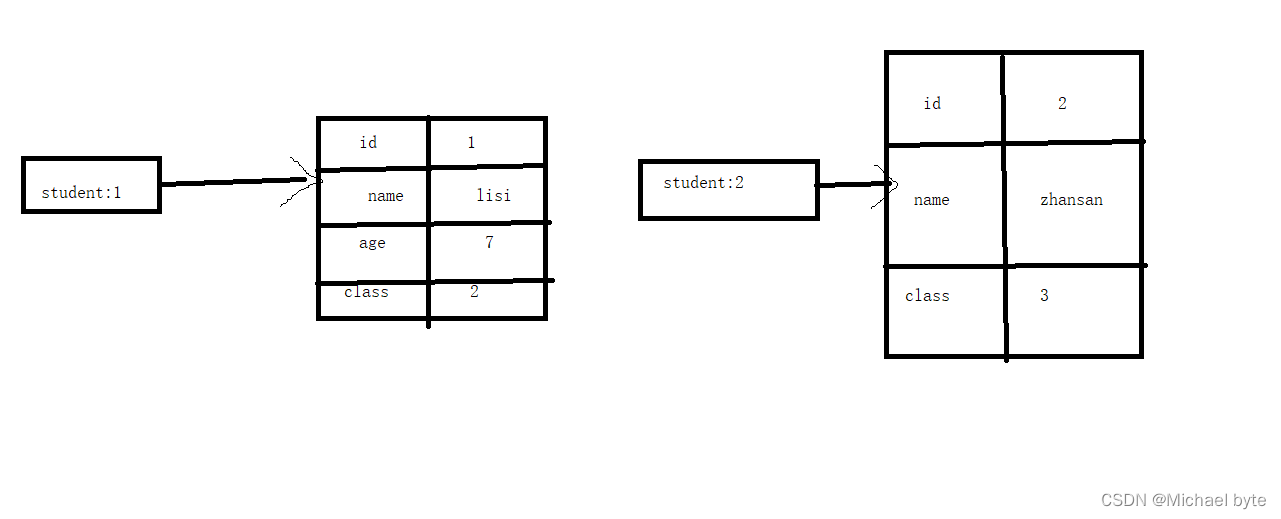
浅析Redis(1)
一.Redis的含义 Redis可以用来作数据库,缓存,流引擎,消息队列。redis只有在分布式系统中才能充分的发挥作用,如果是单机程序,直接通过变量来存储数据是更优的选择。那我们知道进程之间是有隔离性的,那么re…...

【每日一题】2337. 移动片段得到字符串
【每日一题】2337. 移动片段得到字符串 2337. 移动片段得到字符串题目描述解题思路 2337. 移动片段得到字符串 题目描述 给你两个字符串 start 和 target ,长度均为 n 。每个字符串 仅 由字符 ‘L’、‘R’ 和 ‘_’ 组成,其中: 字符 ‘L’…...
MySQL 数据库常用命令大全(详细)
文章目录 1. MySQL命令2. MySQL基础命令3. MySQL命令简介4. MySQL常用命令4.1 MySQL准备篇4.1.1 启动和停止MySQL服务4.1.2 修改MySQL账户密码4.1.3 MySQL的登陆和退出4.1.4 查看MySQL版本 4.2 DDL篇(数据定义)4.2.1 查询数据库4.2.2 创建数据库4.2.3 使…...

中国移动加大布局长三角,打造算力产业新高地
8月27日,以“数实融合算启未来”为主题的2023长三角算力发展大会在苏州举办,大会启动了长三角算力调度枢纽,携手各界推动算力产业高质量发展。 会上,移动云作为第一批算力资源提供方,与苏州市公共算力服务平台签订算力…...

话费、加油卡、视频会员等充值接口如何对接?
现在很多商家企业等发现与用户保持粘性是越来越难了,大多数的用户活跃度都很差,到底该怎么做才能改善这种情况呢? 那么我们需要做的就是投其所好,在与用户保持粘性的app或者积分商城中投入大家感兴趣的物品或者虚拟产品ÿ…...

服务器重启MongoDB无法启动
文章目录 服务器重启MongoDB无法启动背景规划实施 总结 服务器重启MongoDB无法启动 背景 数据库服务器的CPU接近告警值了,需要添加CPU资源,于是乎就在恰当的时间对服务器进行关机,待添加完资源后开机,这样就完成了CPU资源的添加…...

深度刨析数据在内存中的存储
✨博客主页:小钱编程成长记 🎈博客专栏:进阶C语言 深度刨析数据在内存中的存储 1.数据类型介绍1.1 类型的基本归类 2.整形在内存中的存储2.1 原码、反码、补码2.2 大小端介绍 3.浮点型在内存中的存储3.1 一个例子3.2 浮点数的存储规则3.3指数…...
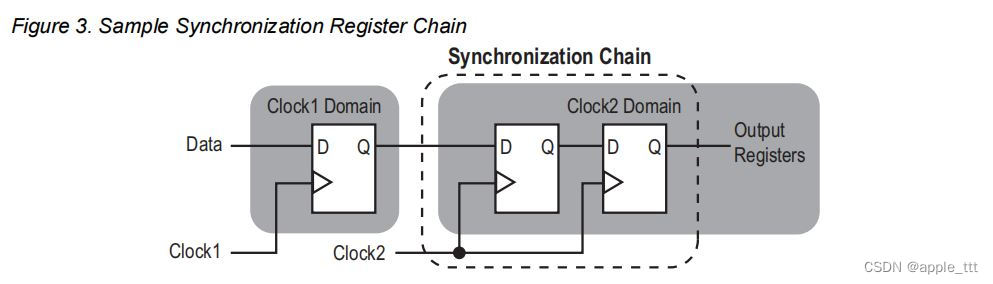
理解FPGA中的亚稳态
一、前言 大家应该经常能听说到亚稳态这个词,亚稳态主要是指触发器的输出在一段时间内不能达到一个确定的状态,过了这段时间触发器的输出随机选择输出0/1,这是我们在设计时需要避免的。本文主要讲述了FPGA中的亚稳态问题,可以帮助…...

Leetcode86. 分隔链表
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。 你应当 保留 两个分区中每个节点的初始相对位置。 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台…...

如何处理 Flink 作业中的数据倾斜问题?
分析&回答 什么是数据倾斜? 由于数据分布不均匀,造成数据大量的集中到一点,造成数据热点。 举例:一个 Flink 作业包含 200 个 Task 节点,其中有 199 个节点可以在很短的时间内完成计算。但是有一个节点执行时间…...
cobbler自动化安装CentOS、windows和ubuntu
环境介绍 同时玩cobbler3.3和cobbler2.8.5 cobbler3.3 系统CentOS8.3 VMware虚拟机 桥接到物理网络 IP: 192.168.1.33 cobbler2.8.5 系统CentOS7.9 VMWare虚拟机 桥接到物理网络 IP:192.168.1.33 安装cobbler3.3 yum源修改 cat /etc/yum.repo.d/Cento…...

springcloud3 GateWay章节-Nacos+gateway动态路由负载均衡4
一 工程结构 1.1 工程 1.2 搭建gatewayapi工程 1.pom文件 <dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>4.13</version><scope>test</scope></dependency><!--gateway--&g…...

RESTful API 面试必问
RESTful API是一种基于 HTTP 协议的 API 设计风格,它提供了一组规范和约束,使得客户端(如 Web 应用程序、移动应用等)和服务端之间的通信更加清晰、简洁和易于理解。 RESTful API 的设计原则 使用 HTTP 协议:RESTful …...

软件机器人助力行政审批局优化网约车业务流程,推动审批业务数字化转型
随着社会的进步和发展,行政审批业务逐渐趋向于智能化和自动化。近日,某市行政审批局在市场准入窗口引入博为小帮软件机器人大幅度提升了网约车办理业务的效率,创新了原有的业务模式。 软件机器人以其自动化、智能化的特性,优化了网…...
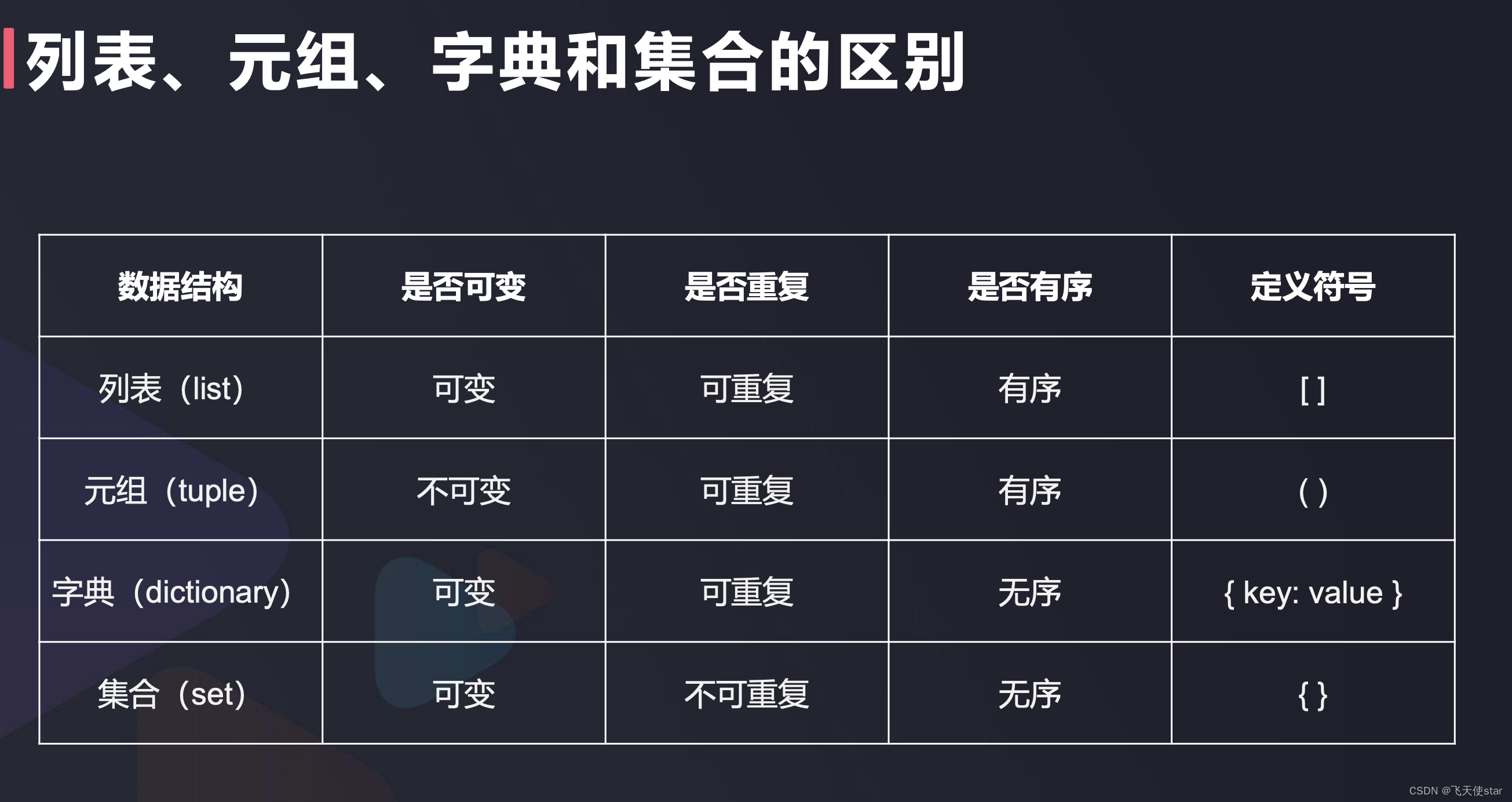
飞天使-python的字符串转义字符元组字典等
文章目录 基础语法数据类型python的字符串运算符输入和输出 数据结构列表与元组字典与集合 参考文档 基础语法 数据类型 数值型 ,整数 浮点型 布尔型, 真假, 假范围 字符型 类型转换python的字符串 了解转义字符一些基本的运算 \ 比如一行…...

stm32 uart dma方式接收不定长度字符
一般处理: stm32 uart使用dma接收时,会有自己的数据流中断,数据流中断会调用HAL_UART_RxCpltCallback。但是数据流中断只会在HAL_UART_Receive_DMA函数指定的buffer满时才会触发。 接收不定长度字符,需要和uart的UART_IT_IDLE结…...

SciencePub学术 | Elsevier出版社SCIEEI征稿中
SciencePub学术刊源推荐:Elsevier出版社SCIE&EI征稿中!信息如下,录满为止: 一、期刊概况: 计算机科学类SCI-01 【期刊简介】6.5-7.0,JCR1区,中科院2区; 【检索情况】正刊,SC…...
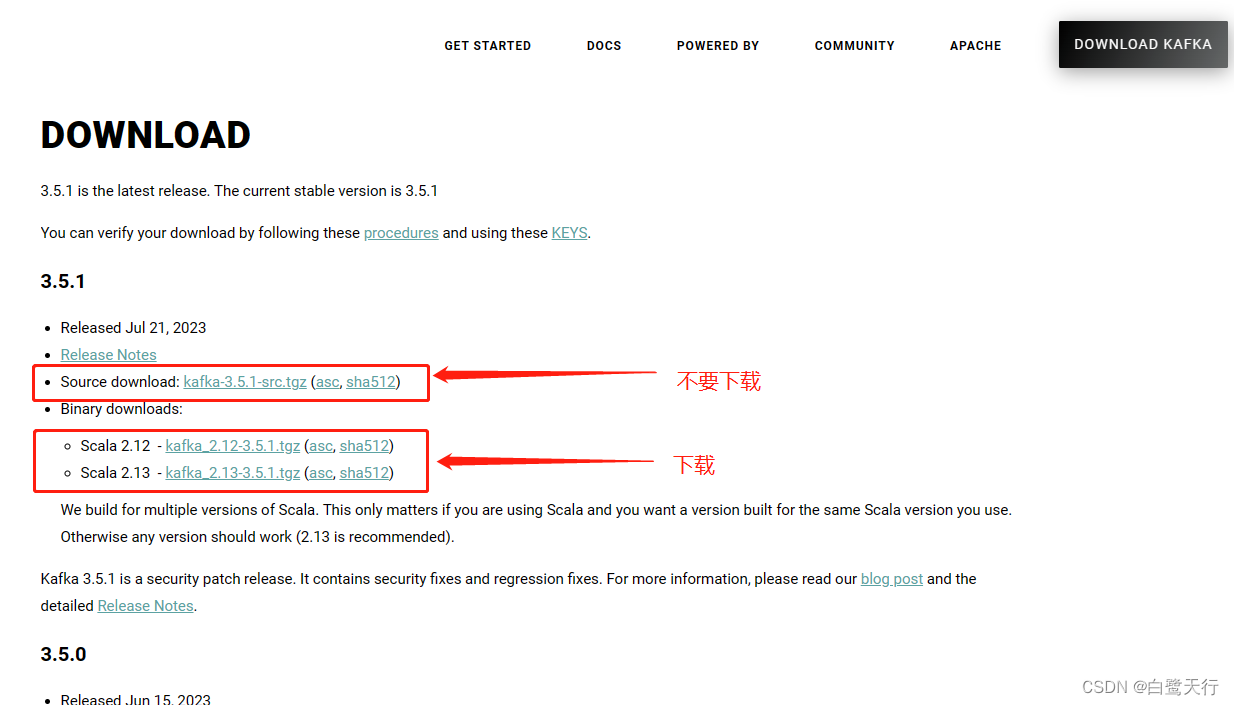
PHP小白搭建Kafka环境以及初步使用rdkafka
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、安装java(Kafka必须安装java,因为kafka依赖java核心)二、安装以及配置Kafka、zookeeper1.下载Kafka(无需下载…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
