2023年高教社杯数学建模思路 - 案例:ID3-决策树分类算法
文章目录
- 0 赛题思路
- 1 算法介绍
- 2 FP树表示法
- 3 构建FP树
- 4 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 算法介绍
FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,他与Apriori算法一样也是用来挖掘频繁项集的,不过不同的是,FP-Tree算法是Apriori算法的优化处理,他解决了Apriori算法在过程中会产生大量的候选集的问题,而FP-Tree算法则是发现频繁模式而不产生候选集。但是频繁模式挖掘出来后,产生关联规则的步骤还是和Apriori是一样的。
常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FP-growth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。
FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。
2 FP树表示法
FP树通过逐个读入事务,并把事务映射到FP树中的一条路径来构造。由于不同的事务可能会有若干个相同的项,因此它们的路径可能部分重叠。路径相互重叠越多,使用FP树结构获得的压缩效果越好;如果FP树足够小,能够存放在内存中,就可以直接从这个内存中的结构提取频繁项集,而不必重复地扫描存放在硬盘上的数据。
一颗FP树如下图所示:
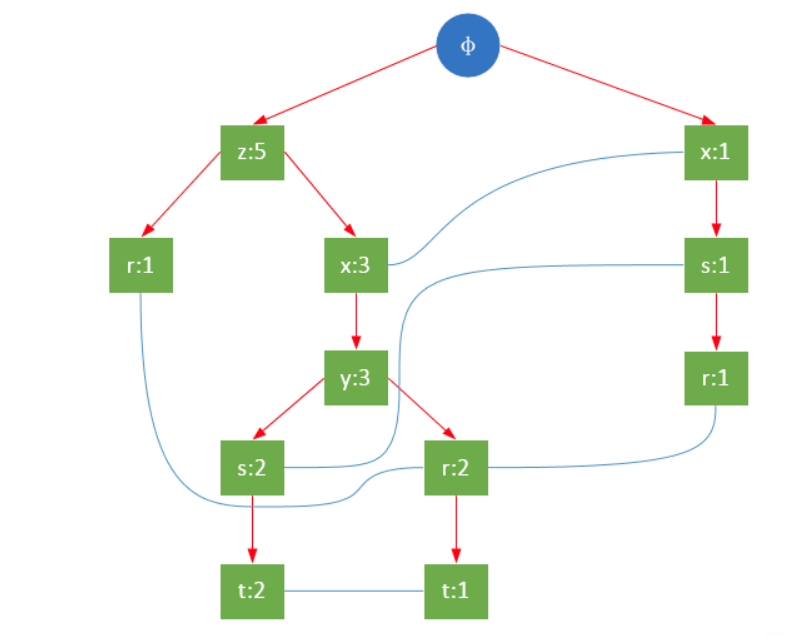
通常,FP树的大小比未压缩的数据小,因为数据的事务常常共享一些共同项,在最好的情况下,所有的事务都具有相同的项集,FP树只包含一条节点路径;当每个事务都具有唯一项集时,导致最坏情况发生,由于事务不包含任何共同项,FP树的大小实际上与原数据的大小一样。
FP树的根节点用φ表示,其余节点包括一个数据项和该数据项在本路径上的支持度;每条路径都是一条训练数据中满足最小支持度的数据项集;FP树还将所有相同项连接成链表,上图中用蓝色连线表示。
为了快速访问树中的相同项,还需要维护一个连接具有相同项的节点的指针列表(headTable),每个列表元素包括:数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针。
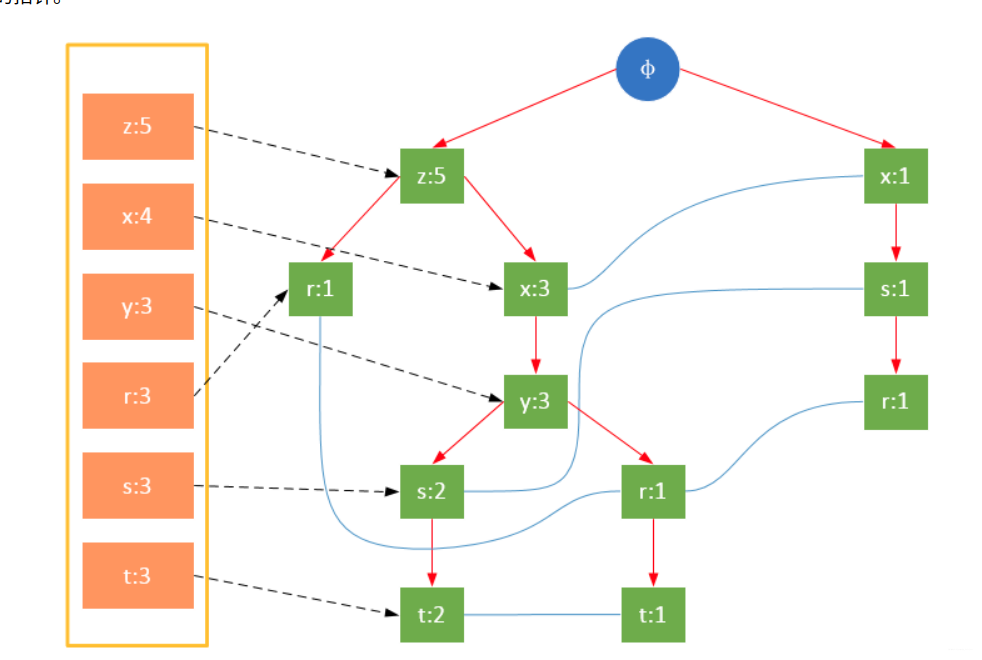
3 构建FP树
现在有如下数据:
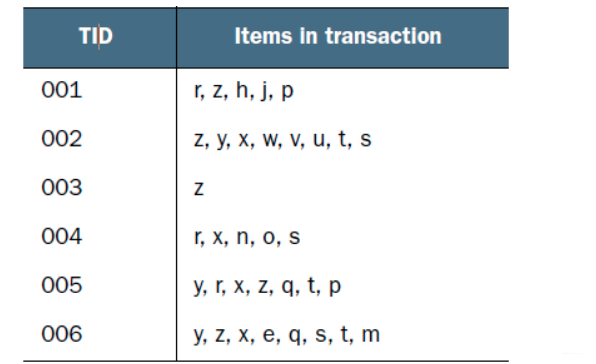
FP-growth算法需要对原始训练集扫描两遍以构建FP树。
第一次扫描,过滤掉所有不满足最小支持度的项;对于满足最小支持度的项,按照全局最小支持度排序,在此基础上,为了处理方便,也可以按照项的关键字再次排序。
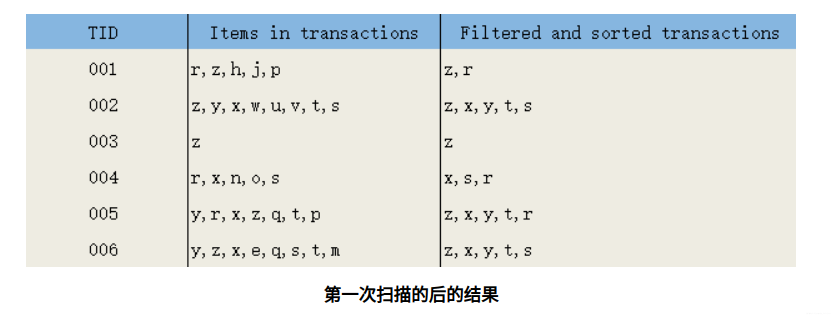
第二次扫描,构造FP树。
参与扫描的是过滤后的数据,如果某个数据项是第一次遇到,则创建该节点,并在headTable中添加一个指向该节点的指针;否则按路径找到该项对应的节点,修改节点信息。具体过程如下所示:
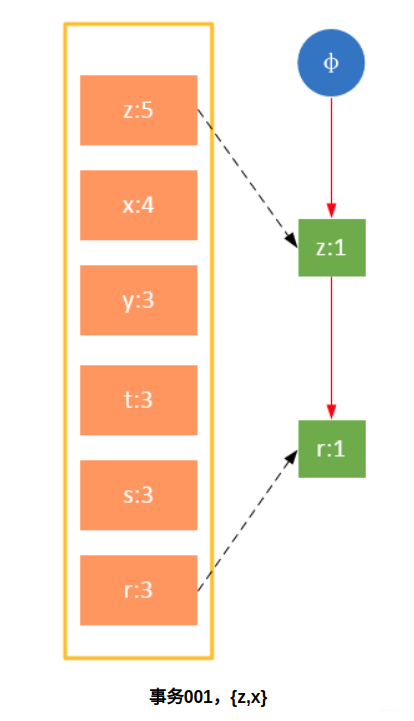
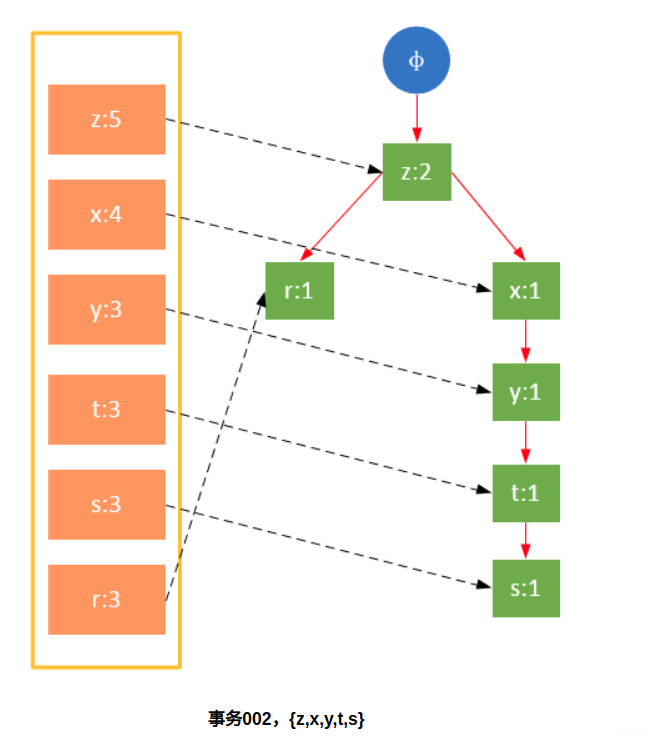
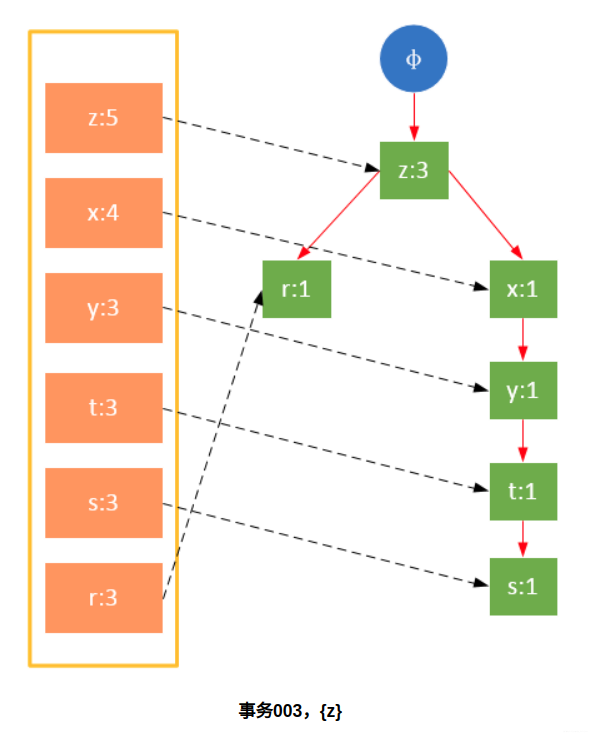
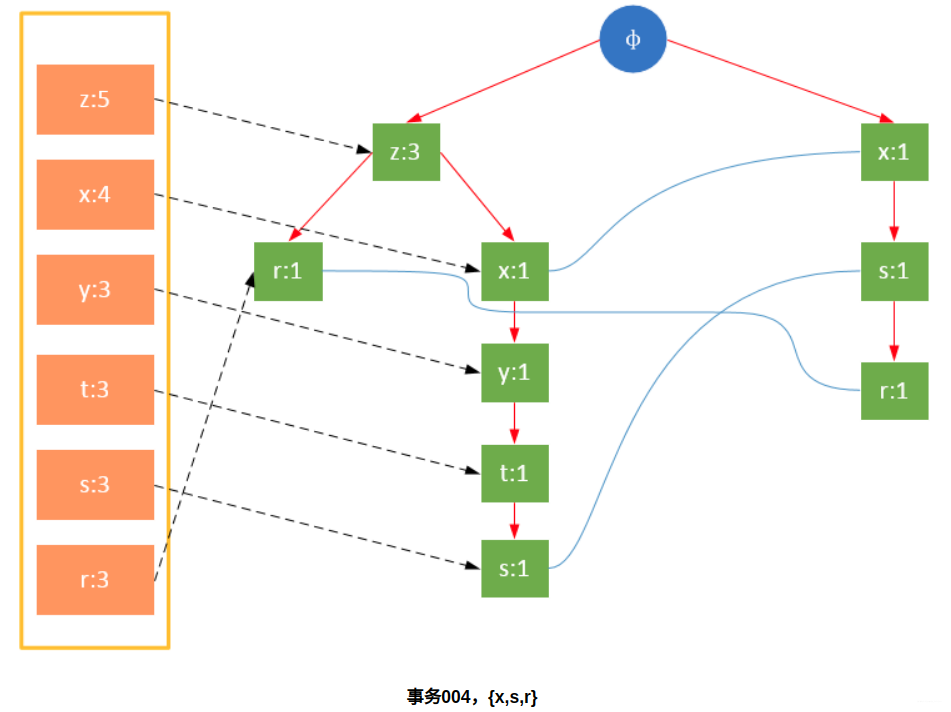
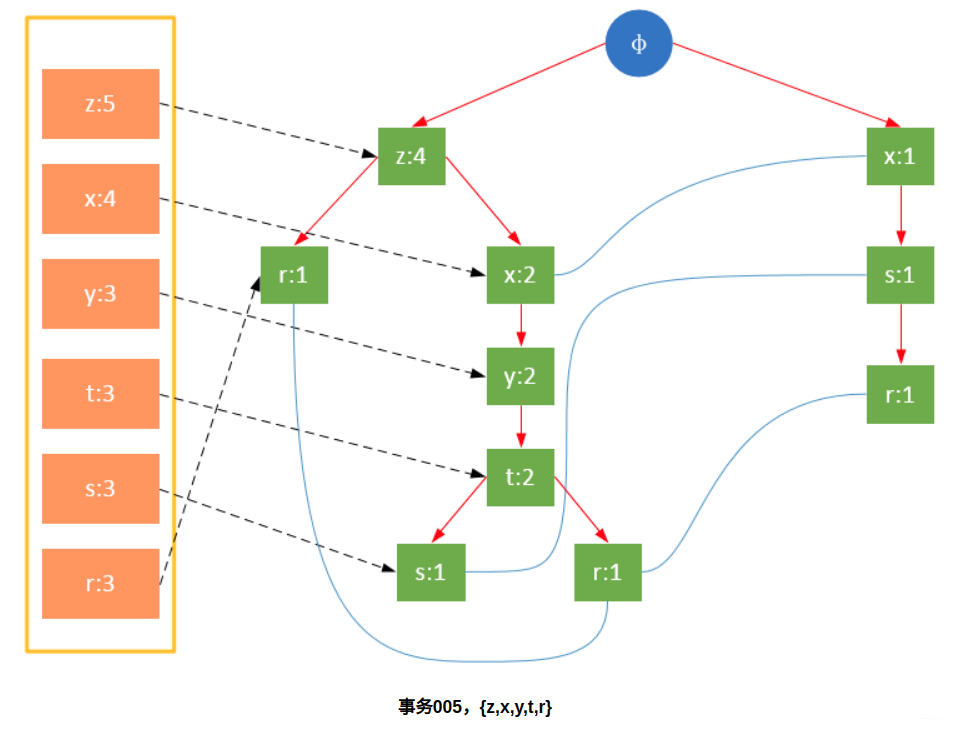
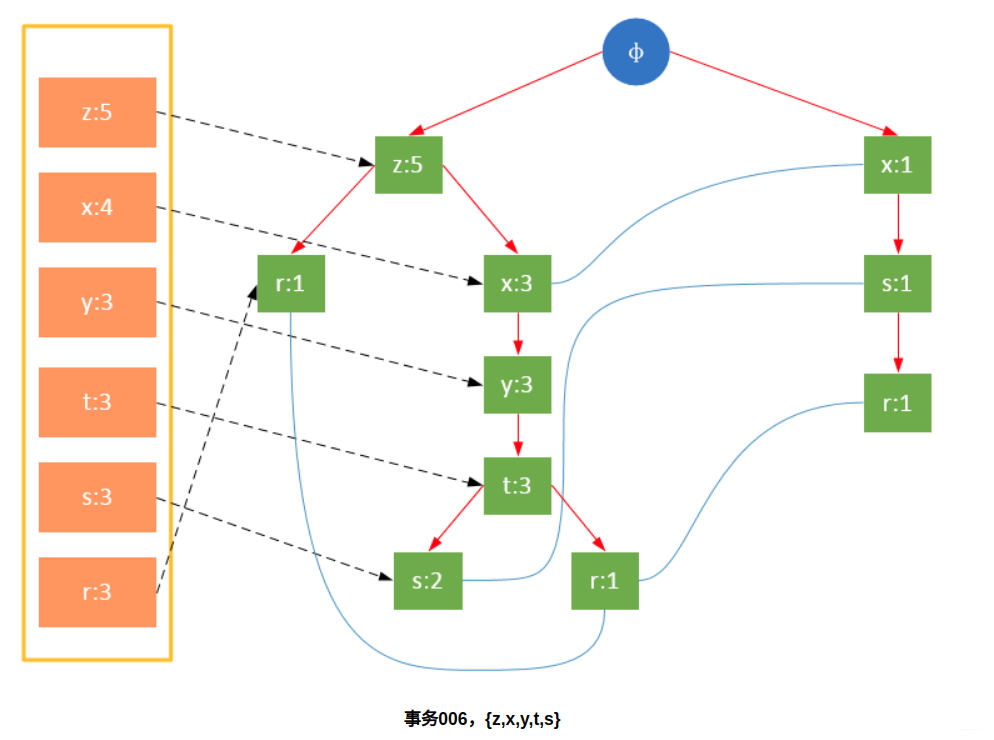
从上面可以看出,headTable并不是随着FPTree一起创建,而是在第一次扫描时就已经创建完毕,在创建FPTree时只需要将指针指向相应节点即可。从事务004开始,需要创建节点间的连接,使不同路径上的相同项连接成链表。
4 实现代码
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDatdef createInitSet(dataSet):retDict = {}for trans in dataSet:fset = frozenset(trans)retDict.setdefault(fset, 0)retDict[fset] += 1return retDictclass treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccurself.nodeLink = Noneself.parent = parentNodeself.children = {}def inc(self, numOccur):self.count += numOccurdef disp(self, ind=1):print(' ' * ind, self.name, ' ', self.count)for child in self.children.values():child.disp(ind + 1)def createTree(dataSet, minSup=1):headerTable = {}#此一次遍历数据集, 记录每个数据项的支持度for trans in dataSet:for item in trans:headerTable[item] = headerTable.get(item, 0) + 1#根据最小支持度过滤lessThanMinsup = list(filter(lambda k:headerTable[k] < minSup, headerTable.keys()))for k in lessThanMinsup: del(headerTable[k])freqItemSet = set(headerTable.keys())#如果所有数据都不满足最小支持度,返回None, Noneif len(freqItemSet) == 0:return None, Nonefor k in headerTable:headerTable[k] = [headerTable[k], None]retTree = treeNode('φ', 1, None)#第二次遍历数据集,构建fp-treefor tranSet, count in dataSet.items():#根据最小支持度处理一条训练样本,key:样本中的一个样例,value:该样例的的全局支持度localD = {}for item in tranSet:if item in freqItemSet:localD[item] = headerTable[item][0]if len(localD) > 0:#根据全局频繁项对每个事务中的数据进行排序,等价于 order by p[1] desc, p[0] descorderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: (p[1],p[0]), reverse=True)]updateTree(orderedItems, retTree, headerTable, count)return retTree, headerTabledef updateTree(items, inTree, headerTable, count):if items[0] in inTree.children: # check if orderedItems[0] in retTree.childreninTree.children[items[0]].inc(count) # incrament countelse: # add items[0] to inTree.childreninTree.children[items[0]] = treeNode(items[0], count, inTree)if headerTable[items[0]][1] == None: # update header tableheaderTable[items[0]][1] = inTree.children[items[0]]else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]])if len(items) > 1: # call updateTree() with remaining ordered itemsupdateTree(items[1:], inTree.children[items[0]], headerTable, count)def updateHeader(nodeToTest, targetNode): # this version does not use recursionwhile (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list!nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNodesimpDat = loadSimpDat()
dictDat = createInitSet(simpDat)
myFPTree,myheader = createTree(dictDat, 3)
myFPTree.disp()
上面的代码在第一次扫描后并没有将每条训练数据过滤后的项排序,而是将排序放在了第二次扫描时,这可以简化代码的复杂度。
控制台信息:

建模资料
资料分享: 最强建模资料


相关文章:

2023年高教社杯数学建模思路 - 案例:ID3-决策树分类算法
文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模…...

POJ 3273 Monthly Expense 二分
我们对每个月花费的最小花费进行二分,对于每一次二分的值mid,计算能花的月份数量,如果月份数量小于等于m,我们就不断的缩小mid,直到找到月份数量小于等于m 与 月份数量大于m的临界值,取最后一次满足条件的m…...
图论(基础)
知识: 顶点,边 | 权,度数 1.图的种类: 有向图 | 无向图 有环 | 无环 联通性 基础1:图的存储(主要是邻接矩阵和邻接表) 例一:B3643 图的存储 - 洛谷 | 计算机科学教育新生态 (…...

docker的运行原理
Docker 是一个开源的容器化技术,它能够让开发者将应用及其依赖打包到一个轻量级的、可移植的容器中,这个容器可以在几乎任何机器上一致地运行。要了解 Docker 的运行原理,我们首先要理解以下几个核心概念: 容器 (Container): 容器是一个轻量级的、独立的、可执行的软件包,…...
vue自定义键盘
<template><div class"mark" click"isOver"></div><div class"mycar"><div class"mycar_list"><div class"mycar_list_con"><p class"mycar_list_p">车牌号</p>…...
k8s 安装 kubernetes安装教程 虚拟机安装k8s centos7安装k8s kuberadmin安装k8s k8s工具安装 k8s安装前配置参数
k8s采用master, node1, node2 。三台虚拟机安装的一主两从,机器已提前安装好docker。下面是机器配置,k8s安装过程,以及出现的问题与解决方法 虚拟机全部采用静态ip, master 30机器, node1 31机器, node2 32机器 机器ip 192.168.164.30 # ma…...

2023年高教社杯数学建模思路 - 案例:感知机原理剖析及实现
文章目录 1 感知机的直观理解2 感知机的数学角度3 代码实现 4 建模资料 # 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 感知机的直观理解 感知机应该属于机器学习算法中最简单的一种算法,其…...
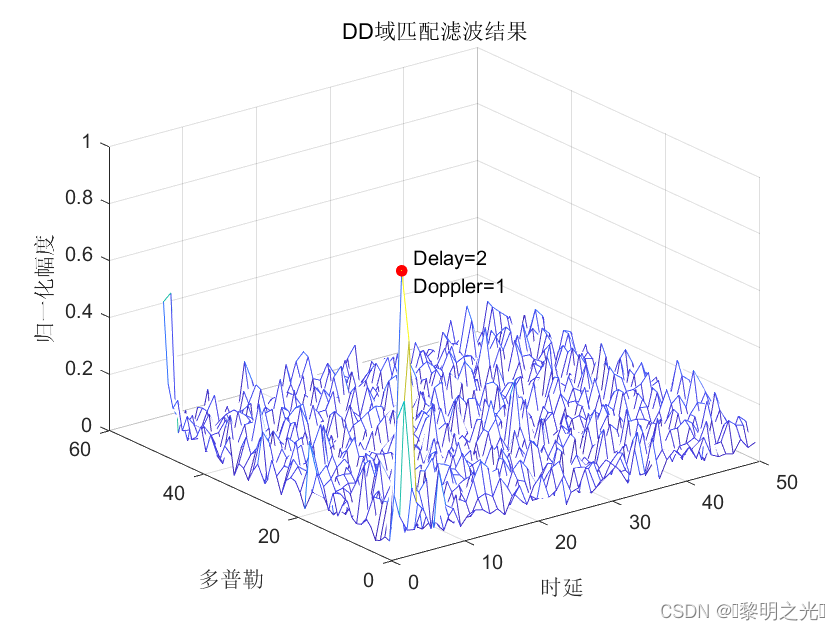
OTFS-ISAC雷达部分最新进展(含matlab仿真+USRP验证)
OTFS基带参数设置 我将使用带宽为80MHz的OTFS波形进行设计,对应参数如下: matlab Tx仿真 Tx导频Tx功率密度谱 帧结构我使用的是经典嵌入导频帧结构,Tx信号波形的带宽从右图可以看出约为80Mhz USRP验证 测试环境 无人机位于1m处 Rx导频Rx…...
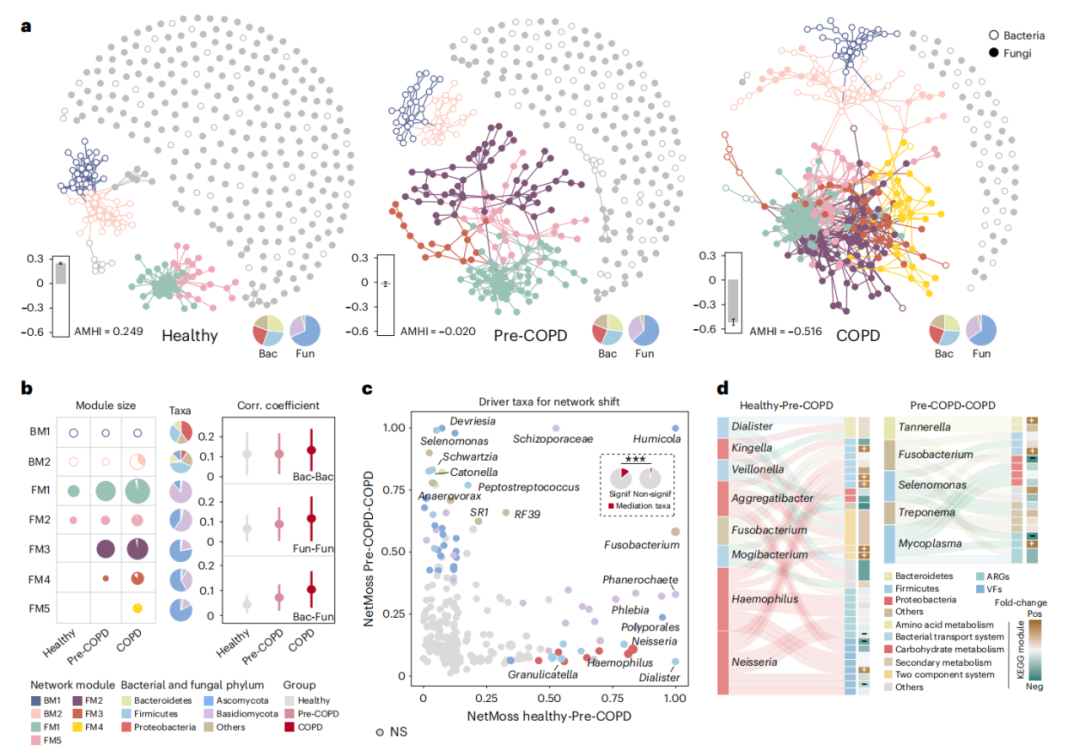
Cell | 超深度宏基因组!复原消失的肠道微生物
期刊:Cell IF:64.5 (Q1) 发表时间:2023.6 研究背景 不同的生活方式会影响微生物组组成,但目前微生物组的研究严重偏向于西方工业化人群,其中工业化人群的特点是微生物群多样性较低。为了理解工…...

Centos7 设置代理方法
针对上面变量的设置方法: 1、在/etc/profile文件 2、在~/.bashrc 3、在~/.zshrc 4、在/etc/profile.d/文件夹下新建一个文件xxx.sh 写入如下配置: export proxy"http://192.168.5.14:8118" export http_proxy$proxy export https_proxy$pro…...
)
Android versions (Android 版本)
Android versions (Android 版本) All Android releases https://developer.android.com/about/versions Android 1.0 G1 Android 1.5 Cupcake Android 1.6 Donut Android 2.0 Eclair Android 2.2 Froyo Android 2.3 Gingerbread Android 3.0 Honeycomb Android 4.0 Ic…...
LNMP 平台搭建(四十)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 搭建LNMP 一、安装Nginx 二、安装Mysql 三、安装PHP 四、部署应用 前言 LNMP平台指的是将Linux、Nginx、MySQL和PHP(或者其他的编程语言,如…...

pcie 6.0/7.0相对pcie 5.0的变化有哪些?
引言 话说,小编在CSDN博客跟客服机器人聊天,突然看到有个搜索热搜“pcie最全科普贴”。小编有点似曾相识呀,我就好奇点击了一下,没想到几年前写的帖子在CSDN又火了一把。 说到这里,顺带给自己打个广告哈~ …...

百度Apollo:自动驾驶技术的未来应用之路
文章目录 前言一、城市交通二、出行体验三、环境保护四、未来前景总结 前言 随着科技的不断进步,自动驾驶技术正逐渐成为现实,颠覆着我们的出行方式。作为中国领先的自动驾驶平台,百度Apollo以其卓越的技术和开放的合作精神,正在…...

C++之std::distance应用实例(一百八十八)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

中国建筑出版传媒许少辉八一新书乡村振兴战略下传统村落文化旅游设计日
中国建筑出版传媒许少辉八一新书乡村振兴战略下传统村落文化旅游设计日...
基于java Swing 和 mysql实现的购物管理系统(源码+数据库+说明文档+运行指导视频)
一、项目简介 本项目是一套基于java Swing 和 mysql实现的购物管理系统,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Java学习者。 包含:项目源码、项目文档、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过…...

2023.9 - java - static 关键字
static关键字主要和Java的内存管理有关。我们可以将static关键字与变量,方法,代码块一起使用。static关键字属于该类,而不是该类的实例。 static关键字可以修饰: 变量(也称为类变量)方法(也称…...

SpringCloud学习笔记(十二)_Zipkin全链路监控
Zipkin是SpringCloud官方推荐的一款分布式链路监控的组件,使用它我们可以得知每一个请求所经过的节点以及耗时等信息,并且它对代码无任何侵入,我们先来看一下Zipkin给我们提供的UI界面都是提供了哪些信息。 如何使用Zipkin 虽然在SpringBoot…...
Java 多线程系列Ⅱ(线程安全)
线程安全 一、线程不安全线程不安全的原因: 二、线程不安全案例与解决方案1、修改共享资源synchronized 使用synchronized 特性 2、内存可见性Java内存模型(JMM)内存可见性问题 3、指令重排列4、synchronized 和 volatile5、拓展知识…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
