当前位置： 首页 > news >正文

【3.Vue子组件调用父组件方法】

news 2026/2/9 2:42:26

1.概述

使用组件建抛出事件的方式来调用父组件的方法，不直接用this.$parent.function的方法，当然这种方式是可以的。

2.代码实现

2.1 父组件代码

父组件写一个方法给子组件调用

  // 设备点击事件// equipId:设备id// leftValue:left值// topValue:top值chileEquipClick(equipId, leftValue, topValue) {// 先关闭再打开this.clickEquipId = ""; // 清空idthis.inforDivShow = false;this.inforDivLeft = leftValue;this.inforDivTop = topValue;},

父组件在引入子组件的地方声明子组件抛出来的方法

<!--equipClick 就是子组件里面的方法名 --><equipLine01 @equipClick="chileEquipClick"></equipLine01>

2.2 子组件代码

子组件的方法 等同于 this.$parent.equipClick

 // 设备点击事件equipClick(item) {// this.$parent.equipClick(item.id, item.leftValue, item.topValue);// 抛出事件给父组件// item.id 设备id// item.leftValue left值// item.topValue top值this.$emit("equipClick", item.id, item.leftValue, item.topValue);},

相关文章：

【3.Vue子组件调用父组件方法】

1.概述 使用组件建抛出事件的方式来调用父组件的方法&#xff0c;不直接用this.$parent.function的方法&#xff0c;当然这种方式是可以的。 2.代码实现 2.1 父组件代码 父组件写一个方法给子组件调用 // 设备点击事件// equipId:设备id// leftValue:left值// topValue:top…...

编程日记 2023/9/2 16:09:40

算法系列-876-求链表的中间节点

求链表中间节点&#xff0c;如果有两个中间节点取后面那个 链表定义 // lc codestart /*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val val; }* ListNode(…...

编程日记 2023/9/2 16:08:39

h5 ws 客户端 监听ws服务器广播的信息

<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>AI智能写作</title><!-- Bootstrap CSS --><meta charset"utf-8"><meta name"viewport" content"widt…...

编程日记 2023/9/2 16:07:37

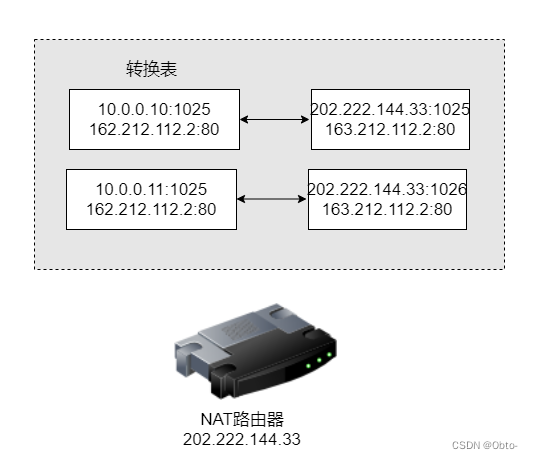
网络基础之重中之重

目录 IP协议 ​编辑 基本概念&#xff1a; 协议头格式&#xff1a; ​编辑 网段划分 DHCP &#xff1a; CIDR&#xff1a; 特殊的IP地址&#xff1a; IP地址的数量限制&#xff1a; 私有IP和公网IP 路由 路由的过程&#xff1a; 数据链路层 认识以太网&#x…...

编程日记 2023/9/2 16:06:35

HarmonyOS应用开发者-----基础认证试题及答案

HarmonyOS应用开发者基础认证试题及答案 试题会不定时刷新，本试题仅供大家学习参考 【判断题】 2.5/2.5 所有使用@Component修饰的自定义组件都支持onPageShow，onBackPress和onPageHide生命周期函数。 正确(True)错误(False) 回答正确【判断题】 2.5/2.5 在Column和Row容器组…...

编程日记 2023/9/2 16:05:34

C++：string并非以0作为结束符，c_str和data的返回却包含结束符0

C语言中使用char数组保存字符串时，是以字符为0或者\0作为字符串的结束符标志的。 所以一个char str[10]的数组只能合法的保存9个字符(因为最后还要加一个结束符)。 #include <cstring> #include <iostream>using namespace std;int main() {char str[10] ="…...

编程日记 2023/9/2 16:04:33

ChatGPT插件的优缺点

虽然西弗吉尼亚大学的研究人员看到了最新的官方ChatGPT插件——名为“代码解释器”&#xff08; Code Interpreter&#xff09;的教育应用潜力&#xff0c;但他们也发现&#xff0c;对于使用计算方法处理针对癌症和遗传疾病的定向治疗的生物数据的科学家来说&#xff0c;这款插…...

编程日记 2023/9/2 16:03:31

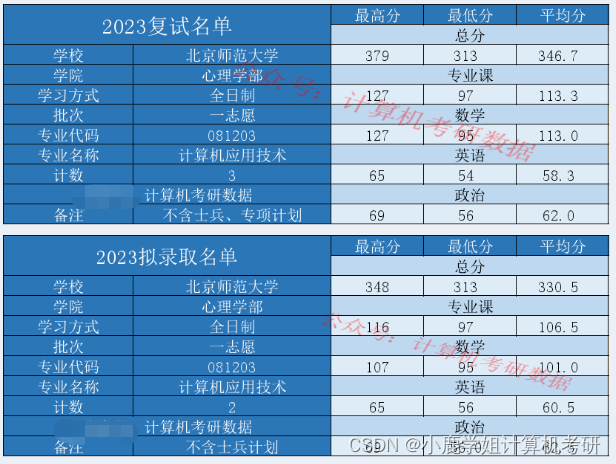
北京985学校，交叉学科考英一数三408

北京师范大学(B) 考研难度&#xff08;☆☆☆&#xff09; 内容&#xff1a;23考情概况&#xff08;拟录取和复试分析&#xff09;、院校概况、23专业目录、23复试详情、各专业考情分析、各科目考情分析。 正文1096字&#xff0c;预计阅读&#xff1a;3分钟 2023考情概况 北…...

编程日记 2023/9/2 16:02:29

ChatGPT 总结前端HTML, JS, Echarts都包含哪些内容

AIGC ChatGPT ，BI商业智能， 可视化Tableau, PowerBI, FineReport， 数据库Mysql Oracle， Office， Python ，ETL Excel 2021 实操，函数，图表，大屏可视化 案例实战 http://t.csdn.cn/zBytu...

编程日记 2023/9/2 16:01:28

企业架构LNMP学习笔记1

项目开发流程&#xff1a; 公司老板或者产品经理&#xff0c;根据市场调查&#xff0c;决定开发一整套互联网产品。 互动社交电商用户论坛&#xff08;BBS&#xff09; 产品决策 &#xff08;老板产品UI设计&#xff09; 业务实施、代码开发 程序开发人员 前端开发&#x…...

编程日记 2023/9/2 16:00:27

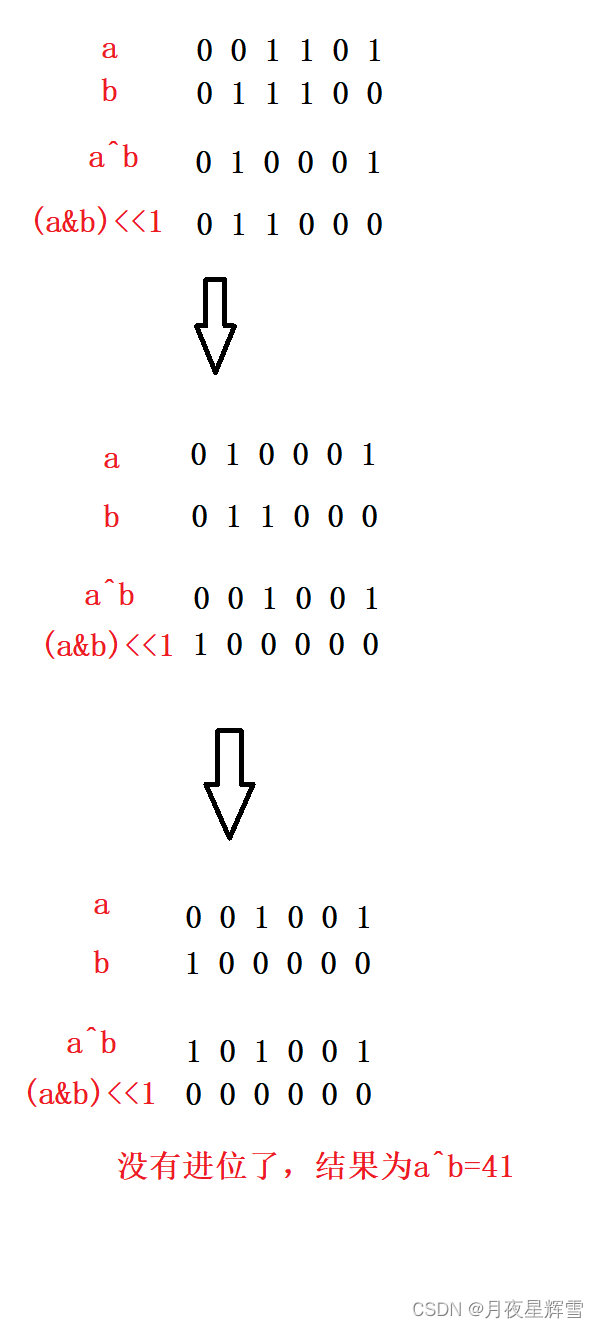
【位运算】leetcode371：两整数之和

一.题目描述 两整数之和 二.思路分析 题目要求我们实现两整数相加&#xff0c;但是不能使用加号&#xff0c;应该立马想到是用位运算来解决问题。之前说过&#xff0c;异或就是“无进位相加”&#xff0c;故本题可以先将两数异或&#xff0c;然后想办法让得到的结果进位即可。…...

编程日记 2023/9/2 15:59:26

【爬虫小知识】如何利用爬虫爬网页——python爬虫

前言 网络时代的到来&#xff0c;给我们提供了海量的信息资源&#xff0c;但是&#xff0c;想要获取这些信息&#xff0c;手动一个一个网页进行查找&#xff0c;无疑是一项繁琐且效率低下的工作。这时&#xff0c;爬虫技术的出现&#xff0c;为我们提供了一种高效的方式去获取…...

编程日记 2023/9/2 15:58:25

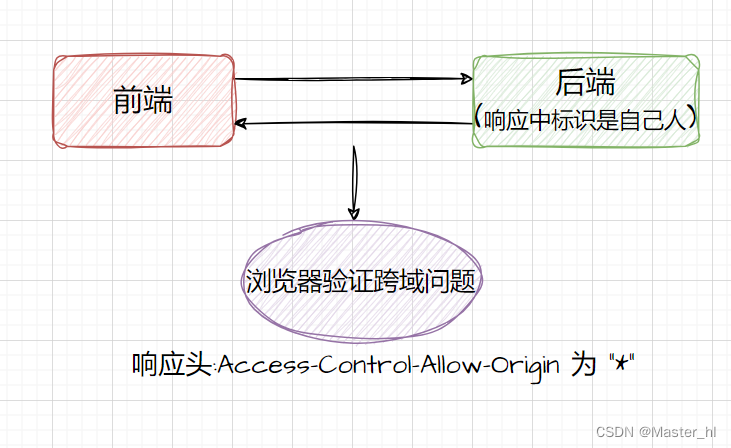
什么是跨域问题 ？Spring MVC 如何解决跨域问题 ？Spring Boot 如何解决跨域问题 ？

目录 1. 什么是跨域问题 &#xff1f; 2. Spring MVC 如何解决跨域问题 &#xff1f; 3. Spring Boot 如何解决跨域问题 &#xff1f; 1. 什么是跨域问题 &#xff1f; 跨域问题指的是不同站点之间&#xff0c;使用 ajax 无法相互调用的问题。 跨域问题的 3 种情况&#x…...

编程日记 2023/9/2 15:57:24

线性代数的学习和整理17：向量空间的基，自然基，基变换等（未完成）

目录 3 向量空间的基&#xff1a;矩阵的基础/轴 3.1 从颜色RGB说起 3.2 附属知识 3.3 什么样的向量可以做基&#xff1f; 3.4 基的分类 3.1.1 不同空间的基---向量组的数量可能不同 3.1.2 自然基 3.1.3 正交基 3.1.4 标准正交基 3.1.5 基和向量/矩阵 3.1.6 基变换 …...

编程日记 2023/9/2 15:56:23

Java中支持分库分表的框架/组件/中间件简介

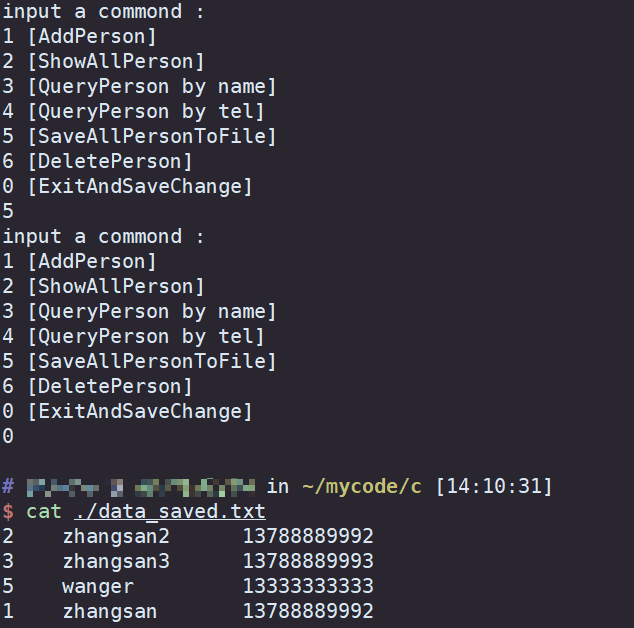
文章目录 1 sharding-jdbc2 TSharding3 Atlas4 Cobar5 MyCAT6 TDDL7 Vitess 列举一些比较常见的&#xff0c;简单介绍一下&#xff1a; sharding-jdbc&#xff08;当当&#xff09; TSharding&#xff08;蘑菇街&#xff09; Atlas&#xff08;奇虎360&#xff09; Cobar&#…...

编程日记 2023/9/2 15:55:22

7.2 项目2 学生通讯录管理：文本文件增删改查（C 版本）(自顶向下设计+断点调试) (A)

C自学精简教程 目录(必读) 该作业是 作业 学生通讯录管理&#xff1a;文本文件增删改查&#xff08;C版本&#xff09; 的C 语言版本。 具体的作业题目描述&#xff0c;要求&#xff0c;可以参考 学生通讯录管理&#xff1a;文本文件增删改查&#xff08;C版本&#xff09;。…...

编程日记 2023/9/2 15:54:21

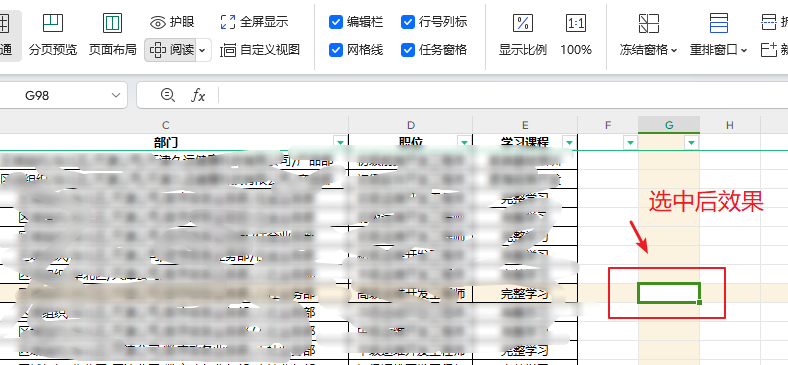
excel怎么设置任意选一个单元格纵横竖横都有颜色

有时excel表格内容过多的时候&#xff0c;我们通过excel设置任意选一个单元格纵横&#xff0c;竖横背景颜色&#xff0c;这样会更加具有辨识度。设置方式截图如下 设置成功后&#xff0c;预览的效果图...

编程日记 2023/9/2 15:53:20

期货-股票交易规则

交易时间 港股&#xff1a;9:00~9:20 集合竞价&#xff0c;9:3012:00&#xff0c;13:0016:00 持续交易&#xff0c;16:00~16:10 随机收市竞价沪股&#xff1a;9:00~9:25 集合竞价&#xff0c;9:3011:30&#xff0c;13:0015:00 持续交易&#xff0c;11:30~12:00 交易申报深股&a…...

编程日记 2023/9/2 15:52:19

Makefile一些语法

ifneq($(filter true,$(xxx)), )的含义 filter 是过滤的意思&#xff0c;它的原型是&#xff1a;$(filter PATTERN…,TEXT)&#xff0c; 意义为&#xff1a;过滤掉字串“TEXT”中所有不符合模式“PATTERN”的单词&#xff0c;保留所有符合此模式的单词做返回值。 结合前面的if…...

编程日记 2023/9/2 15:51:16

0基础可以转行编程行业么

在2022年分行业门类分岗位就业人员年平均工资中&#xff0c;信息传输、软件和信息技术服务业的薪资遥遥领先其他行业&#xff0c;为全国平均薪资水平的 1.78 倍&#xff0c;远超第二名金融行业&#xff0c;其年增长率在9.4%&#xff0c;并成为年收入首个过20 万门槛的行业&…...

编程日记 2023/9/2 15:50:15

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖

在前面的练习中&#xff0c;每个页面需要使用ref&#xff0c;onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入&#xff0c;需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

编程新知 2025/9/14 18:41:15

Rust 异步编程

Rust 异步编程 引言 Rust 是一种系统编程语言，以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天，异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

编程新知 2025/11/17 18:58:56

【JavaSE】绘图与事件入门学习笔记

-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角&#xff0c;以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向&#xff0c;距离坐标原点x个像素;第二个是y坐标&#xff0c;表示当前位置为垂直方向&#xff0c;距离坐标原点y个像素。 坐标体系-像素 …...

编程新知 2025/12/19 20:46:15

【JavaWeb】Docker项目部署

引言 之前学习了Linux操作系统的常见命令&#xff0c;在Linux上安装软件&#xff0c;以及如何在Linux上部署一个单体项目&#xff0c;大多数同学都会有相同的感受&#xff0c;那就是麻烦。 核心体现在三点&#xff1a; 命令太多了&#xff0c;记不住 软件安装包名字复杂&…...

编程新知 2026/2/4 16:07:02

3-11单元格区域边界定位(End属性)学习笔记

返回一个Range 对象&#xff0c;只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意&#xff1a;它移动的位置必须是相连的有内容的单元格…...

编程新知 2026/1/20 19:15:45

Redis的发布订阅模式与专业的 MQ（如 Kafka, RabbitMQ）相比，优缺点是什么？适用于哪些场景？

Redis 的发布订阅&#xff08;Pub/Sub&#xff09;模式与专业的 MQ&#xff08;Message Queue&#xff09;如 Kafka、RabbitMQ 进行比较&#xff0c;核心的权衡点在于&#xff1a;简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

编程新知 2025/12/4 2:32:37

LLMs 系列实操科普（1）

写在前面&#xff1a; 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容&#xff0c;原视频时长 ~130 分钟&#xff0c;以实操演示主流的一些 LLMs 的使用&#xff0c;由于涉及到实操&#xff0c;实际上并不适合以文字整理&#xff0c;但还是决定尽量整理一份笔…...

编程新知 2026/1/31 11:35:24

JS手写代码篇----使用Promise封装AJAX请求

15、使用Promise封装AJAX请求 promise就有reject和resolve了&#xff0c;就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

编程新知 2025/12/16 3:15:21

Python学习(8) ----- Python的类与对象

Python 中的类&#xff08;Class&#xff09;与对象&#xff08;Object&#xff09;是面向对象编程&#xff08;OOP&#xff09;的核心。我们可以通过“类是模板&#xff0c;对象是实例”来理解它们的关系。 &#x1f9f1; 一句话理解&#xff1a; 类就像“图纸”&#xff0c;对…...

编程新知 2025/10/23 12:11:37

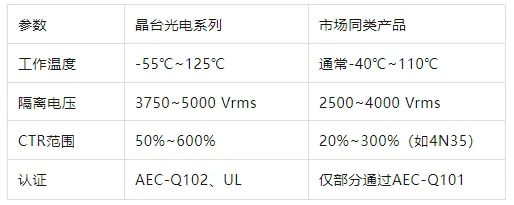
高抗扰度汽车光耦合器的特性

晶台光电推出的125℃光耦合器系列产品&#xff08;包括KL357NU、KL3H7U和KL817U&#xff09;&#xff0c;专为高温环境下的汽车应用设计&#xff0c;具备以下核心优势和技术特点&#xff1a; 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计&#xff0c;确保在…...

编程新知 2026/2/5 4:25:30