【蓝桥杯集训·每日一题】AcWing 1497. 树的遍历
文章目录
- 一、题目
- 1、原题链接
- 2、题目描述
- 二、解题报告
- 1、思路分析
- 2、时间复杂度
- 3、代码详解
- 三、知识风暴
- 递归
一、题目
1、原题链接
1497. 树的遍历
2、题目描述
一个二叉树,树中每个节点的权值互不相同。
现在给出它的后序遍历和中序遍历,请你输出它的 层序遍历。
输入格式
第一行包含整数 N,表示二叉树的节点数。
第二行包含 N 个整数,表示二叉树的后序遍历。
第三行包含 N 个整数,表示二叉树的中序遍历。
输出格式
输出一行 N 个整数,表示二叉树的层序遍历。
数据范围
1≤N≤30,官方并未给出各节点权值的取值范围,为方便起见,在本网站范围取为 1∼N。输入样例:
7 2 3 1 5 7 6 4 1 2 3 4 5 6 7输出样例:
4 1 6 3 5 7 2
二、解题报告
1、思路分析
思路来源:y总讲解视频
y总yyds
预备知识:
- 前序遍历:根左右(先遍历根结点,然后遍历左孩子、右孩子,下面类似)。
- 中序遍历:左根右。
- 后序遍历:左右根。
- 层次遍历:从根结点开始,依次从左往右遍历每层的结点。
(1)我们可以通过后序遍历的最后一个一个结点来确定整棵树的根结点,
(2)根据根结点的位置我们可以在中序遍历中得知整棵树的左右子树,分别包含哪些结点。
(3)递归地对左右子树进行上述操作,直到后序遍历中子树大小为空,这样就可以依次将每层的结点找到,然后把每层的结点记录下来,输出即可。
2、时间复杂度
时间复杂度O(n)
3、代码详解
用vector记录每层结点然后输出
#include <iostream>
#include <vector>
using namespace std;
const int N=35;
int n;
int h[N],z[N],p[N]; //h[]存储树的后序遍历,z[]存储树的中序遍历,p[i]存储值为i的数在中序遍历中的下标
vector<int> c[N]; //c[i]存储第i层的层序遍历
void build(int hl,int hr,int zl,int zr,int d){ //传入后序遍历的起点和终点、中序遍历的起点和终点,当前的层数if(hl>hr) return ;int val=h[hr]; //根结点的值c[d].push_back(val); //将根结点加入第d层的层序遍历中int idx=p[val]; //根结点在中序遍历中的下标build(hl,hl+idx-1-zl,zl,idx-1,d+1); //递归遍历左子树build(hl+idx-zl,hr-1,idx+1,zr,d+1); //递归遍历右子树
}
int main(){cin>>n;for(int i=0;i<n;i++){cin>>h[i];}for(int i=0;i<n;i++){cin>>z[i];}for(int i=0;i<n;i++){p[z[i]]=i;}build(0,n-1,0,n-1,0);for(int i=0;i<n;i++){for(int j=0;j<c[i].size();j++){cout<<c[i][j]<<' ';}}return 0;
}
建树,然后bfs输出层序遍历
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N=35;
int n;
int h[N],z[N],p[N]; //h[]存储树的后序遍历,z[]存储树的中序遍历,p[i]存储值为i的数在中序遍历中的下标
int l[N],r[N]; //l[]存储每个结点的左孩子,r[]存储每个结点的右孩子
//建树,返回根结点
int build(int hl,int hr,int zl,int zr,int d){ //传入后序遍历的起点和终点、中序遍历的起点和终点,当前的层数if(hl>hr) return 0; //如果子树为空,返回0int val=h[hr]; //根结点的值int idx=p[val]; //根结点在中序遍历中的下标l[val]=build(hl,hl+idx-1-zl,zl,idx-1,d+1); //递归遍历左子树,找到左子树的根结点r[val]=build(hl+idx-zl,hr-1,idx+1,zr,d+1); //递归遍历右子树,找到右子树的根结点return val;
}
//bfs输出层序遍历
void bfs(){queue<int> q;q.push(h[n-1]);while(q.size()){int t=q.front();q.pop();cout<<t<<' ';if(l[t]) q.push(l[t]);if(r[t]) q.push(r[t]);}
}
int main(){cin>>n;for(int i=0;i<n;i++){cin>>h[i];}for(int i=0;i<n;i++){cin>>z[i];}for(int i=0;i<n;i++){p[z[i]]=i;}build(0,n-1,0,n-1,0);bfs();return 0;
}
三、知识风暴
递归
- 递归是指函数直接或间接调用自己,是一种描述问题和解决问题的常用方法。
- 递归有两个基本要素:
- 边界条件:即确定递归到何时终止,也就是递归出口。
- 递归模式:即大问题是如何分解成小问题的,也就是递归体。
相关文章:

【蓝桥杯集训·每日一题】AcWing 1497. 树的遍历
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴递归一、题目 1、原题链接 1497. 树的遍历 2、题目描述 一个二叉树,树中每个节点的权值互不相同。 现在给出它的后序遍历和中序遍历,请你输出它的 …...

详解matplotlib的color配置
详解matplotlib的color配置 Matplotlib可识别的color格式 格式举例RGB或RGBA,由[0, 1]之间的浮点数组成的元组,分别代表红色、绿色、蓝色和透明度(0.1, 0.2, 0.5), (0.1, 0.2, 0.5, 0.3不区分大小写的十六进制RGB或RGBA字符串。‘#0f0f0f’, ‘#0f0f0f…...

Oracle删除表数据的三种方式
简介 oracle数据库mysql数据库都是如此 drop命令>truncate命令>delete命令,它们的执行方式、效率和结果各有不同。还是万年的student 学生表 自己可以建个尝试这玩一下。 drop命令 语句: drop table 表名; 理由:1、用drop删除表数据&…...
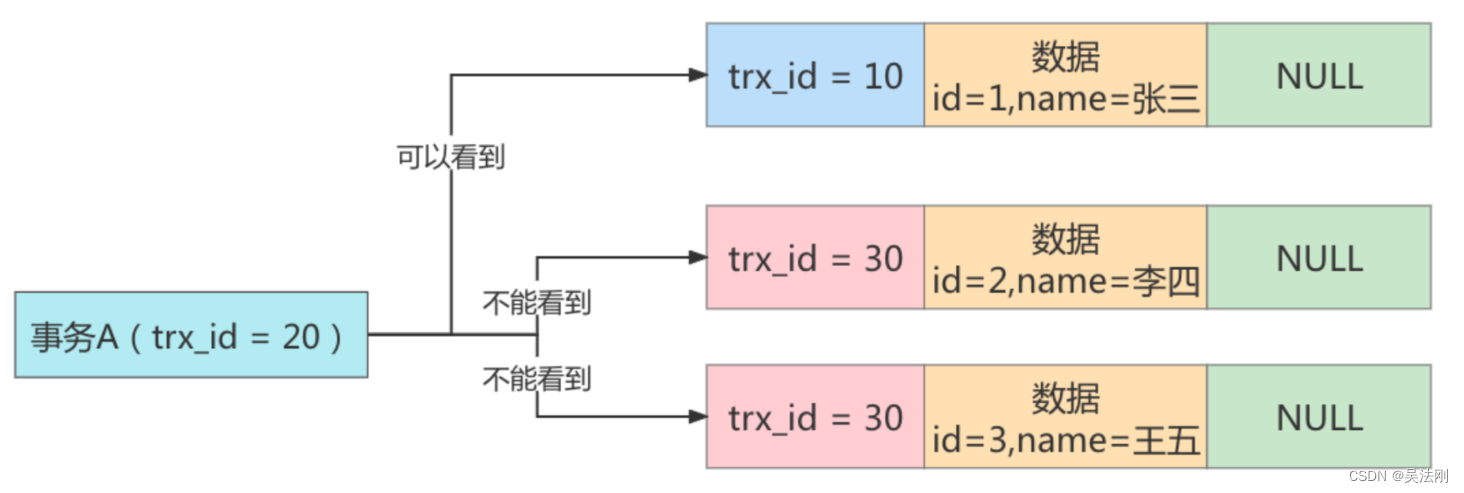
第 16 章_多版本并发控制
第 16 章_多版本并发控制 1. 什么是MVCC MVCC (Multiversion Concurrency Control),多版本并发控制。顾名思义,MVCC 是通过数据行的多个版本管理来实现数据库的并发控制。这项技术使得在InnoDB的事务隔离级别下执行一致性读操作…...

五种 IO 模型
文章目录操作系统和内存内核空间和用户空间应用程序的内核态和用户态网络 IO 和磁盘 IO简易的网络通信流程阻塞和非阻塞阻塞 IO 模型非阻塞 IO 模型IO 复用模型SelectPollEpoll小结信号驱动 IO 模型异步 IO 模型五种 IO 模型的对比IO 模型里的同步和异步5种 IO 模型分别是&…...

34-Golang中的结构体!!!
Golang中的结构体结构体和结构体变量(实例)的区别和联系结构体变量(实例)在内存中的布局如何声明结构体字段/属性注意事项和细节说明创建结构体实例的四种方式结构体使用细节结构体和结构体变量(实例)的区别和联系 1.结构体是自定义的数据类型,代表一类事物2.结构体…...

这6个视频剪辑素材库,你一定要知道~
推荐5个免费商用视频素材网站,建议收藏哦! 1、菜鸟图库 视频素材下载_mp4视频大全 - 菜鸟图库 网站素材量很大,有设计、图片、音频、视频等超多素材,大部分都能免费下载。视频素材都很高清,有自然、人物、科技、农业…...

RocketMQ WIN11 搭建
去官方下载 https://rocketmq.apache.org/zh/download/ 下载,博主下载的是 4.6.0 的版本,选择Binary版本 拓展 Source 下载:需要编译 Binary 下载:不需要编译 解压缩,运行 先解压缩环境变量中添加rocketMQ文件夹路…...
iPhone更换电池和屏幕后提醒非原厂配件的操作办法
---开局一张图,内容全靠编系列! 【图】 自从在iPhone系统iOS13开始支持原厂配件检测后,可以说苹果也动起了维修站商家利益的这块蛋糕。道理自然简单,卷嘛!全球汽车行业也不是靠卖新车才赚钱的,各种交通事故…...

chatGPT发布记录
发行说明(2 月 13 日)我们对 ChatGPT 进行了多项更新!这是新功能:我们更新了免费计划中 ChatGPT 模型的性能,以便为更多用户提供服务。根据用户反馈,我们现在默认让 Plus 用户使用更快的 ChatGPT 版本&…...
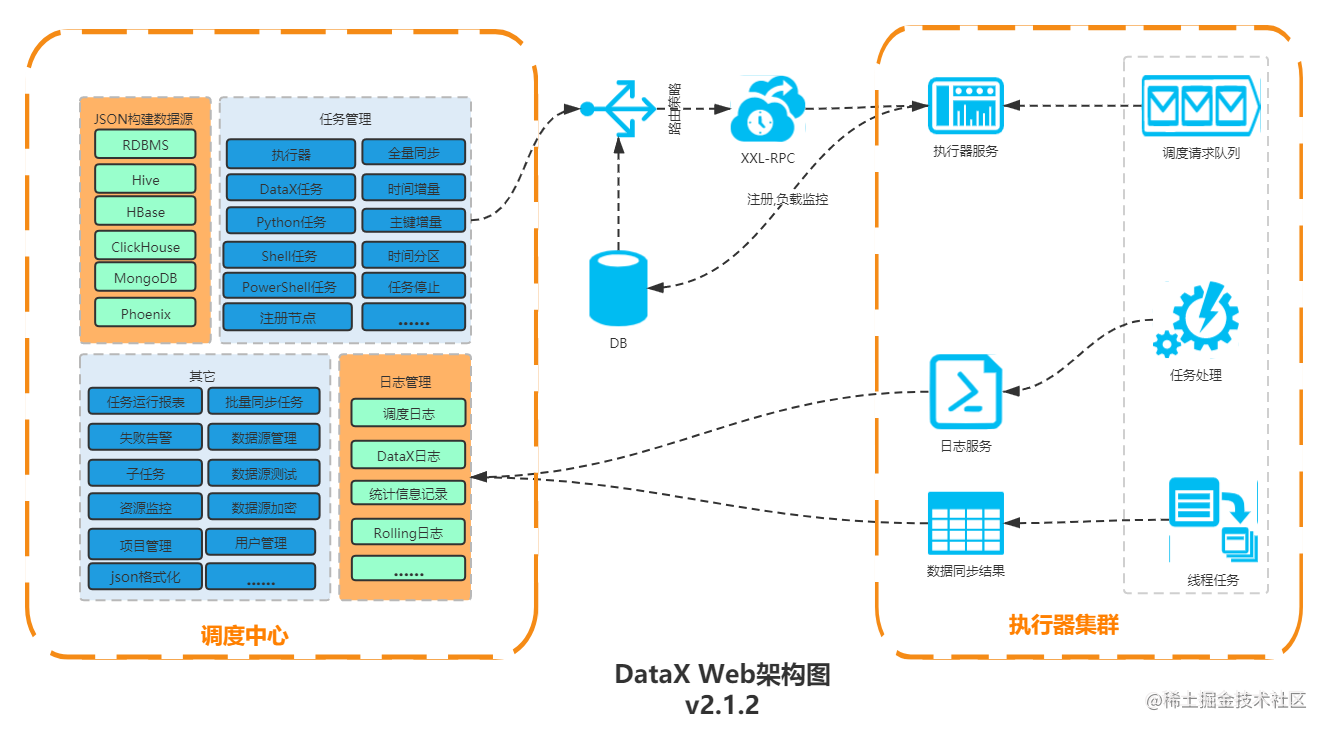
DataX及DataX-Web
大数据Hadoop之——数据同步工具DataX数据采集工具-DataX datax详细介绍及使用 一、概述 DataX 是阿里云DataWorks数据集成的开源版本,在阿里巴巴集团内被广泛使用的离线数据同步工具/平台。DataX 实现了包括 MySQL、Oracle、OceanBase、SqlServer、Postgre、HDFS、…...

数据结构与算法系列之kmp算法
什么是kmp算法 1.kmp算法是一种改进的字符串算法,其核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数已达到快速匹配的目的。 它主要实现作用的是 在 (主串)中找到 (匹配)字符串。 例 BF算法与k…...

算法分析详解
自古老的公元前1世纪开始,《周髀算经》就作为中国最古老的天文学和数学著作。 《周髀算经》采用最简便可行的方法确定天文历法,揭示日月星辰的运行规律,包括四季更替,气候变化,南北有极,昼夜相推的道理。为…...

东南大学自然辩证法概论期末总结
写在前面 作者:夏日 博客地址:https://blog.csdn.net/zss192 本文为2022年东南大学自然辩证法概论期末总结,内容为根据老师所发题纲综合多个资料总结得来 考试形式:从老师所发题纲,10个题目中选出4个,题…...

《爆肝整理》保姆级系列教程python接口自动化(二十)--token登录(详解)
简介 为了验证用户登录情况以及减轻服务器的压力,减少频繁的查询数据库,使服务器更加健壮。有些登录不是用 cookie 来验证的,是用 token 参数来判断是否登录。token 传参有两种一种是放在请求头里,本质上是跟 cookie 是一样的&…...
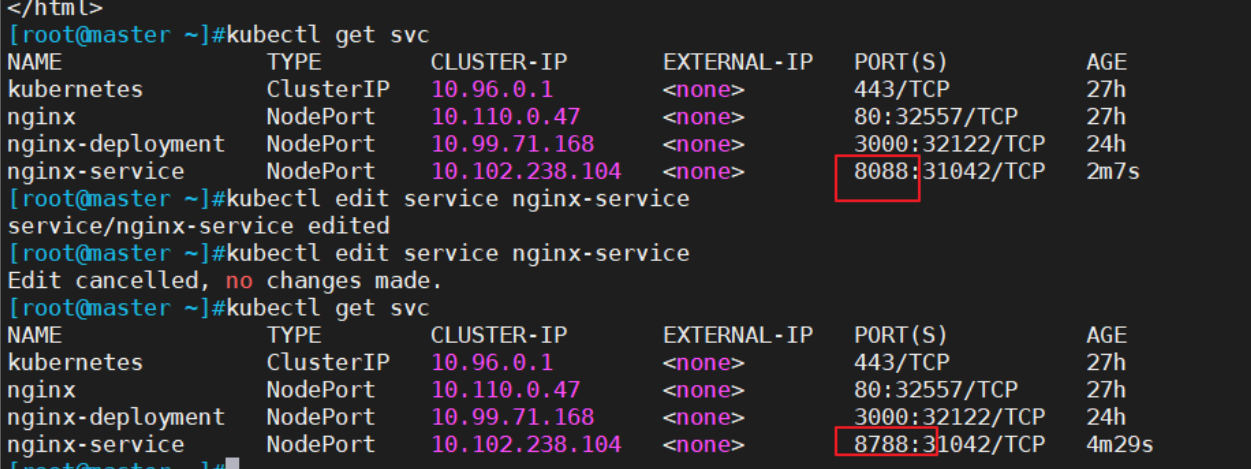
k8s种的kubectl命令
一.kubectl基本命令1.1 称述式资源管理的方法kubernetes集群管理集群资源的唯一入口是通过相应的方法调用apiserver的接口kubectl是官方的CLI命令行工具,用于与apiserver进行通信,将用户在命令行输入的命令,组织并转化为apiserver能识别的信息…...

数组(一)-- LeetCode[26][80] 删除有序数组中的重复元素
1 删除有序数组中的重复项 1.1 题目描述 给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。 由于在某些语言中不能改变数组的长度,…...
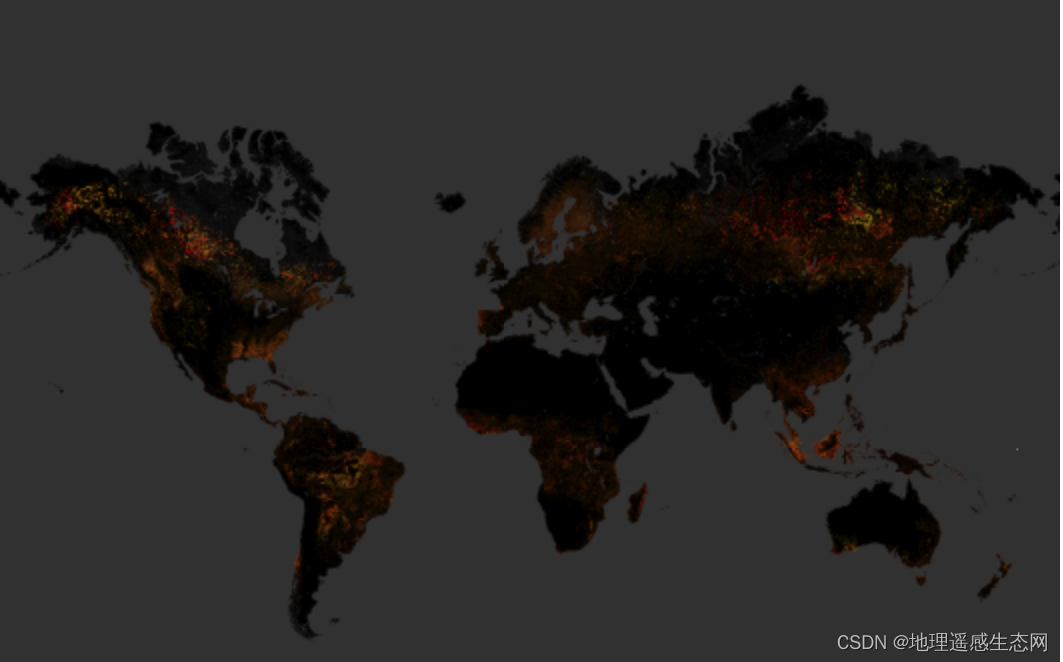
GEE学习笔记 六十三:新的地图图层ui.Map.CloudStorageLayer
在GEE中导出数据有一种方式是直接导出地图到Google Cloud Storage中,也就是Export.map.toCloudStorage(xxx),这种方式是将我们计算生成影像导出成为静态瓦片的格式存放在Google Cloud Storage中。我们可以在其他的前端程序比如OpenLayer、Mapbox GL JS等…...

ClickHouse 语法详解
ClickHouse有2类解析器:完整SQL解析器(递归式解析器),以及数据格式解析器(快速流式解析器) 除了 INSERT 查询,其它情况下仅使用完整SQL解析器。 INSERT查询会同时使用2种解析器:INSE…...
手把手教你将微信小程序放到git上
背景 首先,要创建一个自己的git仓库,这里默认大家都能够自己创建了git仓库了。如果不会创建仓库的话,百度一下,很容易就能够创建了!(后续,如有不知道在哪里,怎么创建仓库的话&#…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
