【css】css奇数、偶数、指定数选择器:
文章目录
- 一、简单数字序号写法:nth-child(number)
- 二、倍数写法:nth-child(an)
- 三、倍数分组匹配:nth-child(an+b) 与 :nth-child(an-b)
- 四、反向倍数分组匹配:nth-child(-an+b)
- 五、奇偶匹配:nth-child(odd) 与 :nth-child(even)
:nth-child(n)选择器匹配属于其父元素的第 N 个子元素,不论元素的类型
:nth-of-type(n)匹配同类型中的第n个同级兄弟元素
区别:
nth-child(n) : 匹配父元素中的第 n 个子元素,元素类型没有限制。
nth-of-type(n) : 匹配同类型中的第n个同级兄弟元素。
n可以是一个数字,一个关键字,或者一个公式,比如:nth-child(odd) 奇数 ,nth-child(even) 偶数。
nth-child和nth-of-type的不同之处就是查找元素的方式不同。前者是查找兄弟元素中某个绝对位置的元素,后者是查找同类型元素中某个绝对位置的元素。
相同:都是找到元素之后再与前面的选择符进行匹配,这里的匹配方式是一样的。
一、简单数字序号写法:nth-child(number)
:nth-child(number)直接匹配第number个元素。参数number必须为大于0的整数。
/* 把第3个LI的背景设为橙色 */
li:nth-child(3){background:orange;
}
二、倍数写法:nth-child(an)
:nth-child(an)匹配所有倍数为a的元素。其中参数an中的字母n不可缺省,它是倍数写法的标志,如3n、5n。
/* 把第3、第6、第9、…、所有3的倍数的LI的背景设为橙色 */
li:nth-child(3n){background:orange;
}
三、倍数分组匹配:nth-child(an+b) 与 :nth-child(an-b)
:nth-child(an+b) 与 :nth-child(an-b)先对元素进行分组,每组有a个,b为组内成员的序号,其中字母n和加号+不可缺省,位置不可调换,这是该写法的标志,其中a,b均为正整数或0。如3n+1、5n+1。但加号可以变为负号,此时匹配组内的第a-b个。(其实an前面也可以是负号,但留给下一部分讲。)
/* 匹配第1、第4、第7、…、每3个为一组的第1个LI*/
li:nth-child(3n+1){background:orange;
}/*匹配第5、第8、第11、…、从第5个开始每3个为一组的第1个LI */
li:nth-child(3n+5){background:orange;
}/*匹配第5-1=4、第10-1=9、…、第5的倍数减1个LI*/
li:nth-child(5n-1){background:orange;
}/*相当于(3n)*/
li:nth-child(3n±0){background:orange;
}/*相当于(3)*/
li:nth-child(±0n+3){background:orange;
}
四、反向倍数分组匹配:nth-child(-an+b)
:nth-child(-an+b)此处一负一正,均不可缺省,否则无意义。这时与:nth-child(an+1)相似,都是匹配第1个,但不同的是它是倒着算的,从第b个开始往回算,所以它所匹配的最多也不会超过b个。
/*匹配第8、第5和第2个LI*/
li:nth-child(-3n+8){background:orange;
}/*或(-n+8),匹配前8个(包括第8个)LI,这个较为实用点,用来限定前面N个匹配常会用到*/
li:nth-child(-1n+8){background:orange;
}
五、奇偶匹配:nth-child(odd) 与 :nth-child(even)
:nth-child(odd) 与 :nth-child(even)分别匹配序号为奇数与偶数的元素。奇数(odd)与(2n+1)结果一样;偶数(even)与(2n+0)及(2n)结果一样。
//(偶数行)
.table > tr:nth-child(even) > td {background-color: #ccc;
} //(奇数行)
.table > tr:nth-child(odd) > td {background-color: #ccc;
}
相关文章:

【css】css奇数、偶数、指定数选择器:
文章目录 一、简单数字序号写法:nth-child(number)二、倍数写法:nth-child(an)三、倍数分组匹配:nth-child(anb) 与 :nth-child(an-b)四、反向倍数分组匹配:nth-child(-anb)五、奇偶匹配:nth-child(odd) 与 :nth-child(even) :nth-child(n) 选择器匹配属于其父元素的第 N 个子元…...

三维数据Ply格式介绍与读取
三维数据Ply格式介绍与读取 PLY文件格式是在1990年代中期由斯坦福大学的一组研究人员开发的。它已经发展成为最广泛使用的3D数据文件格式之一。该文件格式有ASCII版本和二进制版本。在需要文件大小和处理效率的情况下,首选二进制版本。ASCII版本使得调试变得非常容易。在这里…...

内存管理方式
内存管理 一、C/C内存分布1、内存空间的介绍2、示例题目3、示例题目图解 二、C语言动态内存管理方式1、代码2、介绍 三、C内存管理方式1、概念2、代码3、代码所代表的意义 四、new和delete操作自定义类型1、代码2、运行结果3、特点 五、operator new与operator delete函数1、概…...

文心一言接入Promptulate,开发复杂LLM应用程序
简介 最近在尝试将文心一言的LLM能力接入Promptulate,故写了一篇博客记录一下,Promptulate 是 Promptulate AI 旗下的大语言模型自动化与应用开发框架,旨在帮助开发者通过更小的成本构建行业级的大模型应用,其包含了LLM领域应用层…...

TDengine函数大全-聚合函数
以下内容来自 TDengine 官方文档 及 GitHub 内容 。 以下所有示例基于 TDengine 3.1.0.3 TDengine函数大全 1.数学函数 2.字符串函数 3.转换函数 4.时间和日期函数 5.聚合函数 6.选择函数 7.时序数据库特有函数 8.系统函数 聚合函数 TDengine函数大全APERCENTILEAVGCOUNTELAPS…...
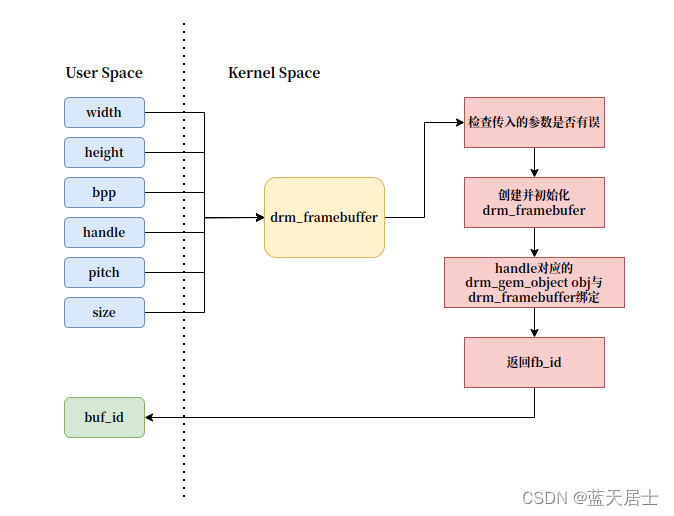
DRM全解析 —— ADD_FB(2)
接前一篇文章:DRM全解析 —— ADD_FB(1) 本文参考以下博文: DRM驱动(四)之ADD_FB 特此致谢! 上一回围绕libdrm与DRM在Linux内核中的接口: DRM_IOCTL_DEF(DRM_IOCTL_MODE_ADDFB, d…...

windows下docker compose方式挂载数据卷volume遇到的问题
例子一,windows 下docker desk top部署TDengine td-compose.yml version: 3 services:tdengine1:image: tdengine/tdengine:latestcontainer_name: tdengine1hostname: tdengine1ports:- 6030:6030- 6041:6041- 6043-6049:6043-6049- 6043-6049:6043-6049/udpresta…...
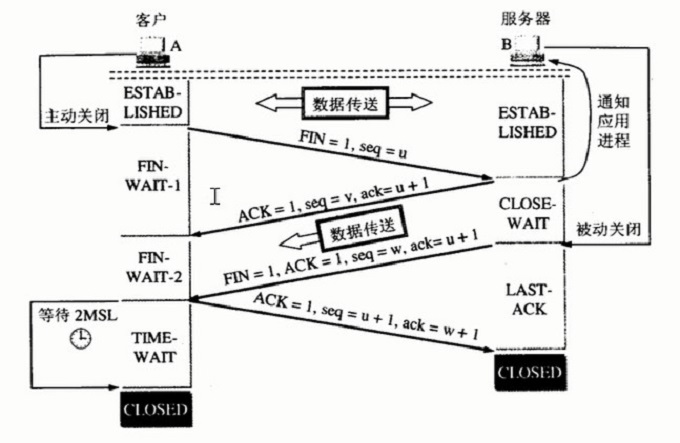
TCP三次握手四次挥手总结
目录 一、两种传输模式: 二、数据方向: 三、端口的作用: 四、端口类型: 五、三次握手: 六、四次断开 常见面试题 TCP(Transfer control protocol)传输控制协议 一、两种传输模式&#x…...

【0901作业】QTday3 对话框、发布软件、事件处理机制,使用文件相关操作完成记事本的保存功能、处理键盘事件完成圆形的移动
目录 一、思维导图 二、作业 2.1 使用文件相关操作完成记事本的保存功能 2.2 处理键盘事件完成圆形的移动 一、思维导图 二、作业 2.1 使用文件相关操作完成记事本的保存功能 void Widget::on_saveBtn_clicked() {QString filename QFileDialog::getSaveFileName(this,&…...
 NULL DEFAULT NULL报错【杭州多测师_王sir】)
mysql数据库运行sql:datetime(0) NULL DEFAULT NULL报错【杭州多测师_王sir】
一、错误信息 CREATE TABLE file (id varchar(32) CHARACTER SET utf8mb4 COLLATE utf8mb4_general_ci NOT NULL COMMENT 文件md5,name varchar(128) CHARACTER SET utf8mb4 COLLATE utf8mb4_general_ci NOT NULL,create_time datetime(0) NULL DEFAULT NULL,update_time date…...
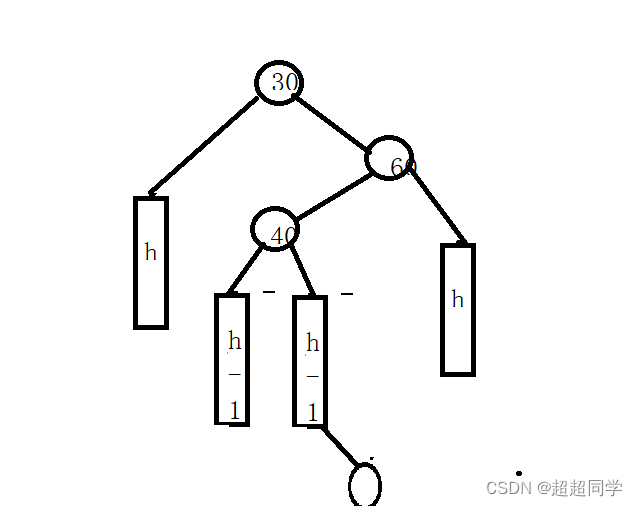
手撕二叉平衡树
今天给大家带来的是平衡树的代码实现,如下: #pragma once #include <iostream> #include <map> #include <set> #include <assert.h> #include <math.h> using namespace std; namespace cc {template<class K, clas…...
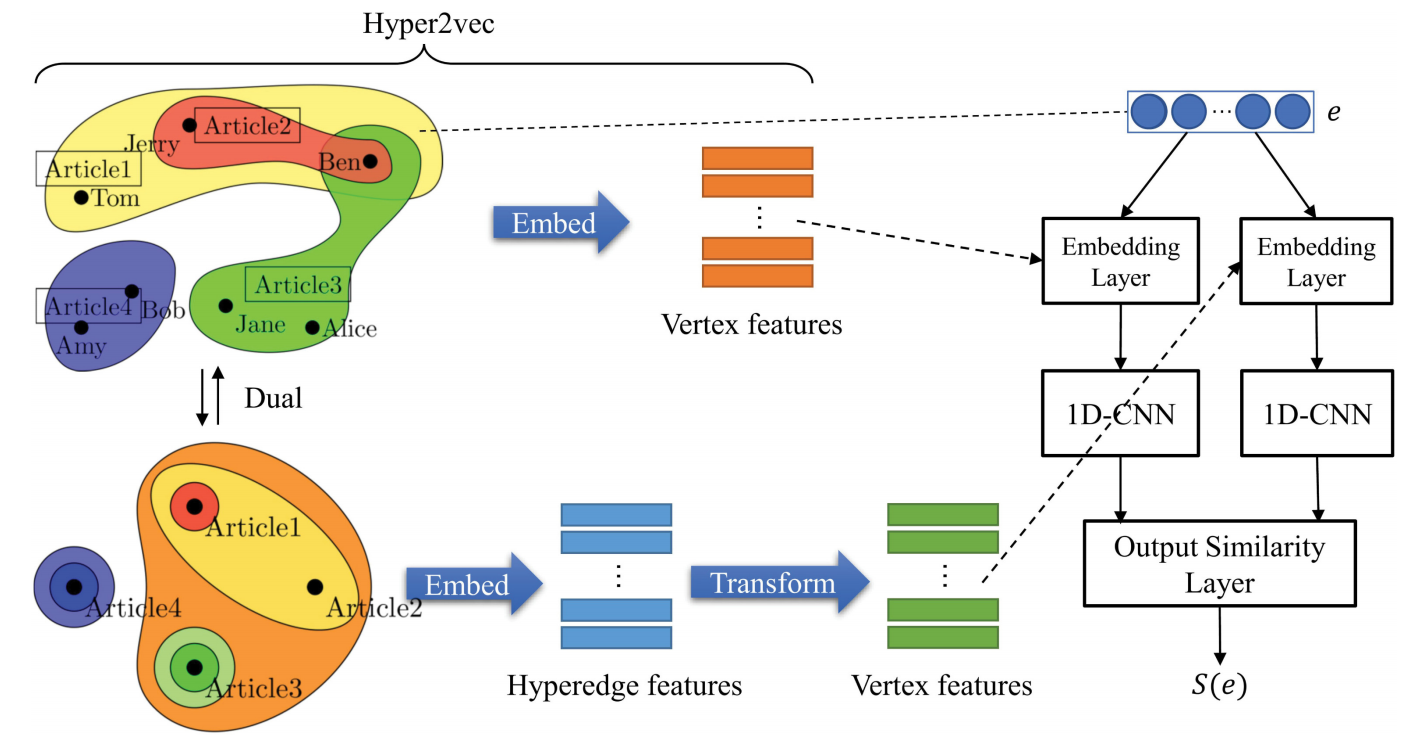
超图嵌入论文阅读1:对偶机制非均匀超网络嵌入
超图嵌入论文阅读1:对偶机制非均匀超网络嵌入 原文:Nonuniform Hyper-Network Embedding with Dual Mechanism ——TOIS(一区 CCF-A) 背景 超边:每条边可以连接不确定数量的顶点 我们关注超网络的两个属性࿱…...
Qt xml解析之QXmlStreamReader
文章目录 背景QXmlStreamReader简单介绍使用QXmlStreamReader添加头文件<QXmlStreamReader>toString()toInt()完整代码 背景 项目中遇到需要解析某个方法返回的xml字符串,奈何C/C中没有原生的方法可供调用,只能使用第三方库,搜了一圈资…...

Selenium基础 — CSS选择器定位大全
1、css属性定位 css选择器策略示例说明#id#telA选择id"telA"的所有元素。.class.telA选择 class"telA”的所有元素。[属性名属性值][nametelA]除了id和class属性,其他属性的定位格式[attribute][target]选择带有target 属性所有元素。**选择所有元素…...

vue3中keep-alive的使用及结合transition使用
正确用法 在组件中使用(这里结合了 transition 内置动画组件 ) <template><div class"layout clearfix"><router-view v-slot"{ Component, route }"><transition name"fade-transform" mode"…...

【提示工程】询问GPT返回Json结构数据
theme: orange 众所周知,我们可以通过构建的Prompt获取期望的内容,但是通常都是以自然语言返回的,假如我们想得到结构化的数据,比如Json,XML那么怎么办,这篇文章给你一个思路。 理所当然的想法 要实现询问大…...

CSS水平垂直居中方案
1 前言 水平居中、垂直居中是前端面试百问不厌的问题。其实现方案也是多种多样,常叫人头昏眼花。 水平方向可以认为是内联方向,垂直方向认为是块级方向。 2 内联元素的水平垂直居中 首先,常见内联元素有:a、span、em、b、stro…...
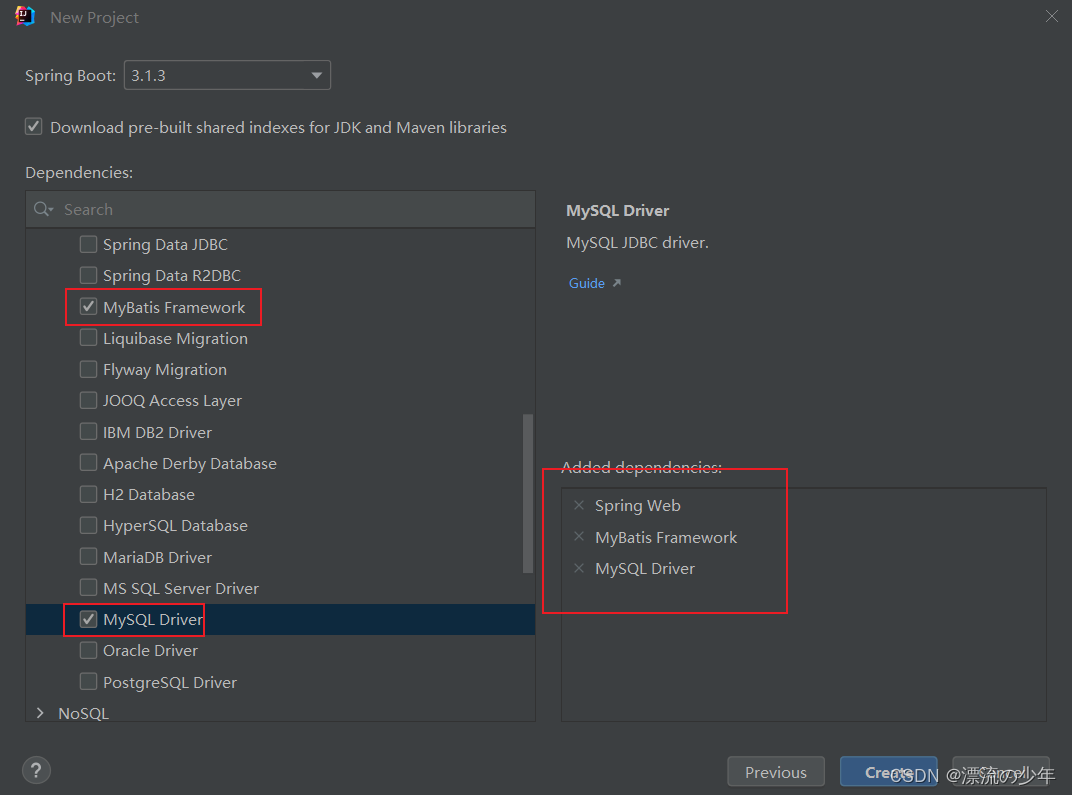
SpringBoot入门篇3 - 整合junit、整合mybatis、基于SpringBoot实现ssm整合
目录 1.整合JUnit Spring整合JUnit SpringBoot整合JUnit 测试类注解:SpringBootTest 作用:设置JUnit加载的SpringBoot启动类 2.整合mybatis ①使用spring initializr初始化项目的时候,添加依赖。 ②设置数据源application.yml spring:d…...
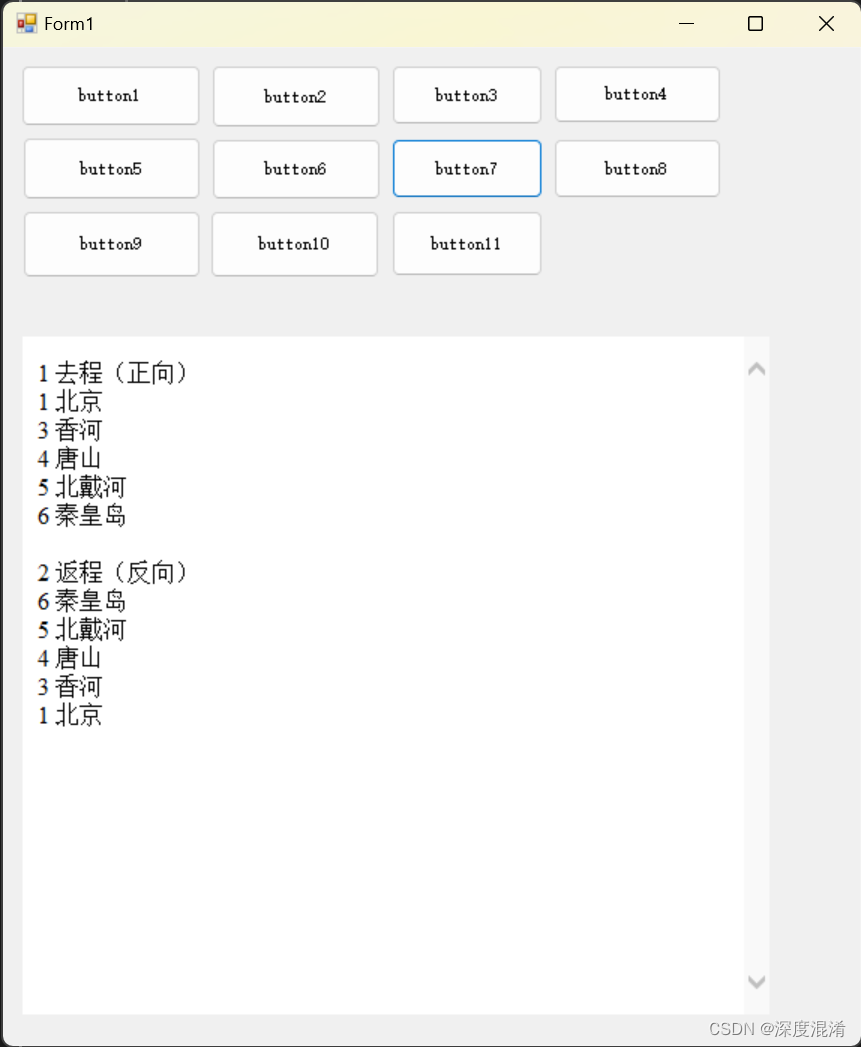
C#,《小白学程序》第七课:列表(List)应用之一“编制高铁车次信息表”
1 文本格式 /// <summary> /// 车站信息类 class /// </summary> public class Station { /// <summary> /// 编号 /// </summary> public int Id { get; set; } 0; /// <summary> /// 车站名 /// </summary>…...

周报/月报 Prompt
前言 用 AI 写好一份周报或月报。 文章目录 前言一、目的二、Prompt 设计原则三、模板 一、目的 简单的日程,扩写成一篇高质量的周报; 二、Prompt 设计原则 角色 目标 背景 要求 三、模板 内容生成模板 你是我的周报助手,根据我的工作…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...
