当前位置： 首页 > news >正文

【两周学会FPGA】从0到1学习紫光同创FPGA开发|盘古PGL22G开发板学习之数码管静态显示（四）

news 2026/2/11 3:23:37

  本原创教程由深圳市小眼睛科技有限公司创作，版权归本公司所有，如需转载，需授权并注明出处

适用于板卡型号：

紫光同创PGL22G开发平台（盘古22K）

一：盘古22K开发板（紫光同创PGL22G开发平台）简介

盘古22K开发板是基于紫光同创Logos系列PGL22G芯片设计的一款FPGA开发板，全面实现国产化方案，板载资源丰富，高容量、高带宽，外围接口丰富，不仅适用于高校教学，还可以用于实验项目、项目开发，一板多用，满足多方位的开发需求。

二：实验目的

了解数码管的类型和工作原理。

三：实验要求

实现四位八段数码管同时循环显示数字0~9，数字每隔1s自加1。

四：实验原理

数码管是一种半导体发光器件，其基本单元是发光二极管。能显示4个数码管叫四位数码管。数码管按段数分为七段数码管和八段数码管，八段数码管比七段数码管多一个发光二极管单元（多一个小数点显示）；按发光二极管单元连接方式分为共阳极数码管和共阴极数码管。共阳数码管是指将所有发光二极管的阳极接到一起形成公共阳极(COM)的数码管。共阳数码管在应用时应将公共极COM接到+5V，当某一字段发光二极管的阴极为低电平时，相应字段就点亮。当某一字段的阴极为高电平时，相应字段就不亮。共阴数码管是指将所有发光二极管的阴极接到一起形成公共阴极(COM)的数码管。共阴数码管在应用时应将公共极COM接到地线GND上，当某一字段发光二极管的阳极为高电平时，相应字段就点亮。当某一字段的阳极为低电平时，相应字段就不亮。

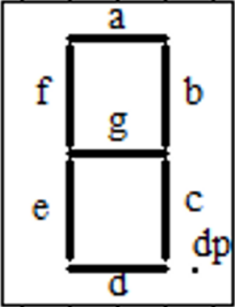
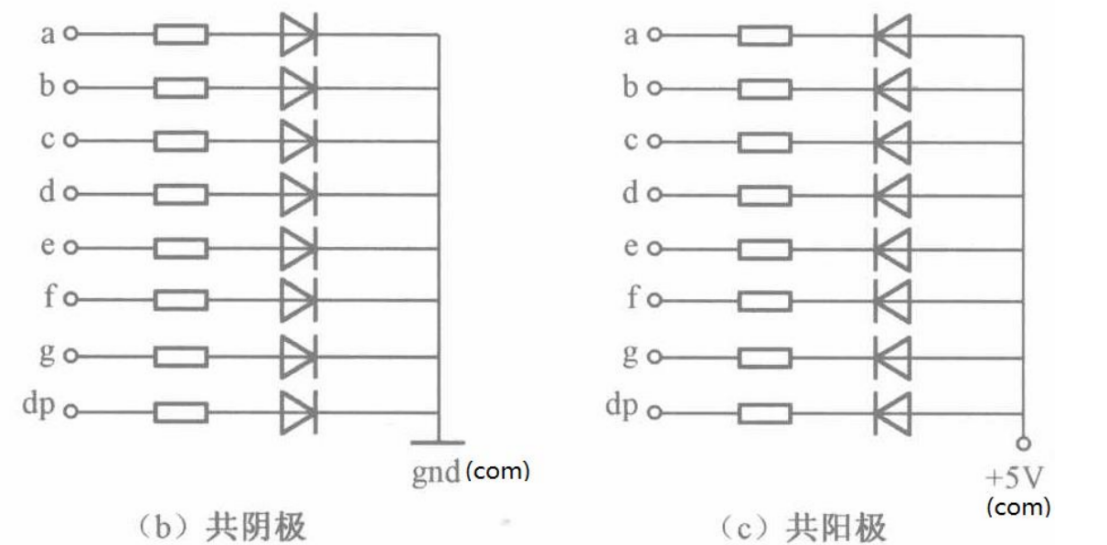
image.png

image.png

对共阴极数码管来说，其 8 个发光二极管的阴极在数码管内部全部连接在一起，所以称“共阴”，而阳极独立。对共阳极数码管来说，其 8 个发光二极管的阳极在数码管内部全部连接在一起，所以称“共阳”，而阴极独立。以共阳极数码管为例，当我们想让数码管显示数字“8”，可以给 a、b、c…g 七个引脚送低电平，数码管就显示“8”，显示数字“1”，就给 b、c 引脚低电平，其余引脚（除公共端）给高电平，数码管就显示“1”。当多位数码管应用于某一系统时，为了减少数码管占用的 I/O 口，将其段选（数码管的 a、b、c 等引脚）连接在一起，而位选（数码管的公共端）独立控制。这样我们可以通过位选信号控制哪几个数码管亮，而且在同一时刻，位选选通的所有数码管上显示的数字始终都是一样的，因为它们的段选是连接在一起的，所以送入所有数码管的段选信号都是相同的，数码管的这种显示方法叫做静态显示。对于静态显示还有一种是数码管的每一个码段都由一个单独的 I/O 端口进行驱动，其优点是编程较为简单，显示亮度较高；缺点是占用 I/O 较多，当数码管较多时，必须增加译码驱动器进行驱动，或使用串口转并口芯片来拓展端口。因而对于多位数码管的使用，一般都采用前一种方式进行电路设计，这种电路设计更为方便的是以动态方式驱动数码管。动态显示与静态显示的区别关键在于位选的控制。

五：实验源码设计

首先定义模块的输入输出。

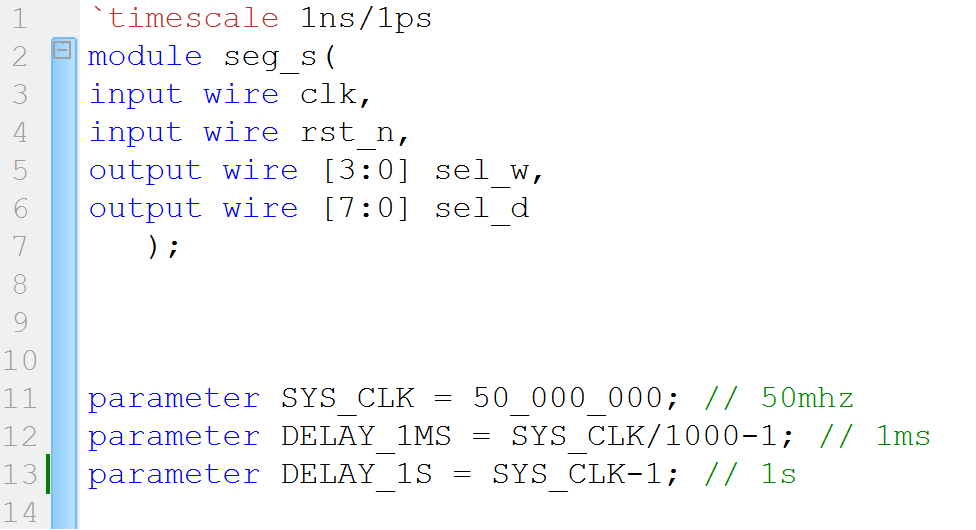
image.png

 然后通过一个计数器来控制数字的切换（即每隔1s自加1）。

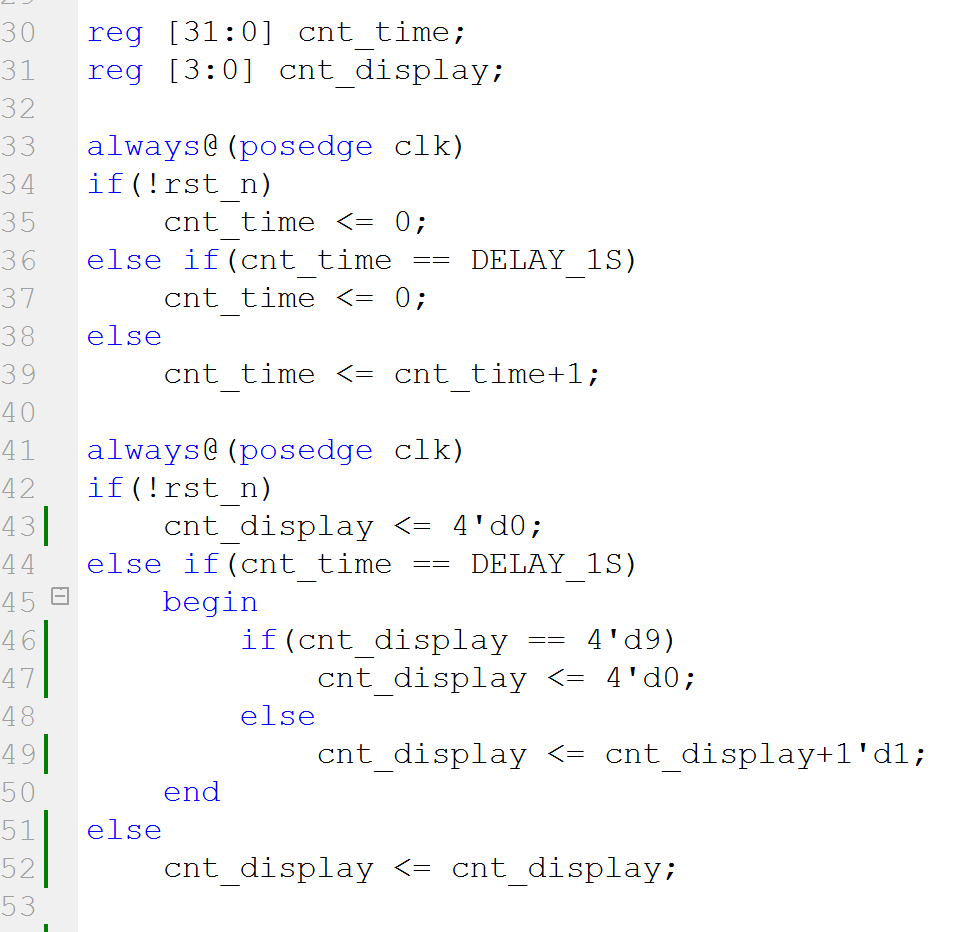
image.png

 通过一个case语句来控制数码管段选输出的数字。注意每个数字对应的段选变量display（a~g和dp）根据引脚配置的不同而变化，实际情况要根据原理图上的引脚分配来定。

image.png

 由于本次实验为静态显示，故只需要对位选全部使能，段选随着数字的自加而变化即可。

image.png

 

 *盘古PGL22G开发板

 

相关文章：

【两周学会FPGA】从0到1学习紫光同创FPGA开发|盘古PGL22G开发板学习之数码管静态显示（四）

本原创教程由深圳市小眼睛科技有限公司创作，版权归本公司所有，如需转载，需授权并注明出处 适用于板卡型号： 紫光同创PGL22G开发平台（盘古22K） 一：盘古22K开发板（紫光同创PGL22G开发…...

编程日记 2023/9/3 18:38:56

【洛谷】P3853 路标设置

原题链接：https://www.luogu.com.cn/problem/P3853 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 整体思路：二分答案 由题意知，公路上相邻路标的最大距离定义为该公路的“空旷指数”。在公路上增设一些路标&…...

编程日记 2023/9/3 18:37:55

探索图像数据中的隐藏信息：语义实体识别和关系抽取的奇妙之旅

探索图像数据中的隐藏信息：语义实体识别和关系抽取的奇妙之旅 1. 简介 1.1 背景 关键信息抽取 (Key Information Extraction, KIE)指的是是从文本或者图像中，抽取出关键的信息。针对文档图像的关键信息抽取任务作为OCR的下游任务，存在非常…...

编程日记 2023/9/3 18:36:54

Gradle问题处理

目录 一、依赖搜索问题1.1 、Gradle不在本地 Maven 存储库中进行搜索一、依赖搜索问题 1.1 、Gradle不在本地 Maven 存储库中进行搜索 场景 build.gradle文件： buildscript {repositories {mavenLocal()google()mavenCentral()}dependencies...

编程日记 2023/9/3 18:35:50

架构：C4 Model

概念 C4说穿了就是几个要素：关系——带箭头的线、元素——方块和角色、关系描述——线上的文字、元素的描述——方块和角色里的文字、元素的标记——方块和角色的颜色、虚线框（在C4里面虚线框的表达力被极大的限制了，我觉得可以给虚线框更大…...

编程日记 2023/9/3 18:34:50

数据结构学习系列之顺序表的两种修改方式

方式1&#xff1a;根据顺序表中数据元素的位置进行修改&#xff0c;代码如下&#xff1a;示例代码&#xff1a; int modify_seq_list_1(list_t *seq_list,int pos, int data){if(NULL seq_list){printf("入参为NULL\n");return -1;}if( pos < 0 || pos > seq…...

编程日记 2023/9/3 18:33:49

React：props说明

props是只读对象&#xff08;readonly&#xff09; 根据单项数据流的要求&#xff0c;子组件只能读取props中的数据&#xff0c;不能进行修改props可以传递任意数据 数字、字符串、布尔值、数组、对象、函数、JSX import FileUpdate from ./FileUpdate; export default class …...

编程日记 2023/9/3 18:32:47

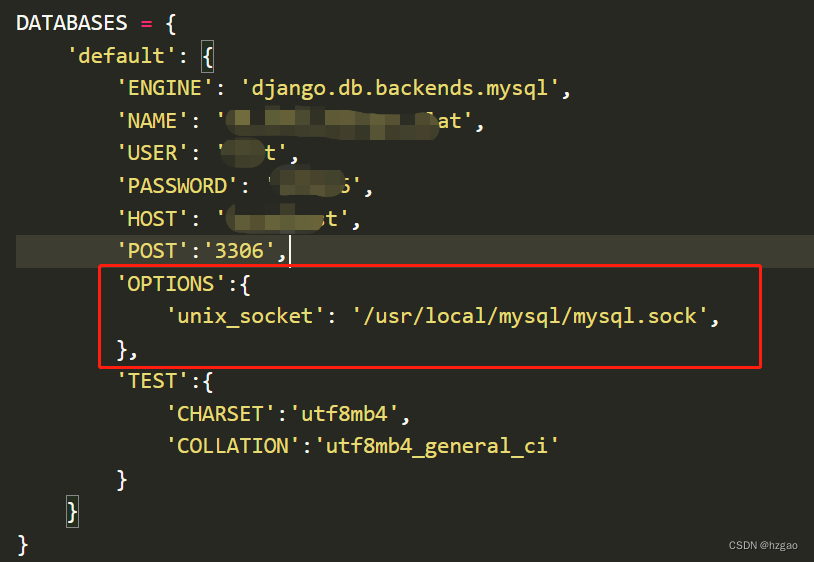
Can‘t connect to local MySQL server through socket ‘/tmp/mysql.sock‘

最近在用django框架开发后端时&#xff0c;在运行 $python manage.py makemigrations 命令时&#xff0c;报了以上错误&#xff0c;错误显示连接mysql数据库失败&#xff0c;查看了mysql数据库初始化配置文件my.cnf&#xff0c;我的mysql.sock文件存放路径配置在了/usr/local…...

编程日记 2023/9/3 18:31:46

C++的单例模式

忘记之前有没有写过单例模式了。 再记录一下&#xff1a; 我使用的代码&#xff1a; #ifndef SINGLETON_MACRO_HPP #define SINGLETON_MACRO_HPP#define SINGLETON_DECL(class_name) \ public: \static class_name& instance() { \static class_name s_instance; \return …...

编程日记 2023/9/3 18:30:45

Spring Boot 中 Nacos 配置中心使用实战

官方参考文档 https://nacos.io/zh-cn/docs/quick-start-spring-boot.html 本人实践 1、新建一个spring boot项目 我的spirngboot版本为2.5.6 2、添加一下依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-…...

编程日记 2023/9/3 18:29:45

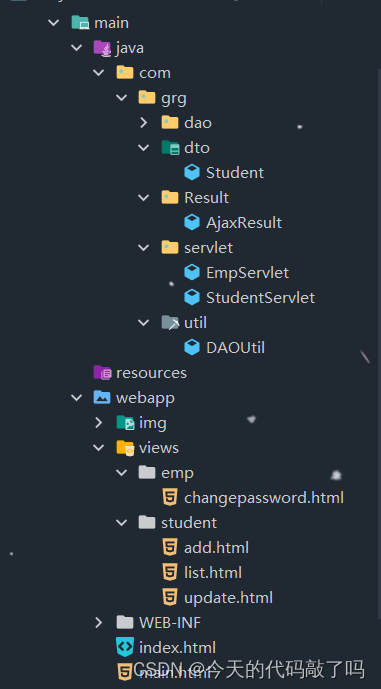
学生管理系统VueAjax版本

学生管理系统VueAjax版本 使用Vue和Ajax对原有学生管理系统进行优化 1.准备工作 创建AjaxResult类&#xff0c;对Ajax回传的信息封装在对象中 package com.grg.Result;/*** Author Grg* Date 2023/8/30 8:51* PackageName:com.grg.Result* ClassName: AjaxResult* Descript…...

编程日记 2023/9/3 18:28:44

迭代器模式简介

概念&#xff1a; 迭代器模式是一种行为型设计模式&#xff0c;它提供了一种访问集合对象元素的方法&#xff0c;而无需暴露其内部表示。通过使用迭代器&#xff0c;可以按照特定顺序遍历集合中的元素。 特点&#xff1a; 将遍历和具体集合分离&#xff0c;使得能够独立地改…...

编程日记 2023/9/3 18:27:41

四方定理c++题解

题目描述 四方定理是数论中著名的一个定理&#xff0c;指任意一个自然数都可以拆成四个自然数的平方之和。例如&#xff1a; 251^22^22^24^2 对 25来说&#xff0c;还有其他方案&#xff1a; 250^20^23^24^2 以及 250^20^20^25^2 给定一个自然数 n &#xff0c;请输出 n…...

编程日记 2023/9/3 18:26:40

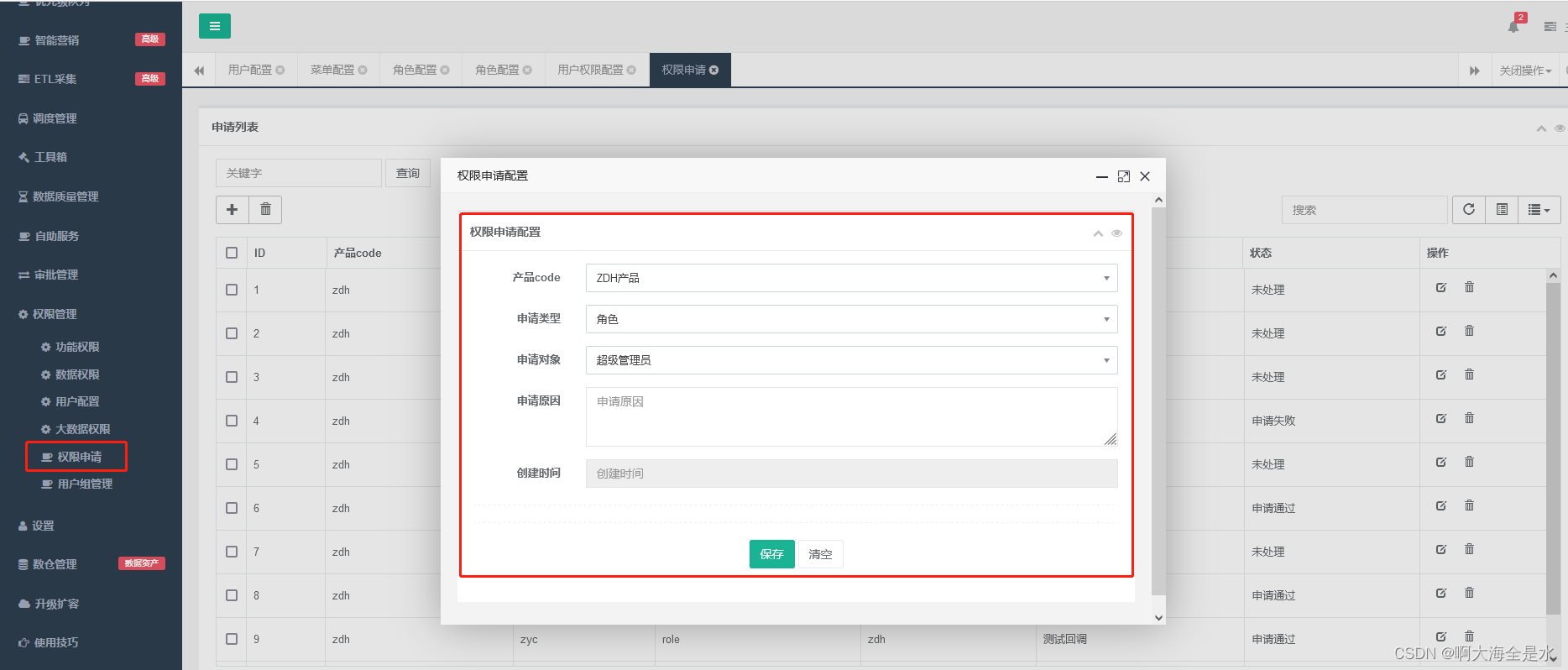
ZDH-权限模块

本次介绍基于ZDH v5.1.2版本 目录 项目源码 预览地址 安装包下载地址 ZDH权限模块 ZDH权限模块-重要名词划分 ZDH权限模块-菜单管理 ZDH权限模块-角色管理 ZDH权限模块-用户配置 ZDH权限模块-权限申请 项目源码 zdh_web: GitHub - zhaoyachao/zdh_web: 大数据采集,抽…...

编程日记 2023/9/3 18:25:39

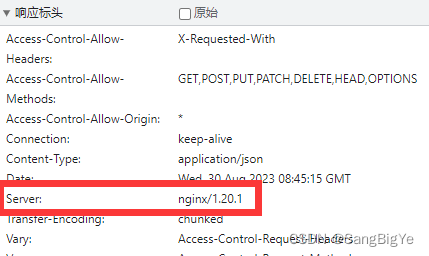
漏洞修复：在应用程序中发现不必要的 Http 响应头

描述 blablabla描述&#xff0c;一般是在返回的响应表头中出现了Server键值对&#xff0c;那我们要做的就是移除它&#xff0c;解决方案中提供了nginx的解决方案 解决方案 第一种解决方案 当前解决方案会隐藏nginx的版本号&#xff0c;但还是会返回nginx字样&#xff0c;如…...

编程日记 2023/9/3 18:24:38

什么是mkp勒索病毒，中了mkp勒索病毒怎么办？勒索病毒解密数据恢复

mkp勒索病毒是一种新兴的计算机木马病毒&#xff0c;它以加密文件的方式进行勒索&#xff0c;对用户的计算机安全造成了严重威胁。本文将介绍mkp勒索病毒的特征、影响以及应对措施&#xff0c;以便读者更好地了解和防范这种病毒。 一、mkp勒索病毒的特征 加密文件&#xff1a;…...

编程日记 2023/9/3 18:23:37

db2迁移至oracle

1.思路 &#xff08;1&#xff09;用java连接数据库&#xff08;2&#xff09;把DB2数据导出为通用的格式如csv&#xff0c;json等&#xff08;3&#xff09;导入其他数据库&#xff0c;比如oracle&#xff0c;mongodb。这个方法自由发挥的空间比较大。朋友说他会用springboot…...

编程日记 2023/9/3 18:22:37

webpack学习使用

...

编程日记 2023/9/3 18:21:36

按钮控件之2---QComboBox 复选按钮/复选框控件

1、常用函数&#xff1a; comboBox->addItem("cxq"); //添加下拉选项 combobox->clear(); //清空下拉项comboBox->setCurrentIndex(0);//设置当前的索引 int currentlndex()&#xff1a; //返回当前项的序号&#xff0c;第一个项的序号…...

编程日记 2023/9/3 18:20:35

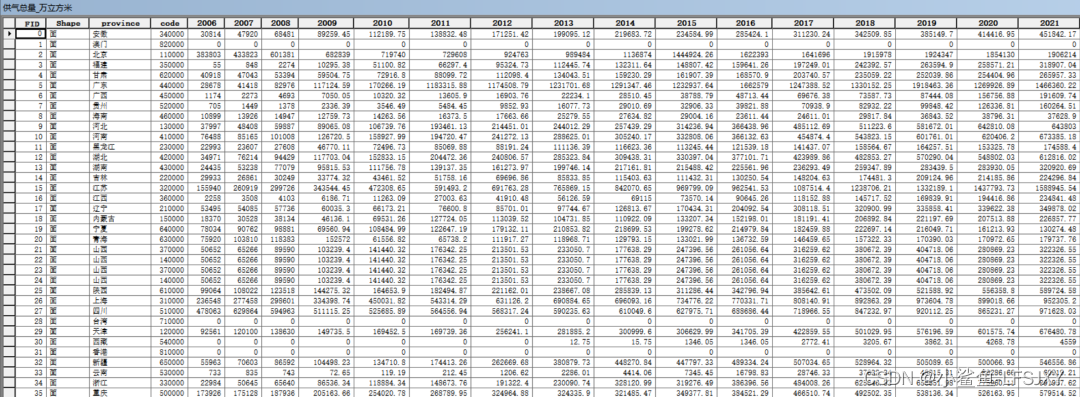
【数据分享】2006-2021年我国省份级别的燃气相关指标（免费获取\20多项指标）

《中国城市建设统计年鉴》中细致地统计了我国城市市政公用设施建设与发展情况&#xff0c;在之前的文章中&#xff0c;我们分享过基于2006-2021年《中国城市建设统计年鉴》整理的2006—2021年我国省份级别的市政设施水平相关指标、2006-2021年我国省份级别的各类建设用地面积数…...

编程日记 2023/9/3 18:19:34

React hook之useRef

React useRef 详解 useRef 是 React 提供的一个 Hook&#xff0c;用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途&#xff0c;下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

编程新知 2025/6/11 15:21:26

多场景 OkHttpClient 管理器 - Android 网络通信解决方案

下面是一个完整的 Android 实现&#xff0c;展示如何创建和管理多个 OkHttpClient 实例&#xff0c;分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

编程新知 2025/12/15 1:34:37

Matlab | matlab常用命令总结

常用命令 一、 基础操作与环境二、 矩阵与数组操作（核心）三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结，涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

编程新知 2025/8/11 1:05:59

智能分布式爬虫的数据处理流水线优化：基于深度强化学习的数据质量控制

在数字化浪潮席卷全球的今天&#xff0c;数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具&#xff0c;在大规模数据获取中发挥着关键作用。然而&#xff0c;传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时&#xff0c;常出现数据质…...

编程新知 2026/2/6 1:04:23

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台

🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型（LLM）的广泛应用，开发者常面临多个挑战： 各大模型（OpenAI、Claude、Gemini、Ollama）接口风格不统一；缺乏一个统一平台进行模型调用与测试；本地模型 Ollama 的集成与前…...

编程新知 2026/1/25 3:31:07

laravel8+vue3.0+element-plus搭建方法

创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

编程新知 2025/10/15 0:25:46

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/9/20 12:14:18

【Linux】Linux 系统默认的目录及作用说明

博主介绍&#xff1a;✌全网粉丝23W&#xff0c;CSDN博客专家、Java领域优质创作者&#xff0c;掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围&#xff1a;SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

编程新知 2026/1/29 2:30:31

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)

前言&#xff1a; 双亲委派机制对于面试这块来说非常重要&#xff0c;在实际开发中也是经常遇见需要打破双亲委派的需求&#xff0c;今天我们一起来探索一下什么是双亲委派机制&#xff0c;在此之前我们先介绍一下类的加载器。 目录 ​编辑 前言&#xff1a; 类加载器 1. …...

编程新知 2026/1/23 7:37:12

SQL Server 触发器调用存储过程实现发送 HTTP 请求

文章目录 需求分析解决第 1 步：前置条件，启用 OLE 自动化方式 1：使用 SQL 实现启用 OLE 自动化方式 2：Sql Server 2005启动OLE自动化方式 3：Sql Server 2008启动OLE自动化第 2 步：创建存储过程第 3 步：创建触发器扩展 - 如何调试？第 1 步：登录 SQL Server 2008第 2 步…...

编程新知 2025/9/11 6:56:11