数据结构--6.0最短路径
目录
一、迪杰斯特拉算法(Dijkstra)
二、弗洛伊德算法(Floyd)
在网图和非网图中,最短路径的含义是不同的。
——网图是两顶点经过的边上的权值之和最少的路径。
——非网图是两顶点之间经过的边数最少的路径。
我们把路径起始的第一个顶点称为源头,最后一个顶点称为终点。
关于最短路径的算法:
1、迪杰斯特拉算法(Dijkstra)
2、弗洛伊德算法(Floyd)
一、迪杰斯特拉算法(Dijkstra)
#include <stdio.h>
#include <stdlib.h>#define MAXVEX 9
#define INFINITY 65536typedef int Patharc[MAXVEX]; //用于存储最短路径下标的数组
typedef int ShortPathTable[MAXVEX]; //用于存储到各点最短路径的权值 void ShortestPath_Dijkstra(MGraph G , int V0,Patharc *p,ShortPathTable *D)
{int v,w,k,min;int final[MAXVEX]; //final[w]=1 表示已经求得顶点v0到vw的最短路径 //初始化数据 for(v=0;v<G.numVertexes; v++){final[v] = 0; //全部顶点初始化为未找到最短路径 (*D)[v] = G.arc{V0}[v]; //将与v0点有连接线的顶点加上权值 (*p)[v] = 0; //初始化路径数组p为0 }(*D)[V0] = 0; //v0至v0的路径为0 final[v0] = 1; //v0至v0不需要求路径 //开始主循环,每次求得v0到某个v顶点的最短路径 for(v=1;v<G.numVertexes;v++){min = INFINITY;for(w =0; w<G.numVertexes; v++){if(!final[w]&&(*D)[w]<min){k = w;min = (*D)[w]; } } final[k] = 1;//将目前找到的最短路径置1 //修正当前最短路径及距离 for(w=0; w<G.numVextexes;w++){//如果经过v顶点的路径比现在这条路径的长度短的话,更新! if( !final[w]&&(min+G.arc[k][w] < (*D)[w])){(*D)[w] = min + G.arc[k][w]; //修改当前路径长度 (*p)[w] = k; //存放前驱顶点 }} }
}二、弗洛伊德算法(Floyd)
弗洛伊德算法非常简洁优雅。
#include <stdio.h>
#include <stdlib.h>#define MAXVEX 9
#define INFINITY 65536typedef int Pathmatirx[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];void ShortestPath_Floyd(MGraph.G,Pathmatirx *p,ShortPathTable *D)
{int v,w,k;//初始化 D 和 p for(v=0;v<G.numVertexes;w++){for(w=0;w<G.numVertexes;w++){(*D)[v][w] = G.matirx[v][m];(*p)[v][w] = w;}}//弗洛伊德算法 for(k=0;k<G.numVertexes;k++){for(v=0;v<G.numVertexes;v++){for(w=0;w<G.numVertexes;w++){if((*D)[v][w] > ((*D)[v][k] + (*D)[k][w])){(*D)[v][w] = (*D)[v][k] + (*D)[k][w];(*p)[v][w] = (*p)[v][k];}}}}
} 相关文章:

数据结构--6.0最短路径
目录 一、迪杰斯特拉算法(Dijkstra) 二、弗洛伊德算法(Floyd) 在网图和非网图中,最短路径的含义是不同的。 ——网图是两顶点经过的边上的权值之和最少的路径。 …...

Docker进阶:mysql 主从复制、redis集群3主3从【扩缩容案例】
Docker进阶:mysql 主从复制、redis集群3主3从【扩缩容案例】 一、Docker常规软件安装1.1 docker 安装 tomcat(默认最新版)1.2 docker 指定安装 tomcat8.01.3 docker 安装 mysql 5.7(数据卷配置)1.4 演示--删除mysql容器…...

遗传算法决策变量降维的matlab实现
1.案例背景 1.1遗传算法概述 遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。它最初由美国Michigan大学的J. Holland教授提出,1967年, Holland 教授的学生 Bagley在其博士论文中首次提出了“遗传…...

基于Open3D和PyTorch3D读取三维数据格式OBJ
本节将讨论另一种广泛使用的3D数据文件格式,即OBJ文件格式。OBJ文件格式最初由Wavefront Technologies Inc.开发。与PLY文件格式类似,OBJ格式也有ASCII版本和二进制版本。二进制版本是专有的且未记录文档。本章主要讨论ASCII版本。 与之前类似,将通过示例来学习文件格式。第…...

带纽扣电池产品出口澳洲安全标准,纽扣电池IEC 60086认证
澳大利亚政府公布了《消费品(纽扣/硬币电池)安全标准》和《消费品(纽扣/硬币电池)信息标准》。届时出口纽扣/硬币电池以及含有纽扣/硬币电池产品到澳大利亚的供应商,必须遵守这些标准中的要求。 一、 安全标准及信息标…...
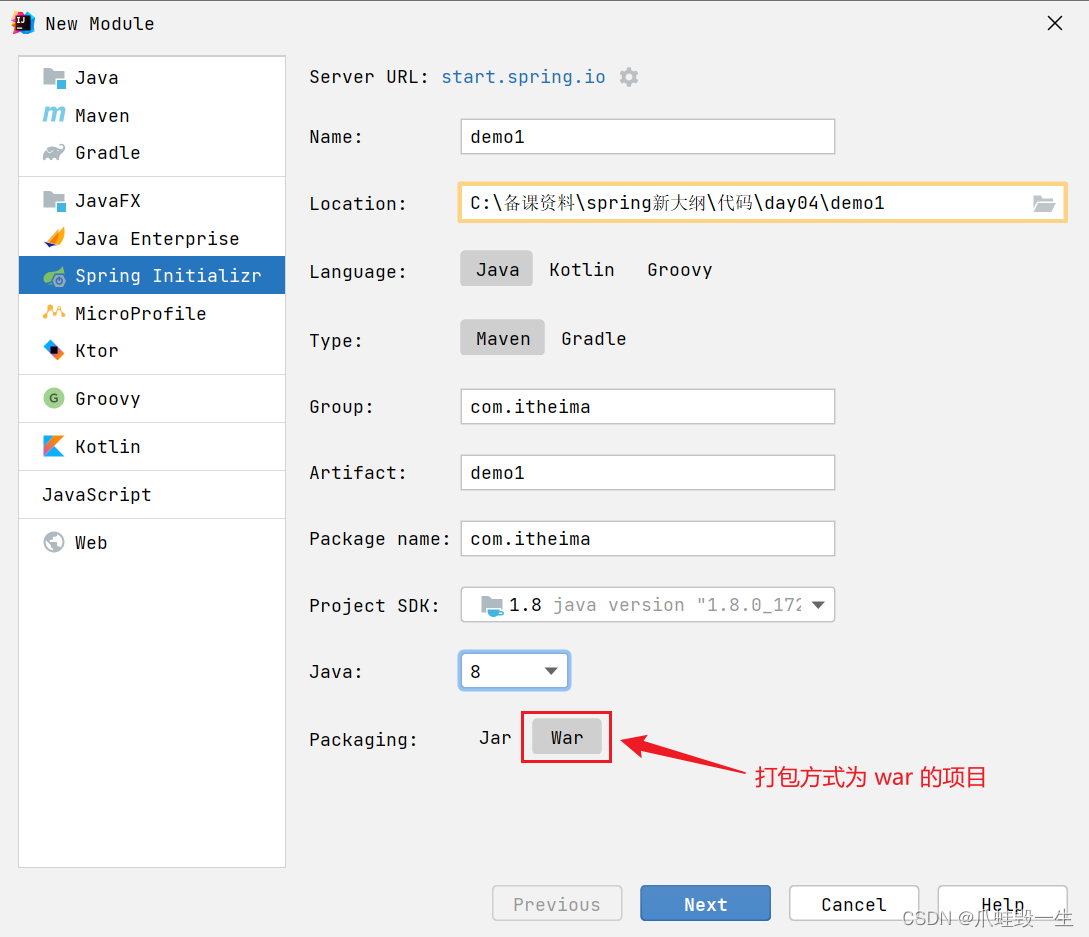
spring高级源码50讲-37-42(springBoot)
Boot 37) Boot 骨架项目 如果是 linux 环境,用以下命令即可获取 spring boot 的骨架 pom.xml curl -G https://start.spring.io/pom.xml -d dependenciesweb,mysql,mybatis -o pom.xml也可以使用 Postman 等工具实现 若想获取更多用法,请参考 curl …...
腾讯云、阿里云、华为云便宜云服务器活动整理汇总
云服务器的选择是一个很重要的事情,避免产生不必要的麻烦,建议选择互联网大厂提供的云计算服务,腾讯云、阿里云、华为云就是一个很不错的选择,云服务器稳定性、安全性以及售后各方面都更受用户认可,下面小编给大家整理…...
 测试点全过)
L1-055 谁是赢家(Python实现) 测试点全过
前言: {\color{Blue}前言:} 前言: 本系列题使用的是,“PTA中的团体程序设计天梯赛——练习集”的题库,难度有L1、L2、L3三个等级,分别对应团体程序设计天梯赛的三个难度。更新取决于题目的难度,…...
开发一个npm包
1 注册一个npm账号 npm https://www.npmjs.com/ 2 初始化一个npm 项目 npm init -y3编写一段代码 function fn(){return 12 }exports.hellofn;4发布到全局node_module npm install . -g5测试代码 创建一个text文件 npm link heath_apisnode index.js6登录(我默认的 https…...
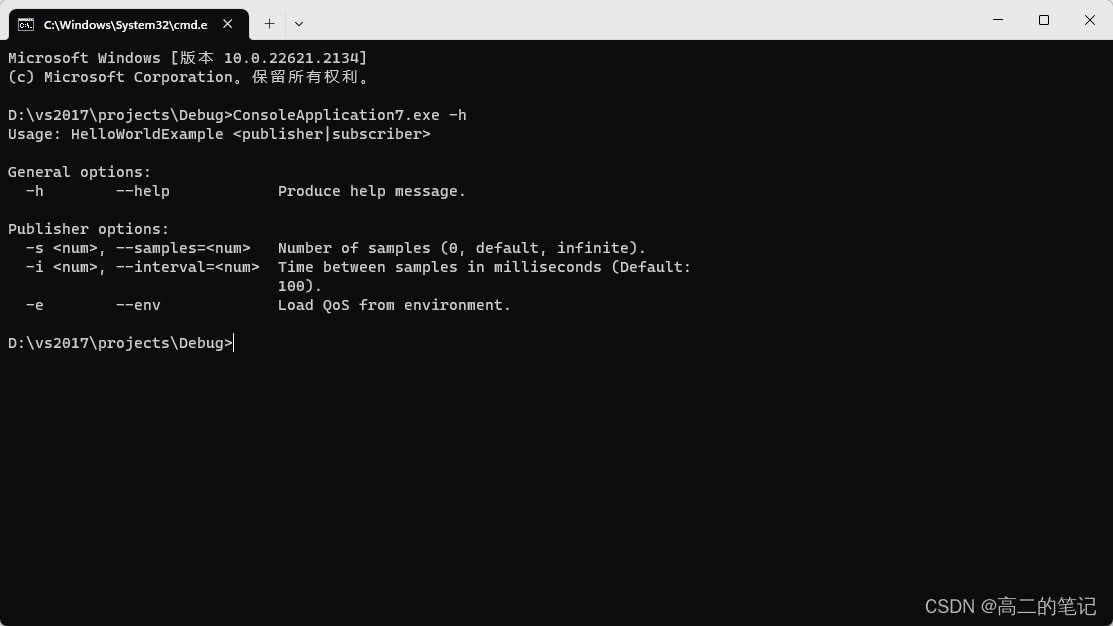
介绍几种使用工具
FileWatch,观测文件变化,源码地址:https://github.com/ThomasMonkman/filewatch nlohmann::json,json封装解析,源码地址:https://github.com/nlohmann/json optionparser,解析选项,源…...

Vue:关于声明式导航中的 跳转、高亮、以及两个类名的定制
声明式导航-导航链接 文章目录 声明式导航-导航链接router-link的两大特点(能跳转、能高亮)声明式导航-两个类名定制两个高亮类名 实现导航高亮,实现方式其实,css,JavaScript , Vue ,都可以实现。其实关于路由导航&…...

Sharding-JDBC分库分表-自动配置与分片规则加载原理-3
Sharding JDBC自动配置的原理 与所有starter一样,shardingsphere-jdbc-core-spring-boot-starter也是通过SPI自动配置的原理实现分库分表配置加载,spring.factories文件中的自动配置类shardingsphere-jdbc-core-spring-boot-starter功不可没,…...

E8267D 是德科技矢量信号发生器
描述 最先进的微波信号发生器 安捷伦E8267D PSG矢量信号发生器是业界首款集成式微波矢量信号发生器,I/Q调制最高可达44 GHz,典型输出功率为23 dBm,最高可达20 GHz,对于10 GHz信号,10 kHz偏移时的相位噪声为-120 dBc/…...

Git git fetch 和 git pull 区别
git pull和git fetch的作用都是用于从远程仓库获取最新代码,但它们之间有一些区别。 git pull会自动执行两个操作:git fetch和git merge。它从远程仓库获取最新代码,并将其合并到当前分支中。 示例:运行git pull origin master会从…...

软件UI工程师工作的岗位职责(合集)
软件UI工程师工作的岗位职责1 职责: 1.负责产品的UI视觉设计(手机软件界面 网站界面 图标设计产品广告及 企业文化的创意设计等); 2.负责公司各种客户端软件客户端的UE/UI界面及相关图标制作; 3.设定产品界面的整体视觉风格; 4.参与产品规划构思和创意过程&…...
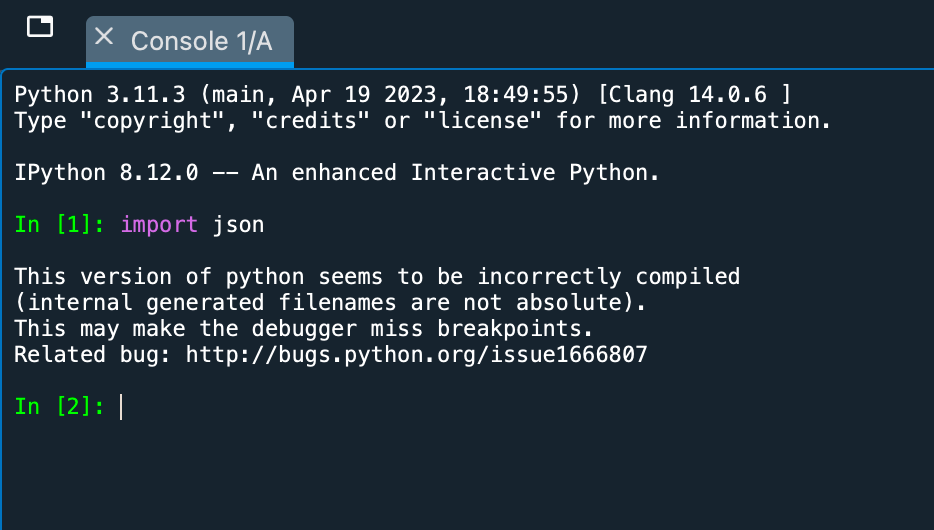
Mac系统Anaconda环境配置Python的json库
本文介绍在Mac电脑的Anaconda环境中,配置Python语言中,用以编码、解码、处理JSON数据的json库的方法;在Windows电脑中配置json库的方法也是类似的,大家可以一并参考。 JSON(JavaScript Object Notation)是一…...

Python数据分析与数据挖掘:解析数据的力量
引言: 随着大数据时代的到来,数据分析和数据挖掘已经成为许多行业中不可或缺的一部分。在这个信息爆炸的时代,如何从大量的数据中提取有价值的信息,成为了企业和个人追求的目标。而Python作为一种强大的编程语言,提供…...
)
我的私人笔记(安装hive)
1.hive下载:Index of /dist/hive/hive-1.2.1 或者上传安装包至/opt/software:rz或winscp上传 2.解压 cd /opt/software tar -xzvf apache-hive-1.2.1-bin.tar.gz -C /opt/servers/ 3.重命名 mv apache-hive-1.2.1-bin hive 4.配置环境变量 vi /etc/…...
【kubernetes】k8s部署APISIX及在KubeSphere使用APISIX
Apache APISIX https://apisix.apache.org/ 功能比nginx-ingress更强 本文采用2.5.0版本 https://apisix.apache.org/zh/docs/apisix/2.15/getting-started/ 概述内容来源于官方,学习于马士兵云原生课程 概述 Apache APISIX 是什么? Apache APISIX 是 …...
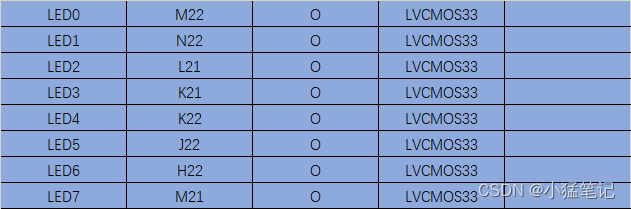
串口接收数据-控制LED灯
目标 通过串口接收数据,对数据分析,控制8个LED灯按照设定时间闪烁。 8个LED灯可以任意设计,是否闪烁。闪烁时间按ms计算,通过串口发送,可设置1~4,294,967,296ms,也就是4字节数据协议自拟,有数…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
