2023高教社杯数学建模思路 - 案例:ID3-决策树分类算法
文章目录
- 0 赛题思路
- 1 算法介绍
- 2 FP树表示法
- 3 构建FP树
- 4 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 算法介绍
FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,他与Apriori算法一样也是用来挖掘频繁项集的,不过不同的是,FP-Tree算法是Apriori算法的优化处理,他解决了Apriori算法在过程中会产生大量的候选集的问题,而FP-Tree算法则是发现频繁模式而不产生候选集。但是频繁模式挖掘出来后,产生关联规则的步骤还是和Apriori是一样的。
常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FP-growth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。
FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。
2 FP树表示法
FP树通过逐个读入事务,并把事务映射到FP树中的一条路径来构造。由于不同的事务可能会有若干个相同的项,因此它们的路径可能部分重叠。路径相互重叠越多,使用FP树结构获得的压缩效果越好;如果FP树足够小,能够存放在内存中,就可以直接从这个内存中的结构提取频繁项集,而不必重复地扫描存放在硬盘上的数据。
一颗FP树如下图所示:
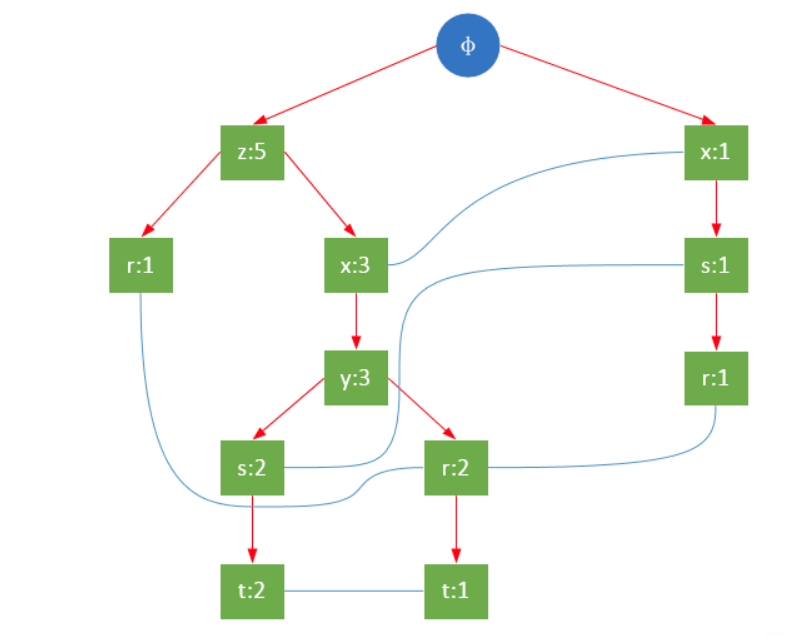
通常,FP树的大小比未压缩的数据小,因为数据的事务常常共享一些共同项,在最好的情况下,所有的事务都具有相同的项集,FP树只包含一条节点路径;当每个事务都具有唯一项集时,导致最坏情况发生,由于事务不包含任何共同项,FP树的大小实际上与原数据的大小一样。
FP树的根节点用φ表示,其余节点包括一个数据项和该数据项在本路径上的支持度;每条路径都是一条训练数据中满足最小支持度的数据项集;FP树还将所有相同项连接成链表,上图中用蓝色连线表示。
为了快速访问树中的相同项,还需要维护一个连接具有相同项的节点的指针列表(headTable),每个列表元素包括:数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针。
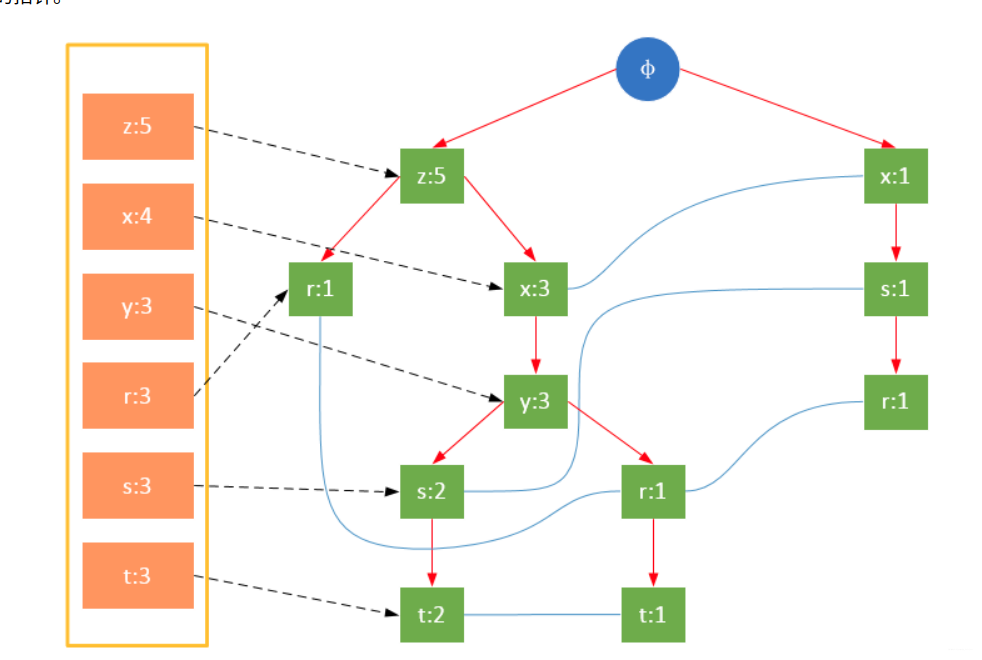
3 构建FP树
现在有如下数据:
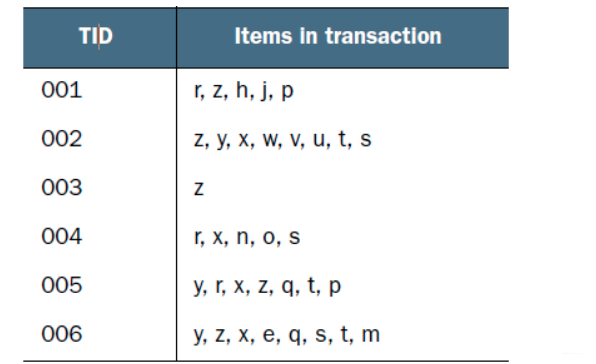
FP-growth算法需要对原始训练集扫描两遍以构建FP树。
第一次扫描,过滤掉所有不满足最小支持度的项;对于满足最小支持度的项,按照全局最小支持度排序,在此基础上,为了处理方便,也可以按照项的关键字再次排序。
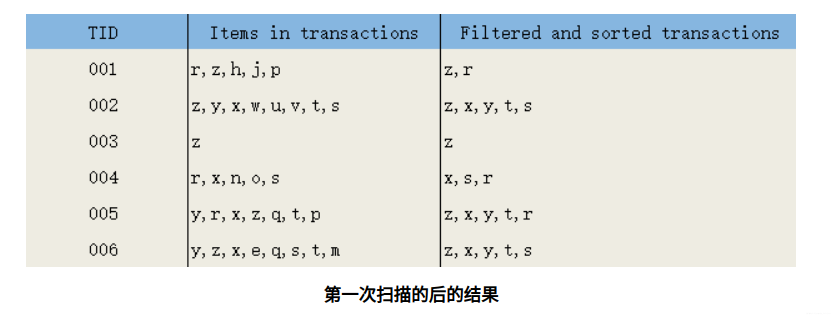
第二次扫描,构造FP树。
参与扫描的是过滤后的数据,如果某个数据项是第一次遇到,则创建该节点,并在headTable中添加一个指向该节点的指针;否则按路径找到该项对应的节点,修改节点信息。具体过程如下所示:
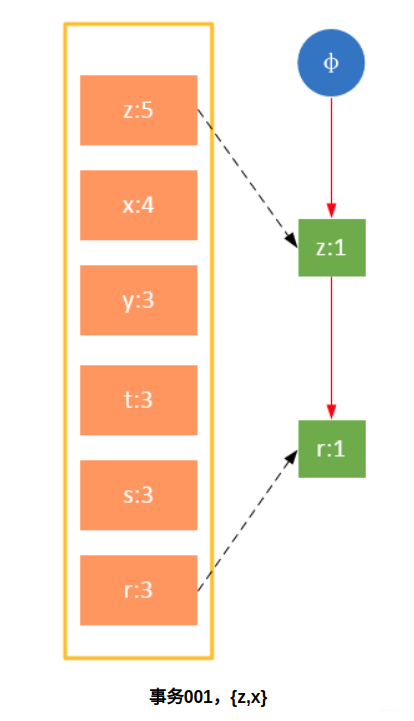
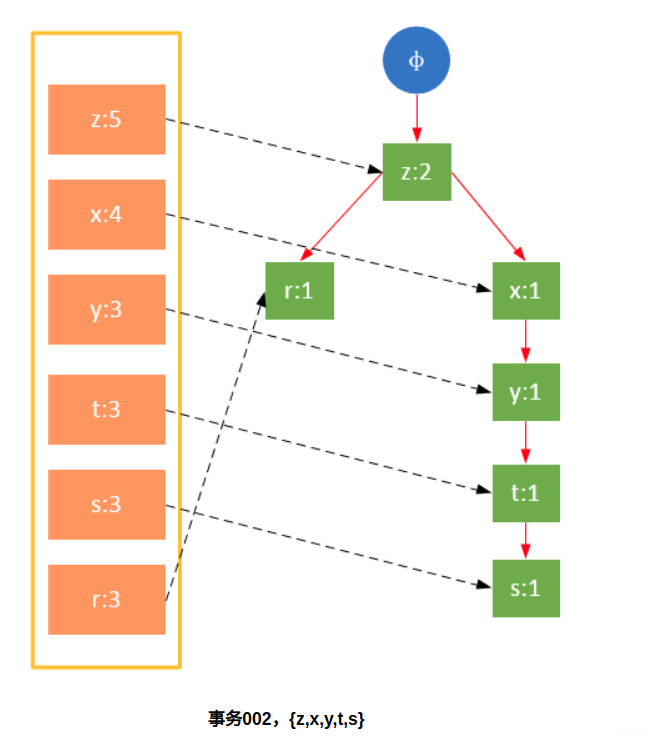
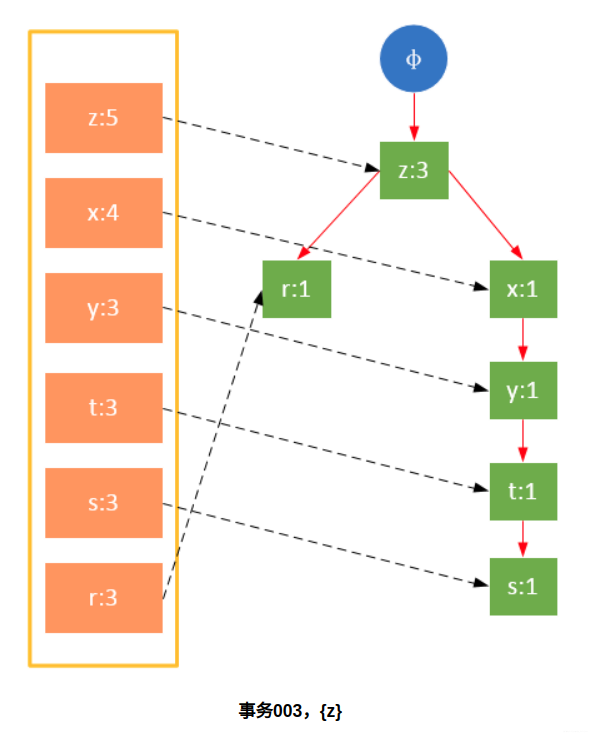
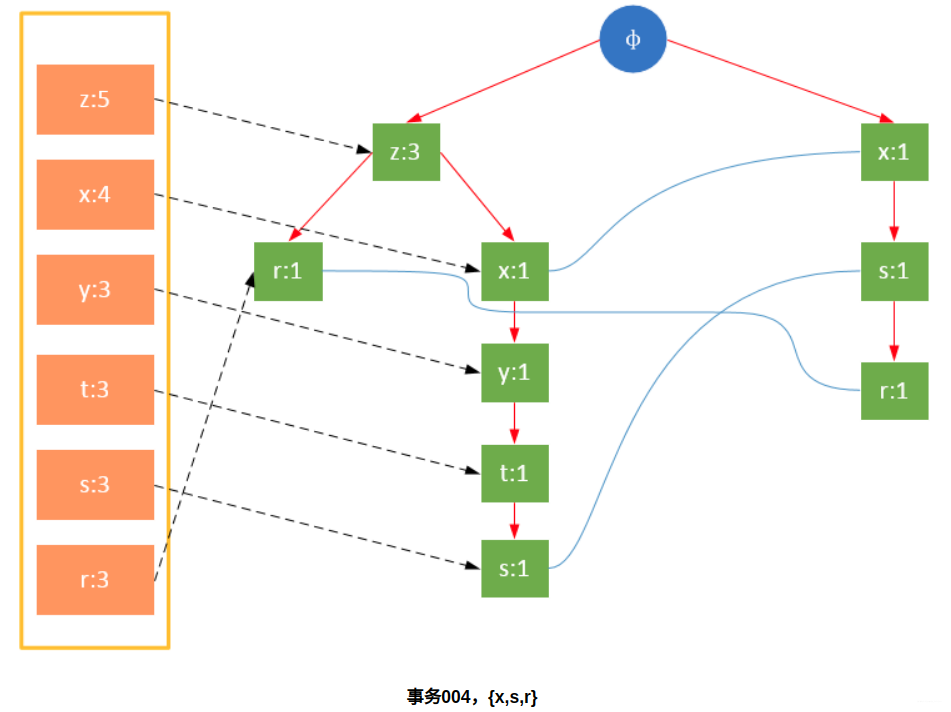
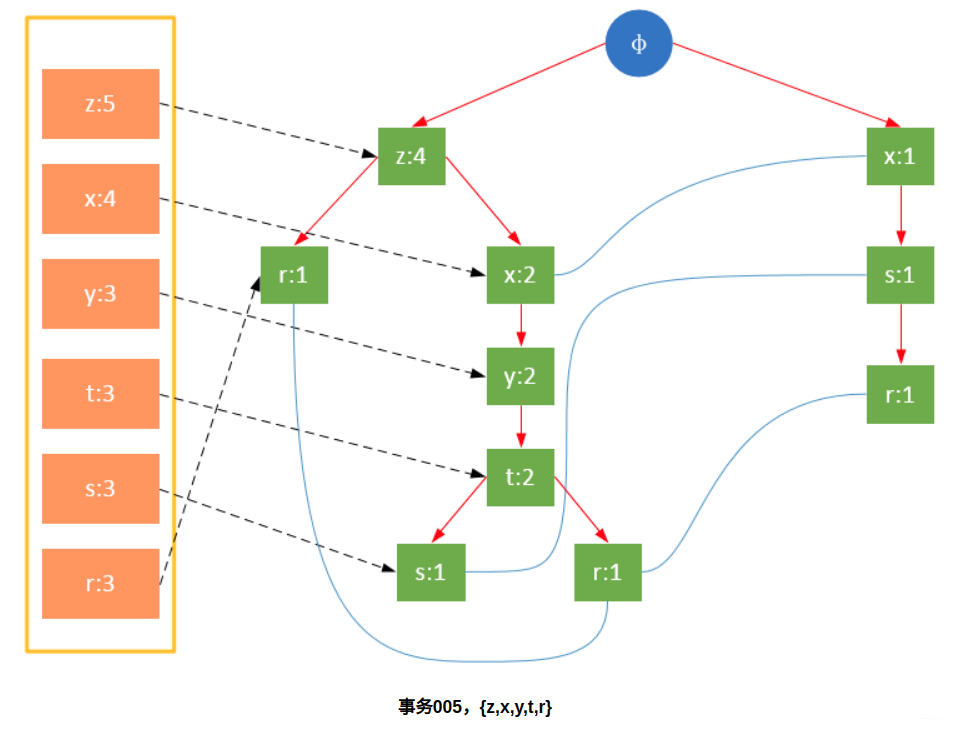
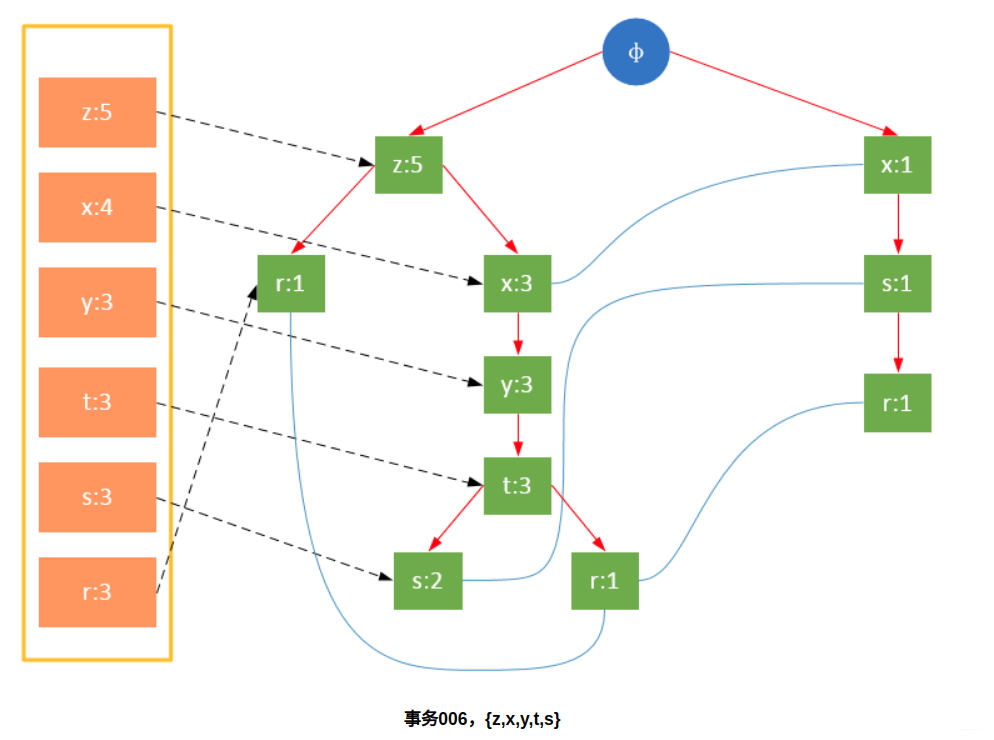
从上面可以看出,headTable并不是随着FPTree一起创建,而是在第一次扫描时就已经创建完毕,在创建FPTree时只需要将指针指向相应节点即可。从事务004开始,需要创建节点间的连接,使不同路径上的相同项连接成链表。
4 实现代码
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDatdef createInitSet(dataSet):retDict = {}for trans in dataSet:fset = frozenset(trans)retDict.setdefault(fset, 0)retDict[fset] += 1return retDictclass treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccurself.nodeLink = Noneself.parent = parentNodeself.children = {}def inc(self, numOccur):self.count += numOccurdef disp(self, ind=1):print(' ' * ind, self.name, ' ', self.count)for child in self.children.values():child.disp(ind + 1)def createTree(dataSet, minSup=1):headerTable = {}#此一次遍历数据集, 记录每个数据项的支持度for trans in dataSet:for item in trans:headerTable[item] = headerTable.get(item, 0) + 1#根据最小支持度过滤lessThanMinsup = list(filter(lambda k:headerTable[k] < minSup, headerTable.keys()))for k in lessThanMinsup: del(headerTable[k])freqItemSet = set(headerTable.keys())#如果所有数据都不满足最小支持度,返回None, Noneif len(freqItemSet) == 0:return None, Nonefor k in headerTable:headerTable[k] = [headerTable[k], None]retTree = treeNode('φ', 1, None)#第二次遍历数据集,构建fp-treefor tranSet, count in dataSet.items():#根据最小支持度处理一条训练样本,key:样本中的一个样例,value:该样例的的全局支持度localD = {}for item in tranSet:if item in freqItemSet:localD[item] = headerTable[item][0]if len(localD) > 0:#根据全局频繁项对每个事务中的数据进行排序,等价于 order by p[1] desc, p[0] descorderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: (p[1],p[0]), reverse=True)]updateTree(orderedItems, retTree, headerTable, count)return retTree, headerTabledef updateTree(items, inTree, headerTable, count):if items[0] in inTree.children: # check if orderedItems[0] in retTree.childreninTree.children[items[0]].inc(count) # incrament countelse: # add items[0] to inTree.childreninTree.children[items[0]] = treeNode(items[0], count, inTree)if headerTable[items[0]][1] == None: # update header tableheaderTable[items[0]][1] = inTree.children[items[0]]else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]])if len(items) > 1: # call updateTree() with remaining ordered itemsupdateTree(items[1:], inTree.children[items[0]], headerTable, count)def updateHeader(nodeToTest, targetNode): # this version does not use recursionwhile (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list!nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNodesimpDat = loadSimpDat()
dictDat = createInitSet(simpDat)
myFPTree,myheader = createTree(dictDat, 3)
myFPTree.disp()
上面的代码在第一次扫描后并没有将每条训练数据过滤后的项排序,而是将排序放在了第二次扫描时,这可以简化代码的复杂度。
控制台信息:

建模资料
资料分享: 最强建模资料


相关文章:

2023高教社杯数学建模思路 - 案例:ID3-决策树分类算法
文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模…...

springboot docker
在Spring Boot中使用Docker可以帮助你将应用程序与其依赖的容器化,并简化部署和管理过程。 当你在Spring Boot中使用Docker时,你的代码不需要特殊的更改。你可以按照通常的方式编写Spring Boot应用程序。 java示例代码,展示了如何编写一个基…...
docker-compose 部署nacos 整合 postgresql 为DB
标题docker-compose 部署nacos 整合 postgresql 为DB 前提: 已经安装好postgresql数据库 先创建好一个数据库 nacos,执行以下sql: /** Copyright 1999-2018 Alibaba Group Holding Ltd.** Licensed under the Apache License, Version 2.0 (the "…...
详解 ElasticSearch Kibana 配置部署
默认安装部署所在机器允许外网 SSH工具 Putty 链接:https://pan.baidu.com/s/1b6gumtsjL_L64rEsOdhd4A 提取码:lxs9 Winscp 链接:https://pan.baidu.com/s/1tD8_2knvv0EJ5OYvXP6VTg 提取码:lxs9 WinSCP安装直接下一步到完成…...
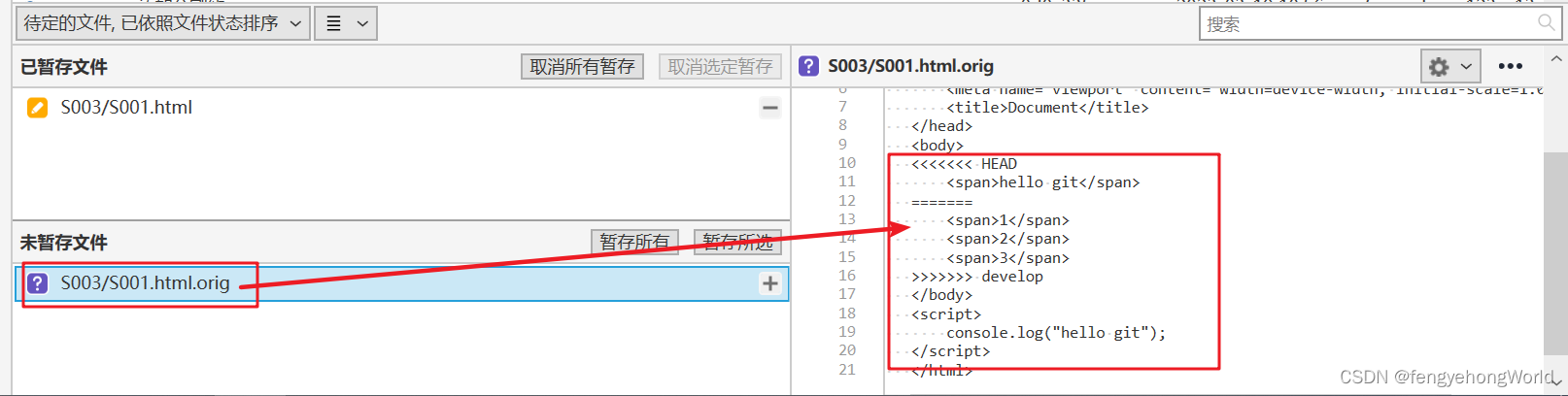
SourceTree 使用技巧
参考资料 SourceTree使用教程(一)—克隆、提交、推送SourceTree的软合并、混合合并、强合并区别SourceTree 合并分支上的多个提交,一次性合并分支的多次提交至另一分支,主分支前进时的合并冲突解决 目录 一. 基础设置1.1 用户信息…...

VIRTIO-BLK代码分析(0)概述
也无风雨也无晴。- 苏轼(宋) 接下来介绍VIRTIO相关内容。首先从VIRTIO-BLK开始分析,VIRTIO-BLK各部分交互图如下所示: 这里包含以下几个部分: Guest UserSpace:虚拟机用户空间,如虚拟机中运行f…...
)
【2023年11月第四版教材】第10章《进度管理》(第一部分)
第10章《进度管理》(第一部分) 1 章节说明2 管理基础3 管理过程3.1 管理的过程★★★3.2 管理ITTO汇总★★★ 1 章节说明 【本章分值预测】大部分内容不变,细节有一些变化,预计选择题考3-4分,案例和论文 都有可能考&a…...

【多线程案例】生产者消费者模型(堵塞队列)
文章目录 1. 什么是堵塞队列?2. 堵塞队列的方法3. 生产者消费者模型4. 自己实现堵塞队列 1. 什么是堵塞队列? 堵塞队列也是队列,故遵循先进先出的原则。但堵塞队列是一种线程安全的数据结构,可以避免线程安全问题,当队…...
数据结构与算法基础-学习-30-插入排序之直接插入排序、二分插入排序、希尔排序
一、排序概念 将一组杂乱无章的数据按一定规律顺次排列起来。 将无序序列排成一个有序序列(由小到大或由大到小)的运算。 二、排序方法分类 1、按数据存储介质 名称描述内部排序数据量不大、数据在内存,无需内外交换存交换存储。外部排序…...

Qt+C++桌面计算器源码
程序示例精选 QtC桌面计算器源码 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对<<QtC桌面计算器源码>>编写代码,代码整洁,规则,易读。 学习与…...
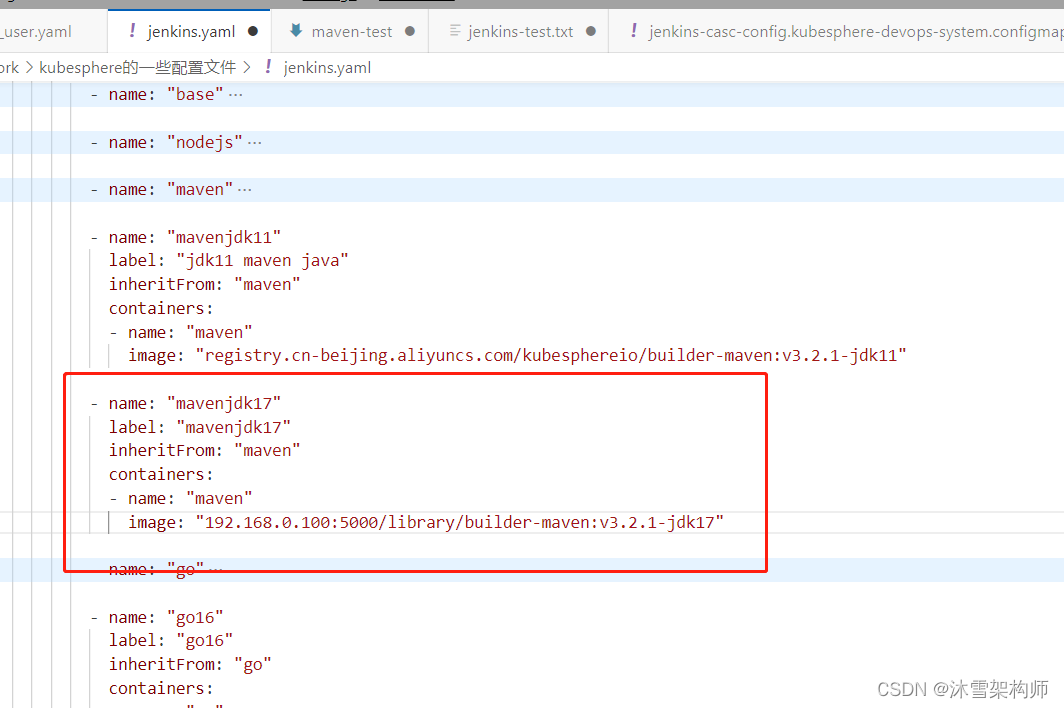
kubesphere安装Maven+JDK17 流水线打包
kubesphere 3.4.0版本,默认支持的jav版本是8和11,不支持17 。需要我们自己定义JenKins Agent 。方法如下: 一、构建镜像 1、我们需要从Jenkins Agent的github仓库拉取master最新源码,最新源码里已经支持jdk17了。 git clone ht…...

百度搜索清理大量低质量网站
我是卢松松,点点上面的头像,欢迎关注我哦! 据部分站长爆料:百度大规模删低质量网站的百度资源站长平台权限,很多网站都被删除了百度站长资源平台后台权限,以前在百度后台添加的网站大量被删除!…...

WPF数据模板
样式提供了基本的格式化能力,但它们不能消除到目前为止看到的列表的最重要的局限性:不管如何修改ListBoxItem,它都只是ListBoxItem,而不是功能更强大的元素组合。并且因为每个ListBoxItem只支持单个绑定字段,所以不可能…...

浙江绿农环境:将废弃矿山变耕地,为生态文明贡献力量
近年来,随着可持续发展理念在中国乃至全球的日益普及,浙江绿农生态环境有限公司以其独特的创新和实践,成为了绿色发展的典范,在奋进新时代、建设新天堂的背景下,绿农环境在杭州市固废治理行业迈出坚实的步伐࿰…...

HTML/CSS盒子模型
盒子:页面中的所有的元素(标签),都可以看做一个盒子,由盒子将页面中的元素包含在一个矩形区域内,通过盒子的视角更加方便的进行页面布局 盒子模型的组成: 内容区域(contentÿ…...

《Java面向对象程序设计》学习笔记——CSV文件的读写与处理
笔记汇总:《Java面向对象程序设计》学习笔记 笔记记录的不是非常详实,如果有补充的建议或纠错,请踊跃评论留言!!! 什么是CSV文件 CSV文件的定义 CSV 是英文 comma-separated values 的缩写࿰…...

opencv 案例05-基于二值图像分析(简单缺陷检测)
缺陷检测,分为两个部分,一个部分是提取指定的轮廓,第二个部分通过对比实现划痕检测与缺角检测。本次主要搞定第一部分,学会观察图像与提取图像ROI对象轮廓外接矩形与轮廓。 下面是基于二值图像分析的大致流程 读取图像将图像转换…...

Elasticsearch入门介绍
应用场景 1 它提供了强大的搜索功能,可以实现类似百度、谷歌等搜索。 2 可以搜索日志或者交易数据,用来分析商业趋势、搜集日志、分析系统瓶颈或者运行发展等等 3 可以提供预警功能(持续的查询分析某个数据,如果超过一定的值&a…...
QML Book 学习基础3(动画)
目录 主要动画元素 例子: 非线性动画 分组动画 Qt 动画是一种在 Qt 框架下创建交互式和引人入胜的图形用户界面的方法,我们可以认为是对某个基础元素的多个设置 主要动画元素 PropertyAnimation-属性值变化时的动画 NumberA…...

Lesson4-3:OpenCV图像特征提取与描述---SIFT/SURF算法
学习目标 理解 S I F T / S U R F SIFT/SURF SIFT/SURF算法的原理,能够使用 S I F T / S U R F SIFT/SURF SIFT/SURF进行关键点的检测 SIFT/SURF算法 1.1 SIFT原理 前面两节我们介绍了 H a r r i s Harris Harris和 S h i − T o m a s i Shi-Tomasi Shi−Tomasi…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...
