乐理-笔记
乐理笔记整理
- 1、前言
- 2、认识钢琴键盘及音名
- 3、升降号、还原号
- 4、如何区分同一音名的不同键?
- 5、各类音符时值的关系
- 6、歌曲拍号
- 7、拍号的强弱规律
- 8、歌曲速度(BPM)
- 9、附点音符
- 10、三连音
- 12、唱名与简谱数字
- 13、自然大调(白键)
- 14、自然大调(黑键)
- 15、自然小调
- 17、音程的基础概念
- 18、音程的属性(纯、大)
- 21、音的乐名
- 22、三和弦
- 23、七和弦
- 24、九和弦
- 25、挂留和弦
- 26、转位和弦
- 29、中古调式
1、前言
码农程序猿,爱好音乐,外表外向、内心内向的理想主义者,INFJ。喜欢吉他钢琴,好久不看乐理,加上上班摸会鱼,就整理一下,通俗易懂的句子都是。字都是自己打的,大老粗的感觉凑合看吧。
2、认识钢琴键盘及音名

软件上为什么不叫吉他窗?因为钢琴牛b。
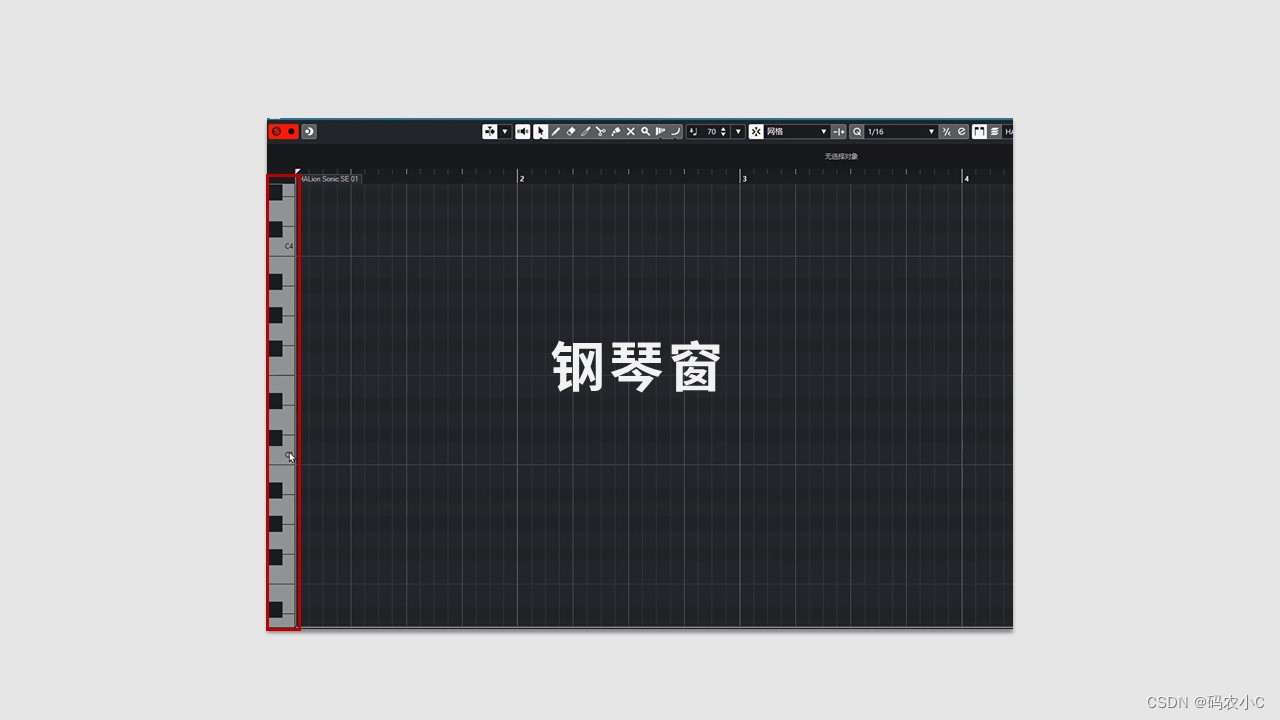
一般就88键够你用了。

分为七大组,一组都是一个CDEFGAB,对应1234567.

七个白五个黑为一组。
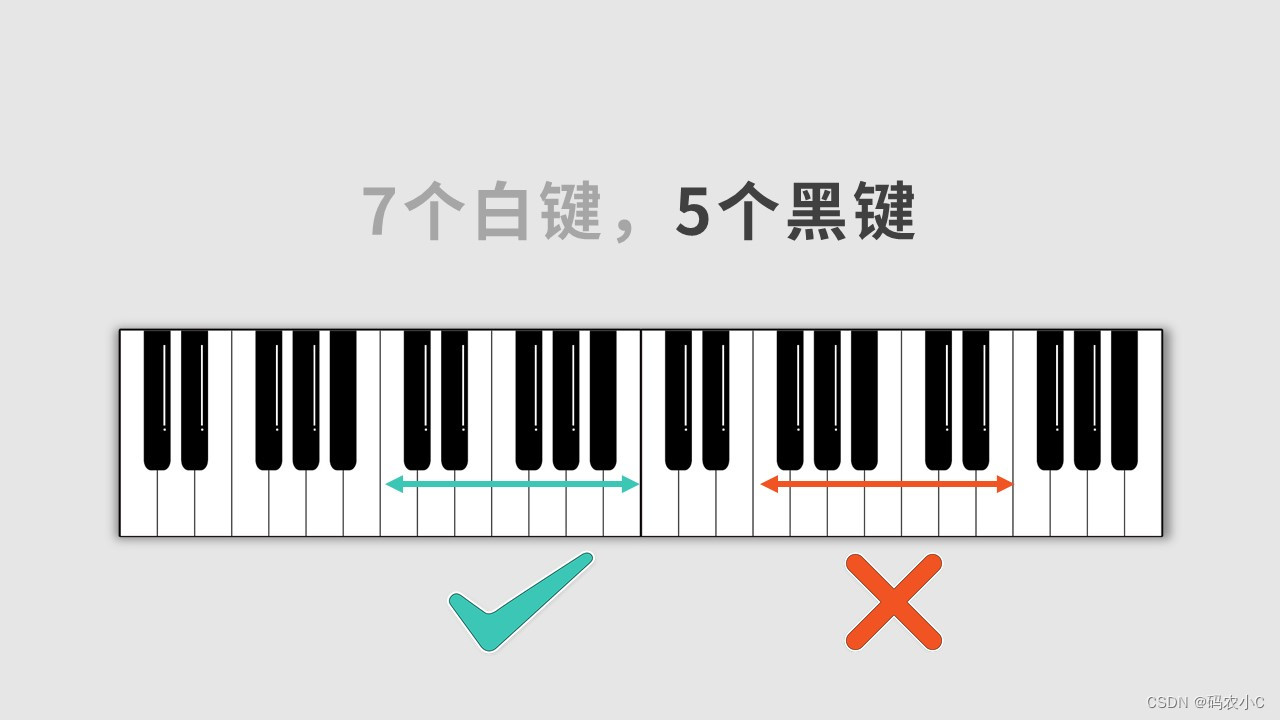
3、升降号、还原号
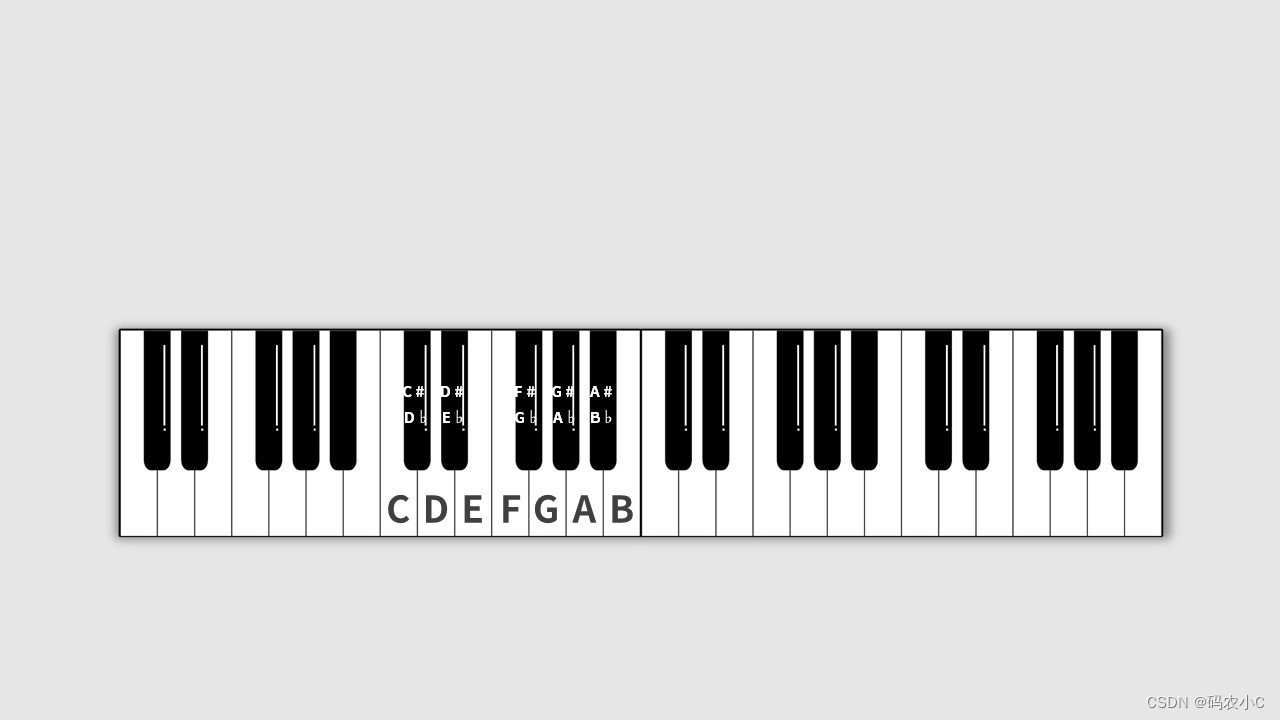
只有EF,BC之间是半音关系,因为他两个键是挨着的,中间没有隔黑键。
比如说CD之间隔了个黑键,C到黑键是半音,黑键到D键是半音,所以CD直接是全音。

两个白键之间的黑键是升左边的白键C#,也是降右边的白键Db。但是他俩不一样,不能画等号,因为有“还原键”的存在,因为还原一个是C,一个是D。
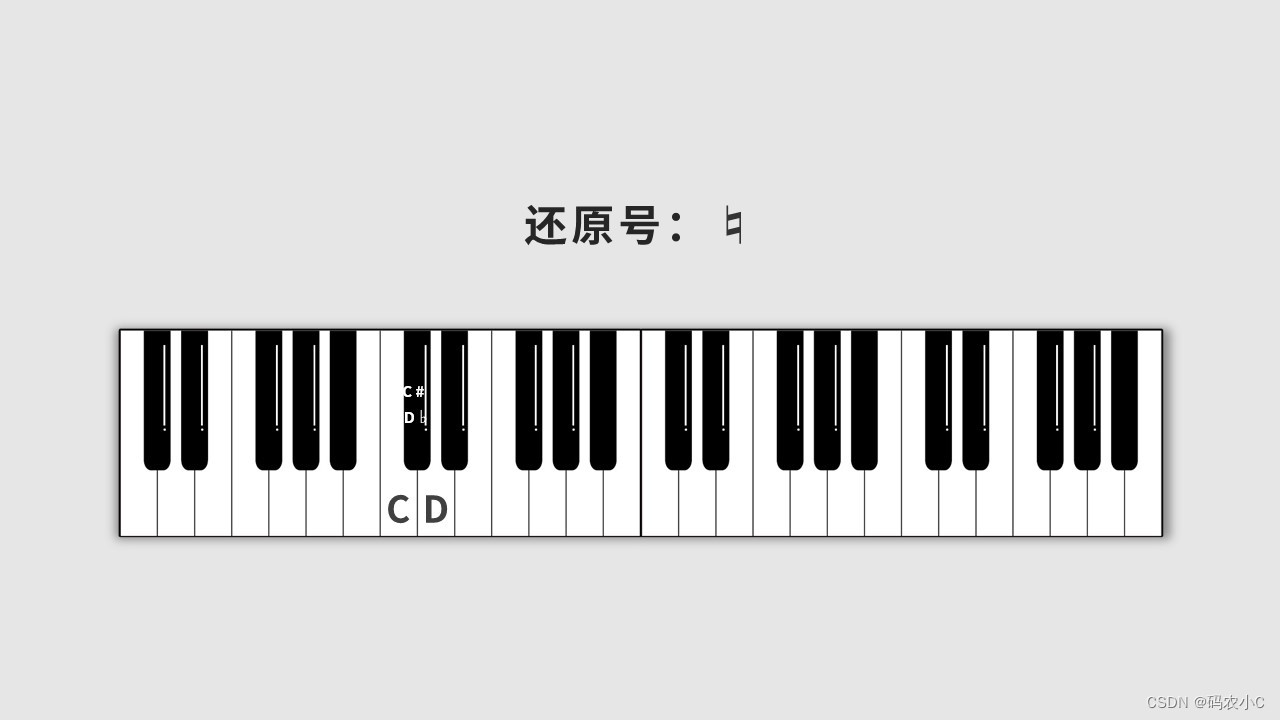
EF、BC之间没有黑键了,他俩之间是半音关系,所以E也是Fb(降F),F也是E#(升E)。所以B也是Cb(降C),C也是B#(升B)。
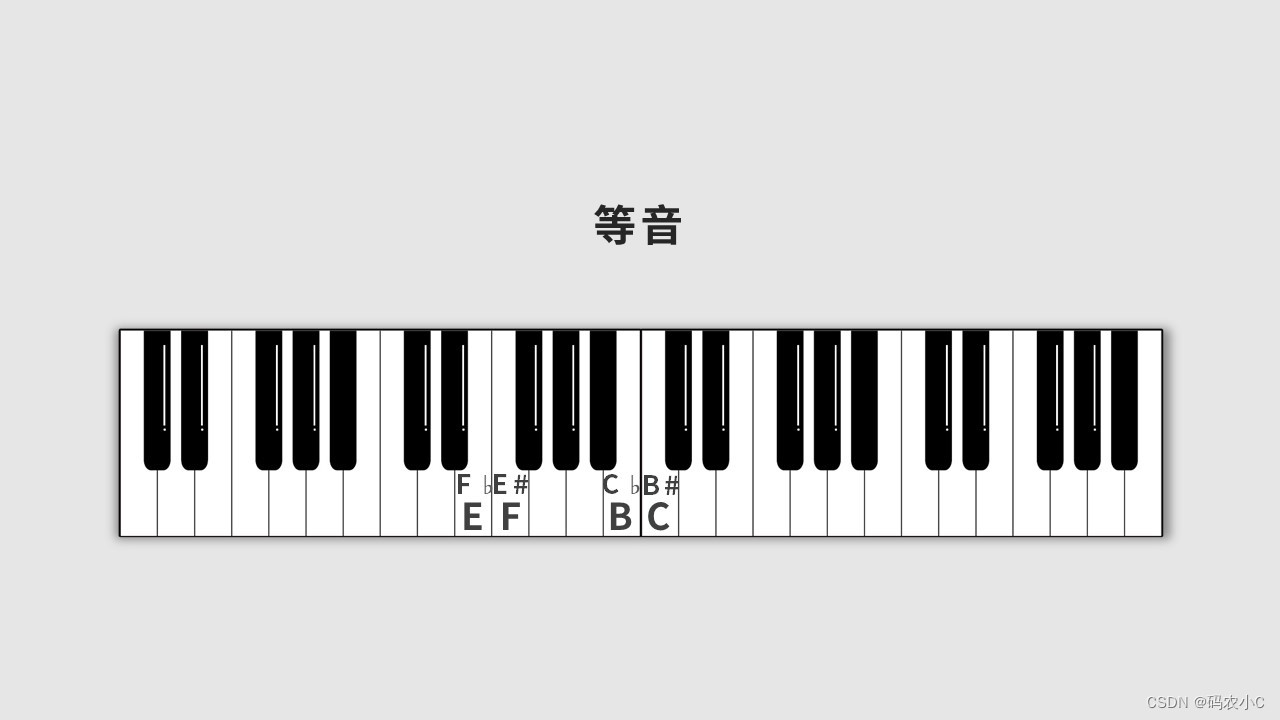
就是升了两个半音(一个全音),降了两个半音(一个全音),有点超纲,用到再说。

4、如何区分同一音名的不同键?
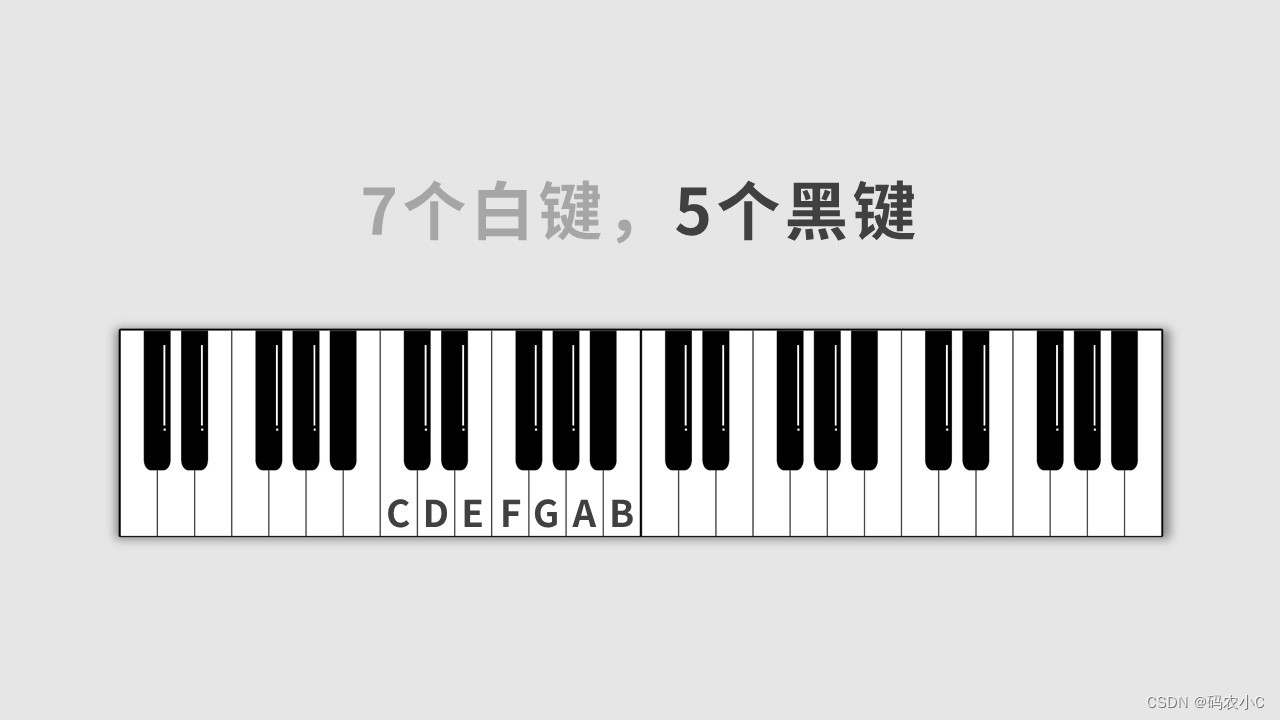
那就分组。。

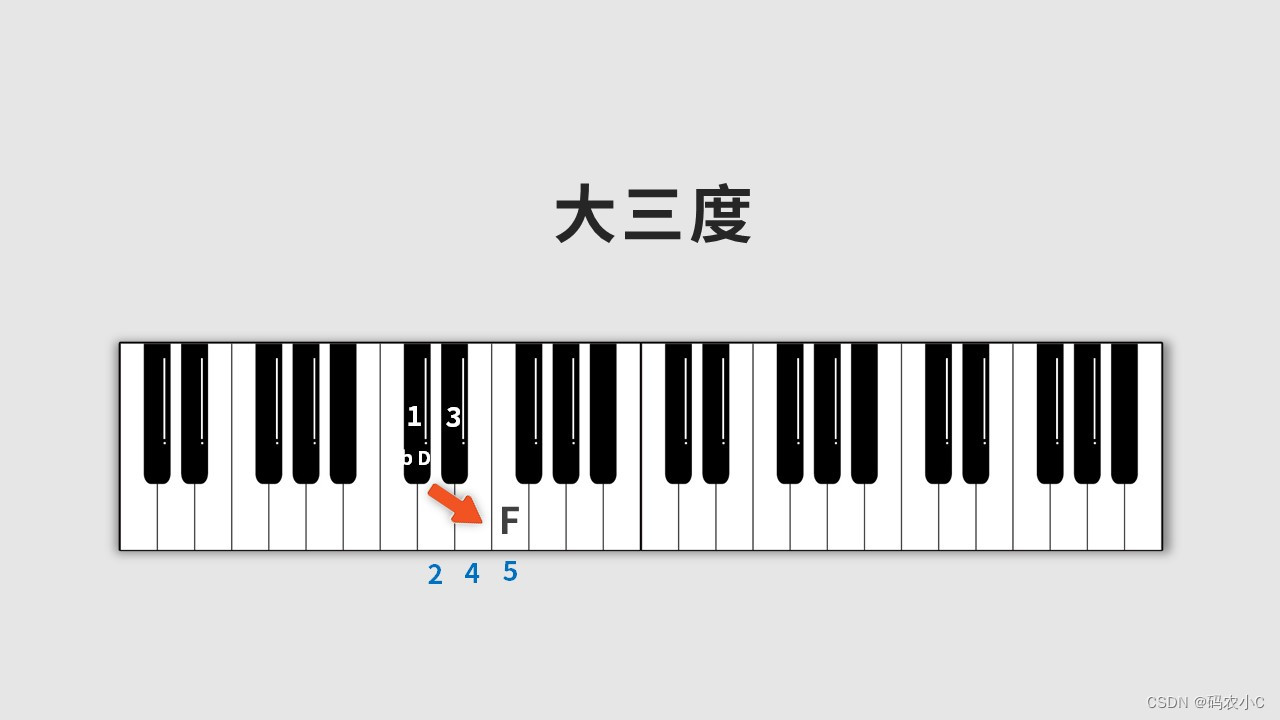
下边这个红色箭头就是d2

还有更简单的写法。

5、各类音符时值的关系
这里的X可以是1234567的任意一个。全音符的时值是二分音符的2倍,是四分音符的4倍。



6、歌曲拍号
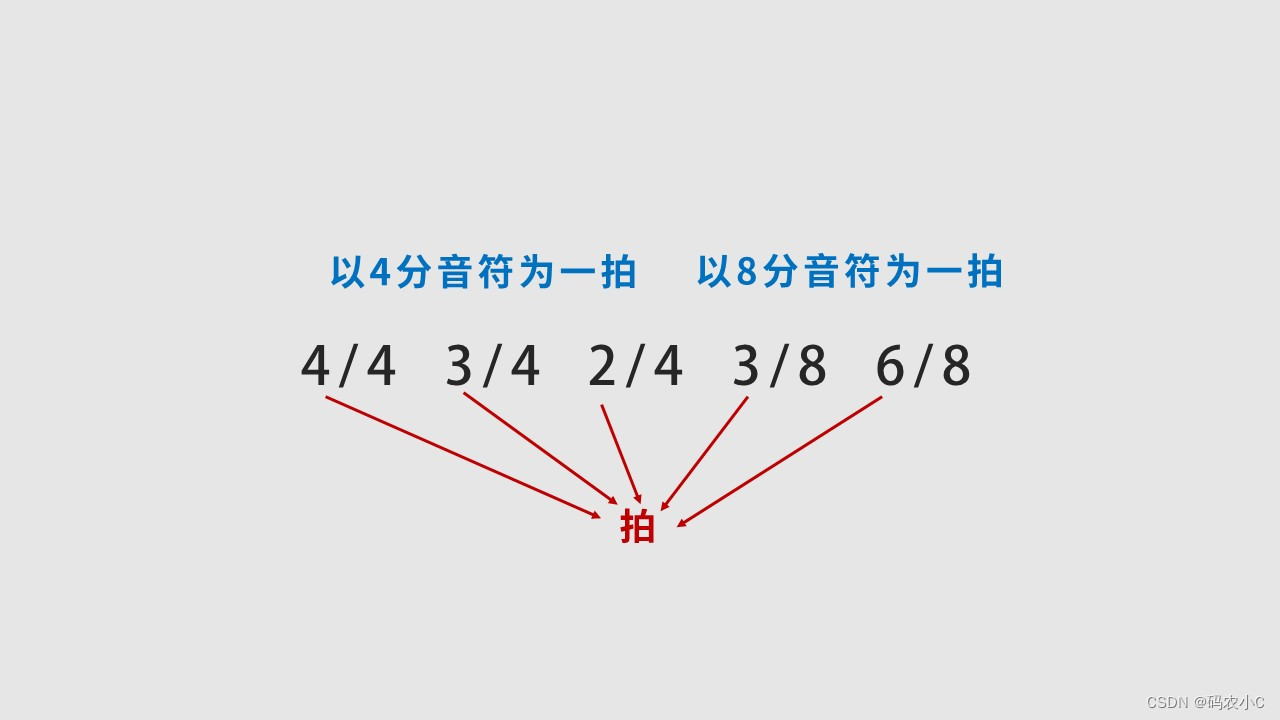
分母:以几分音符为1拍。
分子:每小节有几拍。
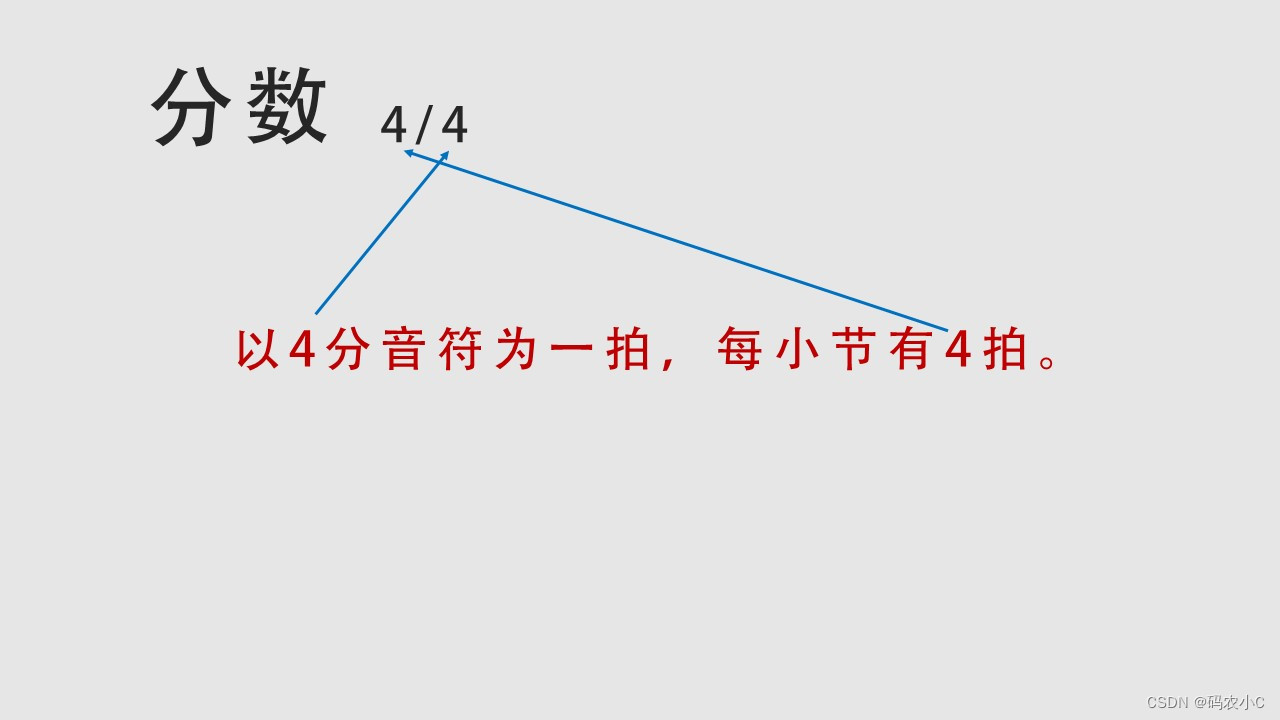
例如下图:分母:以4分音符为1拍。分子:每小节有4拍。

假如是4/4拍,全音符就是4拍,二分就是2拍,以此类推如下图。

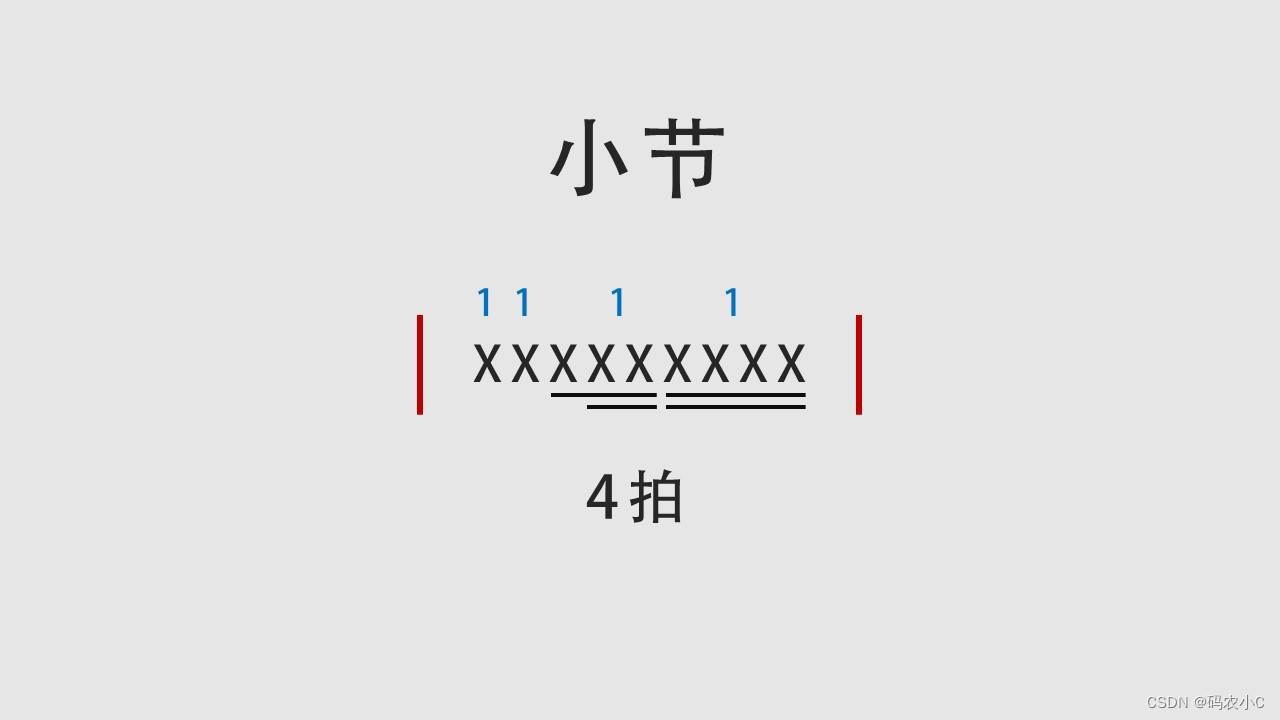
均等的,每一小节都是4拍。

下边这就是最常见的。4/4拍的一小节,每个都是全音符。


下边这是8个8分音符,也是4拍。因为以一个4分音符为1拍,一个8分音符就是半拍。

7、拍号的强弱规律
这个不是很重要,看看吧。
如何打拍子?



8、歌曲速度(BPM)



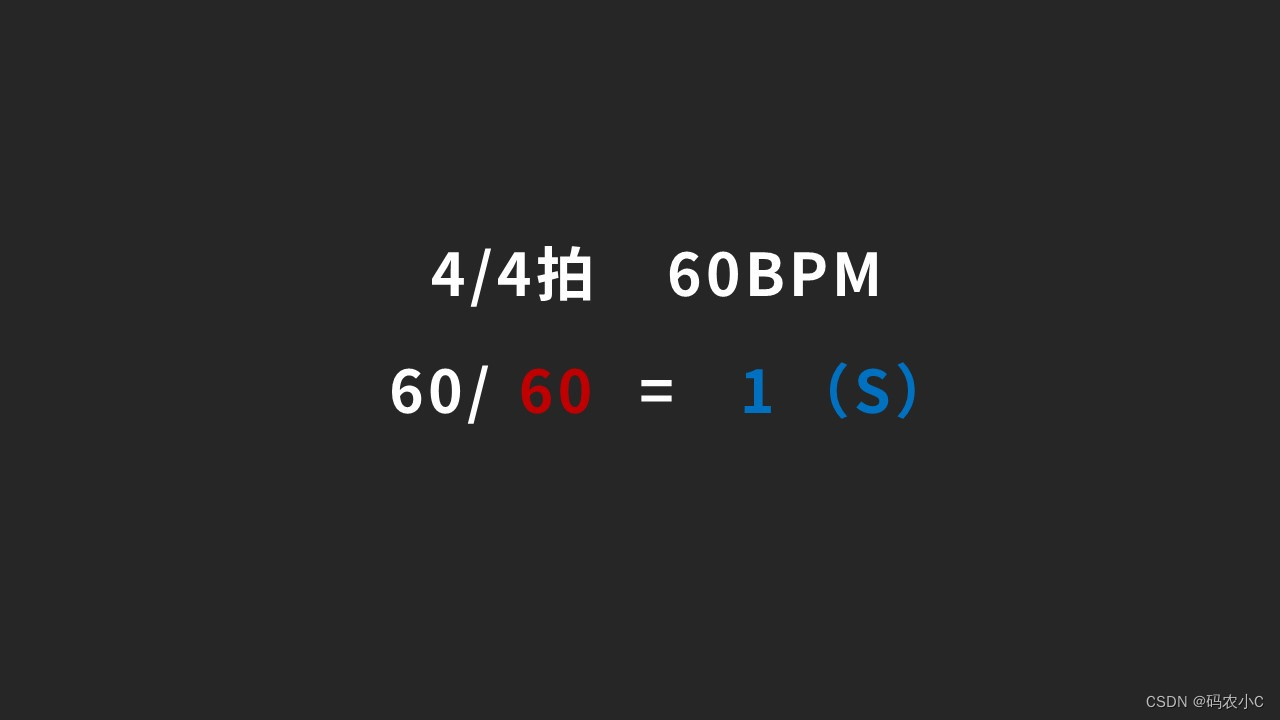
60BPM,每分钟60拍。

60BPM就是1秒一拍。
下边就是以一个8分音符为1拍,120BPM就是0.5秒一拍。



9、附点音符
在原本音符的时值基础上,加上(延长)原本音符的一半。

在原本4分音符的时值基础上,延长4分音符的一半,也就是8分音符,相当于加个8分音符。


表示形式如下:

10、三连音
先记住 :三代二,三连音的总拍数代表其下方两个常规音符的总拍数。

下边是四分音符的三连音。

一个四分音符的三连音等于一个二分音符。
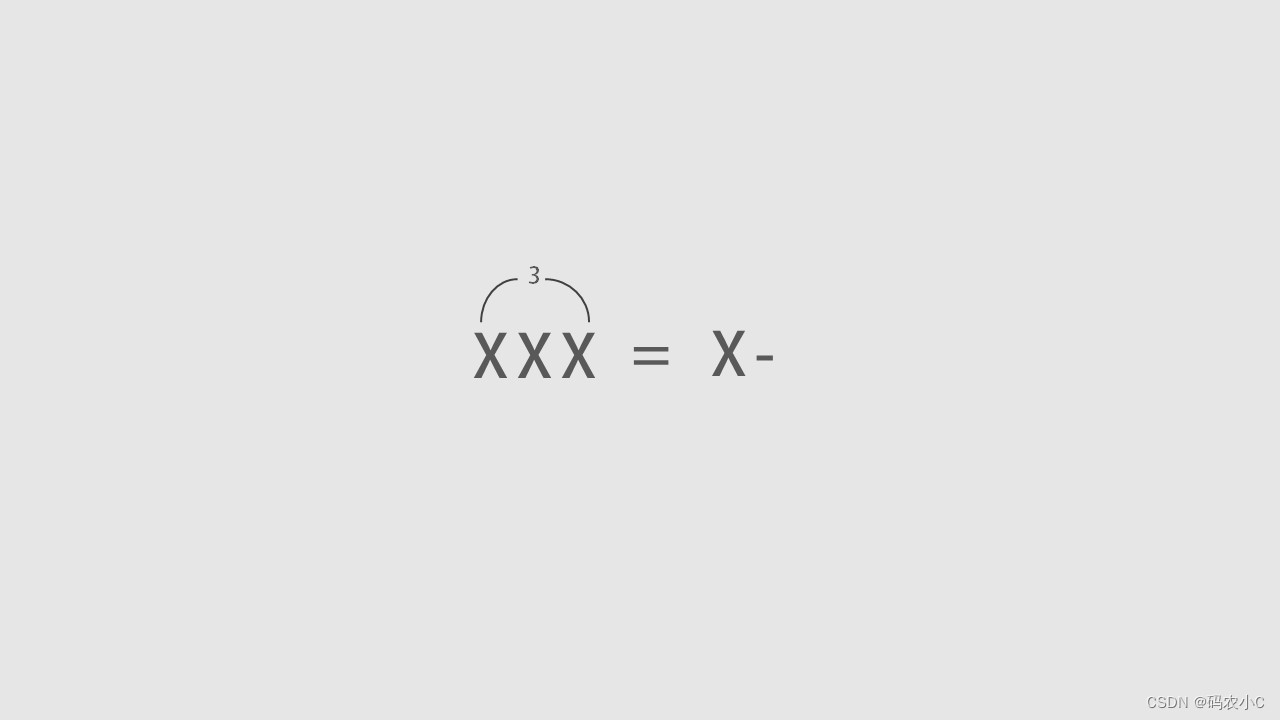
一个四分音符拆为一个八分音符的三连音。总拍数为1拍。
三代二:三连音的总拍数代表其下方两个常规音符的总排数。
比如下方这个三连音,3个拿出俩,两个八分音符为1拍,所以总拍数是1拍。
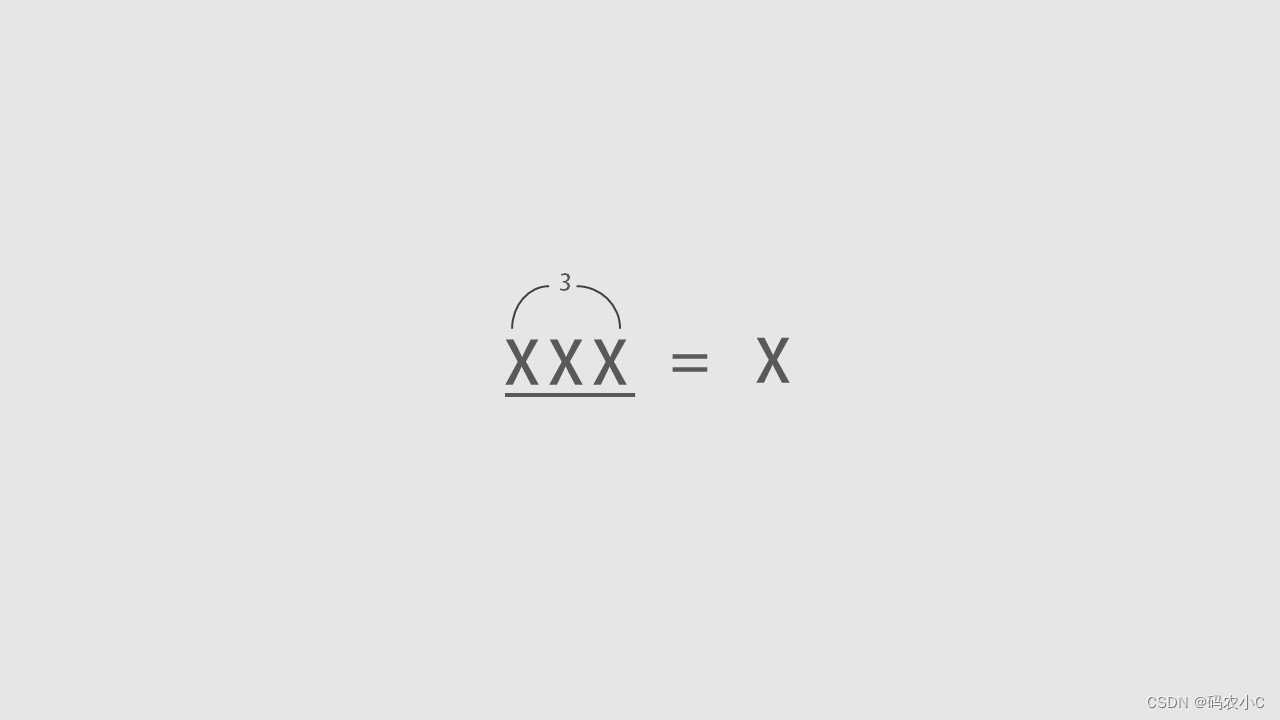
12、唱名与简谱数字
CDEFGAB不一定对应1234567,但是唱名一定对应1234567。
CDEFGAB只有在1=C时对应1234567。

上边加1个点,高1个八度。加2个点,高两个八度。

13、自然大调(白键)
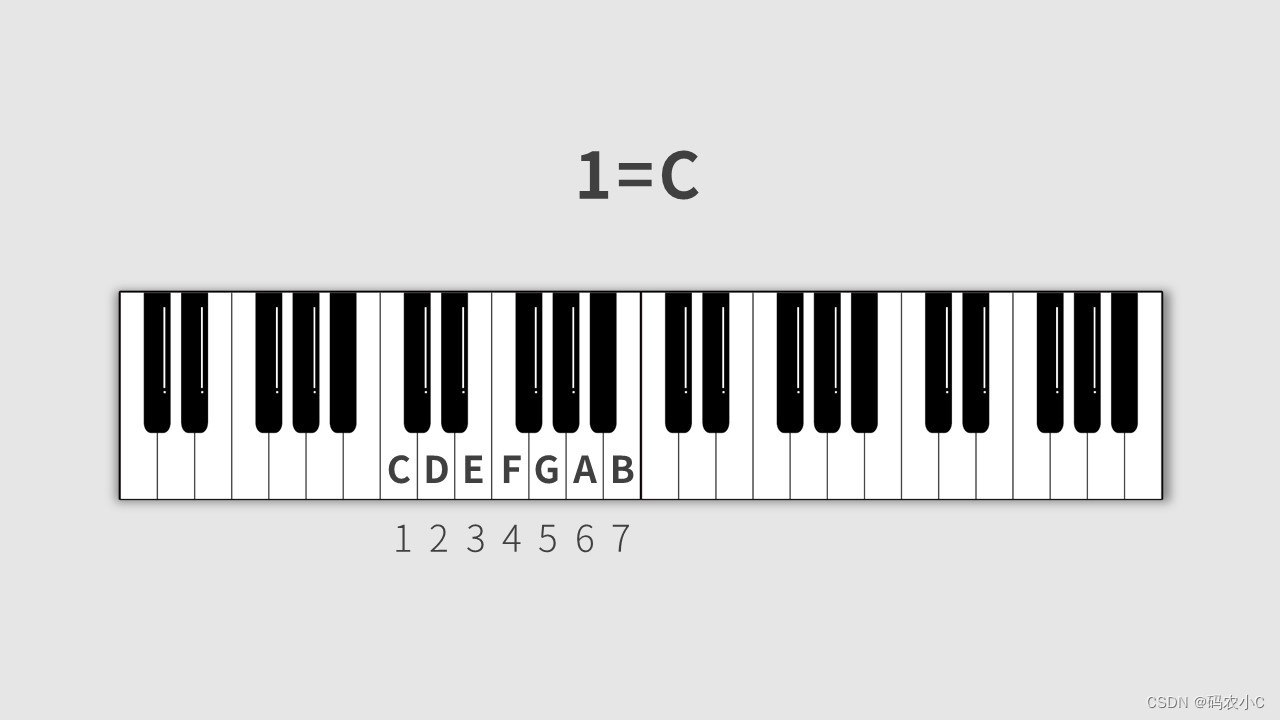
也就是1=c,内部不管哪个八度规律都是一致的。

记住下边的:全全半全全全半 ,因为后边的G、D大调都可以用此口诀来推断。
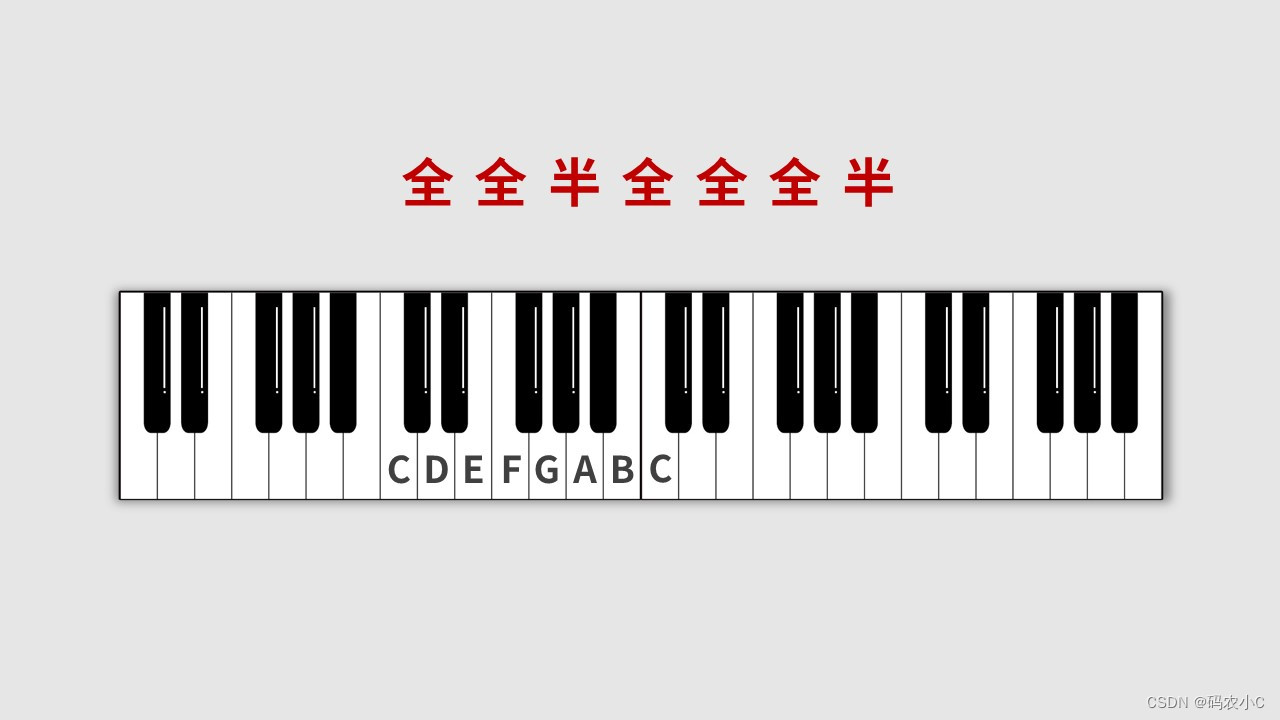
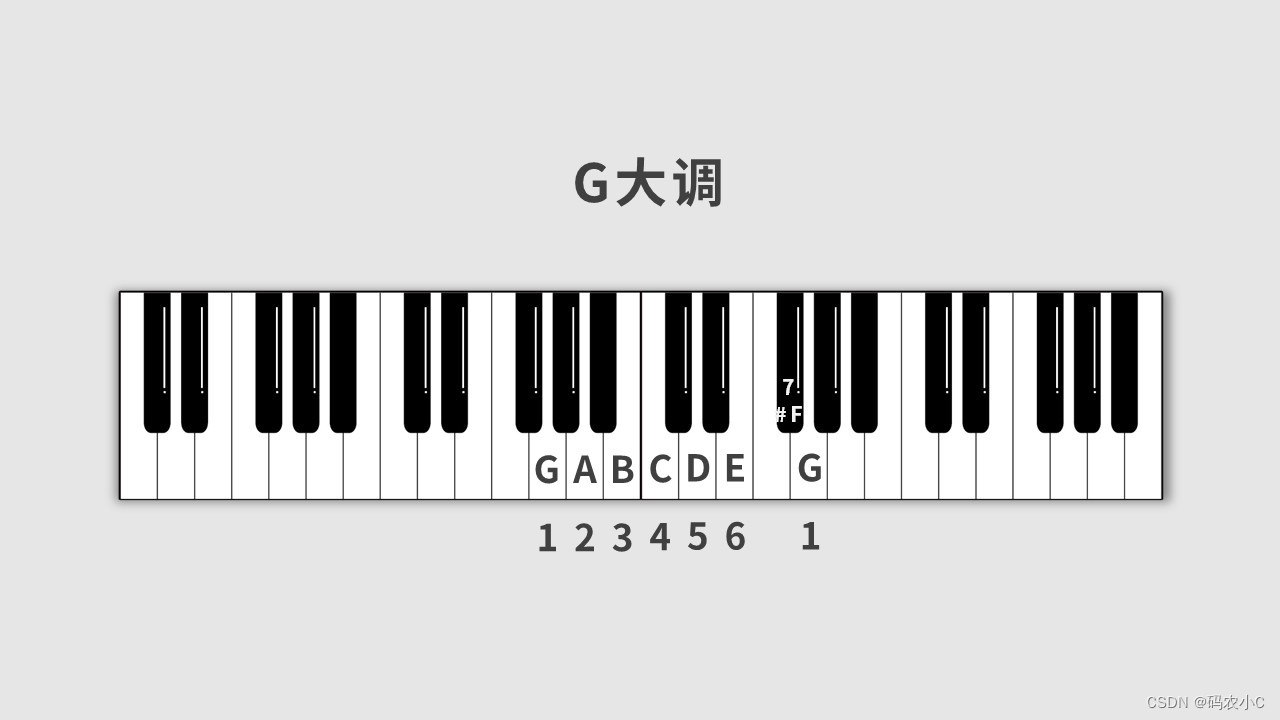
根据:全全半全全全半来推导下边的G大调,1=G,G后接一个全音是A,A接一个全音是B,B接一个半音是C,C接一个全音是D,D接一个全音是E,E接一个全音是升F(#F),#F接一个半音是G。
注意:为什么#F不用降G?因为要求七个音名按顺序依次出现。
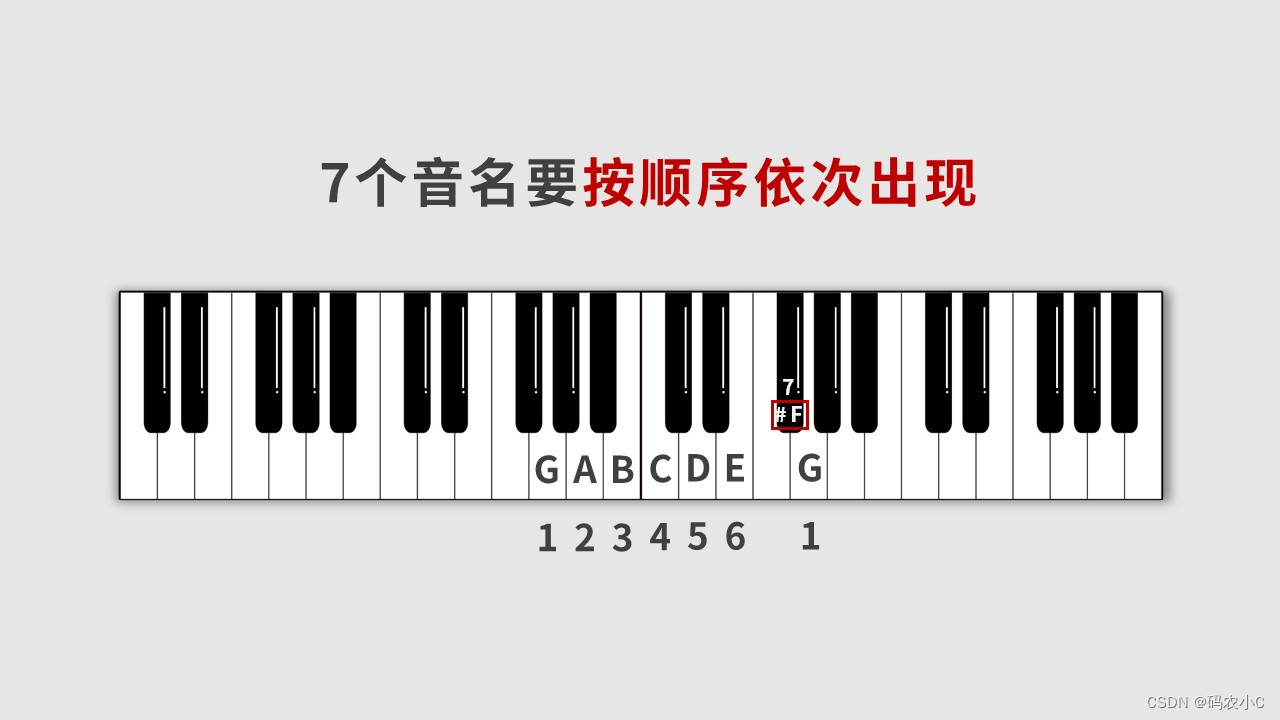
同理根据:全全半全全全半 来推到D大调。
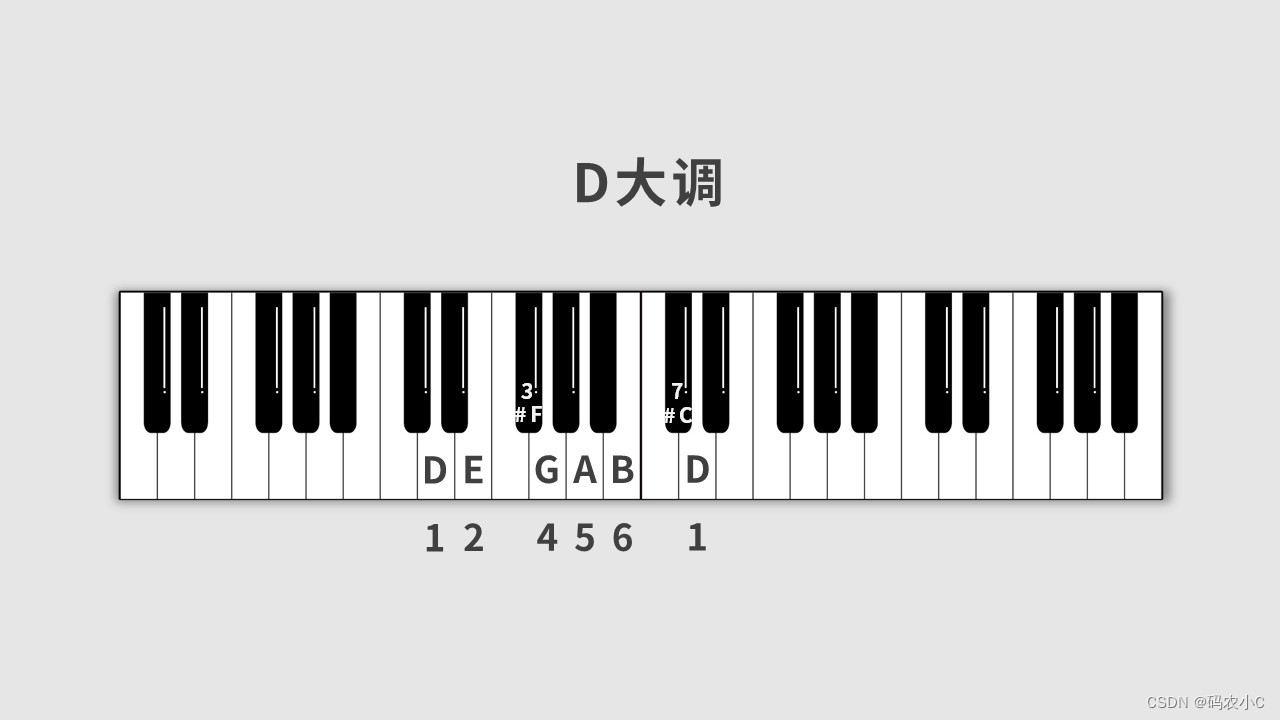
14、自然大调(黑键)
上节都是从白键出发的,也可以从黑键出发。
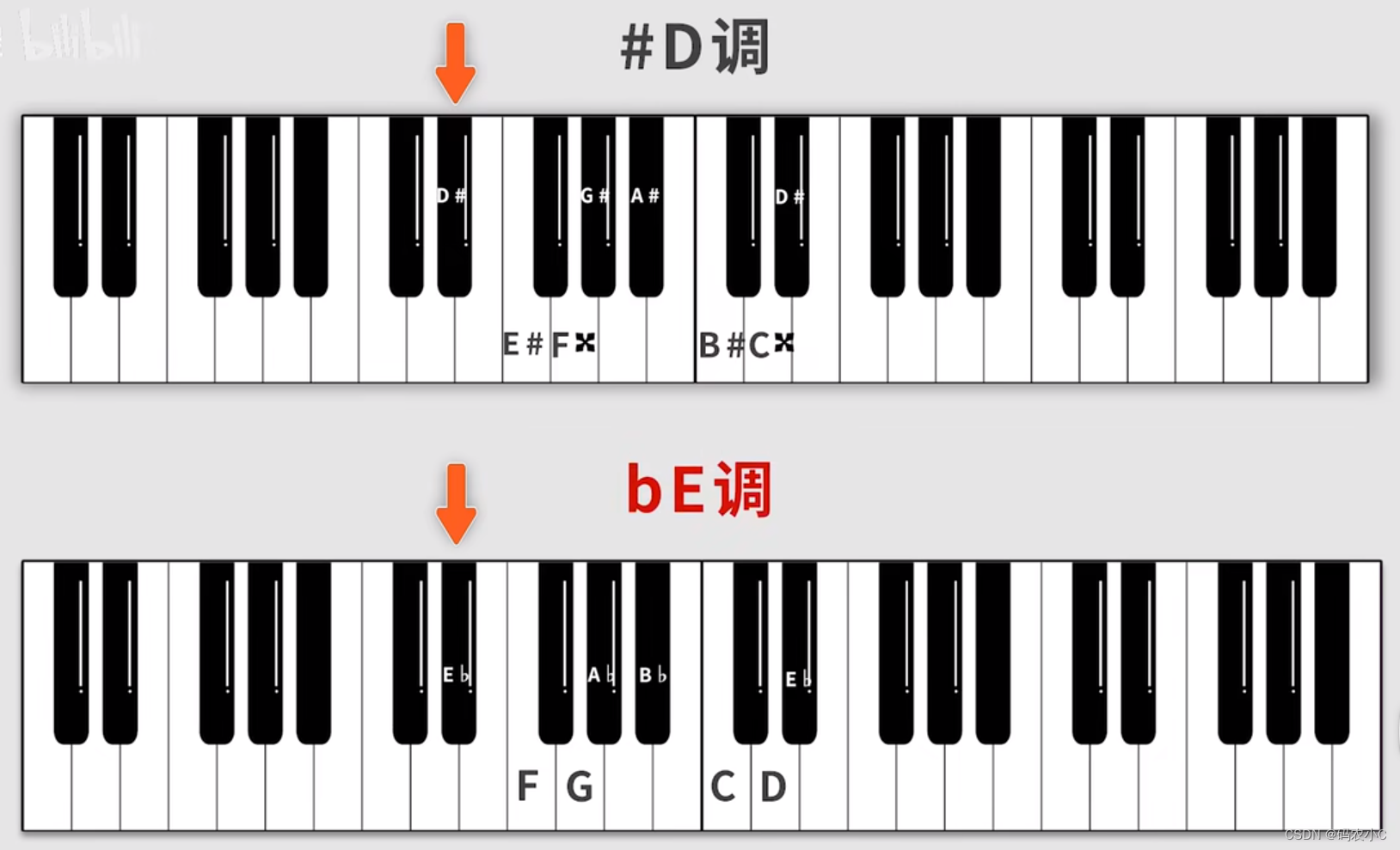
黑键没有自己的音名,它的音名是通过左右白键升或者降得来的,在以黑键为开始时,通常用降x来表示,因为降比升容易表示,看下边解释。
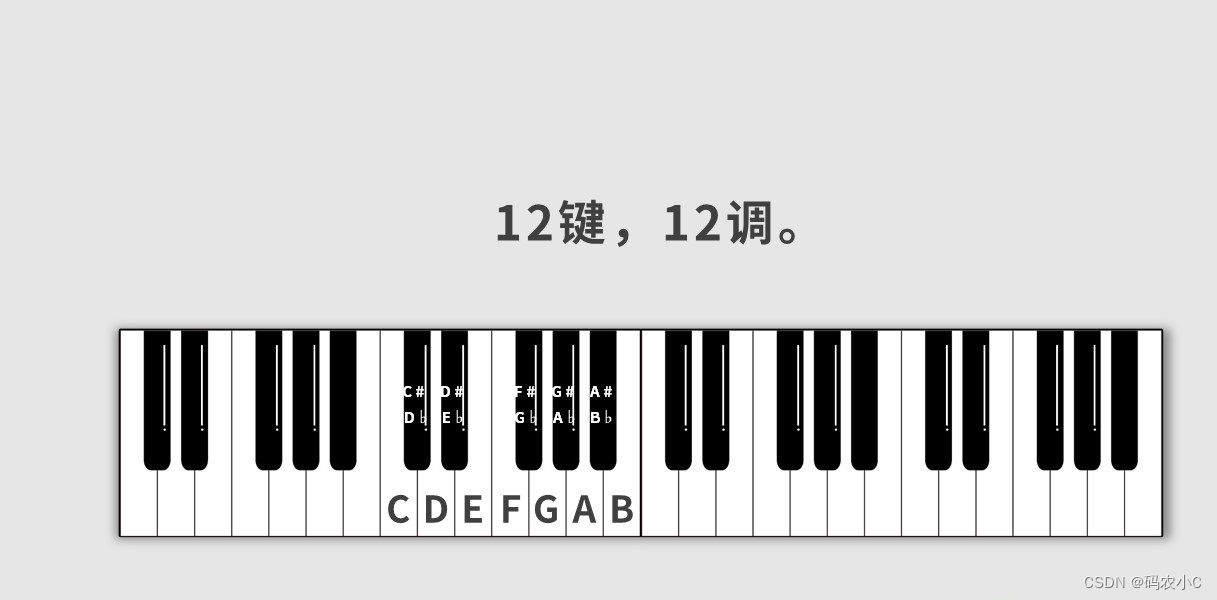
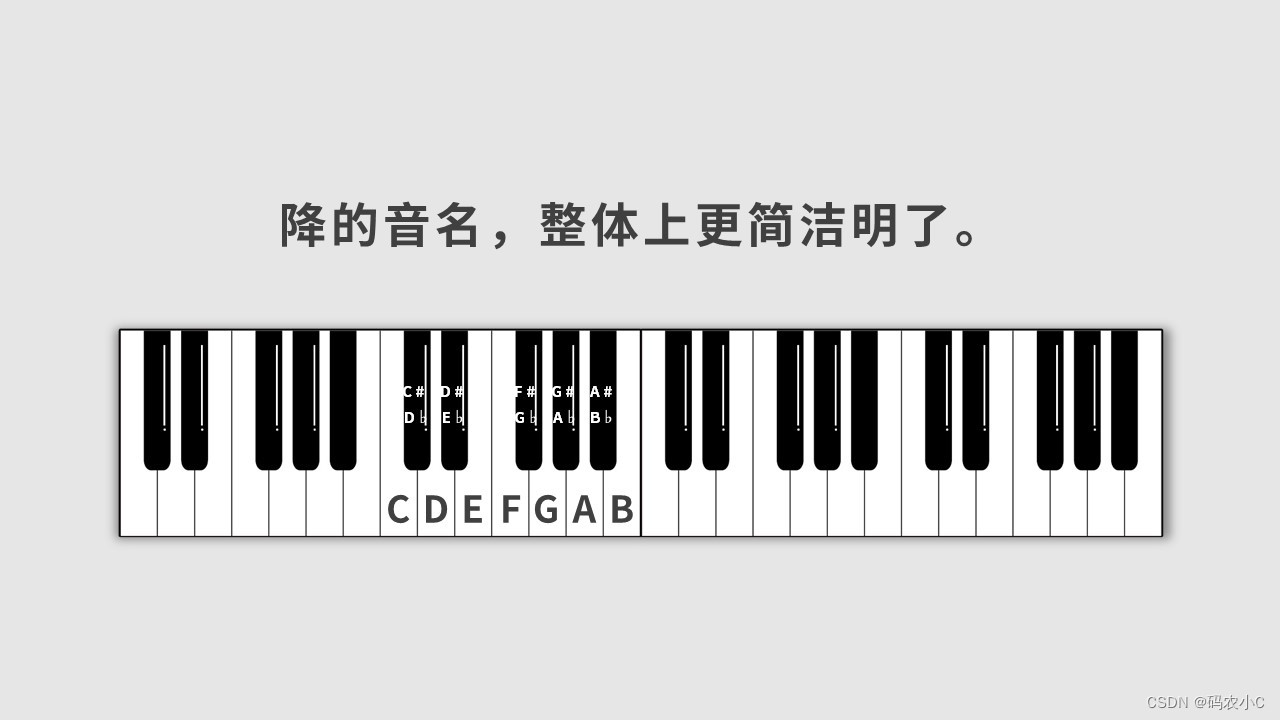

例如升C和降D都是一个,但是降D(bD)简单。看下边
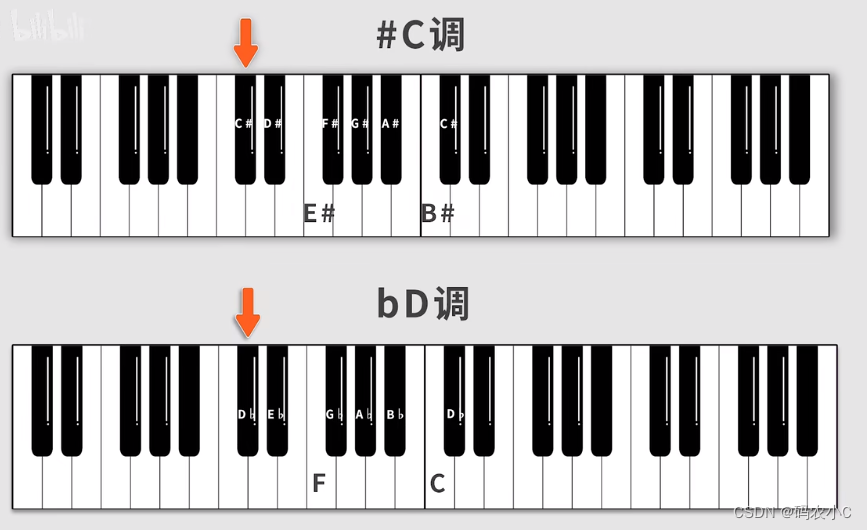
再举个例子,升D和降E都代表同一个黑键,但是降E的写法简单。
15、自然小调

记这个太麻烦:全半全全半全全

可以通过小调找出来它的关系大调。(先往后推一个全音一个半音,找到大调对应的音阶,再把大调最后的两个音阶移动到最前边,准确的说是移动67)

比如说:A小调,找它的关系大调,向后一个全音一个半音,就是C,C对应的音阶为:CDEFGAB,把AB再挪到最前边就是A小调的音阶-ABCDEFG。步骤如下:
1、找A的关系大调:
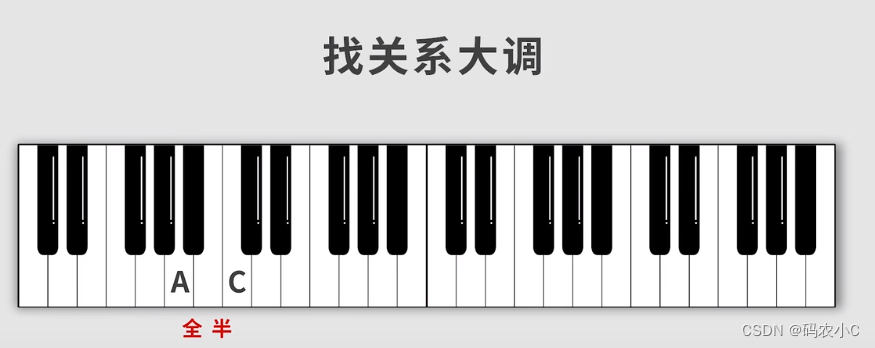
2、找对应C大调的音阶:
3、对应大调的最后俩挪到前边(准确的说是移动67两个到前边)就是小调对应的音阶:
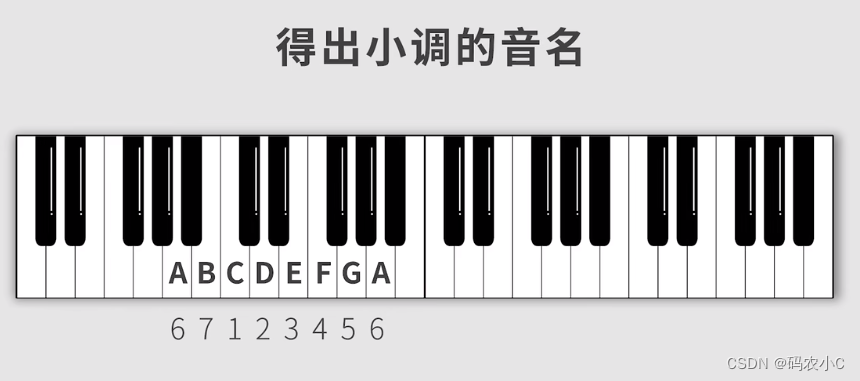
同理再来一个例子:E小调的
1、找E小调的关系大调是G(往后一个全音,一个半音)
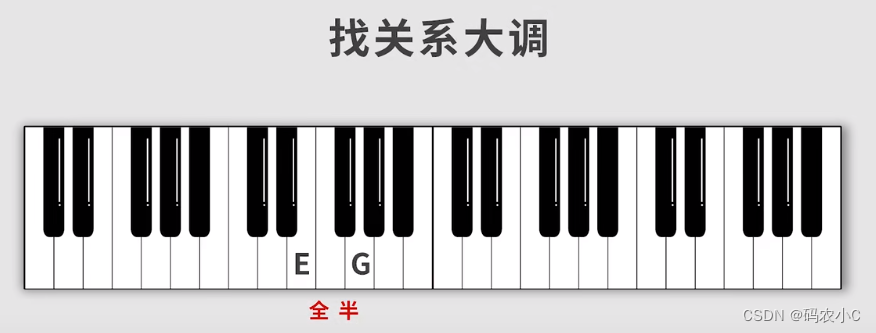
2、写出对应G大调的音阶
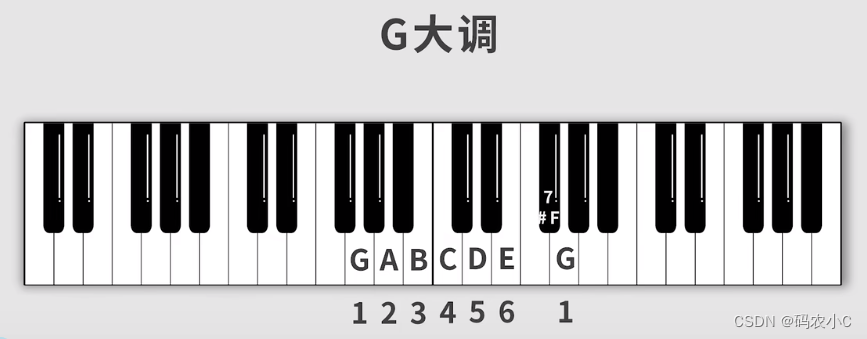
3、对应大调的后边俩挪到前边(准确的说是移动67两个到前边)就是E小调的音阶。
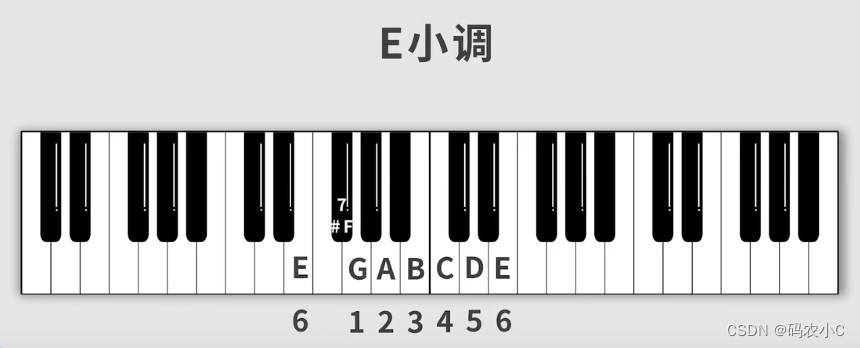
再来卡一个:D小调
1、找对应的大调为F(往后一个全音,一个半音)
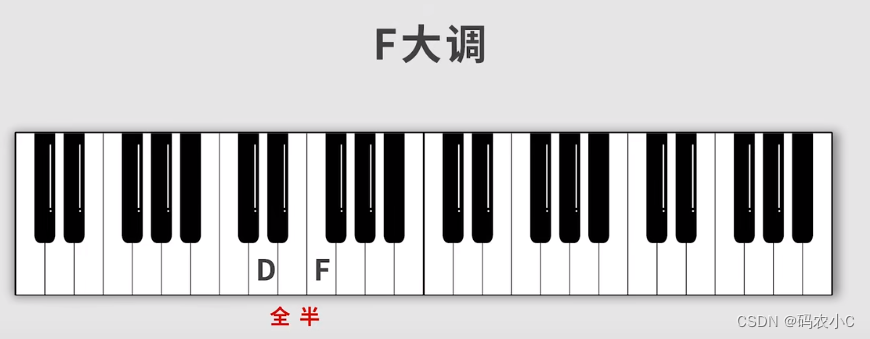
2、找出对应大调F的音阶:
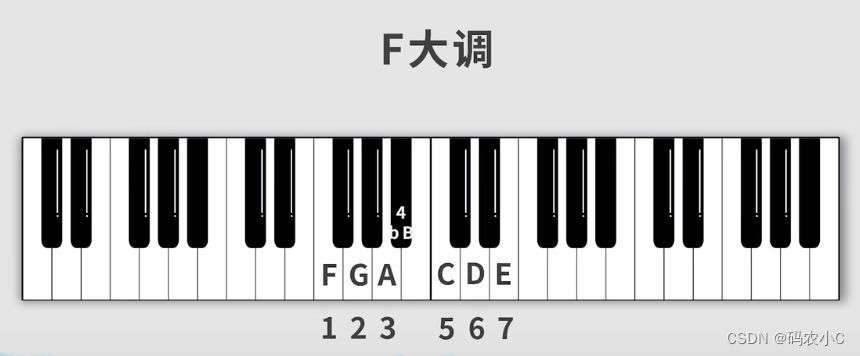
3、移动:(准确的说是移动67两个到前边)
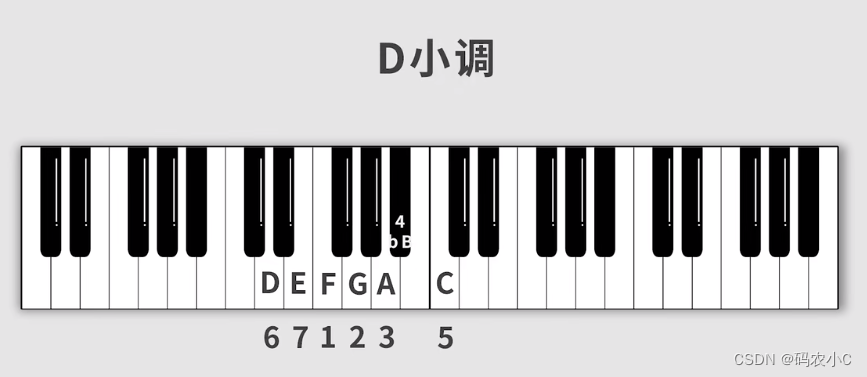
17、音程的基础概念
音程:音与音之间的距离,单位是度。
比如说C-A有几度?他俩之间有几个白键就有几度,包含他俩所在位置的白键。

有几个白键就有几度,但是要注意是包含他俩所在位置的白键。
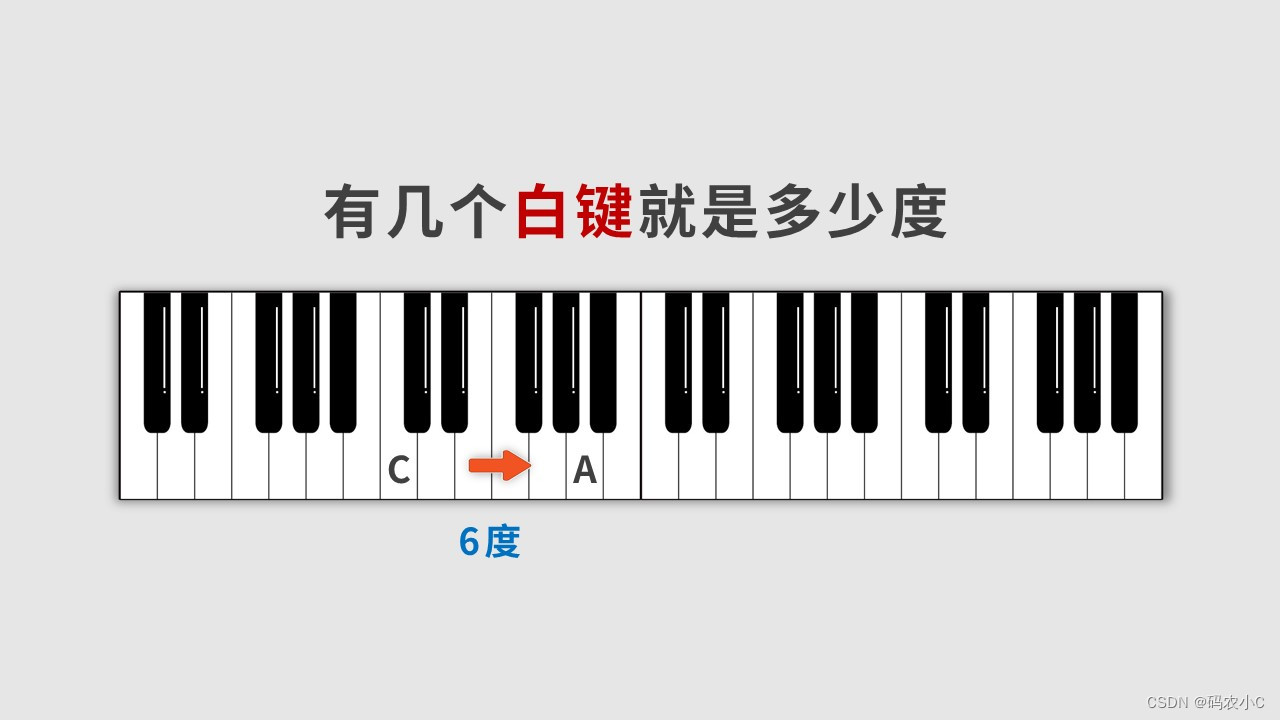
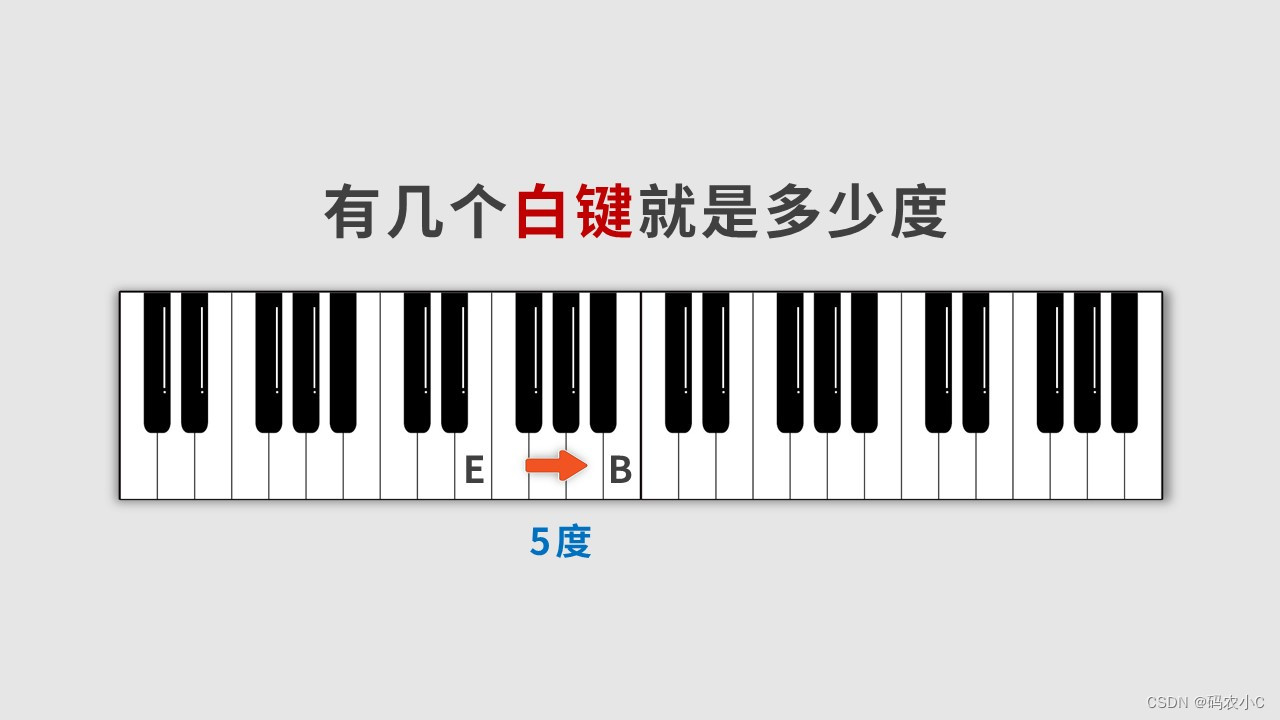
那么下边的黑键之间有几度?要先还原黑键,再数,不通过写法还原时数出的是不一样的,升d就往左还原,同一个位置降E就要往右还原,所以同一个位置不同写法(D#、Eb)输出的度是不一样的
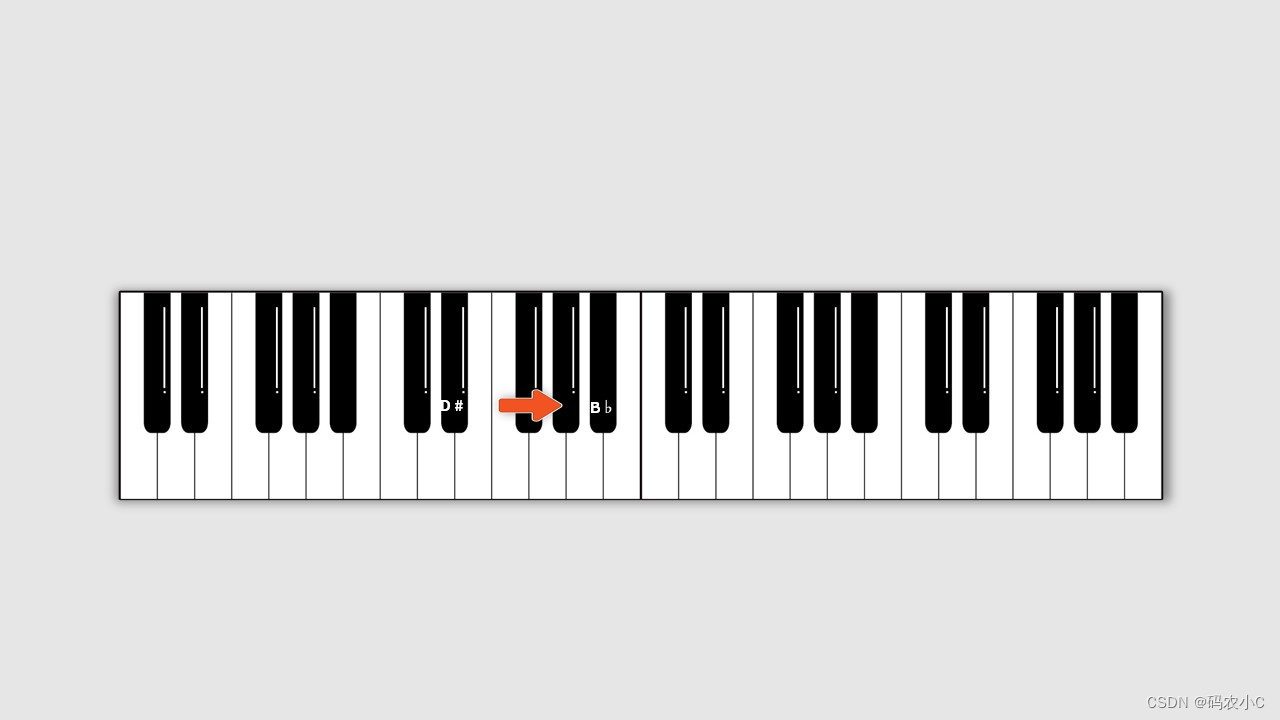
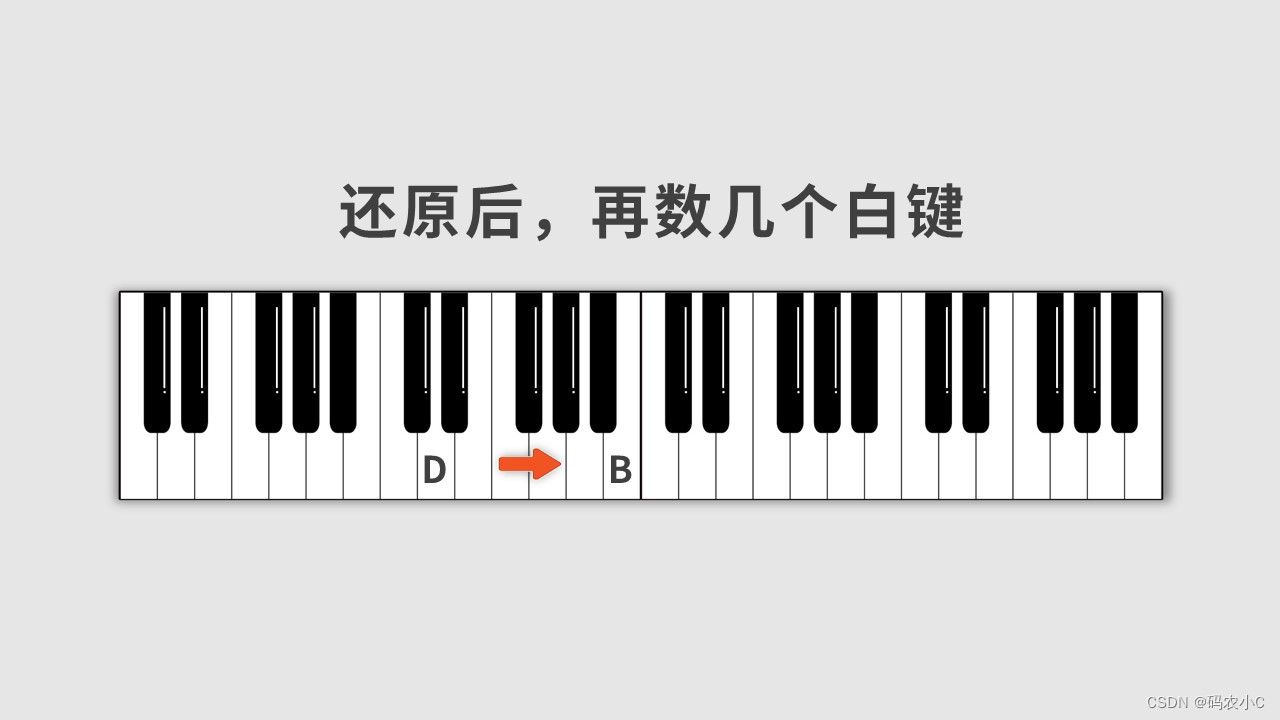
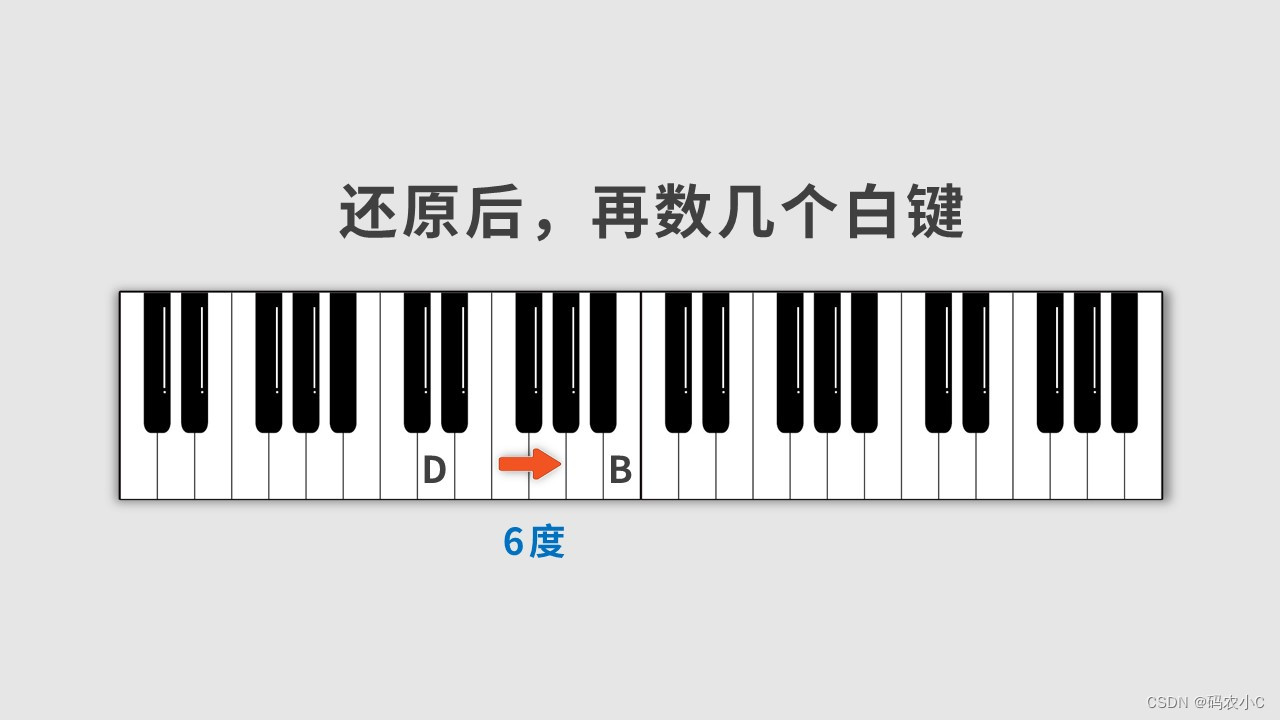
举例:C#到E有几度?先还原到C,再数就是3度。

Db到E有几度?先还原到D,再数就是2度。

18、音程的属性(纯、大)

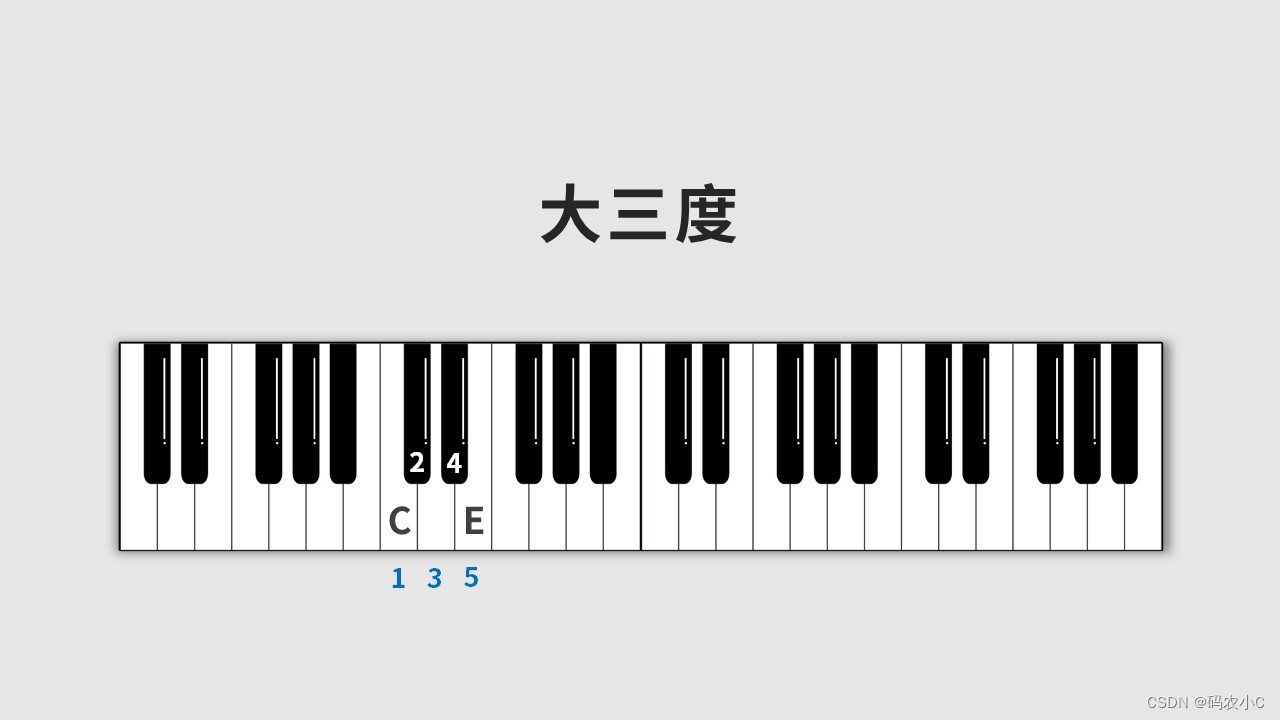
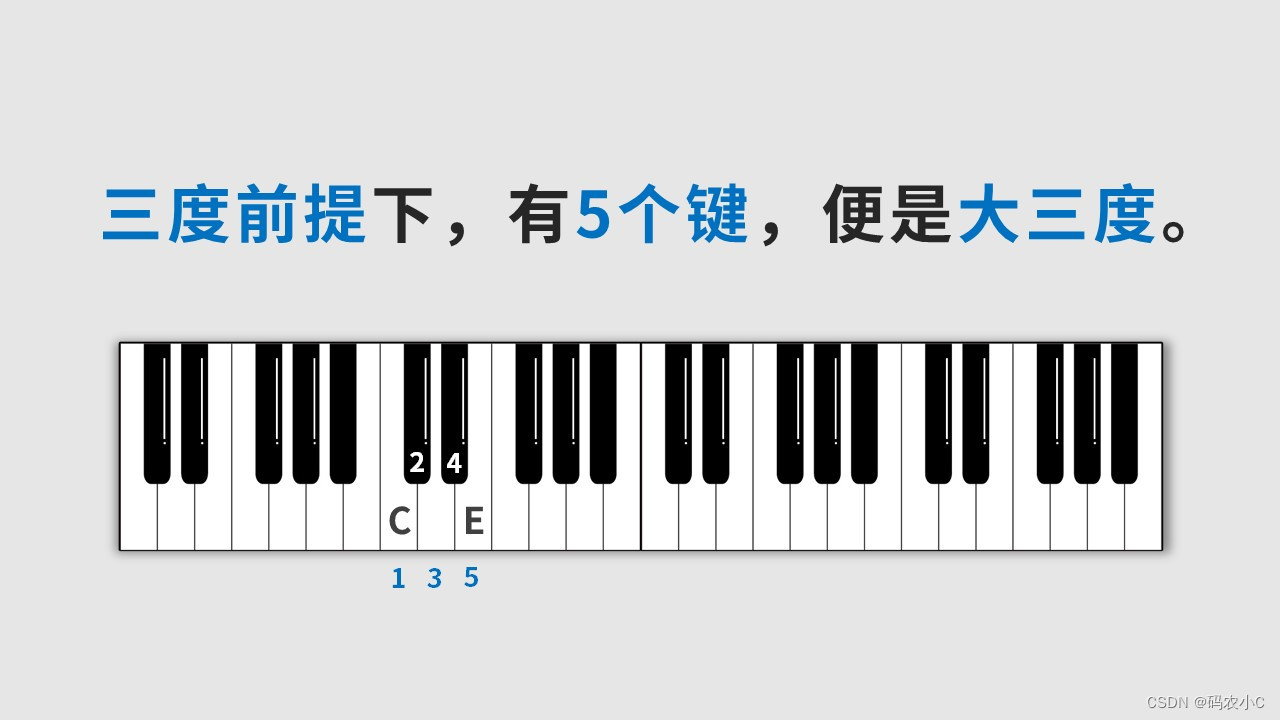
21、音的乐名

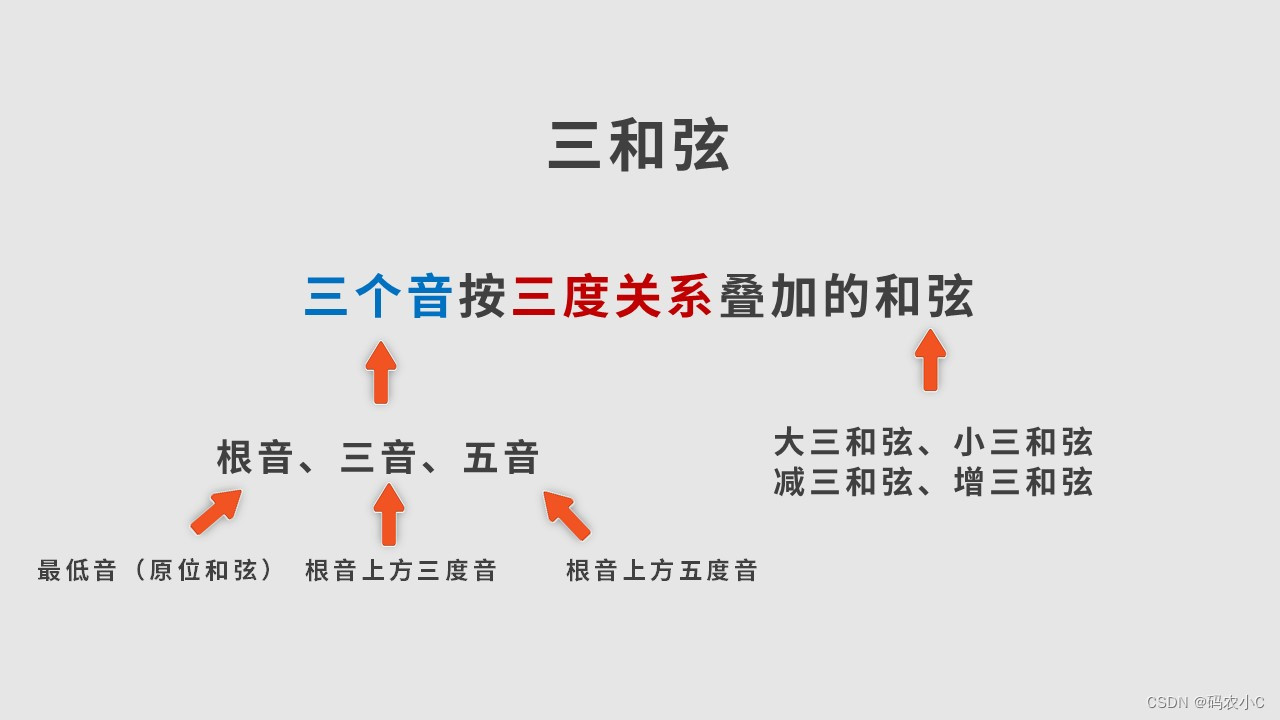
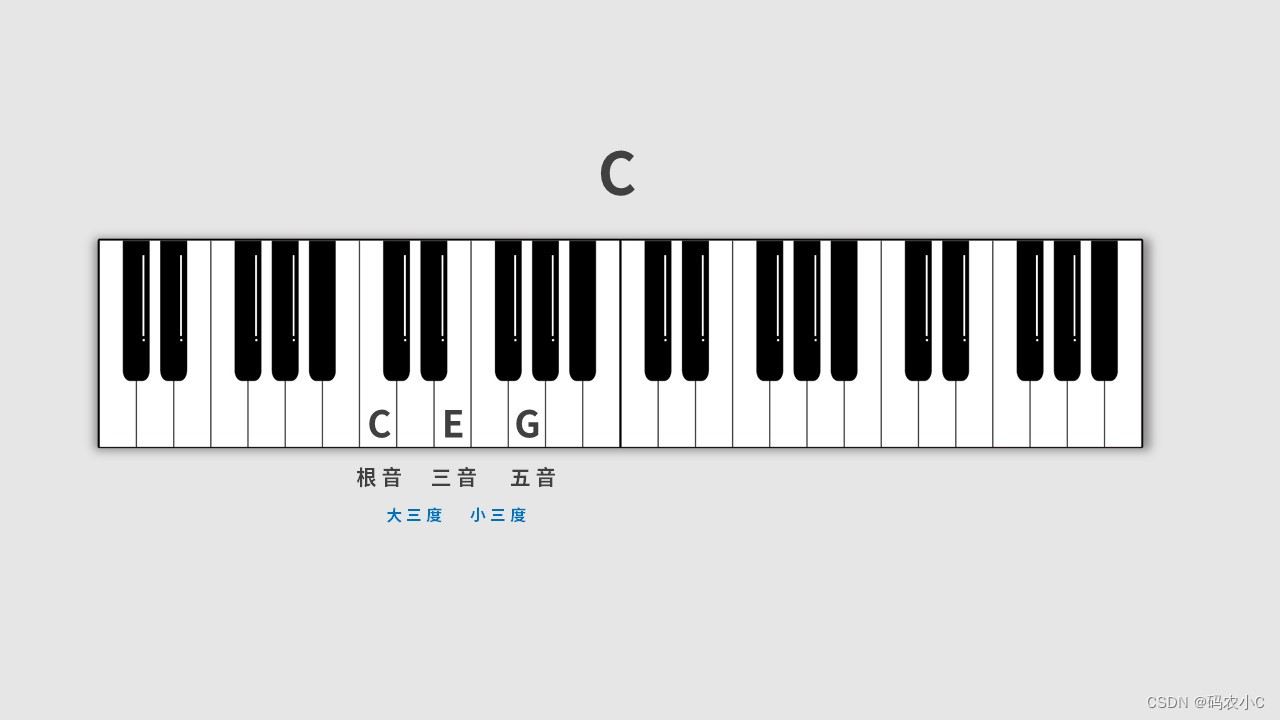
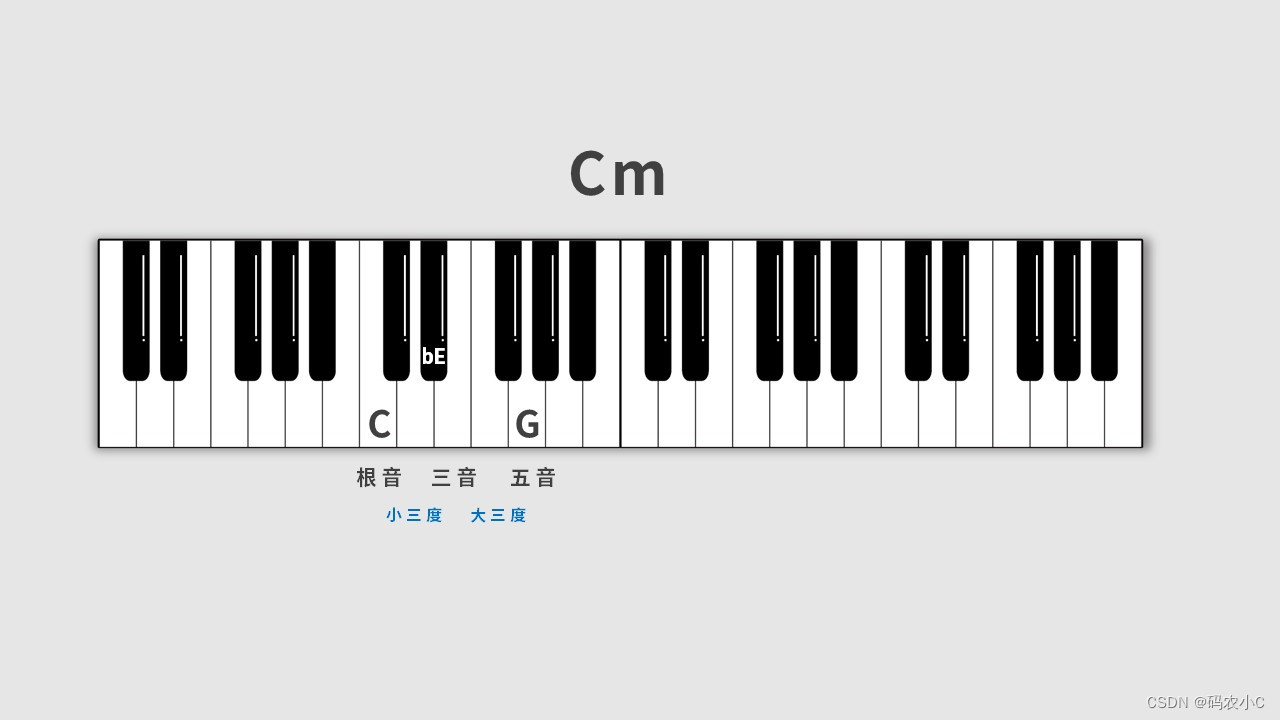
22、三和弦




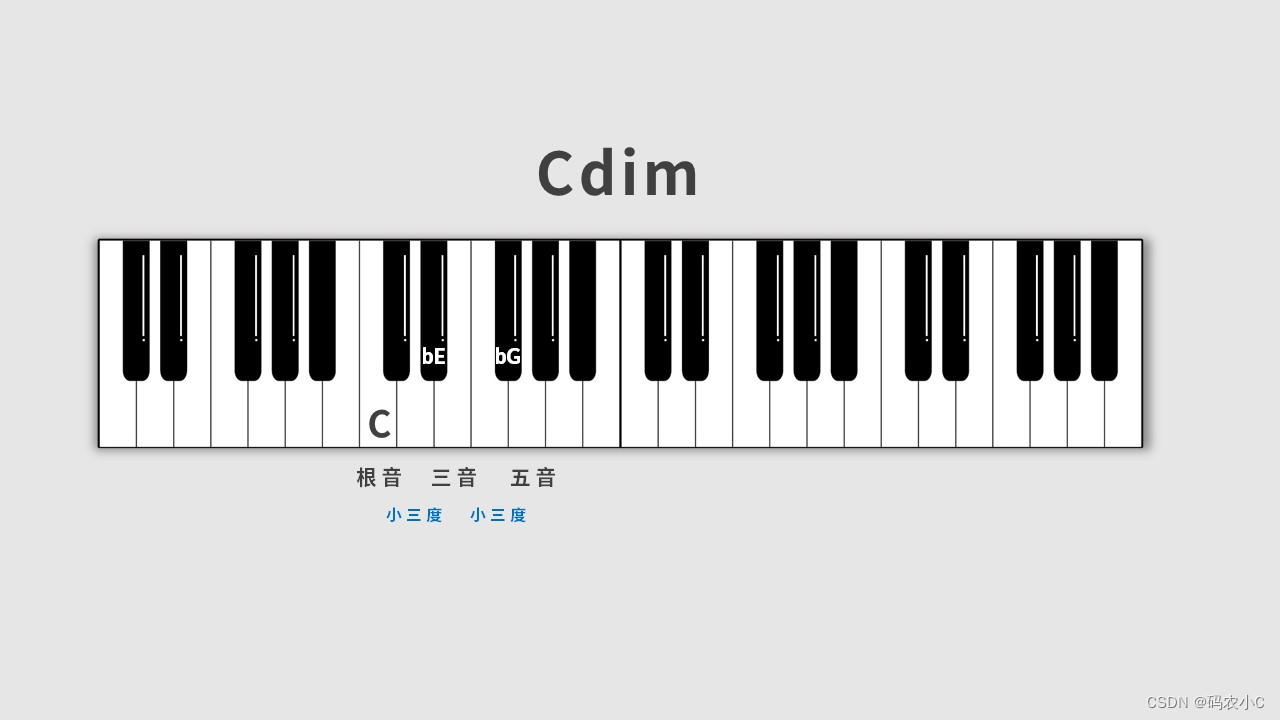

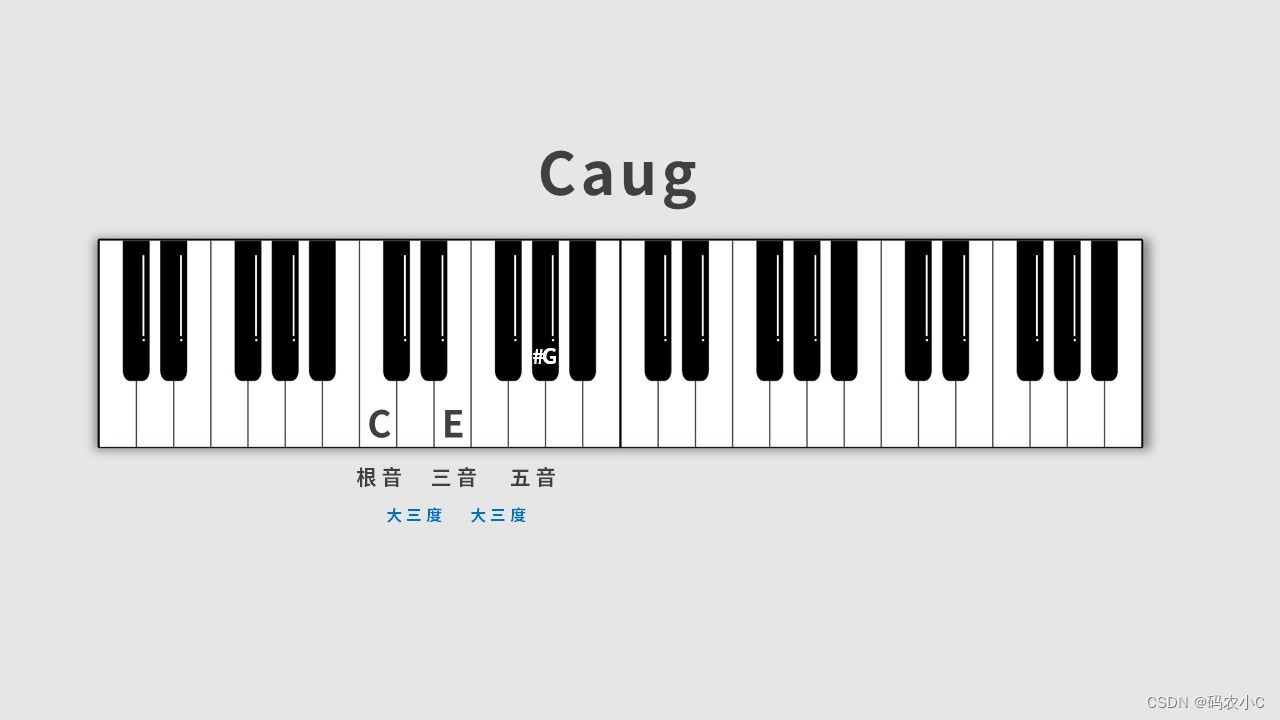
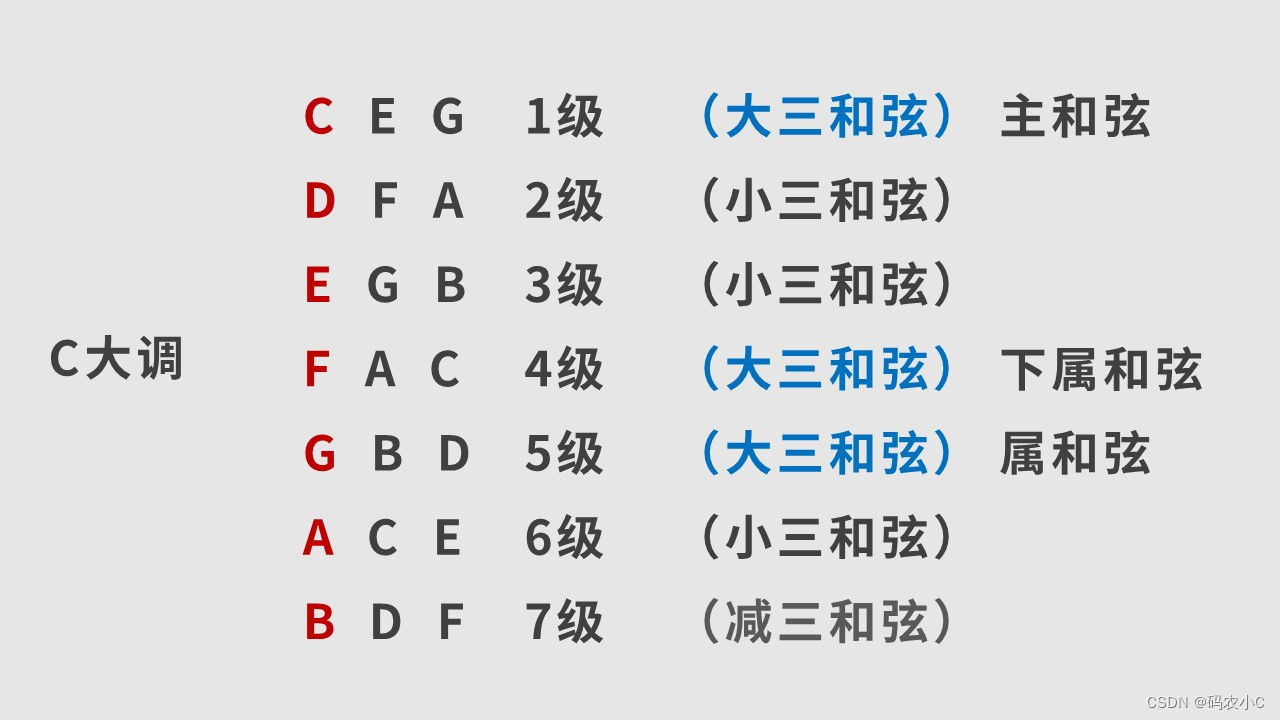
23、七和弦
24、九和弦
25、挂留和弦
26、转位和弦
29、中古调式
相关文章:

乐理-笔记
乐理笔记整理 1、前言2、认识钢琴键盘及音名3、升降号、还原号4、如何区分同一音名的不同键?5、各类音符时值的关系6、歌曲拍号7、拍号的强弱规律8、歌曲速度(BPM)9、附点音符10、三连音12、唱名与简谱数字13、自然大调(白键&…...

java八股文面试[数据库]——B树和B+树的区别
B树是一种树状数据结构,它能够存储数据、对其进行排序并允许以O(logn)的时间复杂度进行查找、顺序读取、插入和删除等操作。 1、B树的特性 B树中允许一个结点中包含多个key,可以是3个、4个、5个甚至更多,并不确定,需要看具体的实…...
2、Nginx 安装
文章目录 2、Nginx 安装2.1 官网下载2.2 安装 nginx2.2.1 第一步2.2.2 第二步2.2.3 第三步,安装 nginx2.2.4 第四步,修改防火漆规则 【尚硅谷】尚硅谷Nginx教程由浅入深 志不强者智不达;言不信者行不果。 2、Nginx 安装 2.1 官网下载 nginx…...

最适合 AI 的 Python Web 框架
迷途小书童的 Note 读完需要 4分钟 速读仅需 2 分钟 1 简介 本文将介绍 Gradio 库,它是 Python 的一个 web 框架,可以帮助我们快速构建交互式 AI 应用。我们将了解 Gradio 的应用场景、基本原理、功能介绍,并通过一个代码示例来演示如何使用 …...

算法通关村第十八关——回溯
回溯很大感觉就是多重递归,在递归的题目中,例如斐波那契数列,只需要考虑当前情况以及他的子情况。而在回溯中,要进行很多次递归,并且要对条件进行处理。 LeetCode257:给你一个二叉树的根节点root,按任意顺序ÿ…...
使用kafka还在依赖Zookeeper,kraft模式了解下
Kafka的Kraft模式 概述 Kafka是一种高吞吐量的分布式发布订阅消息系统,它可以处理消费者在网站中的所有动作流数据。其核心组件包含Producer、Broker、Consumer,以及依赖的Zookeeper集群。其中Zookeeper集群是Kafka用来负责集群元数据的管理、控制器…...
【100天精通Python】Day52:Python 数据分析_Numpy入门基础与数组操作
目录 1 NumPy 基础概述 1.1 NumPy的主要特点和功能 1.2 NumPy 安装和导入 2 Numpy 数组 2.1 创建NumPy数组 2.2 数组的形状和维度 2.3 数组的数据类型 2.4 访问和修改数组元素 3 数组操作 3.1 数组运算 3.2 数学函数 3.3 统计函数 4 数组形状操作 4.1 重塑数组形…...

Day01-Java基础语法
目录 1. 人机交互 1.1 什么是cmd? 1.2 如何打开CMD窗口? 1.3 常用CMD命令 1.4 CMD练习 1.5 环境变量 2. Java概述 1.1 Java是什么? 1.2下载和安装 1.2.1 下载 1.2.2 安装 1.2.3 JDK的安装目录介绍 1.3 HelloWorld小案例 2.3.1 …...

代码随想录二刷day06
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣242. 有效的字母异位词二、力扣349. 两个数组的交集三、力扣202. 快乐数四、力扣1两数之和 前言 一、力扣242. 有效的字母异位词 class Solution {pub…...
可扩展的Blender插件开发汇总
成熟的 Blender 3D 插件是令人惊奇的事情。作为 Python 和 Blender 的新手,我经常发现自己被社区中的人们创造的强大的东西弄得目瞪口呆。坦率地说,其中一些包看起来有点神奇,当自我怀疑或冒名顶替综合症的唠叨声音被打破时,很容易想到“如果有人能做出可以做xxx的东西就好…...
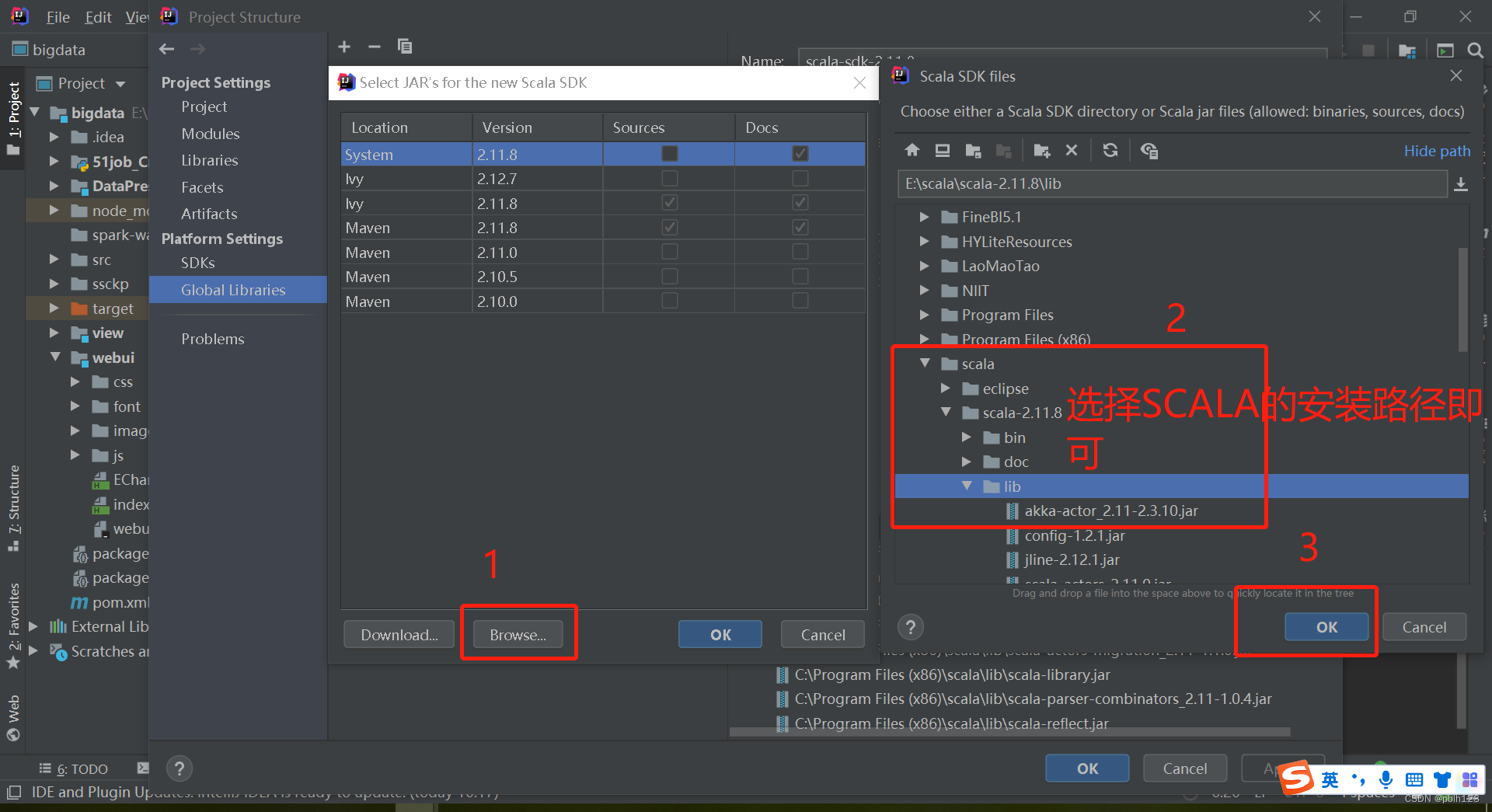
2023_Spark_实验二:IDEA安装及配置
一、下载安装包 链接:百度网盘 请输入提取码 所在文件夹:大数据必备工具--》开发工具(前端后端)--》后端 下载文件名称:ideaIU-2019.2.3.exe (喜欢新版本也可安装新版本,新旧版本会存在部分差异) IDEA …...

小赢科技,寻找金融科技核心价
如果说金融是经济的晴雨表,是通过改善供给质量以提高经济质量的切入口,那么金融科技公司,就是这一切行动的推手。上半年,社会经济活跃程度提高背后,金融科技公司既是奉献者,也是受益者。 8月29日࿰…...
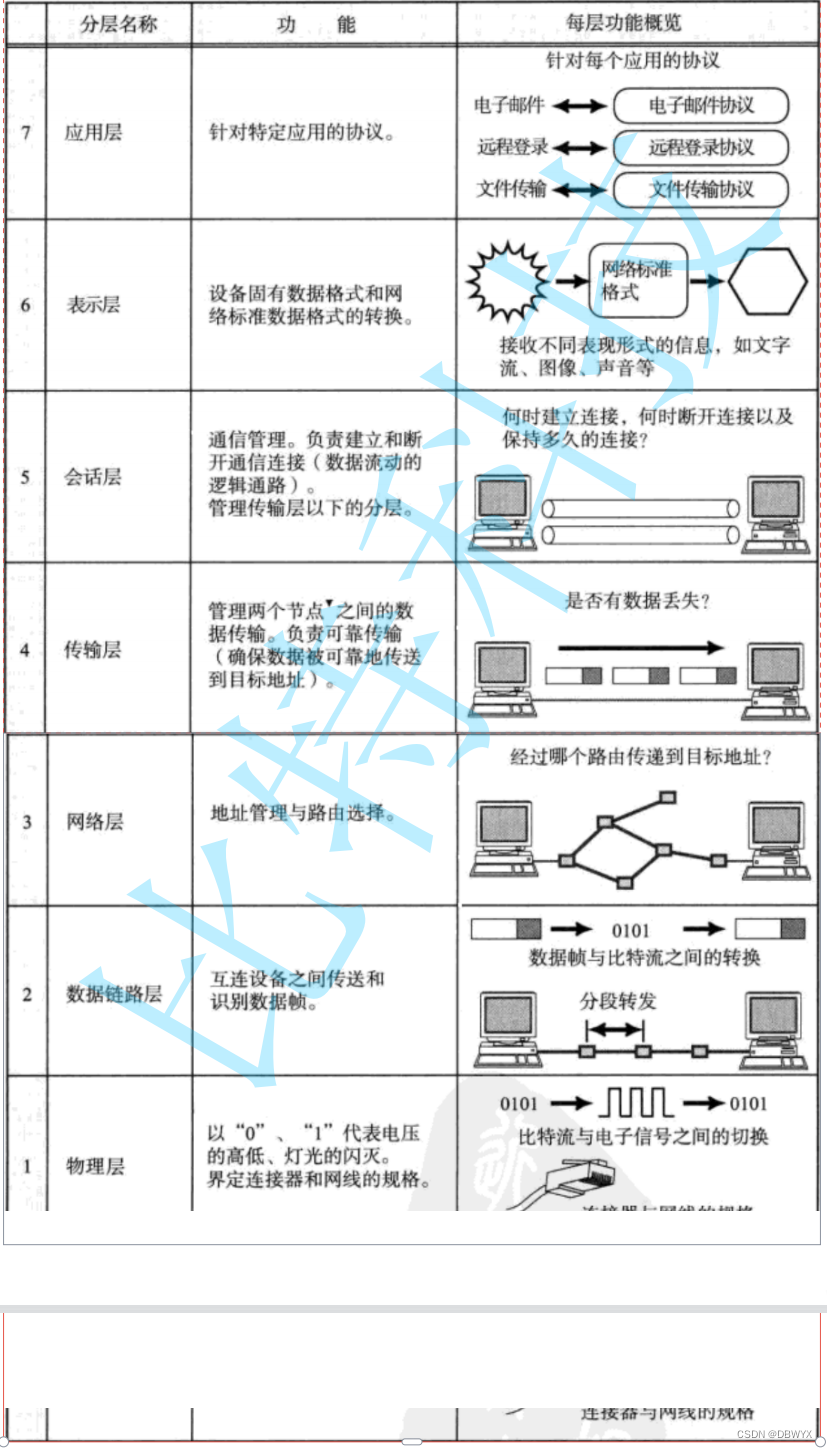
NAT与代理服务器
1.DNS Domain Name System 是一整套从域名映射到IP的系统(把域名转化为IP地址) 2.域名简介 3.周鸿祎 傅盛 4.ICMP协议 用来网络故障排查原因 草图理解“位置” ping ICMP 是绕过TCP UDP传输协议的,没有端口号 traceroute 5.NAT技术 N…...
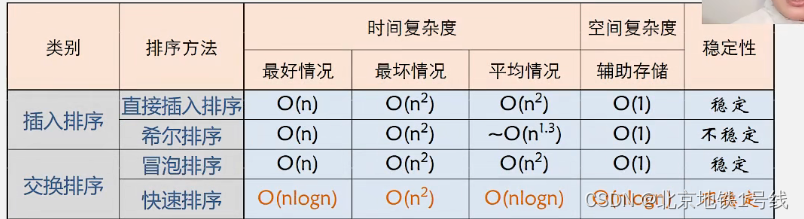
24.排序,插入排序,交换排序
目录 一. 插入排序 (1)直接插入排序 (2)折半插入排序 (3)希尔排序 二. 交换排序 (1)冒泡排序 (2)快速排序 排序:将一组杂乱无章的数据按一…...
Navicat16安装教程
注:因版权原因,本文已去除破解相关的文件和内容 1、在本站下载解压后即可获得Navicat16安装包和破解补丁,如图所示 2、双击“navicat160_premium_cs_x64.exe”程序,即可进入安装界面, 3、点击下一步 4、如图所示勾选“…...

【看表情包学Linux】初识文件描述符 | 虚拟文件系统 (VFS) 初探 | 系统传递标记位 | O_TRUNC | O_APPEND
爆笑教程《看表情包学Linux》👈 猛戳订阅! 💭 写在前面:通过上一章节的讲解,想必大家已对文件系统基本的接口有一个简单的了解,本章我们将继续深入讲解,继续学习系统传递标志位&…...
ssm+vue“魅力”繁峙宣传网站源码和论文
ssmvue“魅力”繁峙宣传网站源码和论文102 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 摘 要 随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,通过科技手段提高自身…...
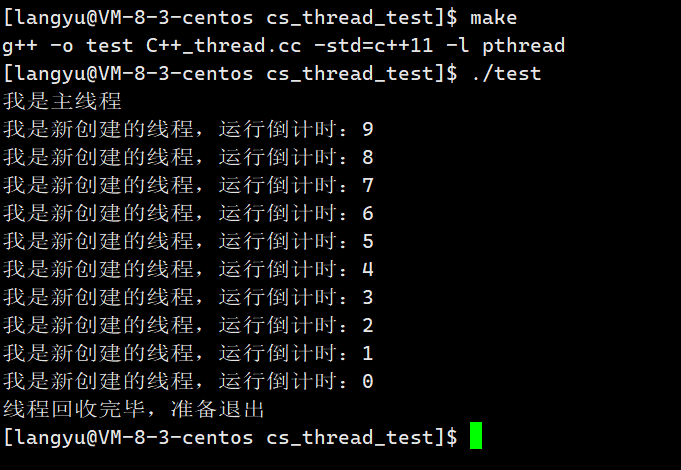
Linux系统编程5(线程概念详解)
线程同进程一样都是OS中非常重要的部分,线程的应用场景非常的广泛,试想我们使用的视频软件,在网络不是很好的情况下,通常会采取下载的方式,现在你很想立即观看,又想下载,于是你点击了下载并且在…...

leetcode645. 错误的集合(java)
错误的集合 题目描述优化空间代码演示 题目描述 难度 - 简单 LC645 - 错误的集合 集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合 丢失了一个数字 并且 有一个数…...

Pytest参数详解 — 基于命令行模式
1、--collect-only 查看在给定的配置下哪些测试用例会被执行 2、-k 使用表达式来指定希望运行的测试用例。如果测试名是唯一的或者多个测试名的前缀或者后缀相同,可以使用表达式来快速定位,例如: 命令行-k参数.png 3、-m 标记࿰…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
