刷完这19道leetcode二分查找算法,不信进不了大厂
对于二分题,其实就是设定一个中间值 mid, 然后通过这个值进行一个判断 check(mid), 通过这个函数的返回值,判断将不可能的一半剪切掉;
在刷题的时候需要注意主要是两部分,check 函数的定义以及边界的选择(等号的选择,以及最后是 return left 还是 right)
这次主要是 LC 的二分专题,里面的简单题基本都是比较显性的提示了 check 函数的构建,比方说直接找出某个值,而难题一般都是 check 函数比较难想的,这个时候就需要经验了;
广义上只要是排好序(局部排序),只要是找某个值,大部分都可以考虑用二分,这样复杂度可以降低很多;
对于边界,我的循环结束条件是 left <= right , 因为如果要多记很多模板,怕会出问题,所以退出条件基本都按这个,然后无论是那种模块,都基于这个结束条件来判断,这样可以把问题收缩都循环里的判定的 check 函数,多做了就会发现端倪;
然后关于退出之后 left 还是 right ,这个是具体问题具体分析;由于我的结束判定条件是 left<=right ,所以如果没用中间返回,那么必然存在 left === right 的时候,这个时候根据判定条件,就知道 right 在 left 的前面,而到底是左逼近,还是右逼近,都比较好判断了,因为这个时候已经退出去了,left 和 right 所代表的 check 的状态也是显而易见的,那么看题目要求什么,给什么即可;
对于二分,我觉得这个专题就基本足够了,简单居多,难题也有两个;如果是第一次学习二分,那么按照专栏的三个模板去记忆也 ok, 别人的经验终归是适合别人自己,做题最重要是把握住自己的节奏,记忆自己最熟悉的那个点,强行模仿别人反而落了下乘;
当然那个男人那么强,我的做题就是模仿的他,慢慢大佬的解法就是我自己的节奏了,毕竟模仿多了,其实就是自己的了,除了算法,其他的工程化学习也是一样的;
那么,周末快乐,下周开 dp 吧,毕竟这个听有意思的。
模板 1
- 目标值是一个固定的 target,在二分过程中需要不断的判断,如果成功就返回对应的值,否则直接返回失败的值
- 返回值如果是向下取,返回 right,如果向上取,则返回 left,还有可能返回一个特定给的失败值;
var search = function (fn, target) {let left = 最小值,right = 最大值;while (left <= right) {// 取 mid 值const mid = ((right - left) >> 1) + left;//这里的 fn 可能是函数,也可能只是数组取值,反正就是可以取得一个值去跟 target 比较const temp = fn(mid);if (temp === target) return mid;if (temp < target) {left = mid + 1;} else {right = mid - 1;}}return 没有精确匹配后的值;
};704. 二分查找
var search = function (nums, target) {const len = nums.length;if (!len) return -1;let left = 0,right = len - 1;while (left <= right) {const mid = ((right - left) >> 1) + left;if (nums[mid] === target) return mid;if (nums[mid] < target) {left = mid + 1;} else {right = mid - 1;}}return -1;
};69. x 的平方根
// 69. x 的平方根
var mySqrt = function (x) {let left = 0,right = x;while (left <= right) {const mid = ((right - left) >> 1) + left;const sqrt = mid * mid;if (sqrt === x) return mid;if (sqrt < x) {left = mid + 1;} else {right = mid - 1;}}// 向下取整return right;
};374. 猜数字大小
分析
- 这里内置一个函数 guess(n), 返回值是 -1 0 1, -1 是 targt 值更小
var guessNumber = function (n) {let left = 1,right = n;while (left <= right) {const mid = ((right - left) >> 1) + left;if (guess(mid) === 0) return mid;if (guess(mid) > 0) {// 这个时候 mid < pickleft = mid + 1;} else {right = mid - 1;}}
};// 自己模拟一下这个 guess 函数吧 -- 假定第二个参数就是目标猜的数字,我们可以用它来初始化,默认是5
function guess(num, pick = 5) {if (num === pick) return 0;if (pick < num) return -1;if (pick > num) return 1;
}参考视频:传送门
441. 排列硬币
分析
- 这里求的是一个左侧极值的二分法,是向右逼近的二分
- 累计值算法是小学数学题 sum = (first+end)*count/2
- 每次取中间层数,求出到这个层数需要的币数 sum,然后和目标值 n 比较
- 如果刚好符合,直接返回(这里可以收缩到左侧判定条件中);如果 count 比较少,则 left 要提到 mid+1,否则 right 要提到 mid-1
- 由于最后要返回的是最逼近 n 的层数,所以判断一下当 left === right 情况,如果小于 n,则 left = mid+1,这个时候 right 符合要求,所以跳出循环后,返回的是 right
- 时间复杂度O(logN)
var arrangeCoins = function (n) {let left = 0,right = n;while (left <= right) {const mid = left + ((right - left) >> 1);// mid 层的时候满的硬币数const sum = ((1 + mid) * mid) / 2;if (sum === n) return mid;if (sum < n) {left = mid + 1;} else {right = mid - 1;}}return right;
};33. 搜索旋转排序数组
分析
- 已知:原始数组 nums 是生序排序的,且数组中的值不一样的
- 入参的 nums 是在某个下标 k 的作用下发生了重置,使得 nums 现在是先升序数组 [k,len-1]然后断裂后,再一个升序数组[0,k-1]
- 这是一个局部排好序的数组,所以可以用二分处理,返回的是 target 值的下标或者 -1
- 所以每次都用排好序的一半来作为判断依据,如果在排好序这边,则删除另外,反之亦然
- 时间复杂度 O(logn)
var search = function (nums, target) {let left = 0,right = nums.length - 1;while (left <= right) {const mid = ((right - left) >> 1) + left;if (nums[mid] === target) return mid;if (nums[mid] >= nums[left]) {// [left,mid] 是有序的if (nums[left] <= target && target < nums[mid]) {// target 在[left , mid) 中right = mid - 1;} else {left = mid + 1;}} else {// [mid,right] 是有序的if (nums[mid] < target && target <= nums[right]) {// target 在(mid , right] 中left = mid + 1;} else {right = mid - 1;}}}return -1;
};模板 2 – 需要用到邻居值判断
相比于模板 1,模板 2 中不是仅有一个符合条件值,而是一系列值,我们需要找到符合要求的那个 极值,比方说是符合条件的最大值/第一个值 等;
var search = function (fn) {let left = 最小值,right = 最大值;while (left <= right) {// 取 mid 值const mid = ((right - left) >> 1) + left;//这里的 fn 可能是函数,也可能只是数组取值,反正就是可以取得一个值去跟 target 比较const bool = fn(mid);if (bool) {// 成功了,要向还没成功的地方寻找right = mid - 1;} else {left = mid + 1;}}return 特定的值;
};278. 第一个错误的版本
分析
- 这里要找出的是第一个错误版本,而整理版本排列是
正常 -> 错误,所以这里是根据错误向左逼近 - 如果是错误版本, right 指针不断往左,如果是正常版本,left 指针不断往右,当左右指针相交时,如果是错误版本,right 继续往左,到达正常区,这个时候 left 就是第一个错误版本了
- 时间复杂度 O(logn)
var solution = function (isBadVersion) {return function (n) {let left = 1,right = n;while (left <= right) {const mid = ((right - left) >> 1) + left;if (isBadVersion(mid)) {// 如果是错误版本right = mid - 1;} else {left = mid + 1;}}return left;};
};162. 寻找峰值
分析
- 已知多峰的时候只需返回一个即可,那么就是直接做二分判断即可;
- 两侧边缘值也可以是峰值,因为题目给了两侧是 -Infinity;
- 犹豫已经存在整体区域外的最低点,所以只要找到一个局部下降区域,那么局部上升区域中肯定存在峰值;
var findPeakElement = function (nums) {nums[-1] = nums[nums.length] = -Infinity; // 设置边界值,这样保证在边缘的时候也只需要两个值就能判极值let left = 0,right = nums.length - 1;while (left <= right) {const mid = ((right - left) >> 1) + left;// 找出一个有峰值的区间if (nums[mid] > nums[mid + 1]) {// [mid,right] 局部下降,而[-1,mid] 是局部上升的,比较有一个最低值right = mid - 1;} else {left = mid + 1;}}return left;
};153. 寻找旋转排序数组中的最小值
分析
-
这里其实就是找谷值,注意的是,这里的值互不相等且局部单增 ,所以可以加一个辅助条件 nums[-1] = nums[len] = infinite,这样能保证谷值在边缘也能直接找到
-
注意:这里返回的是最小值,而不是最小坐标
-
注意取得 mid 值之后,将 mid 与 right 的值比较,只会出现两种情况,
- 如果 nums[mid]<=nums[right] ,则 mid 和 right 重合或 mid 在 right 之后且单增,这个时候无论是在第一个单增区间还是第二个,谷点都在 mid 之钱,所以 right = mid-1
var findMin = function (nums) {let len = nums.length;nums[-1] = nums[len] = Infinity;let left = 0,right = len - 1;while (left <= right) {const mid = ((right - left) >> 1) + left;if (nums[mid - 1] > nums[mid] && nums[mid] < nums[mid + 1])return nums[mid]; //谷值if(nums[mid]<=nums[right]){// [mid,right] 单增// 注意这个等号为啥要加,可以考虑一下如果 left 和 right 相等时,对应的 mid 也是这个点,那么是让 right 走,还是让 left 走;这里我们最后返回值是 left,所以让 right 走一步结束战斗right = mid-1}else{left = mid+1}}return nums[left];
};154. 寻找旋转排序数组中的最小值 II
- 和 153. 寻找旋转排序数组中的最小值 类似,但是由于值可以重复,无法直接判断单增区间
- 所以想办法将右侧与 mid 相等的值先删除掉,这个时候剩下的不同值可以与 153 题一样做处理了
var findMin = function(nums) {const len = nums.lengthnums[-1] = nums[len] = Infinitylet left = 0,right = len-1while(left<=right){const mid = ((right-left)>>1) + left// 将右侧与 mid 同值的值删掉while(nums[right] === nums[mid] && right>mid){right -- }// 由于存在重复值,所以拐点值右侧可以是直线,而不一定是单增if(nums[mid-1]>nums[mid] && nums[mid]<=nums[mid+1]) return nums[mid]if(nums[mid]<=nums[right]){// 上一题这里的等号是当 left 和 right 重合时的特殊情况// 现在由于值可能重复,所以不能直接判断出 [mid,right] 是递增的区间了,所以要先为右侧相同的值进行删减,然后再进行即可right = mid-1}else{left = mid+1}}return nums[left]
};模板3
在排序数组中查找元素的第一个和最后一个位置
分析
- 正常查找 target 值,直到找到左侧第一个,
- 如果没有找到,则直接返回 [-1,-1]
- 如果找到了左侧的 target 值,这个时候以左侧 left 为起点,再进行一次二分,求右侧第一个 target 值,最后返回即可
- 时间复杂度 O(logn)
var searchRange = function(nums, target) {if(!nums) return [-1,-1]let left = 0,right = nums.length-1let ret = []// 找左节点while(left<=right){const mid = ((right-left)>>1) + leftif(nums[mid]<target){left = mid+1}else{right = mid-1}}if(nums[left]!== target) return [-1,-1]// 找右节点let l = left,r = nums.length-1while(l<=r){const mid = ((r-l)>>1) + lif(nums[mid]>target){r = mid-1}else{l = mid+1}}return [left,r]
};658. 找到 K 个最接近的元素
分析
- 先找出 arr 中值最靠近 x 左侧的下标值 – 如果有等于 x 的就取 x 没有就取最靠近的前一个
- 然后开始向两边扩散找接近 x 的前 k 个值
- 时间复杂度 O(log(n))
var findClosestElements = function (arr, k, x) {let l = 0,r = arr.length - 1;while (l <= r) {const mid = ((r - l) >> 1) + l;if (arr[mid] > x) {r = mid - 1;} else {l = mid + 1;}}// 这个时候 r 是左侧最靠近 x 的值下标,l 是右侧最靠近 x 的值let lIndex = r,rIndex = l; // 防止混淆let ret = [];while (k--) {let isLeft = true;if (lIndex >= 0 && rIndex < arr.length) {isLeft = x - arr[lIndex] <= arr[rIndex] - x;} else if (rIndex < arr.length) {isLeft = false;}if (isLeft) {ret.unshift(arr[lIndex]);lIndex--;} else {ret.push(arr[rIndex]);rIndex++;}}return ret;
};其他练习题
50. Pow(x, n)
分析
- 直接将 n 进行拆分,然后递归求值 – 然后超时了,因为很多值都是重复的,
- 然后就是快速迭代我们 2 - 4 -16
- 值得注意的是,这里 n 的取值是 [-231,231-1] 本来没啥事,但是吧,你将 n 转成正数再执行, 那么 n >> 1 就有事了,一旦 n 是 -2^31,那么第一次递归的时候 recursion 的 n 就是负数了
- 所以要用 >>> 或者用数学的方法
- 时间复杂度 O(logn)
var myPow = function (x, n) {const recursion = (n) => {if (n === 0) return 1;// const y = recursion(n >> 1);const y = recursion(Math.floor(n / 2));return n % 2 ? y * y * x : y * y;};return n < 0 ? 1 / recursion(-n) : recursion(n);
};console.log(myPow(2.1, 3));
console.log(myPow(2, -2));367. 有效的完全平方数
/** * @分析 * 1. 概念:若 x*x = y , 则 y 是完全平方数 */
var isPerfectSquare = function (num) {let left = 0,right = num;while (left <= right) {const mid = ((right - left) >> 1) + left;const temp = mid * mid;if (temp === num) return true;if (temp > num) {right = mid - 1;} else {left = mid + 1;}}return false;
};744. 寻找比目标字母大的最小字母
分析:
- 注意: 这道题应该改成,给定一个排好序的字符数组,找出处 target 所在位置的下一个字母,且该数组首尾衔接 – 即如果给定的 target 在数组最后,则下一个就是首字母;
- 字母先转成 UniCode 编码,然后用 编码大小来进行比较,注意这里只有小写字母,所以 left right 值也是有了
- 这是个奇葩的设定,[‘a’,‘c’],‘z’ , 如果按照真正 charCode 比较,数组中没有比 ‘z’ 大的,这里这能说是顺序遍历数组后,在 target 之后的第一个元素
- 时间复杂度: O(logN)
var nextGreatestLetter = function(letters, target) {const targetIndex = target.charCodeAt()let left = 0,right = numbers.length-1while(left <= right){const mid = ((right-left) >> 1) + leftif(letters[mid].charCodeAt()>targetIndex){// 只要是符合的,都返回往左走,知道走不了right = mid-1}else{left= mid+1}}if(left>=numbers.length) return letters[0]return letters[left]};349. 两个数组的交集
分析:
- 先为 nums1 和 nums2 排序,然后遍历其中一个数组,另外一个数组做二分查找,最后得到结果
- 这里直接取nums1 做遍历,实际可以找个长度少的遍历,长度大的做二分,这样查找过程的时间复杂度即为 O(nlogm), 其中 n<=m
- 但是由于做了排序,实际的时间复杂度是 mlogm m 是大的那个长度
var intersection = function (nums1, nums2) {const l1 = nums1.length,l2 = nums2.length;if (!l1 || !l2) return [];// 先排序nums1.sort((a, b) => a - b);nums2.sort((a, b) => a - b);const ret = [];for (let i = 0;i<l1;i++) {if(i>0 && nums1[i-1] === nums1[i]) continue // 重复值跳过const n = nums1[i];let left = 0,right = l2-1;while (left <= right) {const mid = ((right - left) >> 1) + left;if (nums2[mid] === n) {ret.push(n);break;}if (nums2[mid] > n) {right = mid - 1;} else {left = mid + 1;}}}return ret
};350. 两个数组的交集 II
- 直接用 map 将其中一个数组的值映射保存起来
- 然后遍历另外的数组,每一次匹配成功,则map 的值减一,ret 数组 push 上这个值
- 直到 map 中的这个值为 0,则这个值在两个数组中的最大公约数达到,不再进行 push 咯
- 时间复杂度 O(n+m) , 空间复杂度 O(n) 其中 n 可以是小的那个数组的不同值长度
var intersect = function (nums1, nums2) {const map = new Map(); //将长数组的值存储一份for (let item of nums2) {if (map.has(item)) {map.set(item, map.get(item) + 1);} else {map.set(item, 1);}}let ret = [];for(let item of nums1){if(!!map.get(item)){map.set(item,map.get(item)-1)ret.push(item)}}return ret;
};167. 两数之和 II - 输入有序数组
分析
- numbers 是升序数组,找出 n1+n2 = target , 返回 n1,n2 对应的下标值 [i1,i2] – 注意下标值从 1 开始
- 每个输入只有唯一的输出值
- 时间复杂度 nlogn
var twoSum = function (numbers, target) {for (let i = 0; i < numbers.length-1; i++) {const temp = target - numbers[i];let l = i + 1,r = numbers.length - 1;while (l <= r) {const mid = ((r - l) >> 1) + l;if (numbers[mid] === temp) return [i + 1, mid + 1];if (numbers[mid] < temp) {left = mid + 1;} else {right = mid - 1;}}}
};287. 寻找重复数
分析
- 给定长度为 n+1 的 nums,里面的值都是 1-n, 本题中只有一个值是重复的,找出这个值
- 注意这里只是表明重复的只有一个值,但是这个值重复多少次并没有说明,所以不能用简单的异或二进制处理
- 但是我们可以选定以 mid 值,然后判断小于等于 mid 值 count,如果 count 超出了 mid ,证明在 [1,mid] 中至少有一个值重复了,这个时候可以砍掉右侧部分
- 当 left 和 right 相等之后,即找到了唯一重复的值,因为这个时候左右两侧的值都不服要求,就只有这个了
- 时间复杂度 O(nlohn), 空间复杂度 1
var findDuplicate = function (nums) {let left = 1,right = nums.length - 1; // 值是 1 - nwhile (left < right) {const mid = ((right - left) >> 1) + left;const count = nums.reduce((prev, cur) => (cur <= mid ? prev + 1 : prev), 0); // 小于等于 count 的值if (count > mid) {// 如果 [1,mid] 这个数组满值的情况才只有 mid 个,现在 count 如果比这个还大,证明重复的值在这里面right = mid;} else {left = mid + 1;}}return left;
};4.寻找两个正序数组的中位数
分析
- 已知两个有序数据,求中位数 (和求第 k 小没啥区别)
- 根据两个数组的大小,将题转成求第 k 小的题目
- 这题使用二分没能直接过,判定条件边界很多,最后放弃直接用二分处理掉了
var findMedianSortedArrays = function (nums1, nums2) {const n = nums1.length,m = nums2.length;let sum = n + m; // 如果是偶数,取两个值 prev,cur ,取中间值let k = (sum + 1) / 2; // 可以是非整数let cur;while (k >= 1) {if (!nums1.length) {cur = nums2.shift();} else if (!nums2.length) {cur = nums1.shift();} else {if (nums1[0] <= nums2[0]) {cur = nums1.shift();} else {cur = nums2.shift();}}k--;}let next;if (k !== 0) {// 这里用 ?? 而不是用 || , 是因为判断 nums[0] 是否为 undefined,而如果是 0 的时候,取 0 而非切换到 Infinity;next = Math.min(nums1[0] ?? Infinity, nums2[0] ?? Infinity);return (cur + next) / 2;}return cur;
};410. 分割数组的最大值
分析
- 切分数组 nums,使得切割后数组和最大的那个值最小 – 子数组是连续的;
- 也就是尽可能按照总和均匀的将值分配到每一个数组中,且每个数组中最少有一个值,所以最小值应该就是 max(nums[i]), 最大值是 sum(nums)
- 设计一个函数 check(max), 判断是否能切割出 m 个连续子数组,且值小于等于 max;如果可以,证明这个是一个较大值,可以继续向左侧逼近,找到一个更小的值;如果不可以,证明这个值 max 偏小了,需要求的值在右侧.
- 这里最需要注意的是,切割的子组件是连续的;同时每一个数组至少有一个值;
- 只要捋清楚 check 这个函数,基本就能每次都切掉一半,直接拿到最后值了;
var splitArray = function (nums, m) {// 先找到 left 和 rightlet left = 0,right = 0;for (let num of nums) {left = Math.max(num, left);right += num;}// 切割最大值不超过 max 的数组,如果切出来的数组数量少于 m,则证明可以切得更新,发挥 true// 如果切除来的数组数量超出了 m, 证明只且 m 组的时候,最小值要超出 max 了,返回 falsefunction check(max) {let ret = 0,sum = 0;let i = 0;while (i < nums.length) {sum += nums[i];if (sum >max) {// 一旦超出 max,则分组结束,sum 重新设置为 nums[i]ret++;sum = nums[i];}i++}// 如果最后还有剩,单独成团ret = sum ? ret + 1 : ret;return ret<=m}while (left <= right) {const mid = ((right - left) >> 1) + left;if (check(mid)) {// 如果能找到,向左逼近 -- right 最后得到的是一个不成功的值,因为只要成功它就要发生改变right = mid - 1;} else {// left 最终出去的时候,肯定代表一个成功的值left = mid + 1;}}return left;};相关文章:

刷完这19道leetcode二分查找算法,不信进不了大厂
对于二分题,其实就是设定一个中间值 mid, 然后通过这个值进行一个判断 check(mid), 通过这个函数的返回值,判断将不可能的一半剪切掉; 在刷题的时候需要注意主要是两部分,check 函数的定义以及边界的选择(…...

四、Plugin Request and Sometimes pads
Request and Sometimes pads 到目前为止,我们只处理了总是可用的pad。然而,也有一些pad仅在某些情况下创建,或者仅在应用程序请求pad时创建。第一个有时被称为a;第二个被称为请求pad。pad的可用性(always, sometimes or request)可以在pad的…...

唤醒手腕 Java 后端 Springboot 结合 Redis 数据库学习笔记(更新中)
Redis 基本介绍 Redis Introduction The open source, in-memory data store used by millions of developers as a database, cache, streaming engine, and message broker. 基本概念:redis 是一个开源的、使用 C 语言编写的、支持网络交互的、可基于内存也可持…...
robotiq 2f 140安装在UR3机械臂后面在gazebo仿真中散架、抖动
robotiq 2f 140安装在UR3机械臂后面在gazebo仿真中散架、抖动 搭建环境: ubuntu: 20.04 ros: Nonetic sensor: robotiq_ft300 gripper: robotiq_2f_140_gripper UR: UR3 通过上一篇博客配置好ur3、力传感器和robotiq夹爪的gazebo仿真环境后,夹爪看起来…...

坐标系概念 四元数 欧拉角
1、四个概念:“地理”坐标系、“机体”坐标系、他们之间换算公式、换算公式用的系数。地理坐标系:东、北、天,以下简称地理。在这个坐标系里有重力永远是(0,0,1g),地磁永远是(0,1,x)…...

从0开始写Vue项目-SpringBoot整合Mybatis-plus实现登录、注册功能
1.从0开始写Vue项目-环境和项目搭建_慕言要努力的博客-CSDN博客 2. 从0开始写Vue项目-Vue2集成Element-ui和后台主体框架搭建_慕言要努力的博客-CSDN博客 3. 从0开始写Vue项目-Vue页面主体布局和登录、注册页面_慕言要努力的博客-CSDN博客 一、前言 在之前我们以及搭建好了基…...
K8s中gRpc通信负载均衡失效
上篇文章在做 整合K8sSpringCloudK8sSpringBootgRpc 时,发现K8s中使用gRpc通信,负载均衡功能失效查了下gRpc的最佳实践,找到这里Load balancingSome load balancers dont work effectively with gRPC. L4 (transport) load balancers operate…...

第三届区块链服务网络(BSN)全球合作伙伴大会在杭州成功举办
为持续推动分布式技术和产业创新发展,2023年2月17日,由杭州市人民政府指导,杭州市拱墅区人民政府、国家信息中心主办,中国移动通信集团有限公司、区块链服务网络(BSN)发展联盟承办,中国移动通信…...
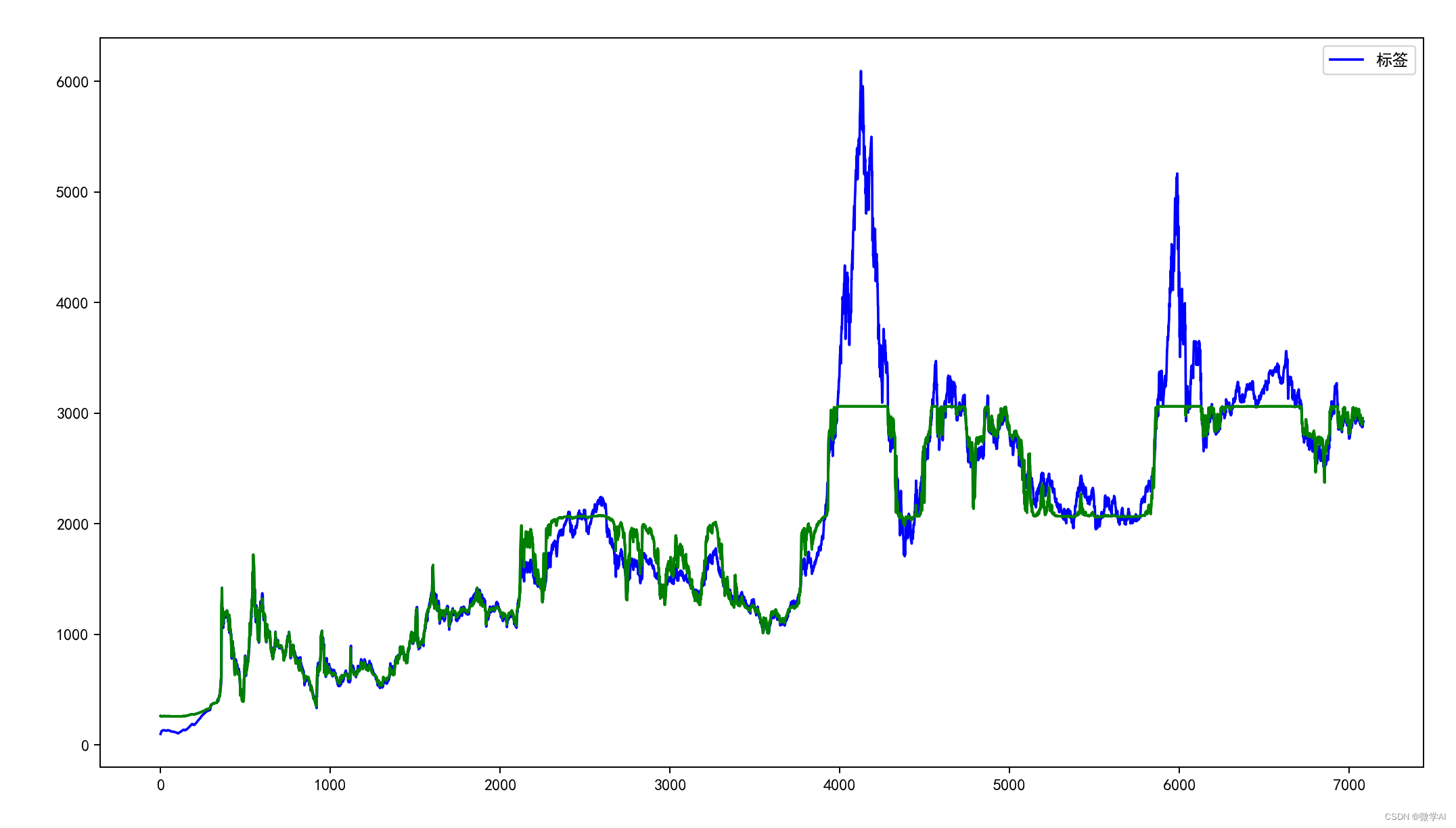
人工智能基础部分13-LSTM网络:预测上证指数走势
大家好,我是微学AI,今天给大家介绍一下LSTM网络,主要运用于解决序列问题。 一、LSTM网络简单介绍 LSTM又称为:长短期记忆网络,它是一种特殊的 RNN。LSTM网络主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题…...

内网穿透/组网/设备上云平台EasyNTS上云网关的安装操作指南
EasyNTS上云网关的主要作用是解决异地视频共享/组网/上云的需求,网页对域名进行添加映射时,添加成功后会生成一个外网访问地址,在浏览器中输入外网访问地址,即可查看内网应用。无需开放端口,EasyNTS上云网关平台会向Ea…...
易点天下基于 StarRocks 全面构建实时离线一体的湖仓方案
作者:易点天下数据平台团队易点天下是一家技术驱动发展的企业国际化智能营销服务公司,致力于为客户提供全球营销推广服务,通过效果营销、品牌塑造、垂直行业解决方案等一体化服务,帮助企业在全球范围内高效地获取用户、提升品牌知…...
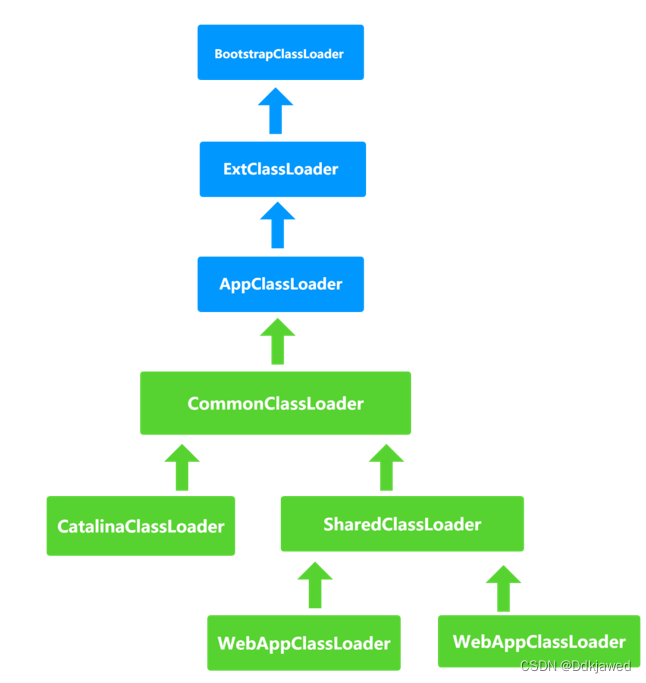
Tomcat的类加载机制
不遵循双亲委托 在JVM中并不是一次性地把所有的文件都加载到,而是按需加载,加载机制采用 双亲委托原则,如下图所示: BootStrapClassLoader 引导类加载器ExtClassLoader 扩展类加载器AppClassLoader 应用类加载器CustomClassLoad…...

【shell 编程大全】数组,逻辑判断以及循环
数组,逻辑判断以及循环1. 概述 大家好,我又来了。今天呢我们继续学习shell相关的知识。还是老样子我们先回顾下上一次【脚本交互 以及表达式】学习到的知识 登录shell 关联配置文件什么是子shellumask 修改默认权限read 基础表达式 简单计算表达式expr 计…...

Android13 Bluetooth更新
目录 Android 13 版本说明 LE Audio 代码更新 Android 12代码路径 Android 13代码路径 Android 13 版本说明 里面对蓝牙更新的描述较少,一出提到蓝牙的一...
手工测试混了5年,年底接到了被裁员的消息....
大家都比较看好软件测试行业,只是因为表面上看起来:钱多事少加班少。其实这个都是针对个人运气好的童人才会有此待遇。在不同的阶段做好不同阶段的事情,才有可能离这个目标更近,作为一枚软件测试人员,也许下面才是我们…...
Umi框架
什么是 umi umi 是由 dva 的开发者 云谦 编写的一个新的 React 开发框架。umi 既是一个框架也是一个工具,可以将它简单的理解为一个专注性能的类 next.js 前端框架,并通过约定、自动生成和解析代码等方式来辅助开发,减少开发者的代码量。 u…...
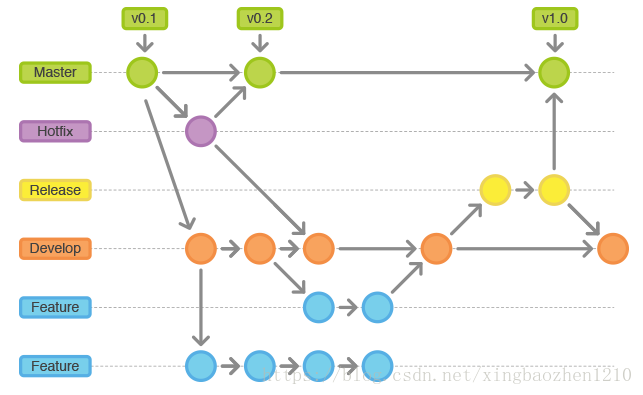
教你学git
前言 git是一种用于多人合作写项目。详细说明如下 文章目录前言什么是版本控制?什么是 Git?它就属于人工版本控制器版本控制工具常见版本控制工具怎么工作的?git 文件生命周期状态区域安装配置-- global检查配置创建仓库工作流与基本操作查看…...
【工作笔记】syslog,kern.log大量写入invalid cookie错误信息问题
任务描述 错误出现出现过四五次,应该是诊断单元tf卡读写出问题导致下面这条告警一直高频写入到/var/log/下的syslog、kern.log、messages中 Nov 23 06:25:12 embest kernel: omap_hsmmc 48060000.mmc: [omap_hsmmc_pre_dma_transfer] invalid cookie: data->hos…...

【C++】多线程
多任务处理有两种形式,即:多进程和多线程。 基于进程的多任务处理是程序的并发执行。基于线程的多任务处理是同一程序的片段的并发执行 文章目录1. 多线程介绍2. Windows多线程1. 多线程介绍 每一个进程(可执行程序)都有一个主线…...
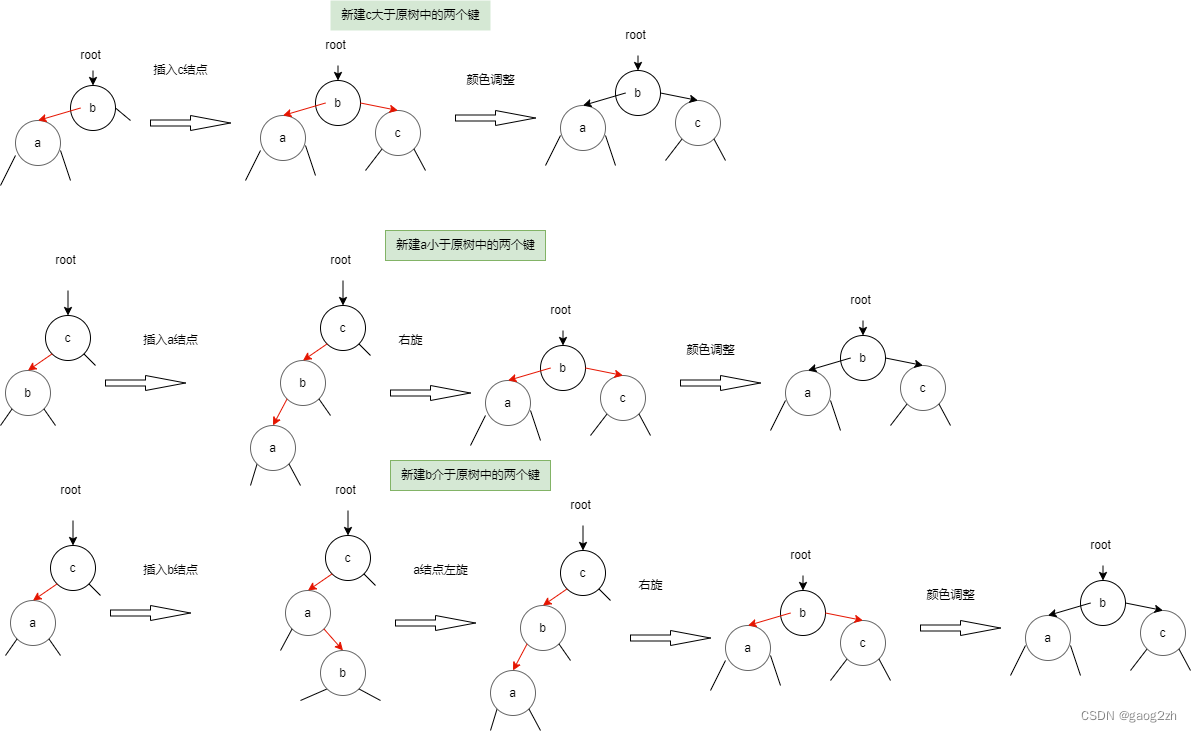
0202插入删除-算法第四版红黑树-红黑树-数据结构和算法(Java)
文章目录4 插入4.1 序4.2 向单个2-结点插入新键4.3 向树底部的2-结点插入新键4.4 向一棵双键树(3-结点)中插入新键4.5 颜色调整4.6 根结点总是黑色4.7 向树底部的3-结点插入新键4.8 将红链接在树中向上传递4.9 实现5 删除5.1 删除最小键5.2 删除6 有序性…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...
深入理解 C++ 左值右值、std::move 与函数重载中的参数传递
在 C 编程中,左值和右值的概念以及std::move的使用,常常让开发者感到困惑。特别是在函数重载场景下,如何合理利用这些特性来优化代码性能、确保语义正确,更是一个值得深入探讨的话题。 在开始之前,先提出几个问题&…...
