networkX-03-连通度、全局网络效率、局部网络效率、聚类系数计算
文章目录
- 1.连通度
- 1.1 检查图是否连通
- 1.2 检查有向图是否为强连通
- 1.3 点连通度、边连通度:
- 2.网络效率
- 2.1全局效率
- 2.2 局部效率
- 2.2.1 查找子图
- 2.2.3 局部效率源码分析
- 3.聚类系数(Clustering Coefficient)
- 3.1 聚类系统源码分析
教程仓库地址:github networkx_tutorial
本文从指标公式出发,计算网络的连通度、全局效率、局部效率、聚类系数,有需要的同学可在仓库下载ipynb文件进行练习.
1.连通度
- 文字部分来自GPT-4

import networkx as nx
import matplotlib. pyplot as plt
# 创建一个无向图
G = nx.Graph()
# 添加边
G.add_edges_from([(0, 1), (1, 2), (2, 3), (3, 4), (4, 0), (0, 2)])
# # 绘制图形
nx.draw(G,node_size=500,with_labels=True)

1.1 检查图是否连通
# 检查图是否连通
is_connected = nx.is_connected(G)
print(f"The graph is connected: {is_connected}")
The graph is connected: True
1.2 检查有向图是否为强连通
# 创建一个有向图
DG = nx.DiGraph()
DG.add_edges_from([(0, 1), (1, 2), (2, 3), (3, 4), (4, 0), (0, 2)])
nx.draw(DG,node_size=500,with_labels=True)

# 检查图是否强连通
is_strongly_connected = nx.is_strongly_connected(DG)
print(f"The directed graph is strongly connected: {is_strongly_connected}")
The directed graph is strongly connected: True
1.3 点连通度、边连通度:

# 计算点连通度
node_connectivity = nx.node_connectivity(G)
print("节点连通度:", node_connectivity)
# 计算边连通度
edge_connectivity = nx.edge_connectivity(G)
print("边连通度:", edge_connectivity)
节点连通度: 2
边连通度: 2
2.网络效率

2.1全局效率

# 创建一个简单的无向图
G = nx.Graph()
G.add_nodes_from([1, 2, 3, 4])
G.add_edges_from([(1, 2), (1, 3), (2, 3), (3, 4)])# 绘制图形
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_color='lightblue', node_size=500, font_size=16, font_weight='bold')
labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels, font_size=12, font_color='red')
plt.show()

#计算指定节点对之间的效率:节点之间最短路径的倒数
nx.efficiency(G,2,4) # 2,4 之间的最短路径长度为2,则两节点之间的效率为1/2
0.5
# 全局网络效率官方函数
nx.global_efficiency(G)
0.8333333333333334
# 源码
def global_effi(G):n = len(G)denom = n * (n - 1)if denom != 0:lengths = nx.all_pairs_dijkstra_path_length(G)g_eff = 0for source, targets in lengths:for target, distance in targets.items():if distance > 0:g_eff += 1 / distanceg_eff /= denom# g_eff = sum(1 / d for s, tgts in lengths# for t, d in tgts.items() if d > 0) / denomelse:g_eff = 0# path lengths in parallel.return g_effglobal_effi(G=G)
0.8333333333333334
2.2 局部效率
2.2.1 查找子图

# 定义要查找的节点子集
node_subset = [1, 2, 3]
# 查找诱导子图
induced_subgraph = G.subgraph(node_subset)
nx.draw(induced_subgraph,with_labels = True)

# 查找生成子图
spanning_subgraph = G.subgraph(G.nodes())
nx.draw(spanning_subgraph,with_labels = True)

2.2.3 局部效率源码分析
nx.local_efficiency(G)
0.5833333333333334
# 源码
sum = 0 # 初始化 ,所有节点和其构成的子图 ,对应的全局效率的值
len(G) # G的节点数for v in G: # 遍历每个节点print('---{}节点的子图是----'.format(v))# 找到每个节点的和其邻居构成的子图# fig,ax = plt.subplots()# nx.draw(G.subgraph(G[v]),with_labels = True,ax=ax)g_effi = nx.global_efficiency(G.subgraph(G[v]))print('邻居节点{}全局效率为:{}'.format(v,g_effi))sum = sum+ g_effiprint("local_efficiency",sum/len(G)) #0.9166666666666667---1节点的子图是----
邻居节点1全局效率为:1.0
---2节点的子图是----
邻居节点2全局效率为:1.0
---3节点的子图是----
邻居节点3全局效率为:0.3333333333333333
---4节点的子图是----
邻居节点4全局效率为:0
local_efficiency 0.5833333333333334
3.聚类系数(Clustering Coefficient)


3.1 聚类系统源码分析
# 官方函数
for node in G.nodes():c = nx.clustering(G = G,nodes=node)print(f"节点 {node} 的聚类系数为 {c}")
节点 1 的聚类系数为 1.0
节点 2 的聚类系数为 1.0
节点 3 的聚类系数为 0.3333333333333333
节点 4 的聚类系数为 0
# 1. 计算节点的k ,ki:
# test_node : 3
node = 3
# 邻居
neighbors = list(G.neighbors(node))
# 度
k = len(neighbors)
k # 节点3对应的k为3
3
# 2. ei的计算
neighbors
for i in range(k):for j in range(i + 1, k):if G.has_edge(neighbors[i], neighbors[j]):# print(neighbors[i], neighbors[j])triplets += 1
triplets # 节点3对应的ei为3
2
节点的聚类系数
# 计算每个节点的聚类系数
for node in G.nodes():# 获取节点的邻居节点neighbors = list(G.neighbors(node))k = len(neighbors)if k < 2:# 如果邻居节点数少于 2,聚类系数为 0clustering = 0else:# 计算节点的三元组数量triplets = 0for i in range(k):for j in range(i + 1, k):if G.has_edge(neighbors[i], neighbors[j]):triplets += 1# 计算聚类系数clustering = 2 * triplets / (k * (k - 1))print(f"节点 {node} 的聚类系数为 {clustering}")
节点 1 的聚类系数为 1.0
节点 2 的聚类系数为 1.0
节点 3 的聚类系数为 0.3333333333333333
节点 4 的聚类系数为 0
整个网络的聚类系数C
nx.average_clustering(G=G)
0.5833333333333334
相关文章:

networkX-03-连通度、全局网络效率、局部网络效率、聚类系数计算
文章目录 1.连通度1.1 检查图是否连通1.2 检查有向图是否为强连通1.3 点连通度、边连通度: 2.网络效率2.1全局效率2.2 局部效率2.2.1 查找子图2.2.3 局部效率源码分析 3.聚类系数(Clustering Coefficient)3.1 聚类系统源码分析 教程仓库地址&…...
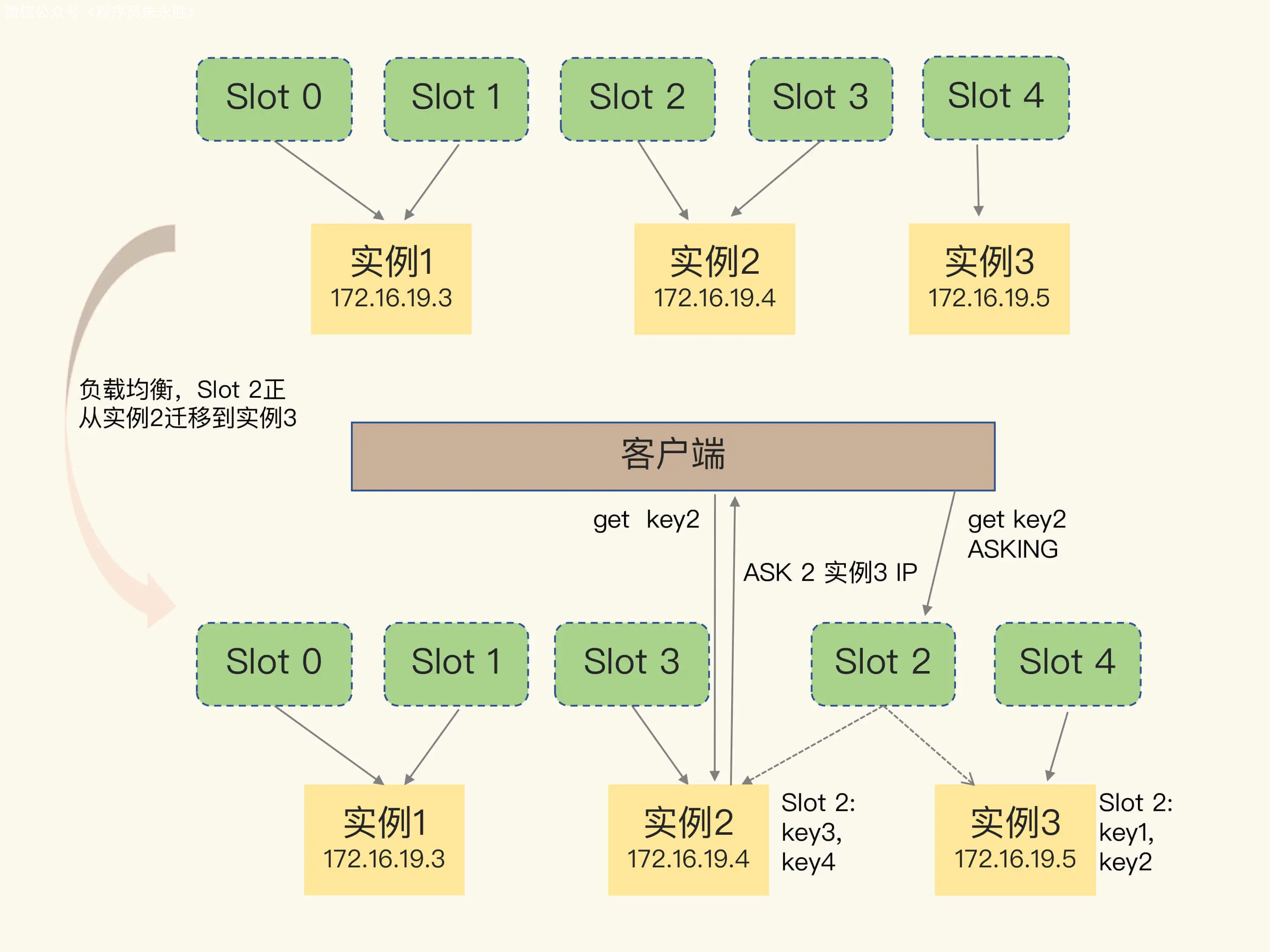
【深入解读Redis系列】Redis系列(五):切片集群详解
首发博客地址 https://blog.zysicyj.top/ 系列文章地址[1] 如果 Redis 内存很大怎么办? 假设一台 32G 内存的服务器部署了一个 Redis,内存占用了 25G,会发生什么? 此时最明显的表现是 Redis 的响应变慢,甚至非常慢。 这…...

无涯教程-JavaScript - NORMDIST函数
NORMDIST函数替代Excel 2010中的NORM.DIST函数。 描述 该函数返回指定均值和标准差的正态分布。此功能在统计中有非常广泛的应用,包括假设检验。 语法 NORMDIST(x,mean,standard_dev,cumulative)争论 Argument描述Required/OptionalXThe value for which you want the dis…...

递归应用判断是否循环引用
var data await _IDBInstance.DBOperation.QueryAsync<FormulaReference>(sql);//向上查询引用公式 List<FormulaReference> GetSonNode(long id, List<FormulaReference> nodeList, List<long> path null){if (path null){path new List<long…...

使用nginx-lua配置统一url自动跳转到hadoop-ha集群的active节点
下载安装nginx所用的依赖 yum -y install gcc zlib zlib-devel pcre-devel openssl openssl-devel下载nginx wget http://nginx.org/download/nginx-1.12.2.tar.gz tar -xvf nginx-1.12.2.tar.gz稍后安装nginx 安装lua语言 yum install readline-develcurl -R -O http://w…...
AJAX学习笔记2发送Post请求
AJAX学习笔记1发送Get请求_biubiubiu0706的博客-CSDN博客 继续 AJAX发送POST请求 无参数 测试 改回来 测试 AJAX POST请求 请求体中提交参数 测试 后端打断点 如何用AJAX模拟form表单post请求提交数据呢? 设置请求头必须在open之后,send之前 请求头里的设置好比…...

产品团队的需求分析指南
需求分析是软件开发流程中需求识别与管理的关键环节,需求分析的目的在于确保所有产品需求准确地代表了利益相关者的需求和要求。选择合适的需求分析方式可以帮助我们获取准确的产品需求,从而保证我们所交付的成果与利益相关者预期相符。 一、什么是需求…...
)
Python算法——排序算法(冒泡、选择、插入、快速、堆排序、并归排序、希尔、计数、桶排序、基数排序)
本文章只展示代码实现 ,原理大家可以参考: https://zhuanlan.zhihu.com/p/42586566 一、冒泡排序 def bubble_sort(lst):for i in range(len(lst) - 1): # 表示第i趟exchange False # 每一趟做标记for j in range(len(lst)-i-1): # 表示箭头if ls…...
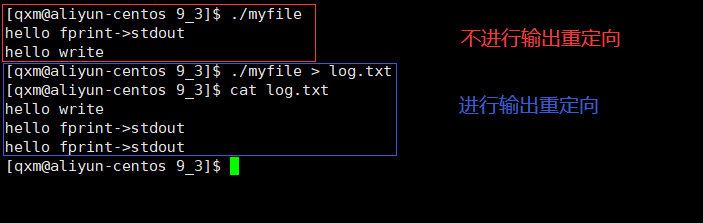
[Linux]文件描述符(万字详解)
[Linux]文件描述符 文章目录 [Linux]文件描述符文件系统接口open函数close函数write函数read函数系统接口与编程语言库函数的关系 文件描述符文件描述符的概念文件数据交换的原理理解“一切皆文件”进程默认文件描述符文件描述符和编程语言的关系 重定向输出重定向输入重定向追…...
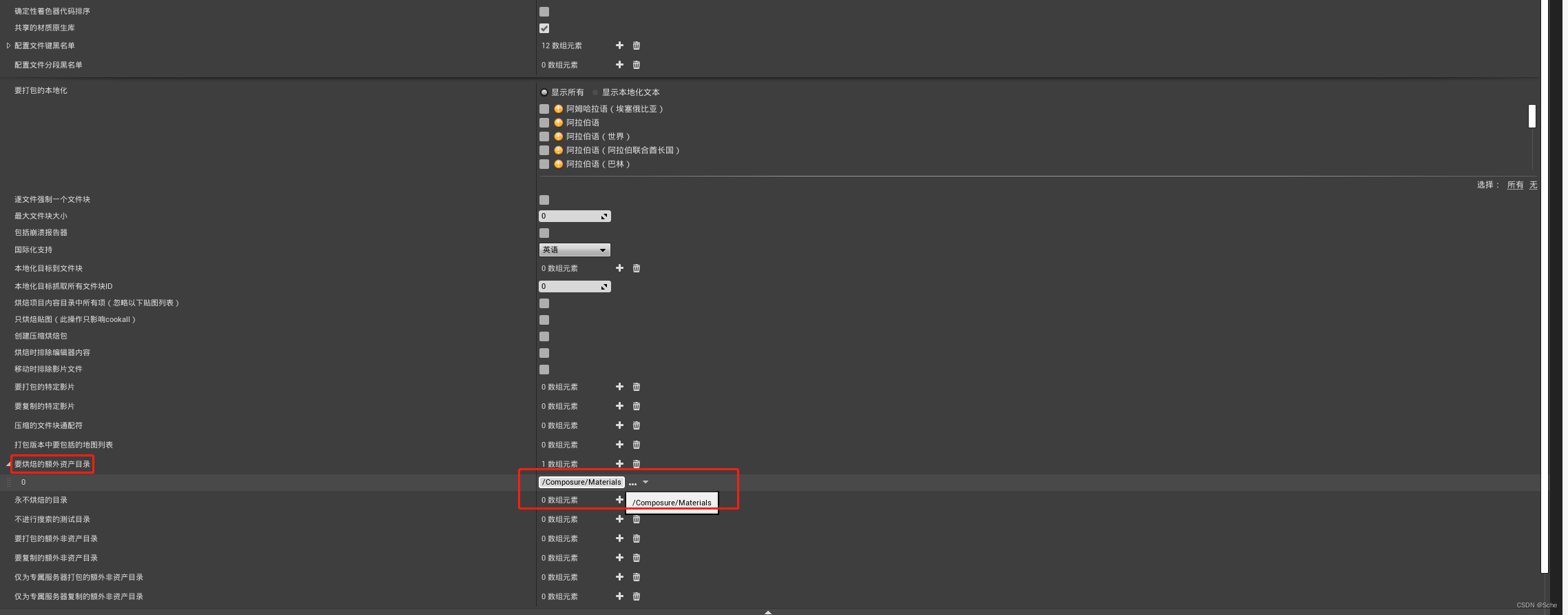
RenderTarget导出成图片,CineCamera相机
一、获取Cinecamera相机图像 1.1、启用UE自带插件 1.2、在UE编辑器窗口栏找到Composure合成,打开窗口 1. 3、右键空白处,新建合成,默认名称为 0010_comp;再右键新建的 0010_comp,新建图层元素 CGLayer层,默…...
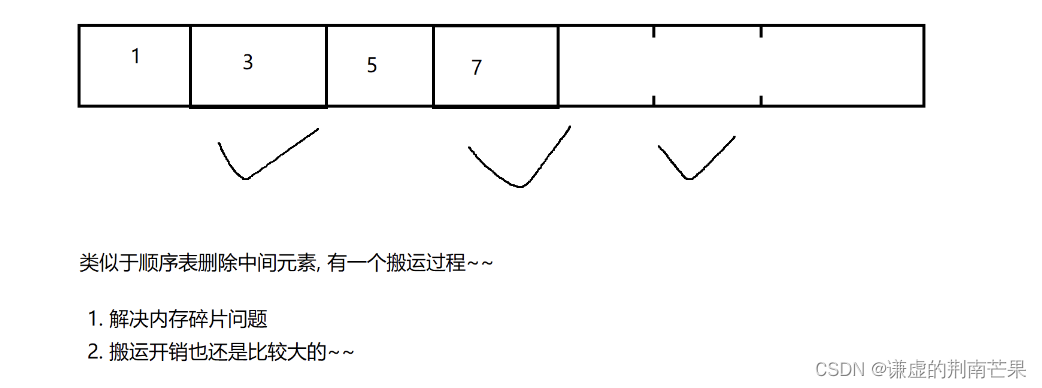
深入探讨Java虚拟机(JVM):执行流程、内存管理和垃圾回收机制
目录 什么是JVM? JVM 执行流程 JVM 运行时数据区 堆(线程共享) Java虚拟机栈(线程私有) 什么是线程私有? 程序计数器(线程私有) 方法区(线程共享) JDK 1.8 元空…...
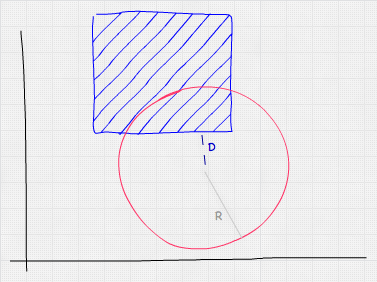
3D 碰撞检测
推荐:使用 NSDT场景编辑器快速搭建3D应用场景 轴对齐边界框 与 2D 碰撞检测一样,轴对齐边界框 (AABB) 是确定两个游戏实体是否重叠的最快算法。这包括将游戏实体包装在一个非旋转(因此轴对齐)的框中&#…...
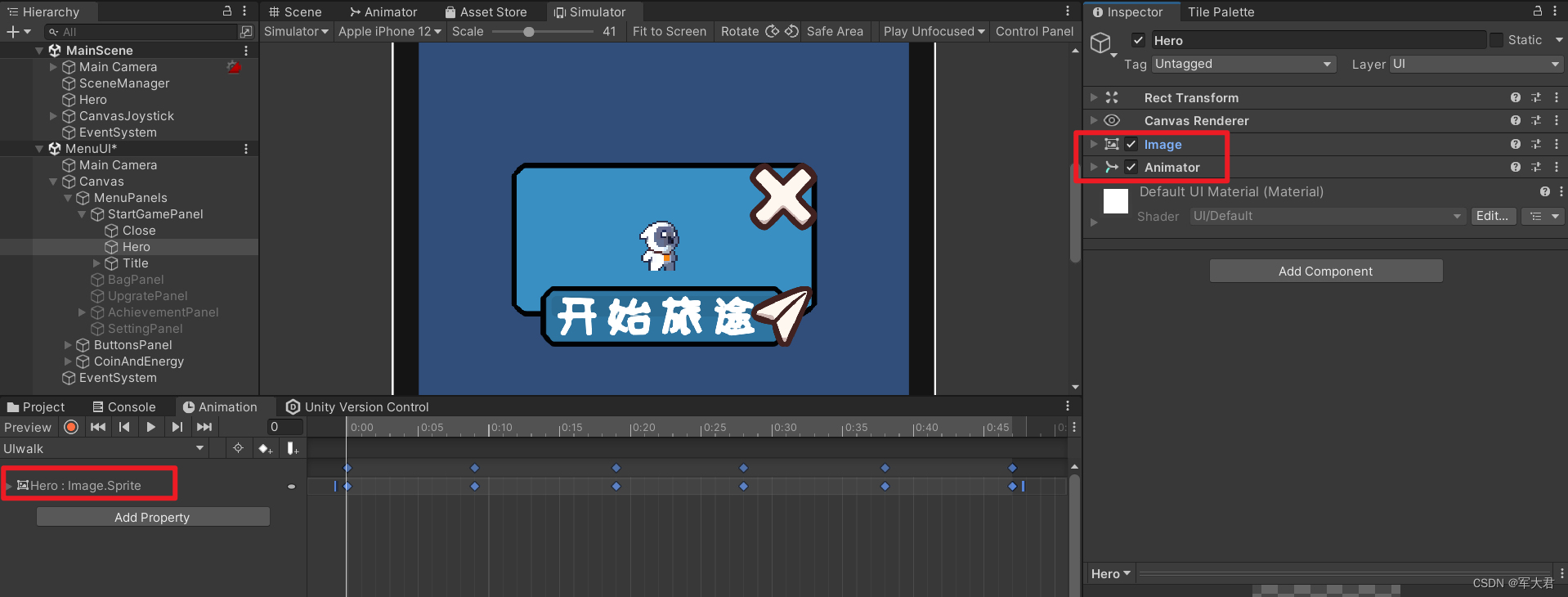
Unity Canvas动画不显示的问题
问题描述: 我通过角色创建了一个walk的动画,当我把这个动画给到Canvas里面的一个image上,这个动画就不能正常播放了,经过一系列的查看我才发现,canvas里面动画播放和非canvas得动画播放,他们的动画参数是不一样的。一个…...

NSSCTF2nd与羊城杯部分记录
文章目录 前言[NSSCTF 2nd]php签到[NSSCTF 2nd]MyBox[NSSCTF 2nd]MyHurricane[NSSCTF 2nd]MyJs[NSSCTF 2nd]MyAPK羊城杯[2023] D0nt pl4y g4m3!!!羊城杯[2023]ezyaml羊城杯[2023]Serpent羊城杯[2023]EZ_web羊城杯[2023]Ez_misc总结 前言 今天周日,有点无聊没事干&a…...

数据库(一) 基础知识
概述 数据库是按照数据结构来组织,存储和管理数据的仓库 数据模型 数据库系统的核心和基础是数据模型,数据模型是严格定义的一组概念的集合。因此数据模型一般由数据结构、数据操作和完整性约束三部分组成。数据模型主要分为三种:层次模型,网状模型和关…...
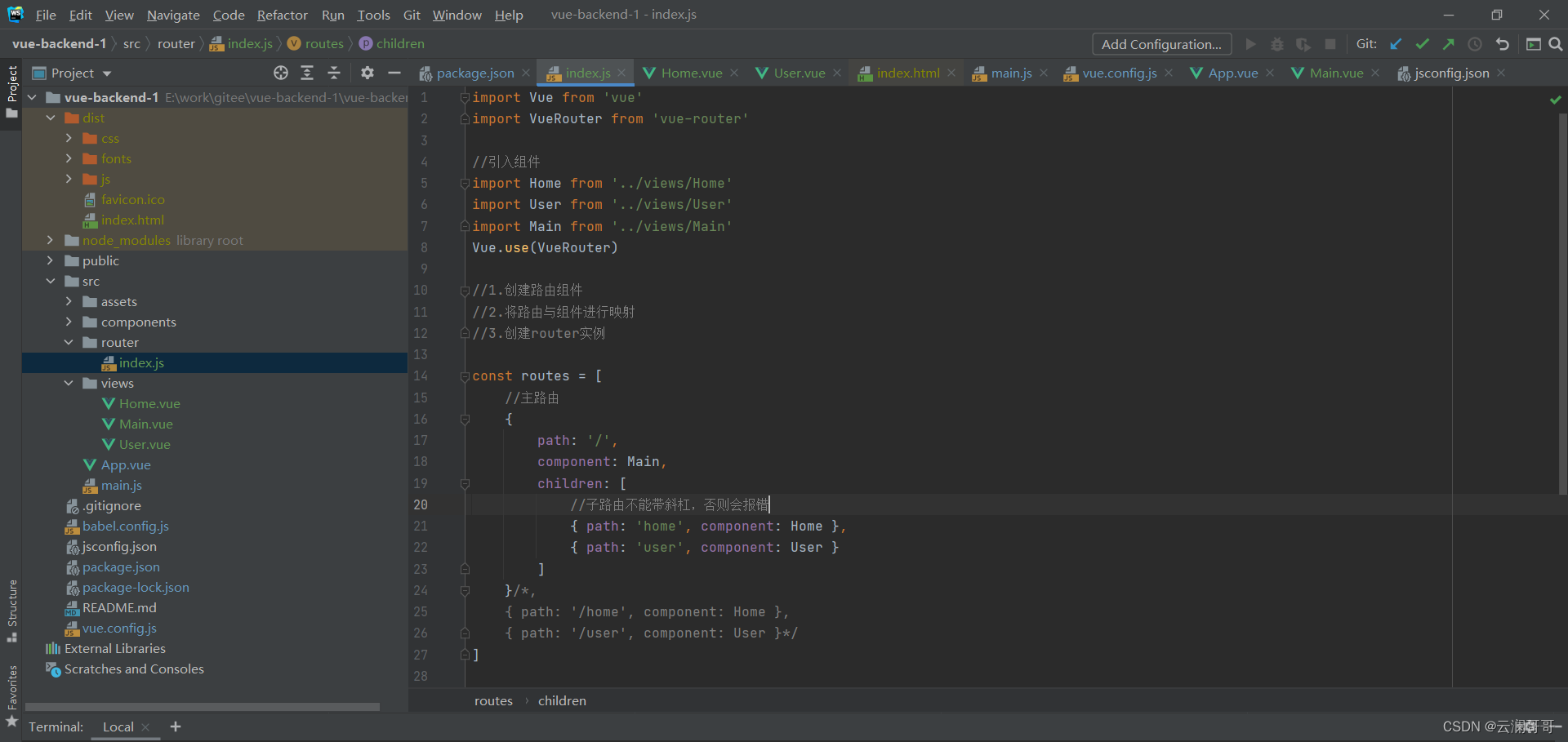
vue从零开始学习
npm install慢解决方法:删掉nodel_modules。 5.0.3:表示安装指定的5.0.3版本 ~5.0.3:表示安装5.0X中最新的版本 ^5.0.3: 表示安装5.x.x中最新的版本。 yarn的优点: 1.速度快,可以并行安装 2.安装版本统一 项目搭建: 安装nodejs查看node版本:node -v安装vue clie : np…...
dji uav建图导航系列(三)模拟建图、导航
前面博文【dji uav建图导航系列()建图】、【dji uav建图导航系列()导航】 使用真实无人机和挂载的激光雷达完成建图、导航的任务。 当需要验证某一个slam算法时,我们通常使用模拟环境进行测试,这里使用stageros进行模拟测试,实际就是通过模拟器,虚拟一个带有传感器(如…...
PixelSNAIL论文代码学习(1)——总体框架和平移实现因果卷积
文章目录 引言正文目录解析README.md阅读Setup配置Training the model训练模型Pretrained Model Check Point预训练的模型训练方法 train.py文件的阅读model.py文件阅读h12_noup_smallkey_spec模型定义_base_noup_smallkey_spec模型实现一、定义因果卷积过程通过平移实现因果卷…...

Python大数据处理利器之Pyspark详解
摘要: 在现代信息时代,数据是最宝贵的财富之一,如何处理和分析这些数据成为了关键。Python在数据处理方面表现得尤为突出。而pyspark作为一个强大的分布式计算框架,为大数据处理提供了一种高效的解决方案。本文将详细介绍pyspark…...

S905L3A(M401A)拆解, 运行EmuELEC和Armbian
关于S905L3A / S905L3AB S905Lx系列没有公开资料, 猜测是Amlogic用于2B的芯片型号, 最早的 S905LB 是 S905X 的马甲, 而这个 S905L3A/S905L3AB 则是 S905X2 的马甲, 因为在性能评测里这两个U的得分几乎一样. S905L3A/S905L3AB 和 S905X2, S905X3 一样 GPU 是 G31, 相比前一代的…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...
