重要性采样
重要性采样
前言
离散型随机变量 X X X,我们可以通过以下方法求取其期望:
-
直接计算法,需要知道概率分布:
E ( X ) = ∑ x ∈ X [ p ( x ) ⋅ x ] \mathbb{E}(X)=\sum_{x\in X}\left[p(x)\cdot x\right] E(X)=x∈X∑[p(x)⋅x] -
采样计算,这时即使 X X X概率分布未知,依据大数定律,当采样次数够大时,仍然可以求取期望
E ( X ) = 1 n lim n → + ∞ ∑ i = 0 n − 1 x i \mathbb{E}(X)=\frac{1}{n}\lim_{n\to +\infty}\sum_{i=0}^{n-1} x_i E(X)=n1n→+∞limi=0∑n−1xi
连续型随机变量 X X X
- 直接计算,需要 f f f表达式
E ( X ) = ∫ x x ⋅ f ( x ) d x \mathbb{E}(X)=\int_x x\cdot f(x)dx E(X)=∫xx⋅f(x)dx
- 抽样(蒙特卡洛积分估计),这里不多做介绍
重要性采样
思想:如果已知随机变量 X ∼ p 0 X\sim p_0 X∼p0,在 p 0 p_0 p0下随机采样了一批数据 { x i } ∼ p 0 \{x_i\}\sim p_0 {xi}∼p0,现在要求随机变量 X ∼ p 1 X\sim p_1 X∼p1下的期望,则:
E X ∼ p 1 [ X ] = ∑ x p 1 ( x ) ⋅ x = ∑ x p 0 ( x ) p 1 ( x ) p 0 ( x ) ⋅ x = E X ∼ p 0 [ f ( X ) ] \mathbb{E}_{X\sim p_1}[X]=\sum_x p_1(x)\cdot x=\sum_x p_0(x) \frac{p_1(x)}{p_0(x)}\cdot x=\mathbb{E}_{X\sim p_0}[f(X)] EX∼p1[X]=x∑p1(x)⋅x=x∑p0(x)p0(x)p1(x)⋅x=EX∼p0[f(X)]
那么就有如下几个问题:
-
对于离散型随机变量,为什么 p 1 ( x ) p_1(x) p1(x)已知,不直接计算期望呢?
- 因为有时候我们已经根据 p 0 p_0 p0采样了一些数据,再用 p 1 p_1 p1重新采样计算一遍,会增加很多计算量。
- 因为有些时候不方便对 p 1 p_1 p1采样
- 在强化学习中,我们根据一个策略采样,通过重要性采样可以求出另一个策略的期望,是一种On Policy向Off Policy转换的思想。
-
对于连续型随机变量,为什么 p 1 ( x ) p_1(x) p1(x)已知,不直接计算期望呢?
理论上不可能完全求出概率密度函数,所以无法从理论上计算期望,只能估计。
例如,如果我们通过神经网络来表示 f f f,那么对任意的输入 x x x,我们都可以求出 f ( x ) f(x) f(x),但是这并不代表我们求出 f f f的函数表达式,更无法进一步求积分。我们只是能从数值上计算出 f ( x ) f(x) f(x),神经网络本身就是一个黑盒。
综上所述,重要性采样使得我们能够从behavior policy采样,然后去估计target policy的期望,从而使得On Policy的算法转换为Off Policy
相关文章:

重要性采样
重要性采样 前言 离散型随机变量 X X X,我们可以通过以下方法求取其期望: 直接计算法,需要知道概率分布: E ( X ) ∑ x ∈ X [ p ( x ) ⋅ x ] \mathbb{E}(X)\sum_{x\in X}\left[p(x)\cdot x\right] E(X)x∈X∑[p(x)⋅x] 采…...

说说Omega架构
分析&回答 Omega架构我们暂且称之为混合数仓。 什么是ECS设计模式 在谈我们的解法的时候,必须要先提ECS的设计模式。 简单的说,Entity、Component、System分别代表了三类模型。 实体(Entity):实体是一个普通的对象。通常,…...

高忆管理:光刻胶概念强势拉升,同益股份、格林达涨停
光刻胶概念5日盘中强势拉升,截至发稿,同益股份、格林达涨停,波长光电、晶瑞电材涨超7%,容大感光涨逾5%,华懋科技、茂莱光学、苏大维格、南大光电等均走强。 音讯面上,据新加坡《联合早报》网站9月2日报导&…...

计算机图形学线性代数相关概念
Transformation(2D-Model) Scale(缩放) [ x ′ y ′ ] [ s 0 0 s ] [ x y ] (等比例缩放) \left[ \begin{matrix} x \\ y \end{matrix} \right] \left[ \begin{matrix} s & 0 \\ 0 & s \end{matrix} \right] \left[ \begin{matrix} x \\ y \en…...

开源PHP 代挂机源码,可对接QQ、网易云、哔哩哔哩、QQ空间、等级加速等等
本程序运行环境PHP5.6 95dg/config.php修改系统数据库 进入数据库绑定 你搭建的域名即可 部署完成 进入数据库 找到data 输入绑定授权域名即可进行授权打开此网站 网站是无对接接口 需要您自行找对接接口即可 本源码有点乱 有实力的铁铁 可以修改一下哦!...

【仿牛客论坛java项目】第五章 Kafka,构建TB级异步消息系统:阻塞队列、Kafka入门、Spring整合Kafka、发送系统通知、显示系统通知
这里写自定义目录标题 一、阻塞队列简单的阻塞队列测试案例总结阻塞队列 二、Kafka入门1、基础知识Kafka术语消息队列实现方式两种 2、配置3、启动全部命令启动 zookeeper 服务器再启动 kafka 服务器创建Topic关闭 4、总结Kafka的特点Kafka的术语 三、 Spring整合Kafka导入依赖…...
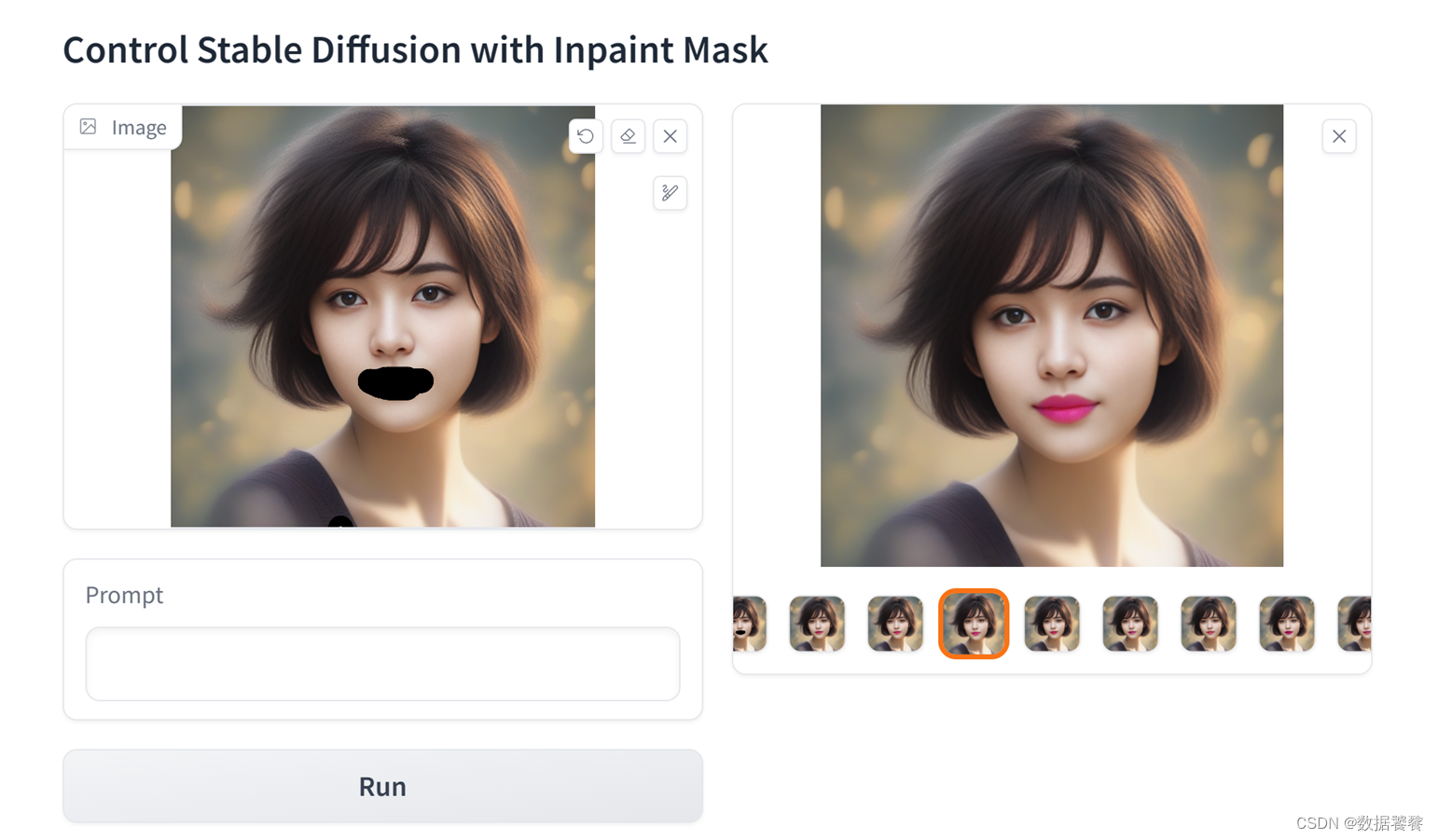
【AIGC专题】Stable Diffusion 从入门到企业级实战0401
一、概述 本章是《Stable Diffusion 从入门到企业级实战》系列的第四部分能力进阶篇《Stable Diffusion ControlNet v1.1 图像精准控制》第01节, 利用Stable Diffusion ControlNet Inpaint模型精准控制图像生成。本部分内容,位于整个Stable Diffusion生…...
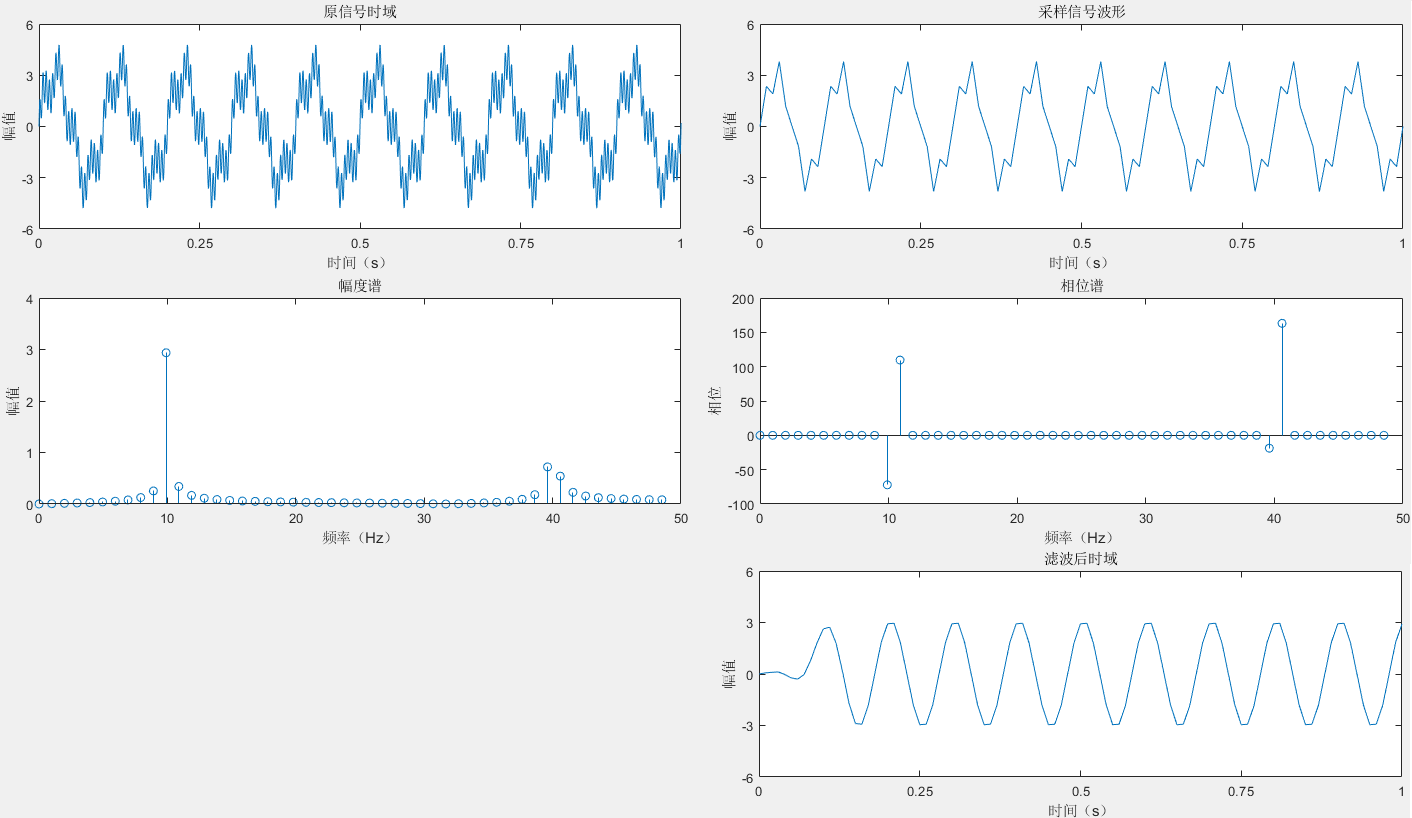
Matlab信号处理1:模拟去除信号噪声
由于工作内容涉及信号系统、信号处理相关知识,本人本硕均为计算机相关专业,专业、研究方向均未涉及信号相关知识,因此需进行系统地学习。之前已将《信号与系统》快速过了一遍,但感觉较抽象且理解较浅显。在此系统地学习如何使用Ma…...

Bootstrap的行、列布局设计(网络系统设计)
目录 00-基础知识01-等宽列布局02-指定某一列的宽度03-根据内容自动改变列的宽度04-五种预定义列宽度 .col、.col-sm-*、.col-md-*、.col-lg-*、.col-xl-*05-不同视口宽度按不同的分列方案划分06-删除列内容的盒模型的外边距07-超过12列怎么办?08-重新排列各列的顺序…...

1.1 计算机网络在信息时代中的作用
思维导图: 正文: 我的理解: 这段话是一本书或课程的第一章简介,它的目的是为读者或学生提供一个关于计算机网络基础知识的框架或大纲。 首先,它强调了这章是整本书的一个概览,会先介绍计算机网络在信息时…...

mysql CONCAT使用
问题 有一个查找数据的mysql语句:SELECT DISTINCT fund_id,version,statistic_date FROM fund_nv_divident WHERE version ( SELECT max(version) FROM fund_nv_divident) and statistic_date > ‘2023-06-04’ and fund_id not in (SELECT DISTINCT fund_id f…...

maven基础学习
什么是maven 构建 依赖 maven核心概念坐标 在黑窗口使用maven命令生成maven工程 pom.xml 想导入哪个jar包把它的坐标放到dependency里就可以 maven核心概念POM maven核心概念约定的目录结构 执行maven的构建命令 清理操作,clean 编译操作 compile 测试操作 test 打包…...

uniapp移动端地图,点击气泡弹窗并实现精准定位
记录移动端地图map组件的使用 需求记录: 移动端地图部分需要展示两个定位点,上报点及人员定位点。通过右上角的两个按钮实现地图定位。点击对应定位气泡,弹出定位点的信息。 效果图如下: map在nvue中的使用。直接用nvue可以直接…...

2023牛客暑期多校训练营7 CI「位运算」「根号分治+容斥」
C-Beautiful Sequence_2023牛客暑期多校训练营7 (nowcoder.com) 题意: 给定一个b序列,a序列满足 a [ i − 1 ] < a [ i ] a[i-1]<a[i] a[i−1]<a[i]且 a [ i ] ⊕ a [ i 1 ] b [ i ] a[i]\oplus a[i1]b[i] a[i]⊕a[i1]b[i],求字…...

YOLOv5算法改进(10)— 替换主干网络之GhostNet
前言:Hello大家好,我是小哥谈。GhostNet是一种针对计算机视觉任务的深度神经网络架构,它于2020年由中国科学院大学的研究人员提出。GhostNet的设计目标是在保持高精度的同时,减少模型的计算和存储成本。GhostNet通过引入Ghost模块…...

Android Canvas的使用
android.graphics.Canvas 一般在自定义View中,重写 onDraw(Canvas canvas) 方法时用到。 /*** Implement this to do your drawing.** param canvas the canvas on which the background will be drawn*/Overrideprotected void onDraw(Canvas canvas) {super.onDra…...
)
AI批量写文章伪原创:基于ChatGPT长文本模型,实现批量改写文章、批量回答问题(长期更新)
import traceback import openai import osopenai.api_key = ""conversation=[{"role": "system", "content": "You are a helpful assistant."}] max_history_len = 20 first_message = Nonedir = rJ:\ai\input #要改写的文…...

git常用场景记录 | 拉取远程分支A合并到本地分支B - 删除上一次的commit
文章目录 git常用场景记录拉取远程分支A合并到本地分支B本地分支B存在未add与commit的代码 删除上一次的commit已经push到远程库 git常用场景记录 doing,最后更新9.5 拉取远程分支A合并到本地分支B 需求描述 在团队合作时,我自己的本地分支B功能已经实现…...
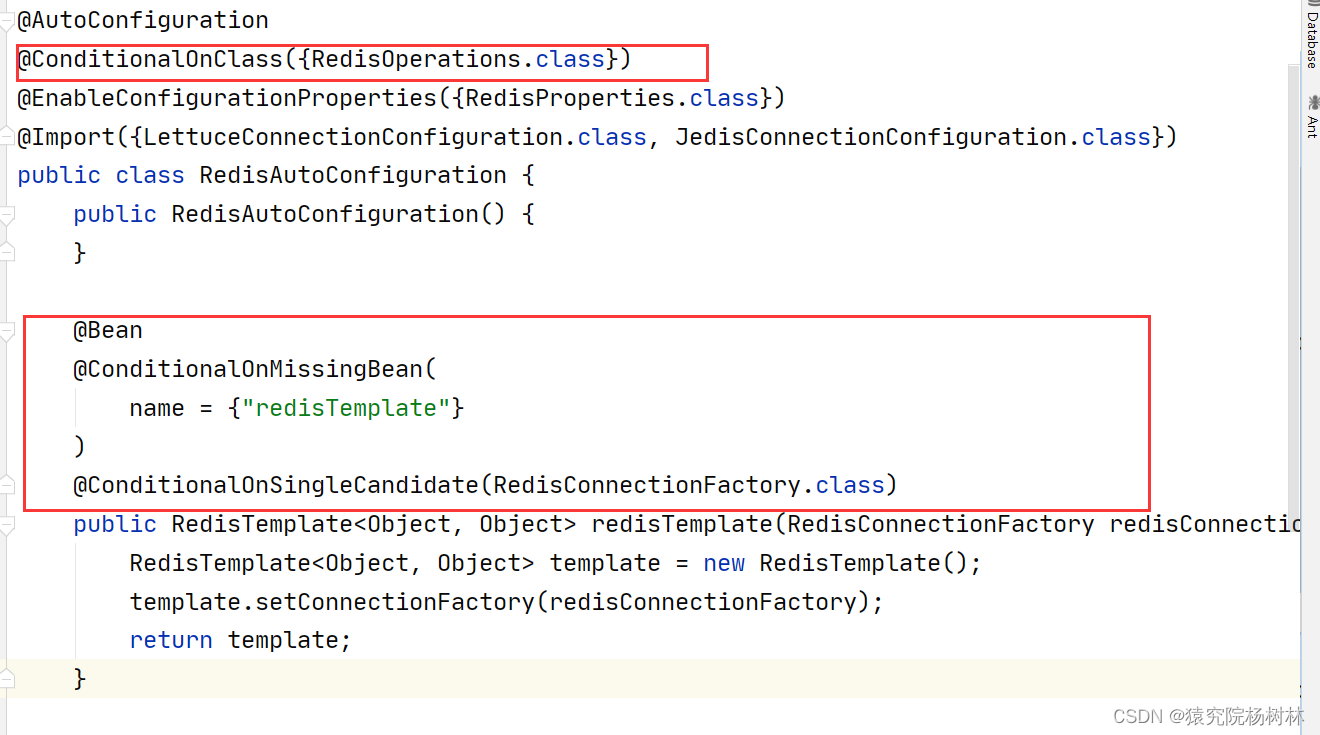
源码角度解析SpringBoot 自动配置
文章目录 前言一、了解相关注解1.Condition注解2.Enable注解 二、SpringBoot自动配置1.SpringBootApplication注解2.SpringBootConfiguration注解3.EnableAutoConfiguration注解4.Conditional注解 总结 前言 Spring Boot 自动配置是 Spring Boot 的核心特性之一,它…...

【原创】H3C路由器OSPF测试
网络拓扑图 路由器配置: 路由器1上接了4跟线,分别为这四个接口配置IP地址。 # interface GigabitEthernet0/0/0port link-mode routecombo enable copperip address 2.1.1.2 255.255.255.0 # interface GigabitEthernet0/0/1port link-mode routecombo…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
