JAVA String 二维的字符串数组 String[][]
String[][] 表示一个二维的字符串数组,也可以称为字符串矩阵。它是由多个一维的字符串数组组成的,每个一维数组都表示矩阵中的一行。
在 Java 中,可以使用如下方式声明和初始化一个二维字符串数组:
String[][] matrix = new String[rowCount][columnCount];其中 rowCount 表示矩阵的行数,columnCount 表示矩阵的列数。这里的 rowCount 和 columnCount 可以是任意非负整数,用于定义矩阵的大小。
例如,创建一个 3 行 2 列的二维字符串数组并初始化:
String[][] matrix = new String[3][2];可以通过索引访问和修改二维字符串数组中的元素。索引从 0 开始,第一个索引指定行,第二个索引指定列。示例如下:
matrix[0][0] = "A";
matrix[0][1] = "B";
matrix[1][0] = "C";
matrix[1][1] = "D";
matrix[2][0] = "E";
matrix[2][1] = "F";
System.out.println(matrix[1][1]); // 输出 "D"可以通过循环遍历二维数组来访问或修改其中的所有元素。示例如下:
for (int i = 0; i < rowCount; i++)
{ for (int j = 0; j < columnCount; j++){ System.out.println(matrix[i][j]); }
}需要根据具体的需求和业务逻辑来使用二维字符串数组,它可以在许多场景中用于存储和操作二维数据。
相关文章:

JAVA String 二维的字符串数组 String[][]
String[][] 表示一个二维的字符串数组,也可以称为字符串矩阵。它是由多个一维的字符串数组组成的,每个一维数组都表示矩阵中的一行。 在 Java 中,可以使用如下方式声明和初始化一个二维字符串数组: String[][] matrix new Strin…...

【Unity3D赛车游戏优化篇】【九】Unity中如何让汽车丝滑漂移?
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...

el-dialog设置高度、使用resetFields清除表单项无效问题
初学者容易踩坑的的el-dialog、el-form问题 1. el-dialog设置高度2. el-form中表单项对不齐3. 使用resetFields清除表单项无效 1. el-dialog设置高度 在el-dialog中里面添加一个div设置固定高度,或者限制最小的高度。 <el-dialogtitle"选择图标"v-mod…...

MySql切换到达梦数据库,各种问题解决记录
参考官方文档: https://eco.dameng.com/document/dm/zh-cn/sql-dev/practice-func.html 1. 关键字导致的报错:如ref,comment,top,domain等 Error -2007: 第 1 行, 第 117 列[ref]附近出现错误: 语法分析出错解决方案:修改关键字即可 2. 查…...

2023开学礼山东财经大学《乡村振兴战略下传统村落文化旅游设计》许少辉新财经图书馆
2023开学礼山东财经大学《乡村振兴战略下传统村落文化旅游设计》许少辉新财经图书馆...

vscode中使用eslint+prettier的配置
eslintprettiervscode自动保存用起来感觉非常爽快。 一般来说,安装eslintprettier插件,然后使用相关脚手架配套的eslintprettier,无法自动格式代码,每次都需要执行格式化命令。这里贴出保存自动格式化代码的setting.json。 // .…...
HTML 标签讲解
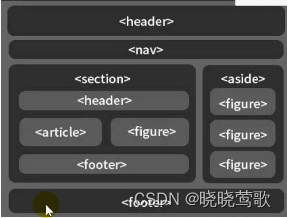
HTML 标签讲解 HTML 语言结构根元素元数据元素主体根元素大纲元素文本内容语义化内联文本图像与多媒体编辑标识table表格内容表单内容table表单 HTML 语言结构 Markup (标记、标签)用来容纳和描述内容 严格意义上,标签是指开始标签…...

ue5 小知识点 ue的world type,pie editor game
说明以该命令行模式启动游戏的前提下的两个问题: 1.WITH_EDITOR中的代码会被编译 2.由于没有在编辑器中(即没有打开虚幻编辑器),所以GIsEditor为false WITH_EDITOR和WITH_EDITORONLY_DATA的区别 在论坛中找到的答案: WITH_EDITORONLY_DAT…...

两表union 如何保证group by 字段唯一
当要计算的指标可能来源多个表时,可能会使用到union all把不同的表中计算的指标合起来。关于union all使用条件:两个要联合的SQL语句 字段个数必须一样,而且字段类型要“相容”(一致) 另外,回顾union和uni…...

【⑰MySQL】 变量 | 循环 | 游标 | 处理程序
前言 ✨欢迎来到小K的MySQL专栏,本节将为大家带来MySQL变量 | 循环 | 游标 | 处理程序的分享✨ 目录 前言1. 变量1.1系统变量1.2 用户变量 2. 定义条件与处理程序2.1 案例分析2.2 定义条件2.3 定义处理程序2.4 案例解决 3. 流程控制3.1 分支结构3.2 循环结构3.3 跳转…...
如何在arXiv上发表一篇文章
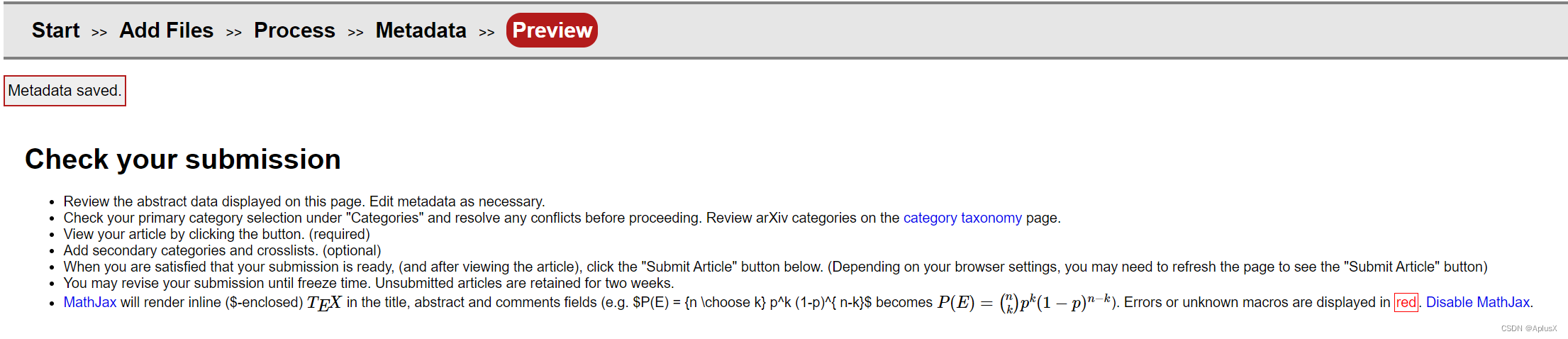
目录 1. 初始信息确认2. 提交论文文件3. 论文编译结果4. 补充论文信息5. 总览 1. 初始信息确认 版权问题需要根据个人情况选择。 IEEE, Elsevier, BioMed Central, 这几个出版商都允许在投稿之前挂文章到arXiv下。通常是选择: arXiv.org perpetual, non-exclusive l…...

重要性采样
重要性采样 前言 离散型随机变量 X X X,我们可以通过以下方法求取其期望: 直接计算法,需要知道概率分布: E ( X ) ∑ x ∈ X [ p ( x ) ⋅ x ] \mathbb{E}(X)\sum_{x\in X}\left[p(x)\cdot x\right] E(X)x∈X∑[p(x)⋅x] 采…...

说说Omega架构
分析&回答 Omega架构我们暂且称之为混合数仓。 什么是ECS设计模式 在谈我们的解法的时候,必须要先提ECS的设计模式。 简单的说,Entity、Component、System分别代表了三类模型。 实体(Entity):实体是一个普通的对象。通常,…...

高忆管理:光刻胶概念强势拉升,同益股份、格林达涨停
光刻胶概念5日盘中强势拉升,截至发稿,同益股份、格林达涨停,波长光电、晶瑞电材涨超7%,容大感光涨逾5%,华懋科技、茂莱光学、苏大维格、南大光电等均走强。 音讯面上,据新加坡《联合早报》网站9月2日报导&…...

计算机图形学线性代数相关概念
Transformation(2D-Model) Scale(缩放) [ x ′ y ′ ] [ s 0 0 s ] [ x y ] (等比例缩放) \left[ \begin{matrix} x \\ y \end{matrix} \right] \left[ \begin{matrix} s & 0 \\ 0 & s \end{matrix} \right] \left[ \begin{matrix} x \\ y \en…...

开源PHP 代挂机源码,可对接QQ、网易云、哔哩哔哩、QQ空间、等级加速等等
本程序运行环境PHP5.6 95dg/config.php修改系统数据库 进入数据库绑定 你搭建的域名即可 部署完成 进入数据库 找到data 输入绑定授权域名即可进行授权打开此网站 网站是无对接接口 需要您自行找对接接口即可 本源码有点乱 有实力的铁铁 可以修改一下哦!...

【仿牛客论坛java项目】第五章 Kafka,构建TB级异步消息系统:阻塞队列、Kafka入门、Spring整合Kafka、发送系统通知、显示系统通知
这里写自定义目录标题 一、阻塞队列简单的阻塞队列测试案例总结阻塞队列 二、Kafka入门1、基础知识Kafka术语消息队列实现方式两种 2、配置3、启动全部命令启动 zookeeper 服务器再启动 kafka 服务器创建Topic关闭 4、总结Kafka的特点Kafka的术语 三、 Spring整合Kafka导入依赖…...
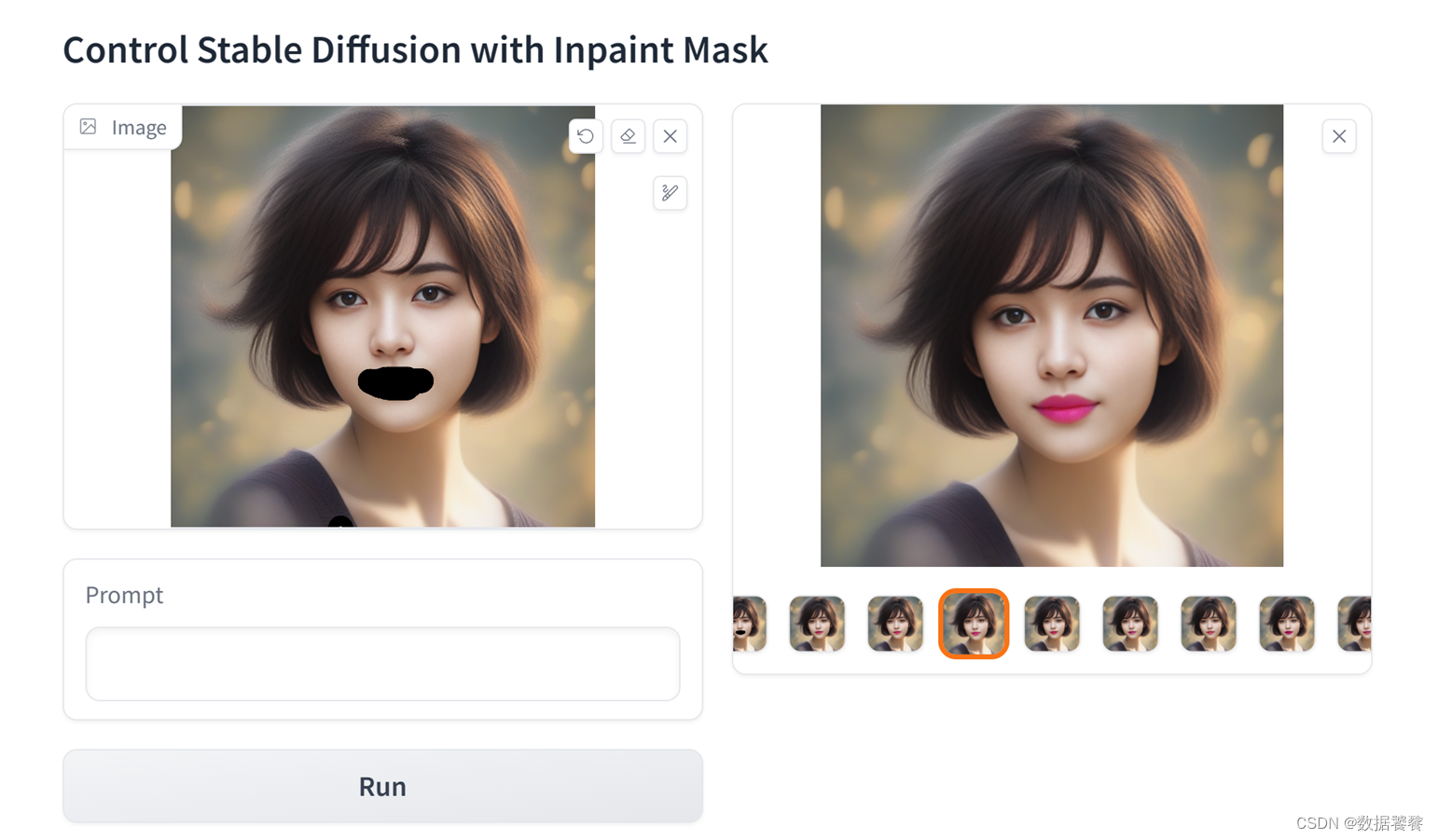
【AIGC专题】Stable Diffusion 从入门到企业级实战0401
一、概述 本章是《Stable Diffusion 从入门到企业级实战》系列的第四部分能力进阶篇《Stable Diffusion ControlNet v1.1 图像精准控制》第01节, 利用Stable Diffusion ControlNet Inpaint模型精准控制图像生成。本部分内容,位于整个Stable Diffusion生…...
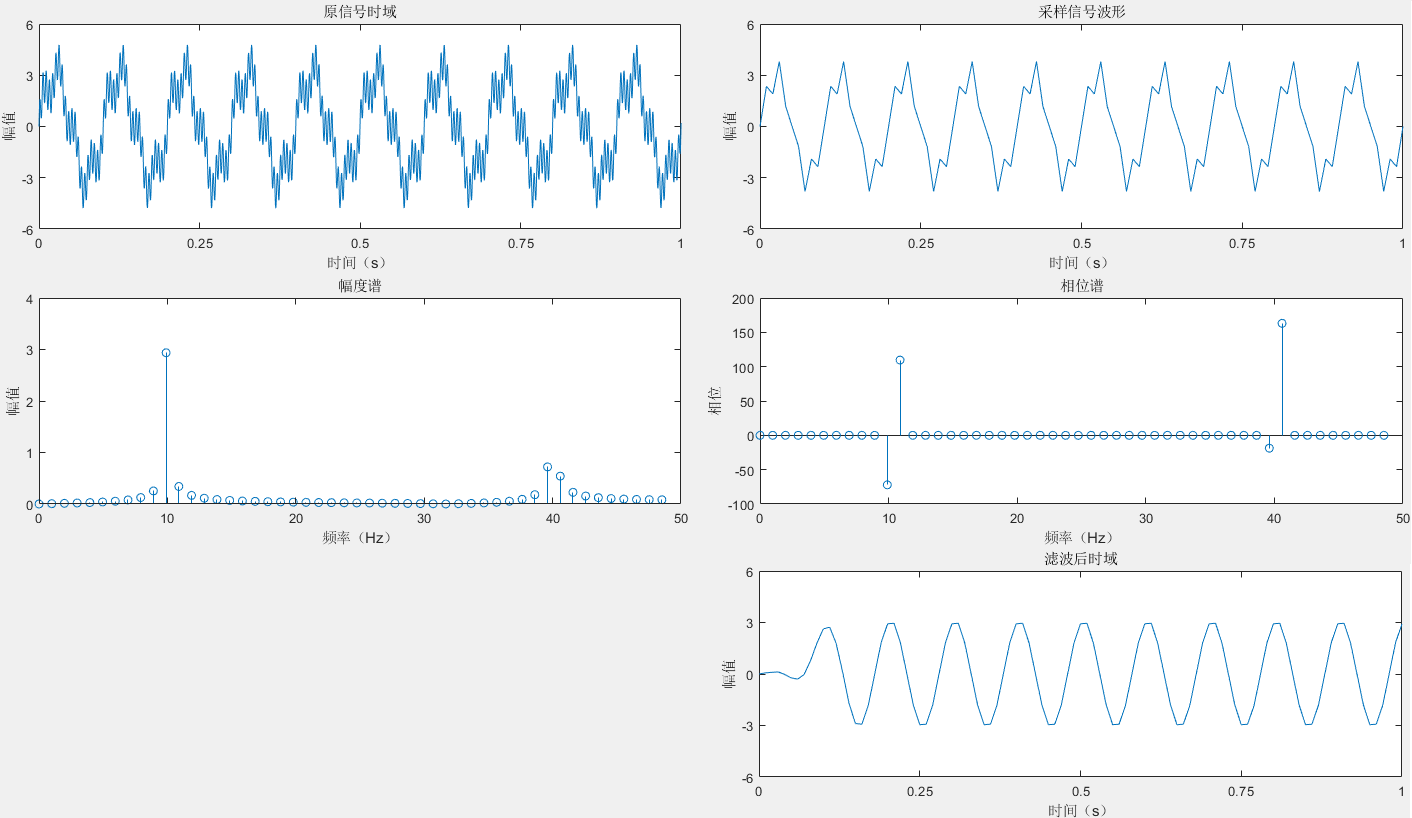
Matlab信号处理1:模拟去除信号噪声
由于工作内容涉及信号系统、信号处理相关知识,本人本硕均为计算机相关专业,专业、研究方向均未涉及信号相关知识,因此需进行系统地学习。之前已将《信号与系统》快速过了一遍,但感觉较抽象且理解较浅显。在此系统地学习如何使用Ma…...

Bootstrap的行、列布局设计(网络系统设计)
目录 00-基础知识01-等宽列布局02-指定某一列的宽度03-根据内容自动改变列的宽度04-五种预定义列宽度 .col、.col-sm-*、.col-md-*、.col-lg-*、.col-xl-*05-不同视口宽度按不同的分列方案划分06-删除列内容的盒模型的外边距07-超过12列怎么办?08-重新排列各列的顺序…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...

【R语言编程——数据调用】
这里写自定义目录标题 可用库及数据集外部数据导入方法查看数据集信息 在R语言中,有多个库支持调用内置数据集或外部数据,包括studentdata等教学或示例数据集。以下是常见的库和方法: 可用库及数据集 openintro库 该库包含多个教学数据集&a…...
