AcWing 787:归并排序
【题目来源】
https://www.acwing.com/problem/content/789/
【题目描述】
给定你一个长度为 n 的整数数列。
请你使用归并排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
【输入格式】
输入共两行,第一行包含整数 n。
第二行包含 n 个整数(所有整数均在 1∼10^9 范围内),表示整个数列。
【输出格式】
输出共一行,包含 n 个整数,表示排好序的数列。
【数据范围】
1≤n≤100000
【输入样例】
5
3 1 2 4 5
【输出样例】
1 2 3 4 5
【算法分析】
● 归并排序是一种常用且高效的排序算法,它采用分治法的思想来对序列进行排序。归并排序的基本思想是将序列分成较小的子序列,递归地对这些子序列进行排序,然后将它们合并在一起,产生最终的有序序列。归并排序模拟示意图如下所示。
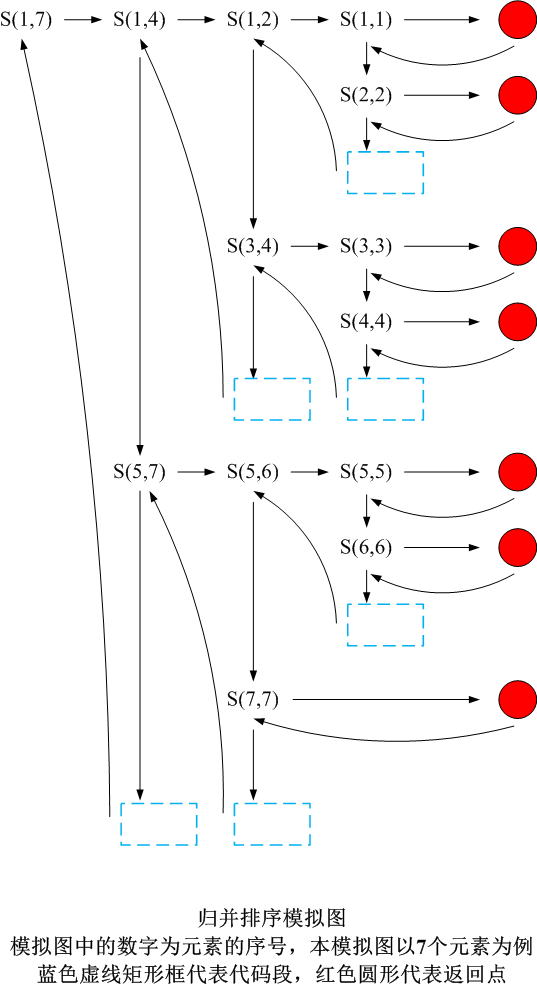
● 归并排序采用分治法的思想来对序列进行排序,它的 mid 值是取待排序列的中间位置的元素序号作为基准值。归快速排序算法 https://blog.csdn.net/hnjzsyjyj/article/details/132669946 虽然也是采用分治法的思想来对序列进行排序,但是它的 mid 值是取待排序列的中间位置的元素值作为基准值。
【算法代码】
#include <bits/stdc++.h>
using namespace std;const int maxn=1e5+5;
int a[maxn], tmp[maxn];void merge_sort(int v[],int le,int ri) {if(le>=ri) return;int mid=le+ri>>1;merge_sort(v,le,mid);merge_sort(v,mid+1,ri);int k=0;int i=le,j=mid+1;while(i<=mid && j<=ri) {if(v[i]<=v[j]) tmp[k++]=v[i++];else tmp[k++]=v[j++];}while(i<=mid) tmp[k++]=v[i++];while(j<=ri) tmp[k++]=v[j++];k=0;for(int i=le; i<=ri; i++) {a[i]=tmp[k++];}
}int main() {int n;scanf("%d",&n);for(int i=0; i<n; i++) scanf("%d",&a[i]);merge_sort(a,0,n-1);for(int i=0; i<n; i++) printf("%d ",a[i]);return 0;
}/*
in:
5
3 1 2 4 5out:
1 2 3 4 5
*/
【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/119760879
https://blog.csdn.net/hnjzsyjyj/article/details/119787188
https://blog.csdn.net/hnjzsyjyj/article/details/119768122
https://www.acwing.com/solution/content/27445/
相关文章:

AcWing 787:归并排序
【题目来源】https://www.acwing.com/problem/content/789/【题目描述】 给定你一个长度为 n 的整数数列。 请你使用归并排序对这个数列按照从小到大进行排序。 并将排好序的数列按顺序输出。【输入格式】 输入共两行,第一行包含整数 n。 第二行包含 n 个整数&#…...

SeamlessM4T—Massively Multilingual Multimodal Machine Translation
本文是LLM系列的文章,针对《SeamlessM4T—Massively Multilingual & Multimodal Machine Translation》的翻译。 SeamlessM4T:大规模语言多模态机器翻译 摘要1 引言2 多模态翻译的社会技术维度2.12.22.3 3 SeamlessAlign:自动创建语音对…...

Python数据分析-Numpy
Numpy 个人笔记,仅供参考,谢谢 导入 import numpy import numpy as np from numpy import *Numpy数组对象 引入 # 让列表1 a [1,2,3,4],b [4,5,6,7] [x1 for x in a] # 实现ab a b > [1,2,3,4,5,6,7,8] [x y for (x,y) in zip(a,b)] -------…...

【真题解析】系统集成项目管理工程师 2023 年上半年真题卷(案例分析)
本文为系统集成项目管理工程师考试(软考) 2023 年上半年真题(全国卷),包含答案与详细解析。考试共分为两科,成绩均 ≥45 即可通过考试: 综合知识(选择题 75 道,75分)案例分析(问答题 4 道,75分)案例分析(问答题*4)试题一试题二试题三试题四案例分析(问答题*4) …...

【GAMES202】Real-Time Global Illumination(in 3D)—实时全局光照(3D空间)
一、SH for Glossy transport 1.Diffuse PRT回顾 上篇我们介绍了PRT,并以Diffuse的BRDF作为例子分析了预计算的部分,包括Lighting和Light transport,如上图所示。 包括我们还提到了SH,可以用SH的有限阶近似拟合球面函数ÿ…...
金蝶云星空二开,公有云执行SQL
功能背景; 金蝶公有云执行sql工具,因官方为云部署 用户无法连接数据库增删改查 天梯维护网页仅支持增删改操作 二开单据已支持根据sql动态生成单据体 与sql可视化界面操作一致 功能实现及场景: 1.可用于公有云执行sql类操作 2.私有云部署&am…...

JAVA String 二维的字符串数组 String[][]
String[][] 表示一个二维的字符串数组,也可以称为字符串矩阵。它是由多个一维的字符串数组组成的,每个一维数组都表示矩阵中的一行。 在 Java 中,可以使用如下方式声明和初始化一个二维字符串数组: String[][] matrix new Strin…...

【Unity3D赛车游戏优化篇】【九】Unity中如何让汽车丝滑漂移?
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...

el-dialog设置高度、使用resetFields清除表单项无效问题
初学者容易踩坑的的el-dialog、el-form问题 1. el-dialog设置高度2. el-form中表单项对不齐3. 使用resetFields清除表单项无效 1. el-dialog设置高度 在el-dialog中里面添加一个div设置固定高度,或者限制最小的高度。 <el-dialogtitle"选择图标"v-mod…...

MySql切换到达梦数据库,各种问题解决记录
参考官方文档: https://eco.dameng.com/document/dm/zh-cn/sql-dev/practice-func.html 1. 关键字导致的报错:如ref,comment,top,domain等 Error -2007: 第 1 行, 第 117 列[ref]附近出现错误: 语法分析出错解决方案:修改关键字即可 2. 查…...

2023开学礼山东财经大学《乡村振兴战略下传统村落文化旅游设计》许少辉新财经图书馆
2023开学礼山东财经大学《乡村振兴战略下传统村落文化旅游设计》许少辉新财经图书馆...

vscode中使用eslint+prettier的配置
eslintprettiervscode自动保存用起来感觉非常爽快。 一般来说,安装eslintprettier插件,然后使用相关脚手架配套的eslintprettier,无法自动格式代码,每次都需要执行格式化命令。这里贴出保存自动格式化代码的setting.json。 // .…...
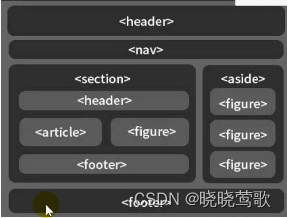
HTML 标签讲解
HTML 标签讲解 HTML 语言结构根元素元数据元素主体根元素大纲元素文本内容语义化内联文本图像与多媒体编辑标识table表格内容表单内容table表单 HTML 语言结构 Markup (标记、标签)用来容纳和描述内容 严格意义上,标签是指开始标签…...

ue5 小知识点 ue的world type,pie editor game
说明以该命令行模式启动游戏的前提下的两个问题: 1.WITH_EDITOR中的代码会被编译 2.由于没有在编辑器中(即没有打开虚幻编辑器),所以GIsEditor为false WITH_EDITOR和WITH_EDITORONLY_DATA的区别 在论坛中找到的答案: WITH_EDITORONLY_DAT…...

两表union 如何保证group by 字段唯一
当要计算的指标可能来源多个表时,可能会使用到union all把不同的表中计算的指标合起来。关于union all使用条件:两个要联合的SQL语句 字段个数必须一样,而且字段类型要“相容”(一致) 另外,回顾union和uni…...

【⑰MySQL】 变量 | 循环 | 游标 | 处理程序
前言 ✨欢迎来到小K的MySQL专栏,本节将为大家带来MySQL变量 | 循环 | 游标 | 处理程序的分享✨ 目录 前言1. 变量1.1系统变量1.2 用户变量 2. 定义条件与处理程序2.1 案例分析2.2 定义条件2.3 定义处理程序2.4 案例解决 3. 流程控制3.1 分支结构3.2 循环结构3.3 跳转…...
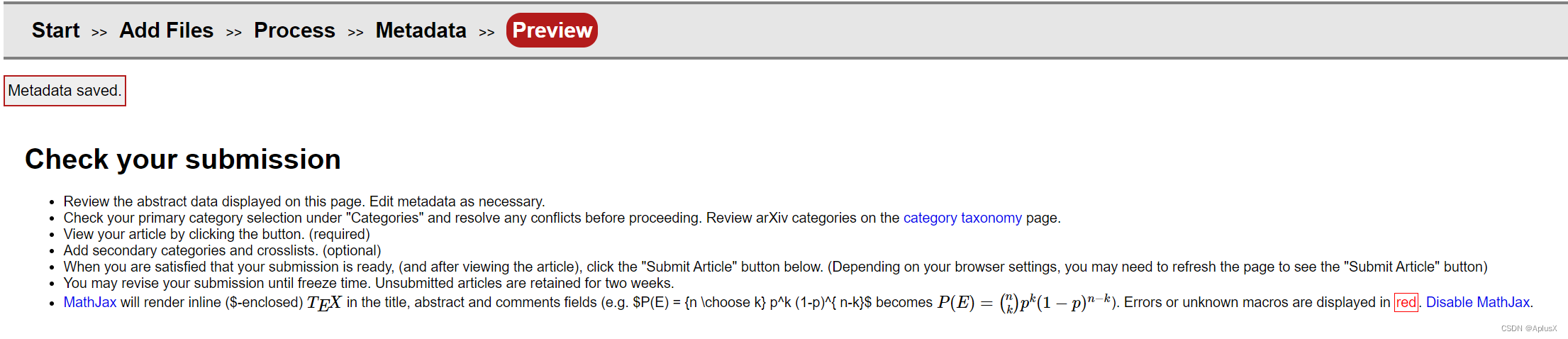
如何在arXiv上发表一篇文章
目录 1. 初始信息确认2. 提交论文文件3. 论文编译结果4. 补充论文信息5. 总览 1. 初始信息确认 版权问题需要根据个人情况选择。 IEEE, Elsevier, BioMed Central, 这几个出版商都允许在投稿之前挂文章到arXiv下。通常是选择: arXiv.org perpetual, non-exclusive l…...

重要性采样
重要性采样 前言 离散型随机变量 X X X,我们可以通过以下方法求取其期望: 直接计算法,需要知道概率分布: E ( X ) ∑ x ∈ X [ p ( x ) ⋅ x ] \mathbb{E}(X)\sum_{x\in X}\left[p(x)\cdot x\right] E(X)x∈X∑[p(x)⋅x] 采…...

说说Omega架构
分析&回答 Omega架构我们暂且称之为混合数仓。 什么是ECS设计模式 在谈我们的解法的时候,必须要先提ECS的设计模式。 简单的说,Entity、Component、System分别代表了三类模型。 实体(Entity):实体是一个普通的对象。通常,…...

高忆管理:光刻胶概念强势拉升,同益股份、格林达涨停
光刻胶概念5日盘中强势拉升,截至发稿,同益股份、格林达涨停,波长光电、晶瑞电材涨超7%,容大感光涨逾5%,华懋科技、茂莱光学、苏大维格、南大光电等均走强。 音讯面上,据新加坡《联合早报》网站9月2日报导&…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...
