数学建模:线性与非线性优化算法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛
数学建模:线性与非线性优化算法
优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值
优化的两个关键点:
1.明确优化的目标函数
2.明确优化变量之间需要满足的约束
线性优化
使用函数:linprog
函数原型:
[x,fval]=linprog(f,A,b,Aeq,Beq,LB,UB)
- x:求得最优情况下变量的解
- fval:求得最优目标值
- f:目标函数的系数(符号按最小值标准,若目标是求解机大值可以通过添加负号改成求极小值)
- A:不等式约束的变量系数(符合按小于标准,如果是大于约束可通过加负号变成小于)
- b:不等式约束的常量
- Aeq:等式约束的变量系数
- Beq:等式约束的常量
- LB:变量的下限
- UB:变量的上限
例如我们需要计算求解如下线性函数的最优解:
m i n { − x 1 − 2 x 2 + 3 x 3 } x 1 + x 2 ⩾ 3 x 2 + x 3 ⩾ 3 x 1 + x 3 = 4 0 ≤ x 1 , x 2 , x 3 ≤ 2 \begin{gathered}min\{-x_1-2x_2+3x_3\} \\x_1+x_2\geqslant3 \\x_2+x_3\geqslant3 \\x_1+x_3=4 \\0\leq x_1,x_2,x_3\leq2 \end{gathered} min{−x1−2x2+3x3}x1+x2⩾3x2+x3⩾3x1+x3=40≤x1,x2,x3≤2
clc;clear;f = [-1;-2;3];
%% 不等式约束
A = [-1,-1,0;0,-1,-1];
B = [-3,-3];%% 等式约束
Aeq = [1,0,1];
Beq = [4];%% 上下限
LB = zeros(3,1);
UB = 2*ones(3,1);%% 线性优化
[x,fval] = linprog(f,A,B,Aeq,Beq,LB,UB);%% 输出结果objstr = ['目标函数最优值:',num2str(fval)];
disp(objstr);
for i = 1:length(x)xstr = ['x',num2str(i),'的系数为: ',num2str(x(i))];disp(xstr);
end
非线性优化
fmincon是MATLAB的非线性规划求解函数
[x,fval]=fmincon(fun,x0,A,b,Aeq,Beq,LB,UB,nonlcon)
- x:求得最优情况下变量的解
- fval:求得最优目标值
- fun:目标函数(符号按最小值标准,若目标是求解机大值可以通过添加负号改成求极小值)
- x0:初始解
- A:不等式约束的变量系数(符合按小于标准,如果是大于约束可通过加负号变成小于)
- b:不等式约束的常量
- Aeq:等式约束的变量系数
- Beq:等式约束的常量
- LB:变量的下限
- UB:变量的上限
- nonlcon :非线性约束函数表达式
m a x { x 1 2 − x 2 2 + x 2 x 3 } 2 x 1 + x 2 + 3 x 3 ≤ 6 x 1 2 + x 1 x 2 + x 2 x 3 ≤ x 2 + 6 0 ≤ x 1 , x 2 , x 3 ≤ 1 \begin{gathered}max\begin{Bmatrix}x_1^2-x_2^2+x_2x_3\end{Bmatrix} \\2x_1+x_2+3x_3\leq6 \\x_1^2+x_1x_2+x_2x_3\leq x_2+6 \\0\leq x_1,x_2,x_3\leq1 \end{gathered} max{x12−x22+x2x3}2x1+x2+3x3≤6x12+x1x2+x2x3≤x2+60≤x1,x2,x3≤1
clc;clear;% 指定初始解
x0 = zeros(3,1);
%% <线性>不等约束
A = [2,1,3];
B = [6];%% <线性>等式约束
Aeq = [];
Beq = [];%% 变量上下限
LB = zeros(3,1);
UB = 1*ones(3,1);%% 整体非线性优化目标函数
fun = @(x) -x(1)^2-x(2)^2+x(2)*x(3);%% 取得非线性不等式约束函数
nonlcon = @noLinearLimited;
[x,fval] = fmincon(fun,x0,A,B,Aeq,Beq,LB,UB,nonlcon);objstr=['目标函数最优值:',num2str(-fval)];
disp(objstr)
for i=1:length(x)xstr=['x',num2str(i),'的值为:',num2str(x(i))];disp(xstr)
end%% 非线性不等式约束的表达式,如果有多个,则在C后面加; 补充即可
function [C,Ceq] = noLinearLimited(x)C = [x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6];Ceq = [];
end
相关文章:

数学建模:线性与非线性优化算法
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:线性与非线性优化算法 优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小…...
数学建模--粒子群算法(PSO)的Python实现
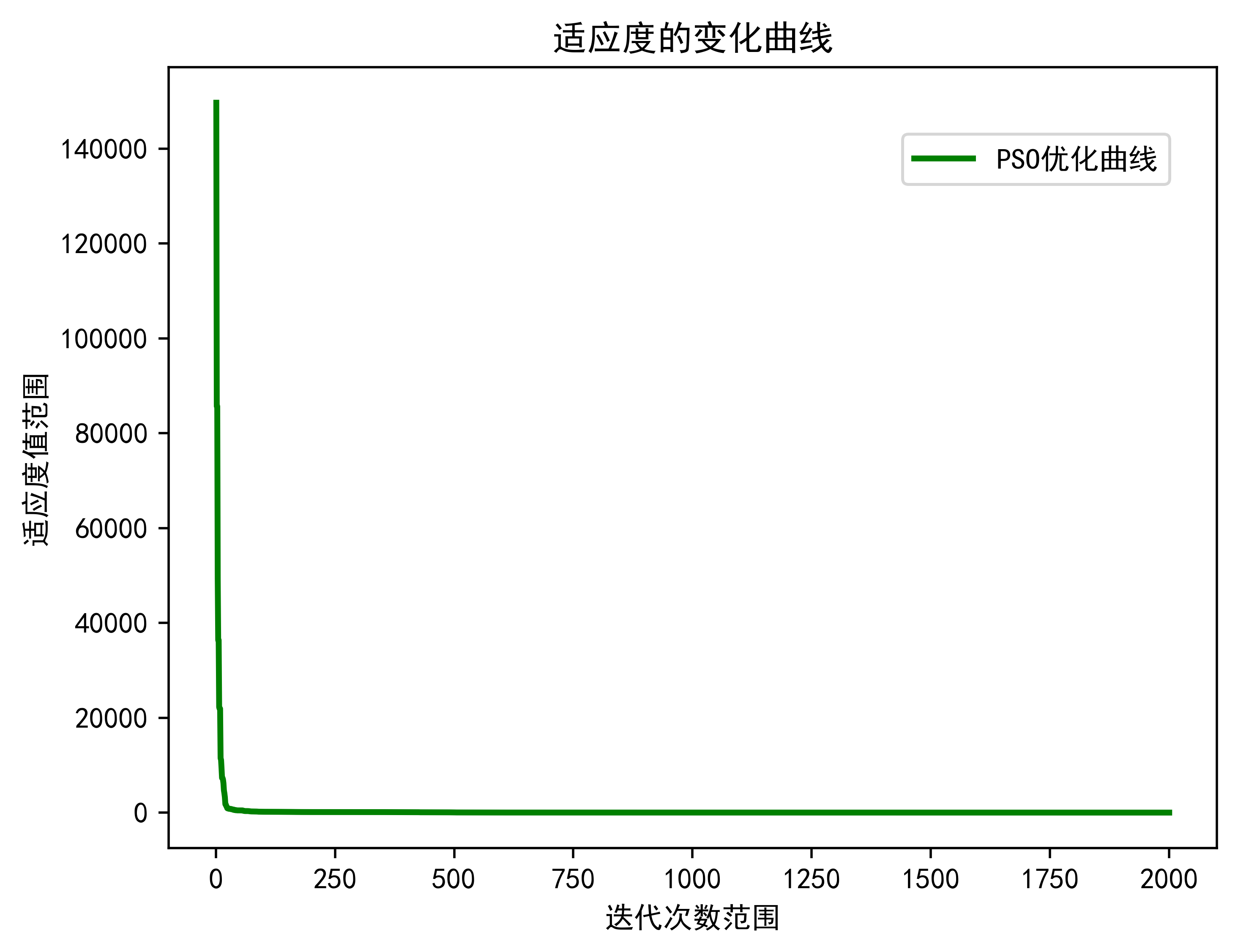
目录 1.开篇提示 2.算法流程简介 3.算法核心代码 4.算法效果展示 1.开篇提示 """ 开篇提示: 这篇文章是一篇学习文章,思路和参考来自:https://blog.csdn.net/weixin_42051846/article/details/128673427?utm_mediumdistribute.pc_relevant.none-task-blog-…...
【C++】STL-函数对象-内建函数对象
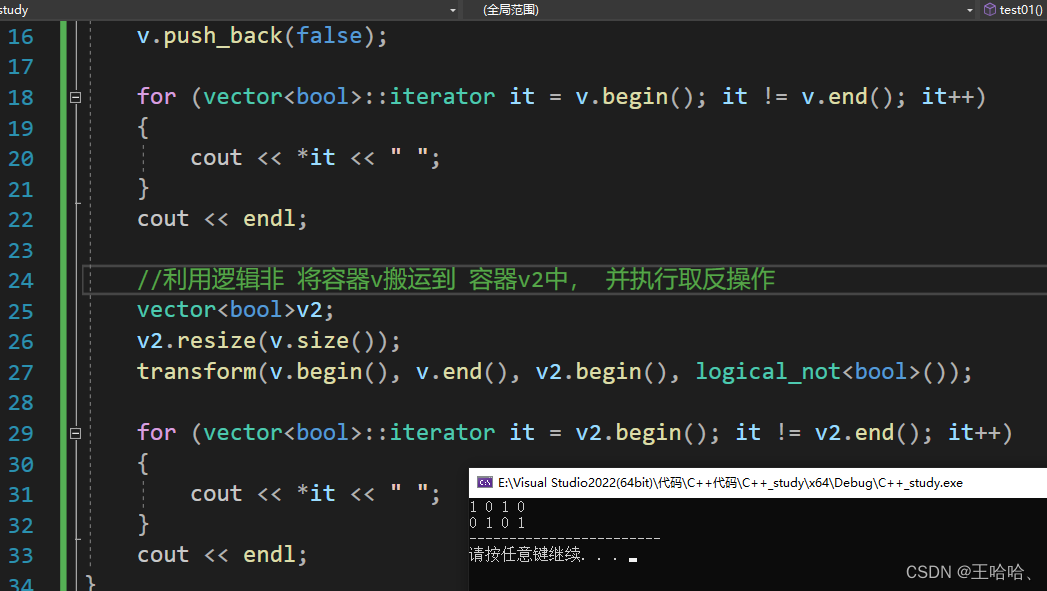
0.前言 1.算术仿函数 #include <iostream> using namespace std;// STL-内建函数对象-算术仿函数 #include<functional> // 内建函数对象头文件//以下举例两个仿函数 -- negate and plus// negate 一元仿函数 取反仿函数 void test01() {negate<int>n;cout …...

Redis 教程 - Redis 基本操作
Redis 教程 - Redis 基本操作 Redis(Remote Dictionary Server)是一个开源的内存数据库,它提供了键值对存储和多种数据结构的支持,被广泛应用于缓存、消息队列、计数器等场景。本教程将介绍 Redis 的基本操作,包括连接…...
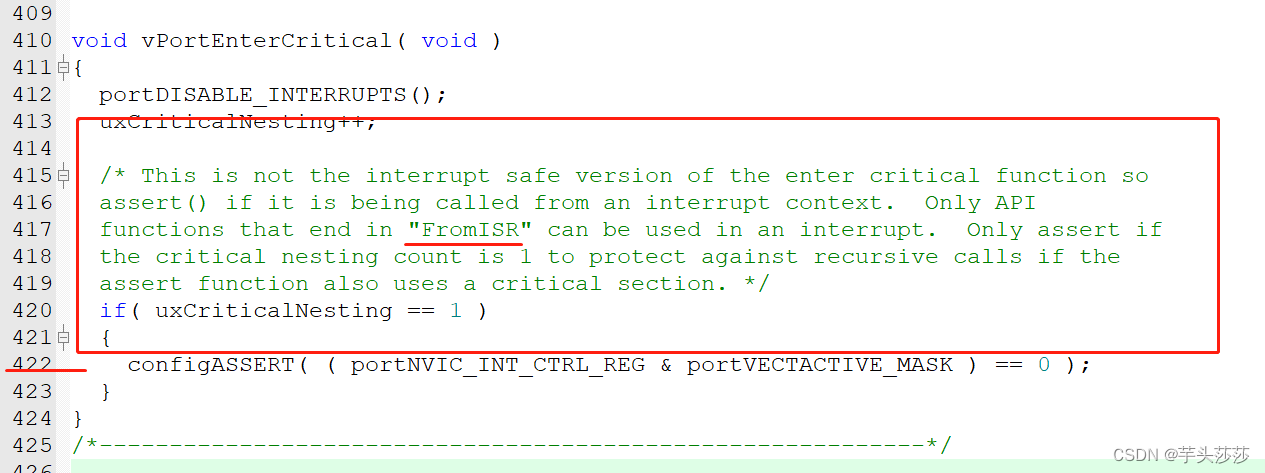
FreeRTOS中断与任务之间同步(Error:..\..\FreeRTOS\portable\RVDS\ARM_CM4F\port.c,422 )
前言: FreeRTOS中,中断需要注意几点: 何时使用中断;中断服务函数(ISR)要处理的数据量有多大,通常我们希望中断的切换越快越好,也就是说,ISR尽量采用耗时较少的处理方式…...

WebRTC清晰度和流畅度
WebRTC清晰度和流畅度 flyfish WebRTC提供了4种模式DISABLED,MAINTAIN_FRAMERATE,MAINTAIN_RESOLUTION,BALANCED // Based on the spec in // https://w3c.github.io/webrtc-pc/#idl-def-rtcdegradationpreference. // These options are …...

华为数通方向HCIP-DataCom H12-821题库(单选题:181-200)
第181题 某管理员需要创建AS Path过滤器(ip as-path-iter),允许AS_Path中包含65001的路由通过,那么以下哪一项配置是正确的? A、ip as-path-filter 1 permit 65001 B、ip as-path-filter 1 permit "65001 C、ip as-path-filter 1 permit *6500…...

海康威视二次开发适配安卓电视盒子
收到一个需求,需要在安卓电视盒子上适配海康威视摄像头视频: 1.类似电视家app界面,左边滑动菜单显示通道列表、设置按钮,遥控器呼出菜单。 2.遥控器操作:切换视频通道、云台上下左右控制、缩放等。 3.服务器域名、用…...

NIO原理浅析(二)
IO分类 阻塞和非阻塞 阻塞IO:用户空间引发内核空间的系统调用,需要内核IO操作彻底完成之后,返回值才会返回到用户空间,执行用户的操作。阻塞指的用户空间程序的执行状态,用户空间程序需要等到IO操作彻底执行完毕。j…...

leetcode每日一练-第53题-最大子数组和
一、思路 动态规划 二、解题方法 使用了两个变量 maxSum 和 currentSum 来分别记录全局的最大和和当前连续子数组的和。遍历数组时,我们不断更新 currentSum,并比较是否需要更新 maxSum。最后,maxSum 就是最大的连续子数组和。 三、code …...

京东云接入【风险识别】接口
京东云的接入文档写的真的跟逗你玩一样,就给提供了一个简单的实例,其他的全靠自己摸索。 这篇文章描述的是激动云【风险识别接口】接入,也会介绍如何接入其他的一些未在文章内描述到的接口。 这里使用的是python SDK,先安装 pip…...
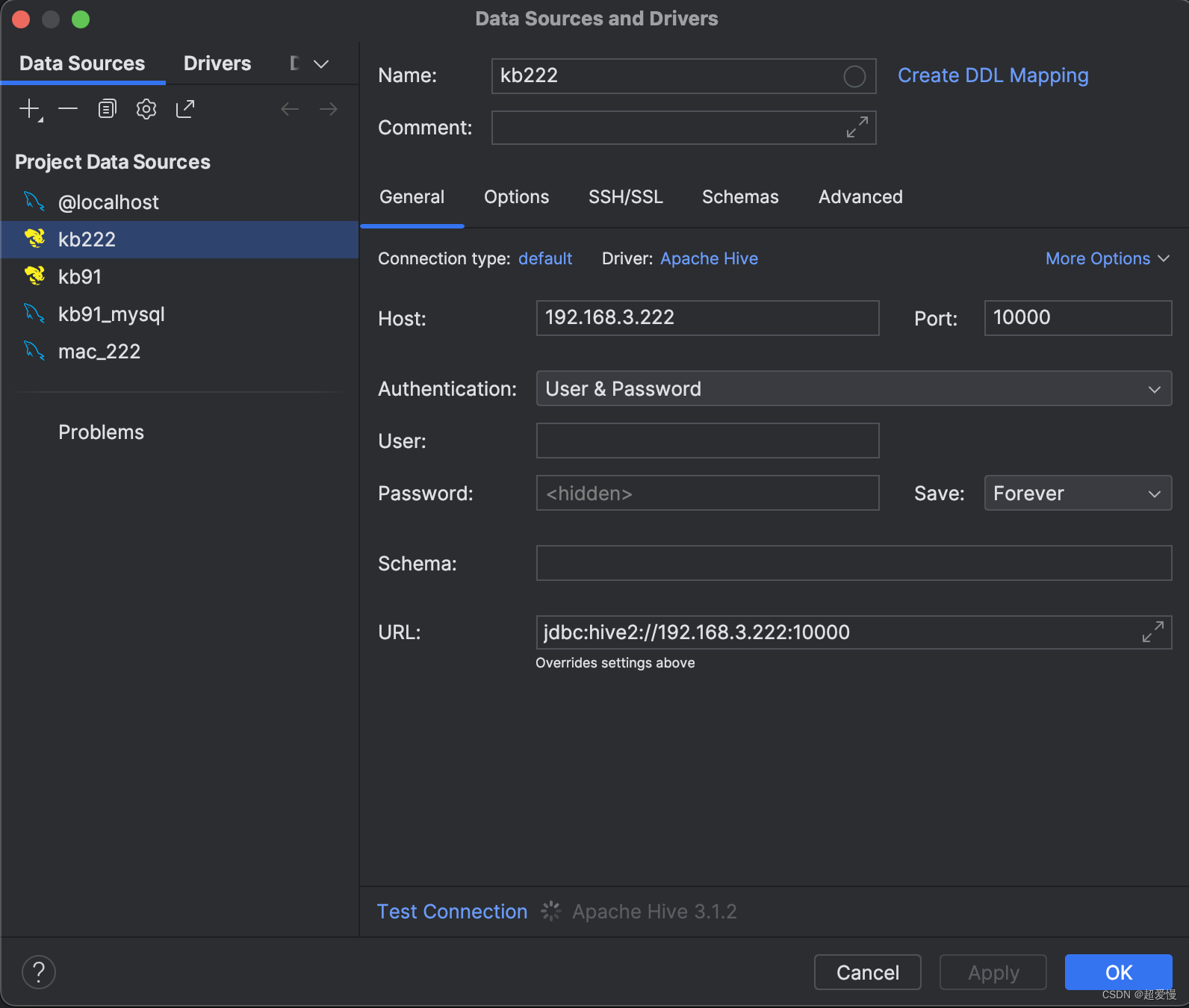
在 linux 虚拟机上安装配置 hive
目录 一 下载hive 安装包 二 解压 hive 并配置环境变量 三 配置hive 的配置文件 四 更新 guava 五 hive初始化 六 开启远程连接 七 使用datagrip 连接 hive 一 下载hive 安装包 百度网盘资源如下: 链接: https://pan.baidu.com/s/18jF-Qri0hc52_rtL61O0YQ?…...

作品集(陆续上传中)
智能家居---不断完善中 家居-CSDN直播 家居 语音刷抖音 --- 基于串口和adb 基于守护进程的语音刷抖音-CSDN直播 基于守护进程的语音刷抖音 海天一色项目 --- 船舶靠港零碳排加热器 FTP云盘 --- 多进程和socket FTP云盘-CSDN直播 FTP云盘...
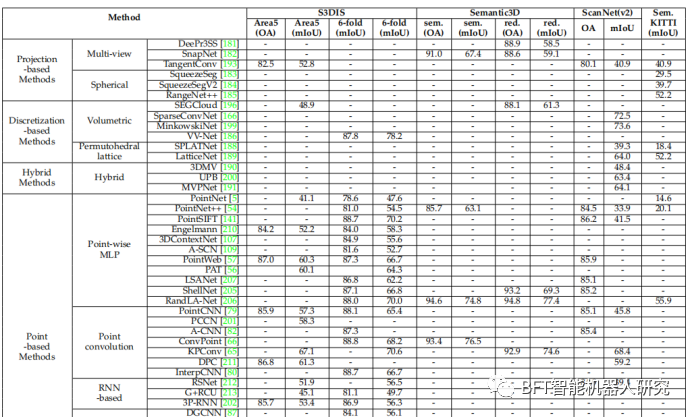
论文解读 | 三维点云深度学习的综述
原创 | 文 BFT机器人 KITTI 是作为基准测试是自动驾驶中最具影响力的数据集之一,在学术界和工业界都被广泛使用。现有的三维对象检测器存在着两个限制。第一是现有方法的远程检测能力相对较差。其次,如何充分利用图像中的纹理信息仍然是一个开放性的问题…...

基于costas环的载波同步系统matlab性能仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 ............................................................................ I_Dataroun…...

解码自我注意的魔力:深入了解其直觉和机制
一、说明 自我注意机制是现代机器学习模型中的关键组成部分,尤其是在处理顺序数据时。这篇博文旨在提供这种机制的详细概述,解释它是如何工作的,它的优点,以及它背后的数学原理。我们还将讨论它在变压器模型中的实现和多头注意力的…...

mysql之存储引擎
目录 存储引擎概念 MyISAM MyISAM特点 MyISAM 表的存储格式 MyISAM适用的生产场景 InnoDB InnoDB特点 选择存储引擎依据 MyISAM 和 INNODB区别 命令 查看系统支持的存储引擎 查看表使用的存储引擎 修改存储引擎 存储引擎概念 MySQL中的数据用各种不同的技术存…...
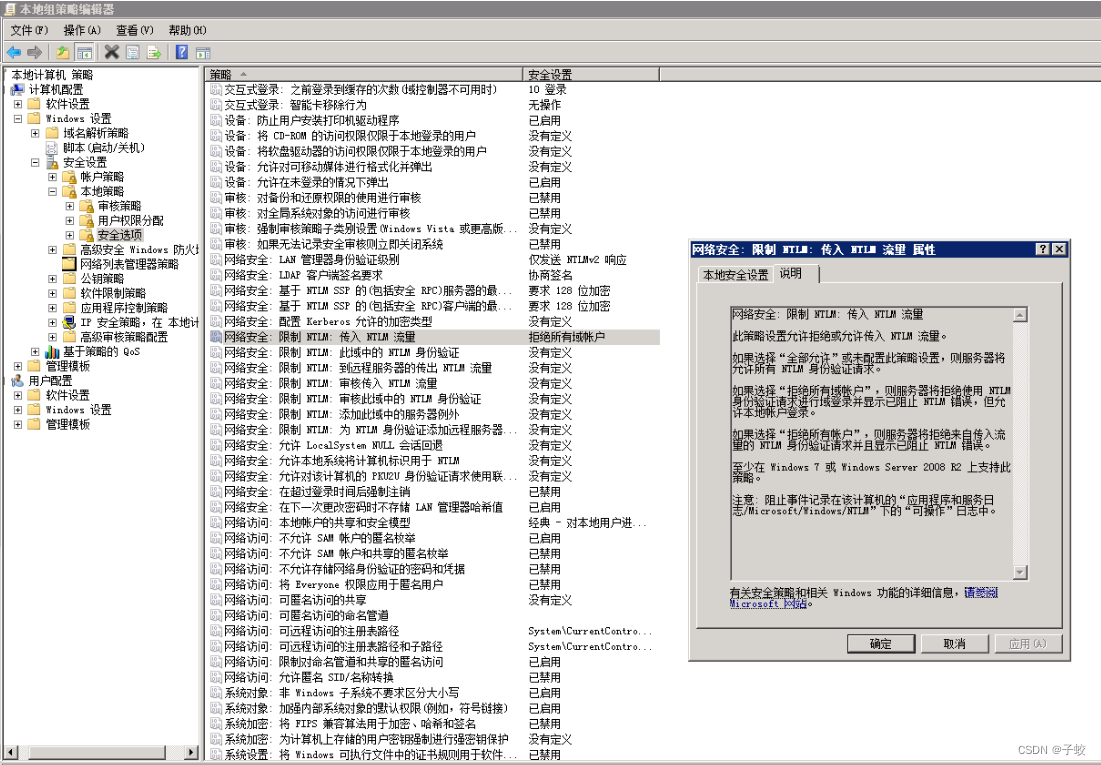
服务器日志出现大量NTLM(NT LAN Manager)攻击
日志名称:Security 来源: Microsoft-Windows-Security-Auditing 日期: 2023/8/30 20:57:40 事件 ID:4625 任务类别:登录 级别: 信息 关键字: 审核失败 用户: 暂缺 计算机: WIN-QBJ3ORTR0CF 描述: 帐户登录失败。 主题: 安全 ID:NULL SID 帐户名:- 帐户域:- …...
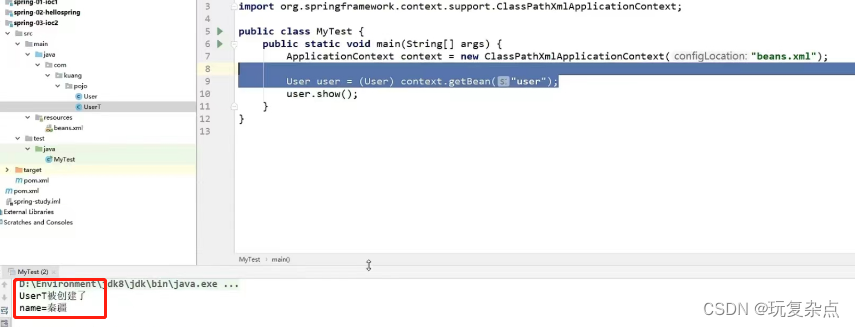
Spring学习|Spring简介、IOC控制反转理解、IOC创建对象方式
Spring Spring:春天------>给软件行业带来了春天! 2002,首次推出了Spring框架的雏形: interface21框架! Spring框架即以interface21框架为基础,经过重新设计,并不断丰富其内涵,于2004年3月24日发布了1.0正式版。 RodJohnson,Spring Framework创始人&…...
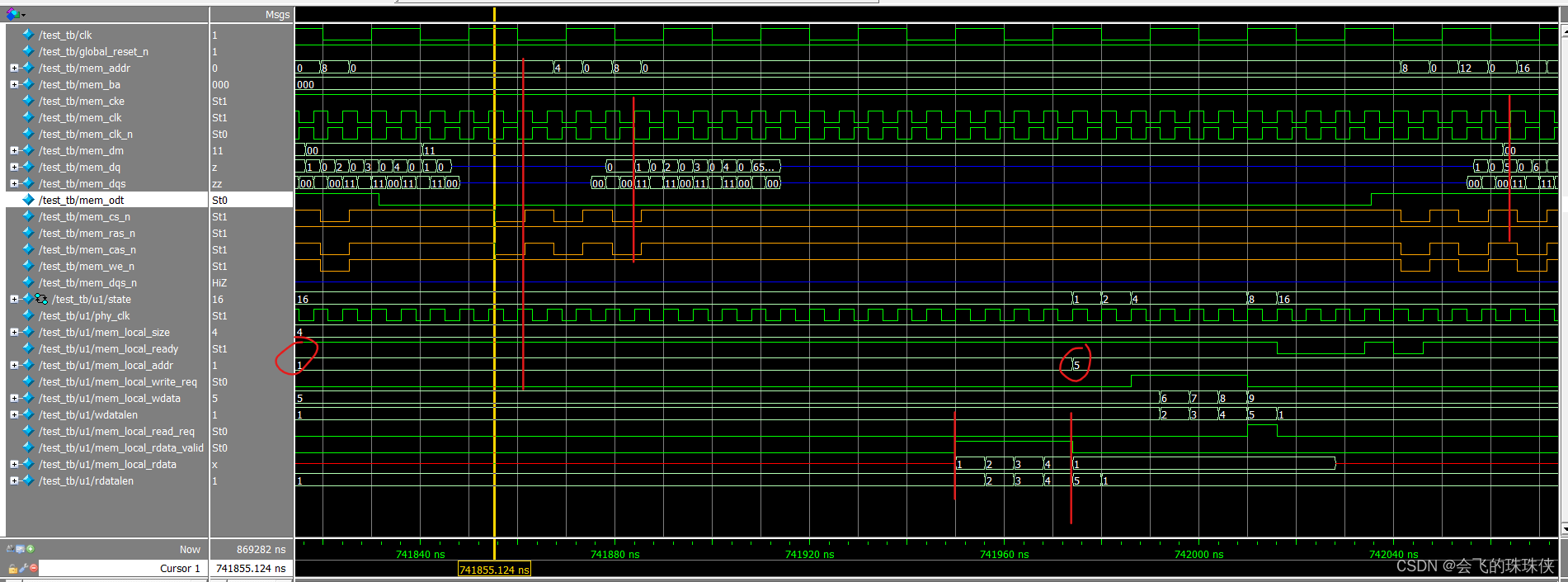
DDR2 IP核调式记录2
本文相对简单,只供自己看看就行。从其它的博客找了个代码,然后记录下仿真波形。 1. 功能 直接使用quartus生成的DDR2 IP核,然后实现循环 -->写入burst长度的数据后读出。 代码数据的传输是32位,实际使用了两片IC。因此IP核也是…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
