《热题101》动态规划篇
思路:需要一个二维数组dp来记录当前的公共子序列长度,如果当前的两个值等,则dp[i][j]=dp[i-1][j-1]+1,否则dp[i][j] = max(dp[i-1][j],dp[i][j-1])。也就是说,当前的dp值是由左、上、左上的值决定的。获得dp数组之后,倒序遍历这个二维数组,如果当前值和左边值相等,那就往左走,如果和上边值相等,就往上走,和左上值相等,就往左上走。并且保存当前的元素到ans中。最后将ans倒序输出。
class Solution:
def LCS(self , s1: str, s2: str) -> str:
n = len(s1)
m = len(s2)
if n <= 0 or m <= 0:
return '-1'
dp = [[0]*(m+1) for _ in range(n+1)]
ans = []
for i in range(n): #获取dp
for j in range(m):
if s1[i] == s2[j]:
dp[i+1][j+1] = dp[i][j]+1
else:
dp[i+1][j+1] = max(dp[i+1][j],dp[i][j+1])
a,b = n,m
while dp[a][b] != 0: #倒序遍历dp,取元素
if dp[a][b-1] == dp[a][b]: #该元素是从左边过来的
b -= 1
elif dp[a-1][b] == dp[a][b]: #该元素是从右边过来的
a -= 1
elif dp[a-1][b-1]+1 == dp[a][b]: #该元素是从左上过来的
a -= 1
b -= 1
ans.append(s1[a])
return ''.join(ans[::-1]) if len(ans) != 0 else '-1'
思路:子串一定是连续的,所以只需要记录dp[i+1][j+1] = dp[i][j]+1,其余都是0,每次更新值都要记录当前的最大长度和当前的结束位置。最后直接输出s1[index+1-res,index+1]即可。
class Solution:
def LCS(self, str1: str, str2: str) -> str:
n = len(str1)
m = len(str2)
if n <= 0 or m <= 0:
return ''
dp = [[0] * (m + 1) for _ in range(n + 1)]
res = 0
index = 0
for i in range(n):
for j in range(m):
if str1[i] == str2[j]:
dp[i + 1][j + 1] = dp[i][j] + 1
if res < dp[i+1][j+1]:
res = dp[i+1][j+1]
index = i
return str1[index+1-res:index+1]
但是这个方法会超时,可以使用值遍历一次的方法,寻找一个index,使得s1[index-maxlen,index+1]在s2中,更新maxlen和res继续寻找。
class Solution:
def LCS(self , str1: str, str2: str) -> str:
#让str1为较长的字符串
if len(str1) < len(str2):
str1, str2 = str2, str1
res = ''
max_len = 0
#遍历str1的长度
for i in range(len(str1)):
if str1[i - max_len : i + 1] in str2: #查找是否存在
res = str1[i - max_len : i + 1]
max_len += 1
return res
思路:由于机器人只能往右或者往下走,所以一个格子的路径等于它上边+左边的路径数。第一个格子的路径置为1,计算dp。
class Solution:
def uniquePaths(self , m: int, n: int) -> int:
if n <= 1 or m <= 1:
return 1
dp = [[0]*(n+1) for _ in range(m+1)]
dp[1][1] = 1
for i in range(1,m+1):
for j in range(1,n+1):
if i == 1 and j == 1:
continue
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[-1][-1]
思路:从左上角走,只能向右或者向下走,对于第一列的格子,最小值一定是上面的权重加上当前权重,对于第一行的格子,最小值是左边的权重加上当前的权重。其他格子是左边或者上边的最小值加上当前权重。用dp保存每个格子的最小值,输出dp的最后一个值。
class Solution:
def minPathSum(self , matrix: List[List[int]]) -> int:
n = len(matrix)
m = len(matrix[0])
if n <= 0 or m <= 0:
return 0
dp = [[0]*(m) for _ in range(n)]
dp[0][0] = matrix[0][0]
for i in range(n):
for j in range(m):
if i == 0 and j == 0:
continue
elif i == 0 and j != 0: #第一行
dp[i][j] = dp[i][j-1] + matrix[i][j]
elif i != 0 and j == 0: #第一列
dp[i][j] = dp[i-1][j] + matrix[i][j]
elif i-1 >= 0 and j - 1 >= 0: #其他格子
dp[i][j] = min(dp[i][j-1]+matrix[i][j],dp[i-1][j]+matrix[i][j])
return dp[-1][-1]
思路:首先要判断字符串不能有前导0,不能为0。然后遍历传入的字符串(1,n),对当前字符串进行分类,如果是0,i-1是[1,2]说明该位置只能一种编码dp[i+1]=dp[i],如果是其他字符,就直接返回0。当前值是[1-6],如果i-1是[1,2],那该位置是两种编码dp[i+1]=dp[i]+dp[i-1],其他字符就是只有一种编码。当前值是[7-9],如果i-1是1,有两种编码,其他字符一种编码。
class Solution:
def solve(self , nums: str) -> int:
n = len(nums)
if n <= 0:
return 0
#判断前导0和值为0
if len(str(int(nums))) != len(nums) or int(nums) == 0: return 0
dp = [1]*(n+1)
for i in range(1,n):
if nums[i] == '0': #当前是0
if nums[i-1] in ['1','2']: dp[i+1] = dp[i] #合法情况一种编码
else: return 0 #其他返0
elif '1' <= nums[i] <= '6': #当前是1-6
if nums[i-1] in ['1','2']: dp[i+1] = dp[i-1] + dp[i] #两种编码
else: dp[i+1] = dp[i] #一种编码
elif '7' <= nums[i] <='9': #当前是7-9
if nums[i-1] == '1': dp[i+1] = dp[i] + dp[i-1] #两种编码
else: dp[i+1] = dp[i] #一种编码
return dp[-1]
思路:dp[i]为凑出i元需要的最少货币数,想要凑出aim元,最多需要aim个货币。dp的初始值为aim+1(该值不可能被取到)。遍历[1-aim]的钱数,再遍历arr中的面值,当前面值小于等于钱数才能使用该面值。dp[i]=min(dp[i],dp[i-j]+1)。最后输出dp[-1]如果该值小于等于aim,说明该值被是合法值。否则说明凑不出这个钱,返回-1.
class Solution:
def minMoney(self , arr: List[int], aim: int) -> int:
#特殊情况判断
if len(arr) <= 0 and aim > 0: return -1
if aim == 0: return 0
if aim < min(arr): return -1
#设置dp,dp[i]表示达i元需要dp[i]的货币数
dp = [aim+1 for _ in range(aim+1)]
dp[0] = 0
#遍历钱数
for i in range(1,aim+1):
#遍历面值
for j in arr:
if j <= i: #当面值小于等于i元才能用该面值
dp[i] = min(dp[i],dp[i-j]+1)
return dp[-1] if dp[-1] <= aim else -1 #对最后的值判断再输出
思路:遍历两次数组,对于 i 的前面的数 j ,如果num[j]<num[i],就更新dp的值。dp[i] = max(dp[i],dp[j]+1),并且更新此时的ans,ans = max(ans,dp[i])
class Solution:
def LIS(self , arr: List[int]) -> int:
if len(arr) <= 1:
return len(arr)
dp = [1]*len(arr)
ans = 0
for i in range(len(arr)):
for j in range(i):
if arr[j] < arr[i]:
dp[i] = max(dp[i],dp[j]+1)
ans = max(ans,dp[i])
return ans
思路:当前的最大和,要么是前面的和+当前值,要么是当前值。dp[i] = max(array[i],dp[i-1]+array[i]),最后输出max(dp)。
class Solution:
def FindGreatestSumOfSubArray(self , array: List[int]) -> int:
if len(array) <= 1:
return array[0]
dp = []
dp.append(array[0])
for i in range(1,len(array)):
dp.append(max(array[i],dp[i-1]+array[i]))
return max(dp)
思路:回文子串有两种可能:bab,或者baab,也就是从一个字符串往两边延伸,可能获得一个回文串,或者用两个字符串往两边延伸也可能获得回文串。遍历每个字符,计算两种可能的回文串长度,并且和当前答案比较,如果大,就更新答案。
class Solution:
def length(self,A,left,right):
while left >= 0 and right < len(A) and A[left] == A[right]: #符合回文串
left -= 1
right += 1
return right -1 - left #(right-1)-(left+1)+1,当前回文串长度
def getLongestPalindrome(self , A: str) -> int:
if len(A) <= 1:
return len(A)
ans = 0
for i in range(len(A)):
ans = max(ans,self.length(A,i,i),self.length(A,i,i+1))
return ans
思路:循环分割,每次判断前导0和255大小。
class Solution:
def restoreIpAddresses(self , s: str) -> List[str]:
if len(s) == 0:
return []
ans = []
for i in range(1,len(s)-2):
for j in range(i+1,len(s)-1):
for k in range(j+1,len(s)):
a,b,c,d = s[:i],s[i:j],s[j:k],s[k:]
if len(str(int(a))) != len(a) or len(str(int(b))) != len(b) or len(str(int(c))) != len(c) or len(str(int(d))) != len(d): #前导0
continue
elif int(a) > 255 or int(b) > 255 or int(c) > 255 or int(d) > 255 : #判断和255大小
continue
else:
ans.append('.'.join([a,b,c,d]))
return ans
思路:dp[i]=max(dp[i-1],dp[i-2]+nums[i])
class Solution:
def rob(self , nums: List[int]) -> int:
n = len(nums)
dp = [0]*n
for i in range(n):
if i == 0:
dp[i] = nums[i]
elif i == 1:
dp[i] = max(nums[i-1],nums[i])
elif i >= 2:
dp[i] = max(dp[i-1],dp[i-2]+nums[i])
return dp[-1]
思路:和前一个题的思路,不同之处在于环,所以有两种情况:
第一家偷了,就不能偷最后一家,最大值是倒数第二家的最大值;
第一家不偷,可以投最后一家,最大值是倒数第一家的最大值。
class Solution:
def rob(self , nums: List[int]) -> int:
n = len(nums)
#环形的主要区别是,偷第一家就不偷最后一家,偷最后一家就不偷第一家
dp1 = [0]*n
dp2 = [0]*n
#一定偷第一家
dp1[0] = nums[0]
for i in range(1,n):
if i == 1:
dp1[i] = dp1[i-1]
else:
dp1[i] = max(dp1[i-2]+nums[i],dp1[i-1])
#一定偷最后一家
dp2[0] = 0
for i in range(1,n):
if i == 1:
dp2[i] = nums[i]
else:
dp2[i] = max(dp2[i-2]+nums[i],dp2[i-1])
return max(dp1[-2],dp2[-1]) #dp1最后一家不能偷,所以只能拿倒数第二家的最大值
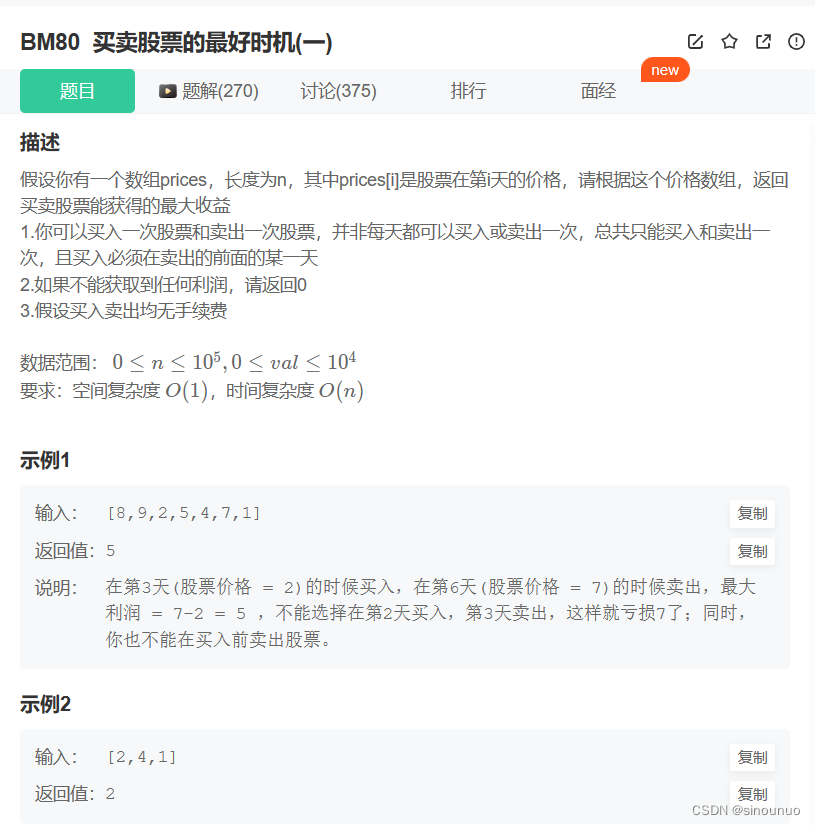
思路:只能买卖一次的情况下,如果当前是i,选择[0-i]的最小值,[i:len-1]的最大值,ans表示两者之差,如果差值变大就更新ans。
class Solution:
def maxProfit(self , prices: List[int]) -> int:
ans = 0
for i in range(len(prices)):
a = min(prices[:i+1]) #[0,i]
b = max(prices[i:]) #[i,len-1]
ans = max(ans,b-a)
return ans
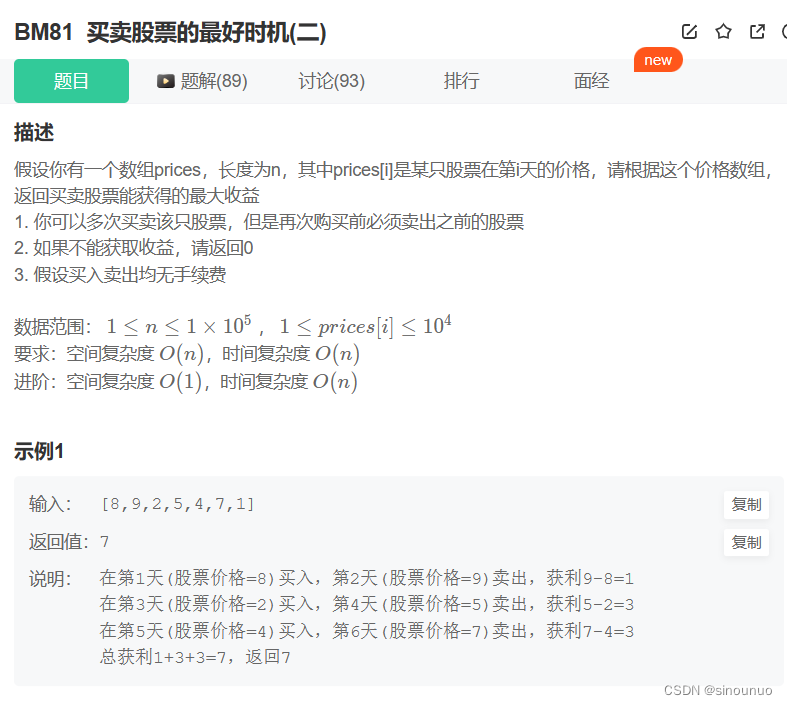
思路:可以有多次买卖股票的情况下,当前是第i天,在当前能够得到的最大获利分为两种情况,第一种是今天持有股票:dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])要么前一天也持有,今天就不变,要么前一天不持有,今天就购买。第二种是今天不持有股票,要么前一天也不持有,今天不变,要么前一天持有,今天卖出。dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i]),返回最后一天不持有的数值。
class Solution:
def maxProfit(self , prices: List[int]) -> int:
n = len(prices)
if n <= 1:
return 0
dp = [[0,0] for _ in range(n)]
for i in range(len(prices)):
if i == 0:
dp[i][0] = 0
dp[i][1] = -prices[i]
else:
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])
return dp[-1][0]
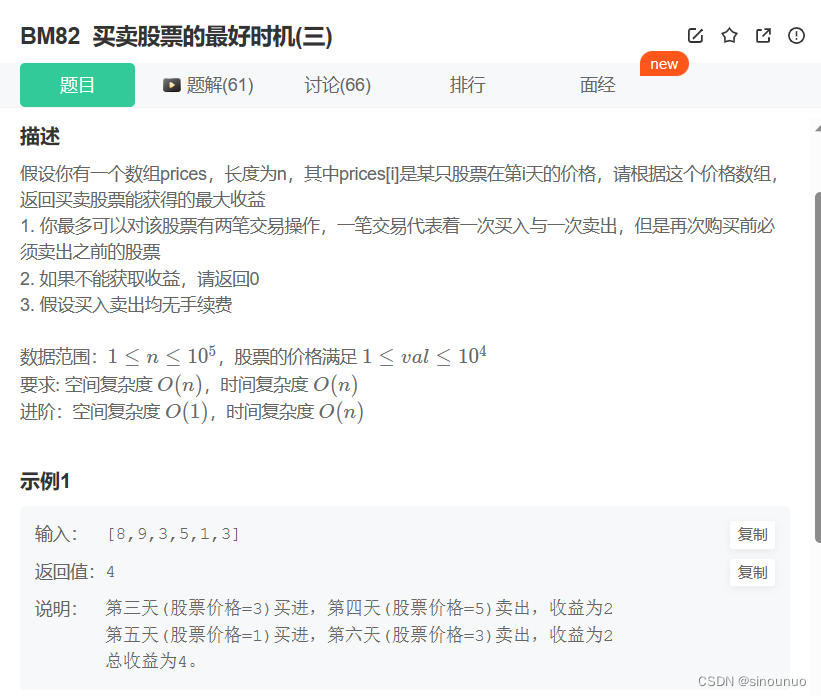
思路:因为只能买两次,所以本次状态转移就有五个选择
- dp[i][0]表示到第i天为止没有买过股票的最大收益
- dp[i][1]表示到第i天为止买过一次股票还没有卖出的最大收益
- dp[i][2]表示到第i天为止买过一次也卖出过一次股票的最大收益
- dp[i][3]表示到第i天为止买过两次只卖出过一次股票的最大收益
- dp[i][4]表示到第i天为止买过两次同时也买出过两次股票的最大收益
class Solution:
def maxProfit(self , prices: List[int]) -> int:
n = len(prices)
if n <= 3:
return 0
dp = [[-10000]*5 for i in range(n)]
dp[0][0] = 0
dp[0][1] = -prices[0]
for i in range(1,n):
dp[i][0] = dp[i-1][0]
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])
dp[i][2] = max(dp[i-1][2],dp[i-1][1]+prices[i])
dp[i][3] = max(dp[i-1][3],dp[i-1][2]-prices[i])
dp[i][4] = max(dp[i-1][4],dp[i-1][3]+prices[i])
return dp[-1][4]
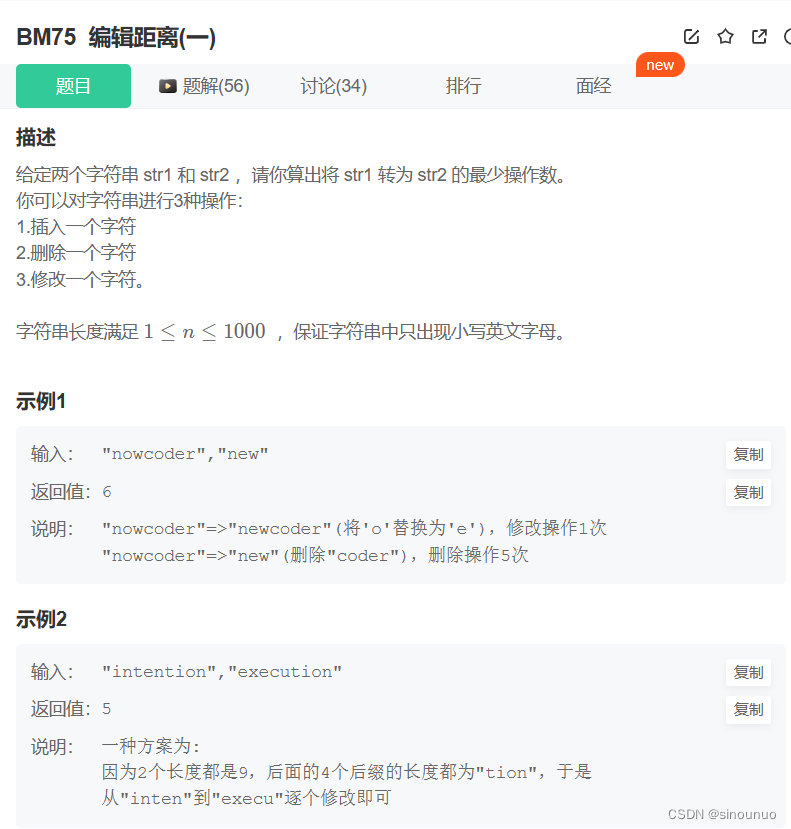
思路:两个字符串或者两个数组来确定相同子串或者改成相同,都按照二维dp思考,如果当前两个子串的对应位置不等,那该处的最小值是左、上、左上的最小值+1,如果等,就是左上对角线的值。
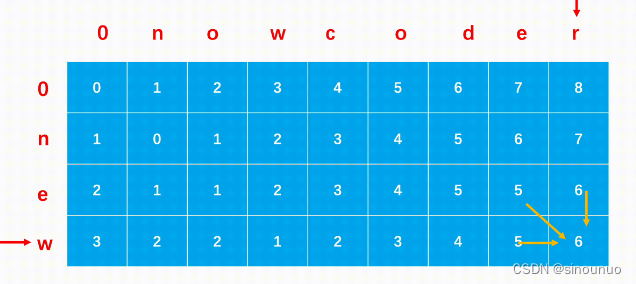
class Solution:
def editDistance(self , str1: str, str2: str) -> int:
n = len(str1)
m = len(str2)
dp = [[0]*(m+1) for _ in range(n+1)]
for i in range(n+1):
for j in range(m+1):
if i == 0:
dp[i][j] = j
elif j == 0:
dp[i][j] = i
else:
if str1[i-1] != str2[j-1]:
dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1
else:
dp[i][j] = dp[i-1][j-1]
return dp[-1][-1]
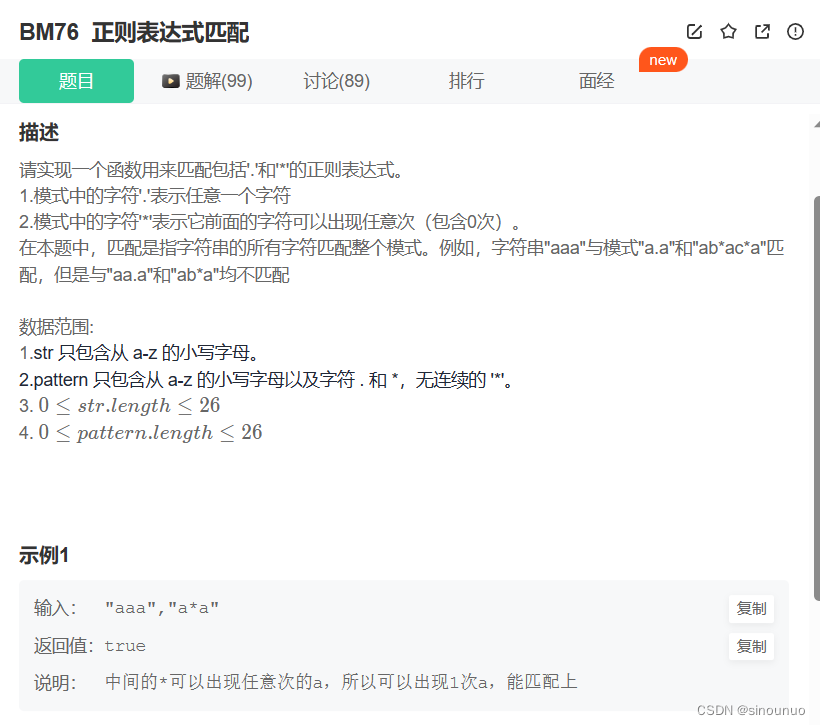
思路:首先进行长度异常判断,如果没有模式长度,那字符串长度也应该为空。然后开始匹配字符串和模式的第一位first_match。然后递归匹配之后的情况,如果第二位出现了*,那第一位不匹配也没有关系,匹配(s,pattern[2:]),如果第一位匹配,就匹配之后的(s[1:],pattern)。
如果第二位没有*,就递归first_match和(s[1:],pattern[1:])
class Solution:
def match(self , s: str, pattern: str) -> bool:
if not pattern : return not s
first_match = s and pattern[0] in [s[0],'.']
if len(pattern) >= 2 and pattern[1] == '*':
return self.match(s,pattern[2:]) or first_match and self.match(s[1:],pattern)
else:
return first_match and self.match(s[1:],pattern[1:])

思路:使用栈,让栈顶是当前没有匹配的括号的下标,保证栈不空,将-1先入栈。首先遇到'('就让左括号的下标入栈,如果遇到')',如果当前栈的长度大于1(已经有左括了),就弹出栈顶做匹配,res更新为max(res,i - stack[-1]);如果当前长度不大于1(没有左括号),就更新栈顶为当前没有匹配的右括号的下标(stack[-1] = i)
class Solution:
def longestValidParentheses(self , s: str) -> int:
stack = [-1]
res = 0
for i,ch in enumerate(s):
if ch == '(':
stack.append(i) #左括号下标入栈
else:
if len(stack) > 1:
stack.pop()
res = max(res,i - stack[-1])
else:
stack[-1] = i
return res
相关文章:

《热题101》动态规划篇
思路:需要一个二维数组dp来记录当前的公共子序列长度,如果当前的两个值等,则dp[i][j]dp[i-1][j-1]1,否则dp[i][j] max(dp[i-1][j],dp[i][j-1])。也就是说,当前的dp值是由左、上、左上的值决定的。获得dp数组之后,倒序…...

【综述+3D】基于NeRF的三维视觉2023年度进展报告(截止2023.06.10)
论文:2003.Representing Scenes as Neural Radiance Fields for View Synthesis 官方网站:https://www.matthewtancik.com/nerf 突破性后续改进: Instant Neural Graphics Primitives with a Multiresolution Hash Encoding | 展示官网&#…...

基于JavaScript粒子流动效果
这是一个HTML文件,主要包含了一些CSS样式和JavaScript代码,用于创建一个动画效果。 在CSS部分,定义了一些基本的样式,包括页面的背景颜色、位置、大小等。特别的,定义了两种球形元素(.ball_A 和 .ball_B&am…...
【U盘】实现U盘清空并重置恢复存储
打开电脑,将U盘插入USB端口,点按快捷键【WinR】,弹出运行对话框,输入命令 diskpart 进入命令提示符窗口 输入指令 list disk 查看现在的硬盘 这里显示的U盘编号是“1”,因此输入select disk “1”,就是选择…...
基于Hugo 搭建个人博客网站
目录 1.环境搭建 2.生成博客 3.设置主题 4.将博客部署到github上 1.环境搭建 1)安装Homebrew brew是一个在 macOS 操作系统上用于管理软件包的包管理器。类似于centos下的yum或者ubuntu下的apt,它允许用户通过命令行安装、更新和管理各种软件工具、…...
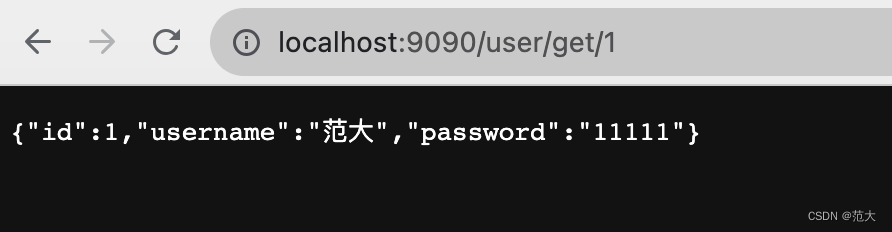
Springboot + Sqlite实战(离线部署成功)
最近有个需求,是手机软件离线使用, 用的springboot mybatis-plus mysql,无法实现,于是考虑使用内嵌式轻量级的数据库SQLlite 引入依赖 <dependency><groupId>org.xerial</groupId><artifactId>sqlite-…...
:MLWE 问题与NTT(附源码分析))
【后量子密码】CRYSTALS-KYBER 算法(一):MLWE 问题与NTT(附源码分析)
一、前言 大多数基于数论的密码学,如Diffie-Hellman协议和RSA加密系统,依赖于大整数因子分解或特定群的离散对数等困难问题。然而,Shor 在1997年给出了对所有这些问题的高效量子算法,这将使得基于数论的密码系统在未来量子计算机时代变得不安全。相比之下,目前对于格密码…...

VTK——angleWidget的3D转换
文章目录 3D空间坐标转换例程心得 3D空间坐标转换 在冠状图、矢状面、横截面等创建的角度组件的三个端点坐标,不能直接用在3D视图中。这是因为2D切片的坐标是基于像素的,而3D空间的坐标可能是基于实际物理尺寸的。 解决方案是使用2D点的坐标、切片的物理…...
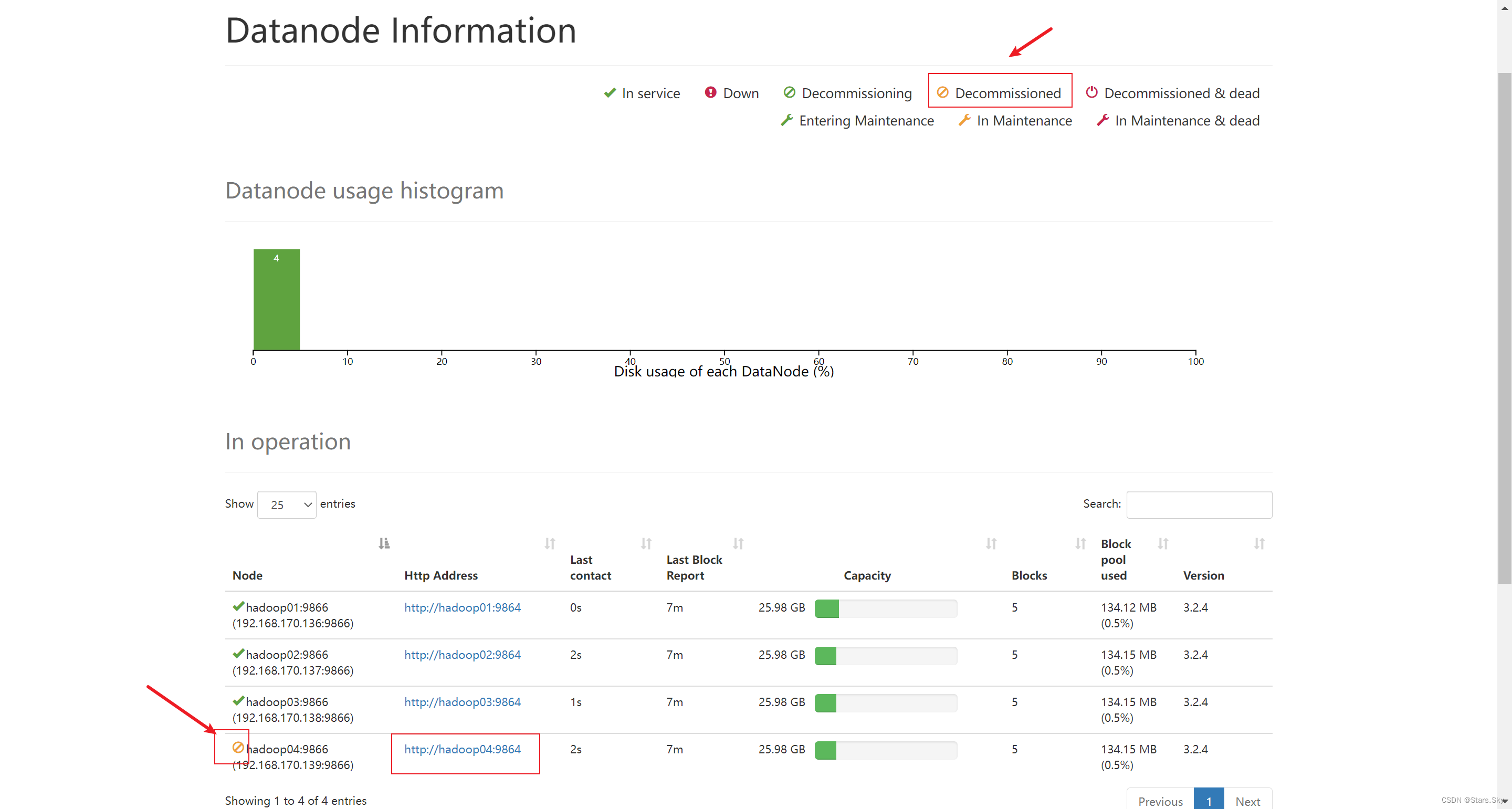
HDFS 集群动态节点管理
目录 一、动态扩容、节点上线 1.1 背景 1.2 扩容步骤 1.2.1 新机器基础环境准备 1.2.2 Hadoop 配置 1.2.3 手动启动 DataNode 进程 1.2.4 Web 页面查看情况 1.2.5 DataNode 负载均衡服务 二、动态缩容、节点下线 2.1 背景 2.2 缩容步骤 2.2.1 添加退役节点 …...
postman9.12.汉化版(附有下载链接)
想用英文版本的可以直接点击下载最新版本 这里直接付上9.12.2版本的下载链接,如果大家要下载别的版本,可以直接修改链接里面的版本号即可 ,下面是汉化包下载 链接:https://pan.baidu.com/s/1izK3HfqlfXJdq6KIYeJ2zw?pwdpetk 提…...
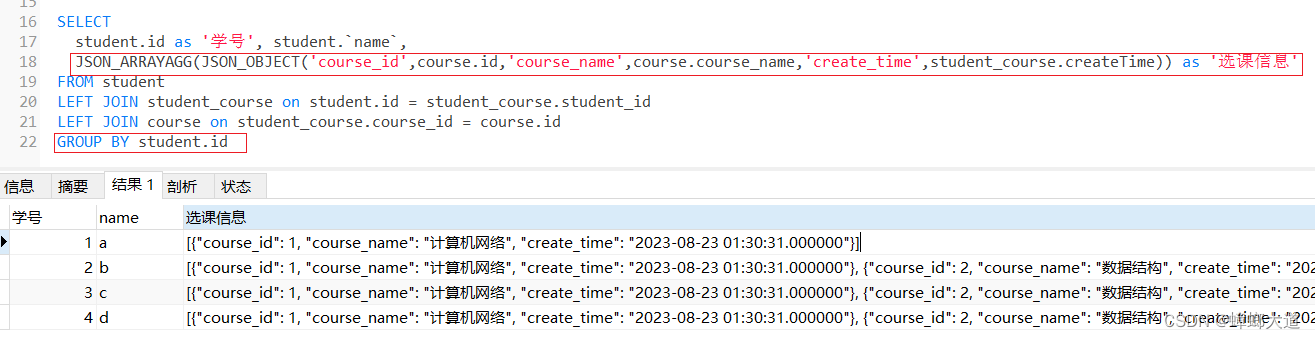
mysql与msql2数据驱动
mysql基本使用 数据库操作(DDL) -- 数据考操作 -- 1.查询所有数据库 SHOW DATABASES;-- 2.选择数据库 USE learn_mysql;-- 3.当前正在使用的数据库 SELECT DATABASE();-- 4.创建数据库 CREATE DATABASE IF NOT EXISTS learn_mysql;-- 5.删除数据库 DRO…...

解决微信小程序回调地狱问题
一、背景 小程序开发经常遇到根据网络请求结果,然后继续 处理下一步业务操作,代码如下: //1第一个请求 wx.request({url:"https://example.com/api/",data:data,success:function(res){//2第二个请求 wx.request({url:"http…...

cron介绍
cron表达式在线生成 在使用定时调度任务的时候,我们最常用的,就是cron表达式了。通过cron表达式来指定任务在某个时间点或者周期性的执行。 cron表达式的组成 cron表达式是一个字符串,由6到7个字段组成,用空格分隔。其中前6个字…...
mkp勒索病毒的介绍和防范,勒索病毒解密,数据恢复
mkp勒索病毒是一种新兴的电脑病毒,它会对感染的电脑进行加密,并要求用户支付一定的赎金才能解锁。这种病毒已经引起了全球范围内的关注,因为它不仅具有高危害性,而且还有很强的传播能力。本文将对mkp勒索病毒进行详细介绍…...

【面试精品】关于面试会遇到的Apache相关的面试题
1. Apache HTTP Server 基于什么协议提供网页浏览服务? 答:基于标准的http网络协议提供网页浏览服务。 2. 简述编译安装httpd软件包的基本过程? 答:解包,配置,编译,安装。 3. 编译安装httpd软…...

python对文件转md5,用于文件重复过滤
直接上代码 import hashlibdef calculate_md5(file_path):# 创建 MD5 哈希对象md5_hash hashlib.md5()# 打开文件并逐块读取,更新哈希值with open(file_path, rb) as file:while True:data file.read(8192) # 逐块读取文件,每块大小为 8192 字节if n…...

mac苹果电脑删除顽固残留软件图标
核心:删除“启动台”数据库里对应app的信息 1、打开访达(Finder),点击最顶部菜单栏的【前往》前往文件夹】,接着输入【/private/var/folders】 2、在弹出的访达(Finder)窗口搜索栏输入【com.ap…...

【jsvue】联合gtp仿写一个简单的vue框架,以此深度学习JavaScript
用 gtp 学习 Vue 生命周期的原理 lifecycle.js function Vue(options) {// 将选项保存到实例的 $options 属性中this.$options options;// 若存在 beforeCreate 钩子函数,则调用之if (typeof options.beforeCreate function) {options.beforeCreate.call(this);…...

linux centos7 系统之编程:求水仙花数
在Python编程中,有列表、元组和字典三类变量可以使用,方便数据的存储与处理,而bash中仅有字符串变量、数组、函数可用,方法运用上受到限制,这与bash基于C语言,注重语法结构的严谨有关。而Python等高级语言更…...

git中的cherry-pick和merge有些区别以及cherry-pick怎么用
git中的cherry-pick和merge在使用场景上有些区别: cherry-pick用于将另一个分支的某一次或几次commit应用到当前分支。它可以选择性地拉取代码修改。merge用于将两个分支合并成一个新分支。它会把整个分支上的所有修改都合并过来。 具体区别:cherry-pick通常用于将bug修复从发…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
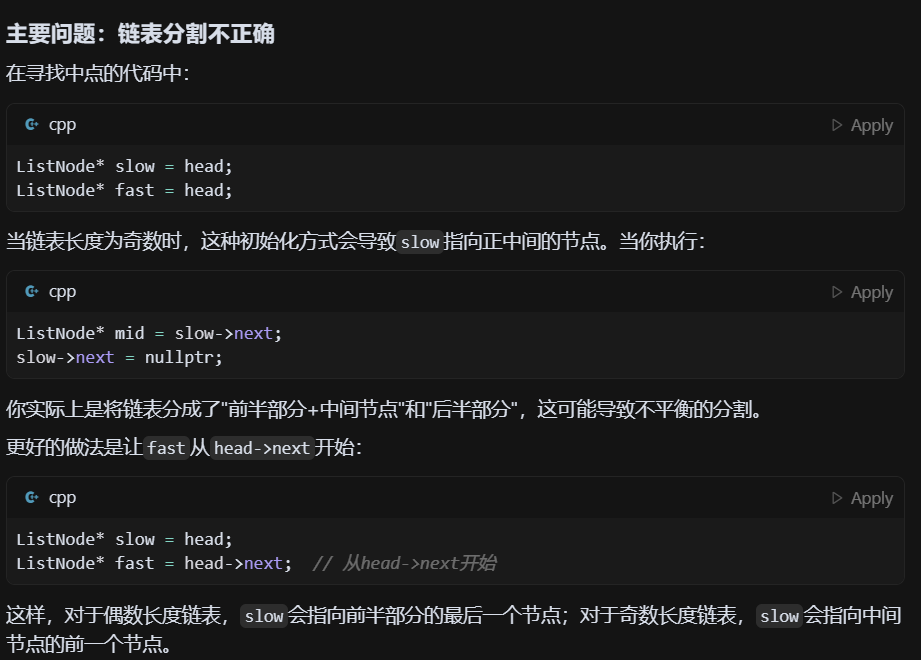
LeetCode - 148. 排序链表
目录 题目 思路 基本情况检查 复杂度分析 执行示例 读者可能出的错误 正确的写法 题目 148. 排序链表 - 力扣(LeetCode) 思路 链表归并排序采用"分治"的策略,主要分为三个步骤: 分割:将链表从中间…...
