二叉树的介绍
写在前面:
二叉树是数据结构课程中非常重要的内容,我们针对二叉树的概念、性质以及类型展开详细介绍。
一、概念
二叉树(Binary Tree)是n(n>=0)个结点的有限集合,该集合或者空集(称为空二叉树),或者由一个根节点和两颗互不相交的,分别称为根节点的左子树和右子树的二叉树组成。其中, 二叉树的最大度为2。
特点:
(1)每个结点最多有两棵子树;
(2)左子树和右子树是有顺序的;
(3)即使树中某结点只有一颗子树,也要区分左右;

图1 二叉树
例如:图1中的E结点,虽然只有一个子树,但是还是要区分左右,图中 I 为右子树。
二、性质
性质1:在二叉树的第i层上至多有2^(i-1)个结点(i≥1)。
性质2:深度为k的二叉树至多有2^(k)-1个结点(k≥1)。
性质3:对任何一颗二叉树T,如果其终端结点数为n_0,度为2的结点数为n_2,则n_0=n_2+1。
性质4:具有n个结点的完全二叉树深度为⌊log2n⌋+1。
其中,满二叉树:深度为k且含有2^(k)-1个结点的二叉树。完全二叉树:深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,称之为完全二叉树。
性质5:如果对有一颗n个结点的完全二叉树(深度为⌊log2n⌋+1)的结点按层序编号(从第1层到第⌊log2n⌋+1层,每层从左到右),则对任一结点i(1≤i≤n),有
(1)如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲PARENT(i)是结点;
(2)如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子LCHILD(i)是结点2i;
(3)如果2i+1>n,则结点i无右孩子(结点i为叶子结点);否则其右孩子RCHILD(i)是结点2i+1。
三、类型
1.满二叉树
除了最后一层的节点没有任何子节点外,每层上的所有节点都有两个节点的二叉树

图2 满二叉树
2.完全二叉树
一颗二叉树的深度为h,除了第h层外,其他各层的节点都有两个子节点,且第h层的所有节点都集中在最左边
(满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树)

图3 完全二叉树
3.二叉搜索树
左子树的所有节点的值均小于它的根节点的值
右子树的所有节点的值均大于它的根节点的值
它的左右子树也分别为二叉搜索树
4.平衡二叉树
平衡二叉树是一颗高度平衡的二叉搜索树;左右两个子树的高度差绝对值不超过1,且左右两个子树都是平衡二叉树;
通过左旋右旋来实现平衡;

图4 平衡二叉树
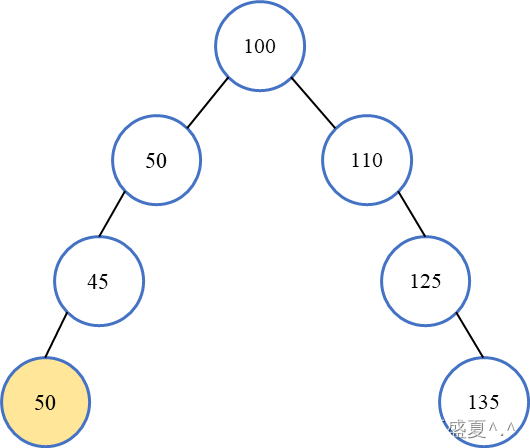
图5 非平衡二叉树
5.红黑树
一种弱平衡的二叉搜索树
(1)每个结点要么是红的,要么是黑的
(2)根节点是黑的
(3)如果一个结点是红色的,那么它的两个子节点都是黑的
(4)每个叶节点都是黑的
(由于是弱平衡,可以看到,在相同的节点的情况下,AVL树的高度低于红黑树),相对于严格要求的AVL树来说,它的旋转次数少,所哟对于搜索,插入和删除操作较多的情况下,可以用红黑树。
6.堆
堆是完全二叉树,所以一定是平衡二叉树。
分为大顶堆和小顶堆
在大顶堆中:父节点的值比每一个子节点的值都要大
在小顶堆中:父节点的值比每一个子节点的值都要小
注意:堆的根节点中存放的是最大或者最小的元素,但是其他节点的排序是未知。例如:在一个大顶堆中,最大的那一个元素总是位于index 0的位置,但是最小的元素则未必是最后一个元素。唯一能保证的是最小的元素是一个叶节点,但是不确定是哪一个。
插入、删除、查找的时间复杂度:
二叉搜索树:最好logn 最坏n 【参考】
平衡二叉搜索树:logn
红黑树:logn
引用
[1]https://blog.csdn.net/AiTTTTTT/article/details/122923963
[2]http://data.biancheng.net/view/192.html
[3]https://blog.csdn.net/peachzy/article/details/116499139
相关文章:

二叉树的介绍
写在前面: 二叉树是数据结构课程中非常重要的内容,我们针对二叉树的概念、性质以及类型展开详细介绍。 一、概念 二叉树(Binary Tree)是n(n>0)个结点的有限集合,该集合或者空集࿰…...
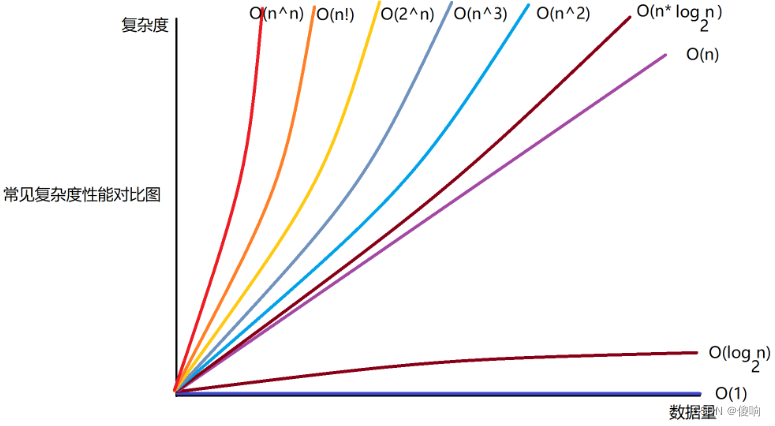
数据结构与算法复杂度介绍
目录 一、基本概念 二、时间复杂度 【2.1】时间复杂度概念 【2.2】大O的渐进表示法 【2.3】举例时间复杂度计算 三、空间复杂度 一、基本概念 数据结构:相互之间存在一种或者多种特定关系的数据元素的集合。在逻辑上可以分为线性结构,散列结构、树…...

CentOS 安装蒲公英
官方教程链接: https://service.oray.com/question/5063.html 教程使用的是2.3版本,官网下载的最新版是2.4,所以命令会有所不同 安装成功后, 任意路径下执行pgyvisitor,调出交互界面pgyvisitor login,登录…...

英语语法基础--思维导图
思维导图通常用于可视化和整理信息,而英文语法非常广泛且复杂,无法在一个简单的思维导图中完整表示。然而,我可以提供一个简化版本的英文语法思维导图,列出一些主要的语法概念和部分示例。 请注意,这只是一个基本的概…...

Android泛型详解
参考文献:https://pingfangx.github.io/java-tutorials/java/generics/types.html 1,什么是泛型? Java泛型(generics)是JDK5中引入的一个新特性,泛型提供了 编译时类型安全检测机制, 该机制允许程序员在编译时检测到…...
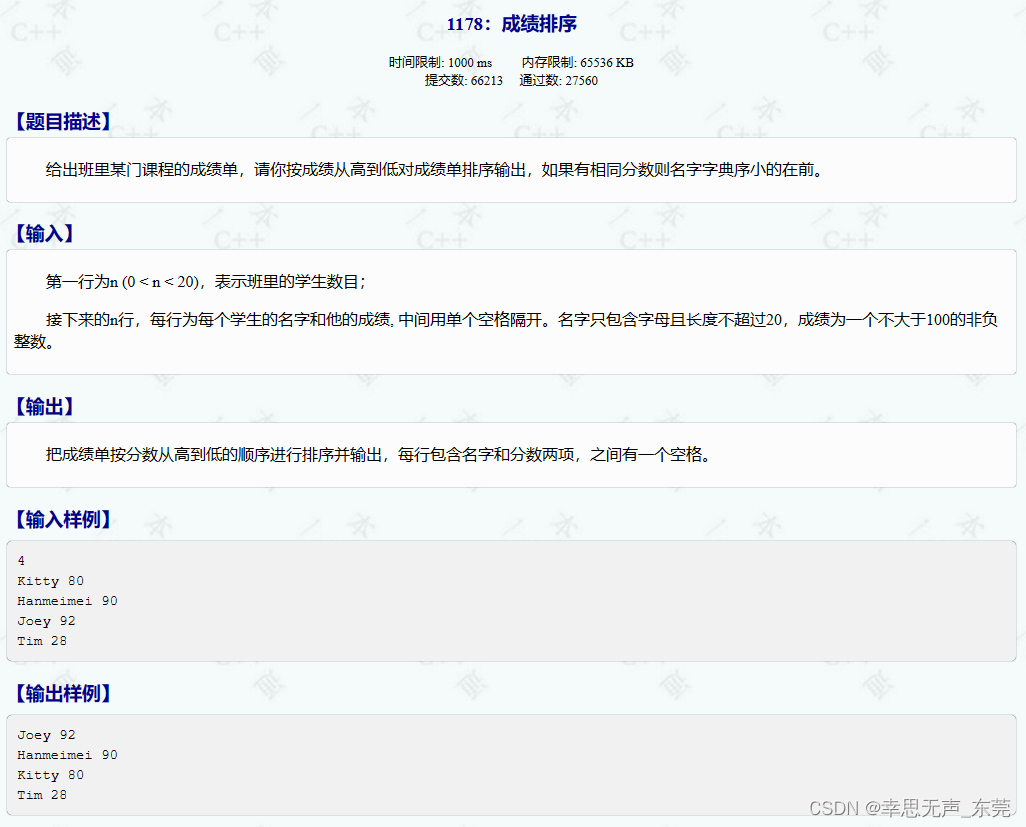
C++信息学奥赛1178:成绩排序
#include<bits/stdc.h> using namespace std; int main(){int n;cin>>n; // 输入整数 n,表示数组的大小int arr[n]; // 创建大小为 n 的整型数组 arrstring brr[n]; // 创建大小为 n 的字符串数组 brrfor(int i0;i<n;i) cin>>brr[i]>>ar…...
)
【计算机视觉 | 目标检测】目标检测常用数据集及其介绍(七)
文章目录 一、Cops-Ref二、FAT (Falling Things)三、GEN1 Detection (Prophesee GEN1 Automotive Detection Dataset)四、RIT-18五、AGAR (Annotated Germs for Automated Recognition)六、EuroCity Persons七、Freiburg Groceries八、Lytro Illum九、PFN-PIC (PFN Picking Ins…...

100天精通Golang(基础入门篇)——第20天:Golang 接口 深度解析☞从基础到高级
🌷🍁 博主猫头虎🐅🐾 带您进入 Golang 语言的新世界✨✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文并茂…...

ESXi 6.7添加螃蟹2.5g网卡支持
安装了ESXi 6.7,结果机器两块网卡只能识别一块,然后想着不能让另一块浪费啊,开始折腾,看着网上都是找的驱动然后封装进iso,可是我已经装完了,怎么办,然后找到了下面解决方法 1.找驱动 下载RTL81…...

机器学习笔记之最优化理论与方法(四) 凸函数:定义与基本性质
机器学习笔记之最优化理论与方法——再回首:凸函数定义与基本性质 引言凸函数的定义严格凸函数凸函数的推论:凹函数 常见凸函数凸函数的基本性质几种保持函数凸性的运算凸集与凸函数之间的关联关系 引言 本节将介绍凸函数定义及其基本性质。 本文是关于…...

【Git】git tag 查看版本号 | 删除本地 | 删除远程仓库| 批量删除
一、删除指定tag 使用场景:比如我们在本地git tag了一个错误的版本号,但是还没有push,想直接删掉避免污染远程仓库 1、删除指令 要删除指定的Git标签(版本号),您可以使用以下命令: git tag -d 标…...
)
thinkphp:数据库查询,嵌套别的表的查询(别的表做子查询)
例子 从 vendors 表中选择记录。在 vendors 表中,筛选出具有满足以下条件的 vendor_code 值: 对应的采购订单(在 po_headers_all 表中)存在未完全接收的采购行(在 po_lines_all 表中)。相应的采购订单状态…...

《Linux 系统命令及Shell脚本实践指南》
Linux 系统命令及Shell脚本实践指南 《Linux 系统命令及Shell脚本实践指南》该书从结构上分为三部分:第一部分1.1Linux的历史发展1.2用户管理1.3任务管理单一时刻执行一次任务使用at周期性任务使用:cron表达式,命令crontab 1.4文件管理1.4.1 Linux shell…...

代码随想录算法训练营第三十八天 | ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
题目链接:509. 斐波那契数 代码随想录 视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili 看完代码随想录之后的想法: 我们要知道动态规划的五部曲; 1,确定dp数组的含义&#x…...
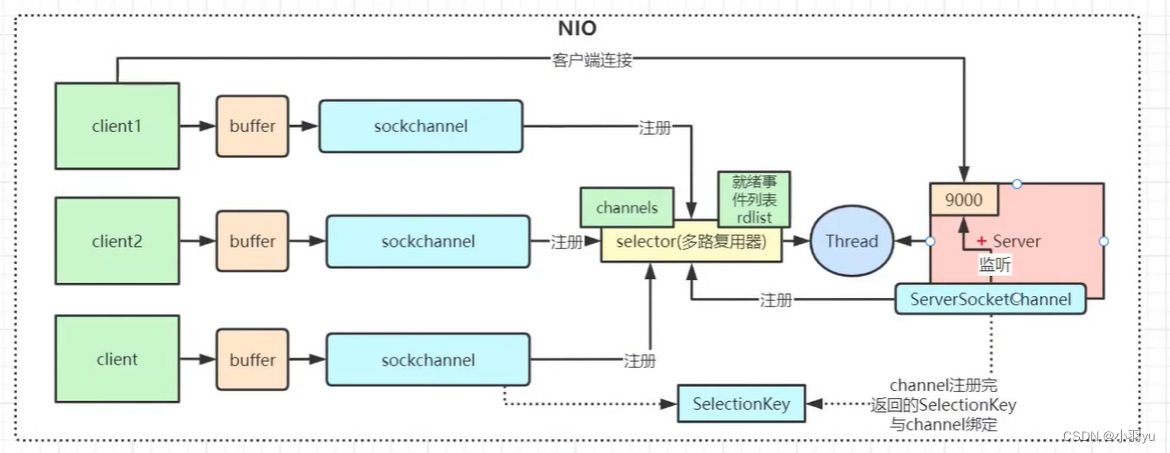
Java分别用BIO、NIO实现简单的客户端服务器通信
分别用BIO、NIO实现客户端服务器通信 BIONIONIO演示(无Selector)NIO演示(Selector) 前言: Java I/O模型发展以及Netty网络模型的设计思想 BIO Java BIO是Java平台上的BIO(Blocking I/O)模型&a…...

React Portals
什么是React Portals React Portals(React 门户)是 React 提供的一种机制,用于将组件渲染到 DOM 树中的不同位置,而不受组件层次结构的限制。它允许你将一个组件的渲染内容“传送”到 DOM 结构中的任何位置,通常用于处…...

Python基础之高级函数
异常捕获 Python中,使用trycatch两个关键字来实现对异常的处理。在我们平时的工作中,异常的出现是在所难免的,但是异常一旦出现,极有可能会直接导致程序崩溃,无法正常运行,所以异常一定要及时的做出对应的…...
CSS3常用的新功能总结
CSS3常用的新功能包括圆角、阴渐变、2D变换、3D旋转、动画、viewpor和媒体查询。 圆角、阴影 border-redius 对一个元素实现圆角效果,是通过border-redius完成的。属性为两种方式: 一个属性值,表示设置所有四个角的半径为相同值ÿ…...
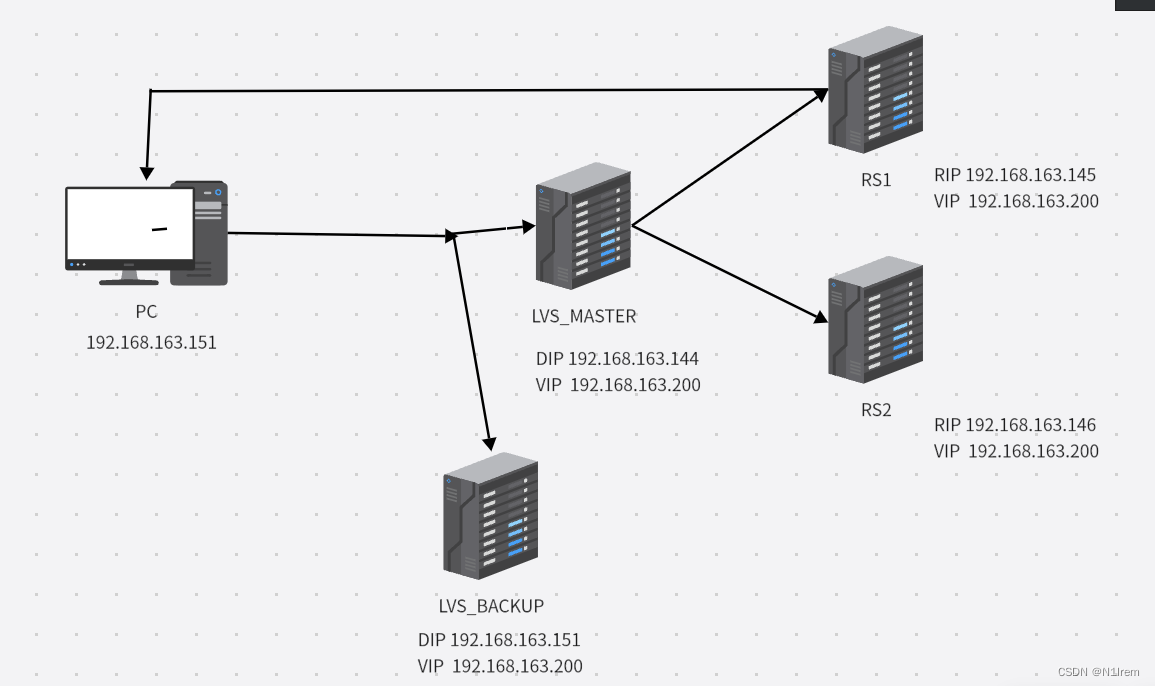
Lvs+KeepAlived高可用高性能负载均衡
目录 1.环境介绍 2.配置keepalived 3.测试 1.测试负载均衡 2.测试RS高可用 3.测试LVS高可用 3.1测试lvs主服务宕机 3.2.测试lvs主服务器恢复 4.我在实验中遇到的错误 1.环境介绍 环境:centos7 RS1---RIP1:192.168.163.145 VIP 192.168.163.200 RS2---RIP2…...

无涯教程-Android Online Test函数
Android在线测试模拟了真正的在线认证考试。您将看到基于 Android概念的多项选择题(MCQ),将为您提供四个options。您将为该问题选择最合适的答案,然后继续进行下一个问题,而不会浪费时间。完成完整的考试后,您将获得在线考试分数。 总问题数-20 最长时间-20分钟 Start Test …...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
