最小生成树Kruskal、Prim算法C++
什么是最小生成树
连通图:
在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1和顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。
生成树:
一个连通图的最小连通子图称作为图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。
最小生成树:
最小生活树是生成树的一个特殊情况,它的边权之和最小。其特点如下:
- 只能使用图中权值最小的边来构造最小生成树
- 只能使用恰好n-1条边来连接图中的n个顶点
- 选用的n-1条边不能构成回路(构成回路会导致有顶点为连通或权值过大)
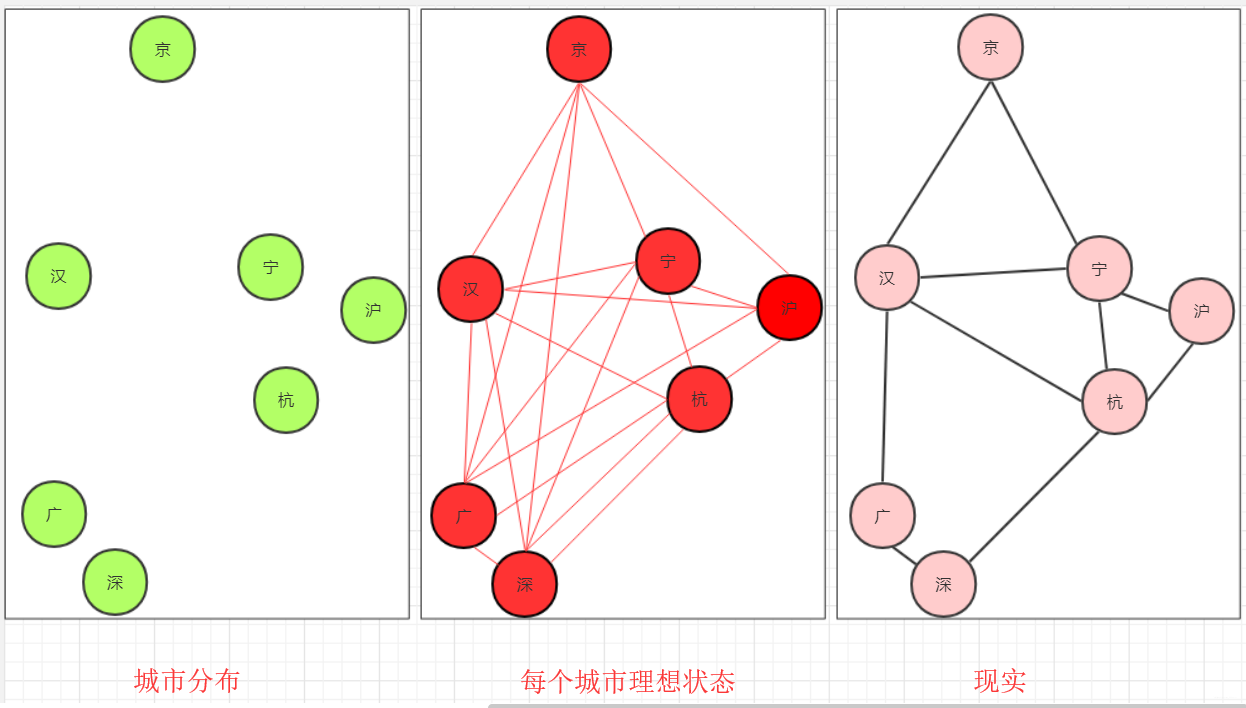
最小生成树的实际应用
例如城市道路铺设中,如果我们直接使用连通结构,这样两点间的交通必然是最便捷的。可是修路的成本的巨大的,但是又要连通所有城市,这便会想到使用最小生成树。
考虑到经济发达城市人口多、车辆多,我们还需要为其多修建一些道路,则实际中的道路修建与最小生成树的结果不同,但是最小生成树在这些实际场景发挥了很大作用。
Kruskal算法
任给一个有n个顶点的连通网络N = {V,E}。
首先构造一个由这n个顶点组成、不含任何边的图G={V,null},其中每个顶点自成一个连通分量,其次不断从E中取出权值最小的一条边(若有多条任取其中之一),若该边的两个顶点来自不同的连通分量,则将此边加入到G中。如此重复,知道所有顶点在同一个连通分量上为止。
算法思路
核心:每次迭代时,选出一条具有最小权值,且两端点不在同一连通分量上的边,加入生成树。
将权值小的边放入到优先级队列中。依次类推
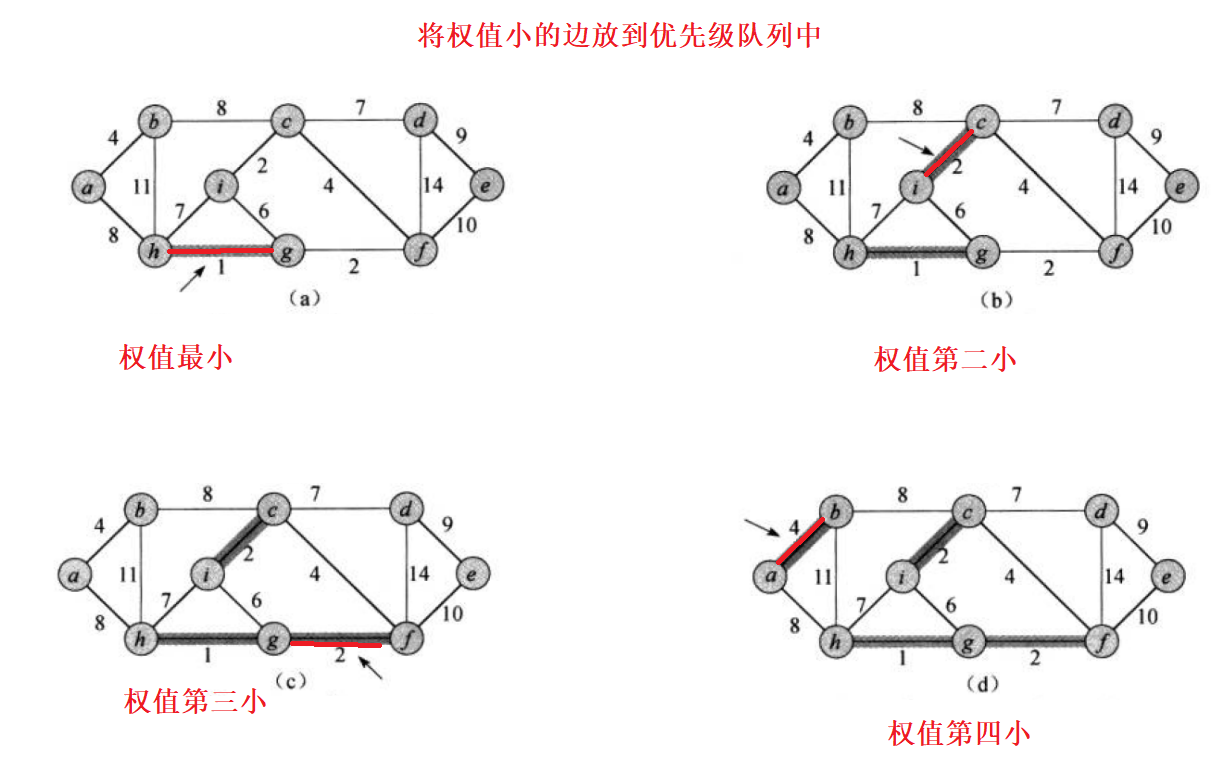
接下来有一个问题,因为生成树不能构成回路,所以在添加边的时候要处理成环问题。
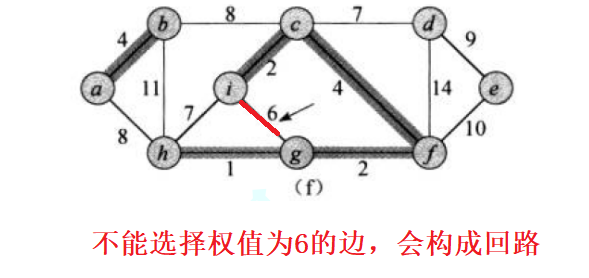
这个问题的解决就要使用并查集;如果该边已经出现过了,则不选择该边,如果该边不在集合中,则可以选择该边
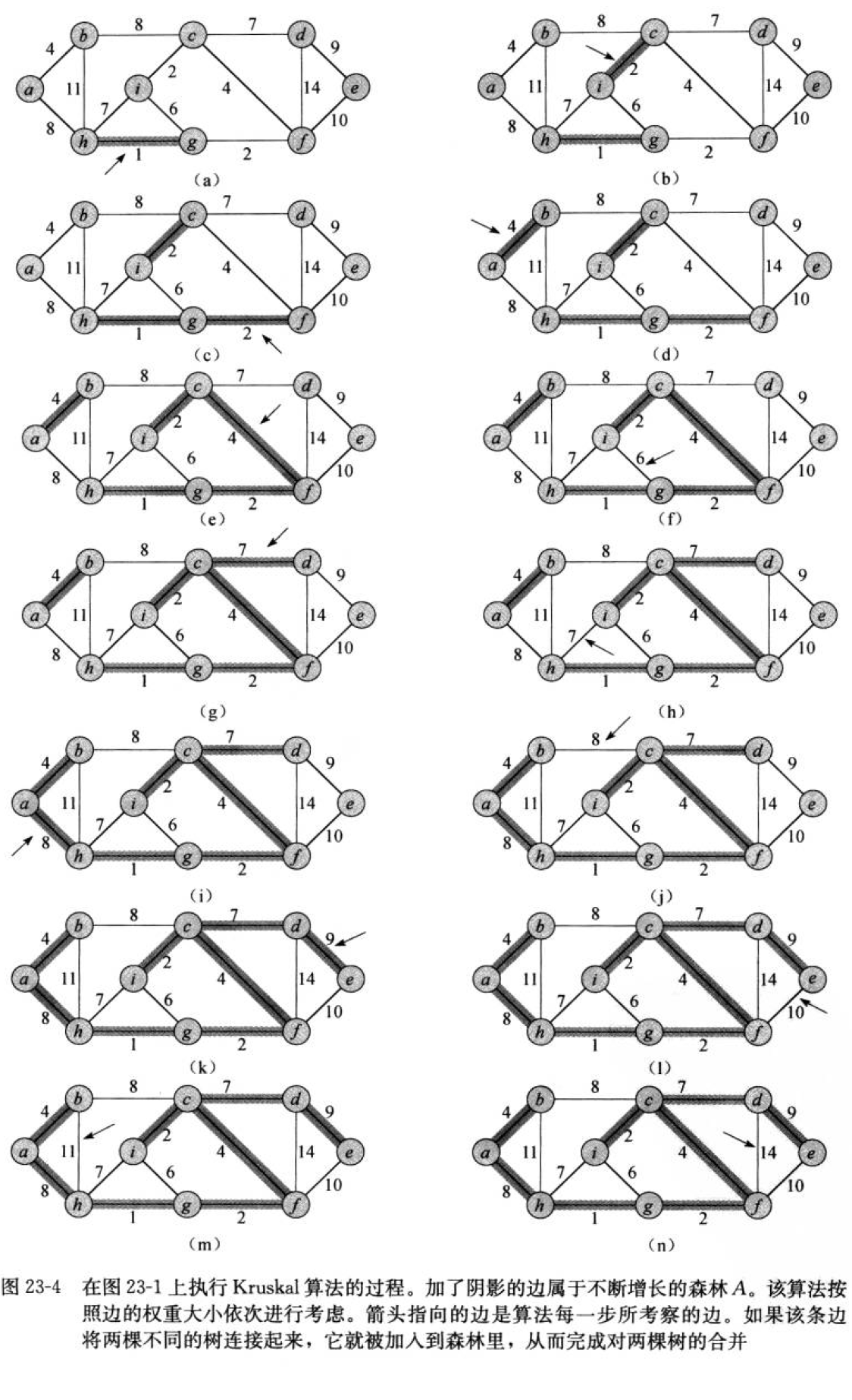
以下是选边的全部过程:
代码实现
首先我们要创建一个边的数据结构Edge,用于将边存放到优先级队列中。
struct Edge
{size_t _srci;size_t _dsti;W _w;Edge(size_t srci, size_t dsti, W w):_srci(srci), _dsti(dsti), _w(w){}//还要提供一个比较函数,因为优先级队列中使用到了greater,greater会调用>函数bool operator > (const Edge& ed) const{return _w > ed._w;}
};实现思路:
1. 将所有的边统计到优先级队列中,(注意临界矩阵只遍历一半)
2. 从优先级队列中选出n-1条边,n为顶点数量
3. 依次取出队列中的元素,判断该元素是否出现过(使用并查集)
4. 如果没有出现过,则添加该边到最小生成树中,并将该边添加到并查集中,再统计权值。
5. 当队列元素取空时,最小生成树中边的数量小于n-1,则表示该图没有连通,则没有最小生成树,直接返回权值的默认值即可。
6. 如果size等于n-1,则表示最小生成树创建成功,返回权值总和即可
//最小生成树
//如果有最小生成树,则返回该树的权值,如果没有最小生成树,则返回默认值
W Kruskal(Self& minTree)
{//初始化minTreesize_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix = vector<vector<W>>(n, vector<W>(n, MAX_W));//1. 将边统计起来,使用优先级队列或排序的方式都可以 priority_queue<Edge, vector<Edge>, greater<Edge>> minque;for (size_t i = 0; i < n; i++){//矩阵中走一半即可 要不然会重复入队列for (size_t j = 0; j < i; j++){if (_matrix[i][j] != MAX_W){minque.push(Edge(i, j, _matrix[i][j]));}}}//2.选出n-1条边size_t size = 0;UnionFindSet ufs(n); //n个顶点W total_W{}; //总的权值while (!minque.empty() && size < n){Edge min = minque.top();minque.pop();//3.选出一条边之后看该边在不在当前集合,//在就不选择该边,不在就选择该边,并标记if (!ufs.IsInset(min._srci, min._dsti)){cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] <<":" << _matrix[min._srci][min._dsti] << endl;minTree._AddEdge(min._srci, min._dsti, min._w);ufs.Union(min._srci, min._dsti);size++;total_W += min._w;}}//如果该图不是连通图,则没有最小生成树if (size < n - 1){return W();}return total_W;
}接下来是一些要注意的点:
1. 要将最小生成树进行初始化,否则添加边时会出现越界问题。
2. 最小生成树其实就是该图的子图,typedef Graph<V, W, MAX_W, Direction> Self;
3. 注意将顶点放入到并查集中,防止边的重复。
测试用例
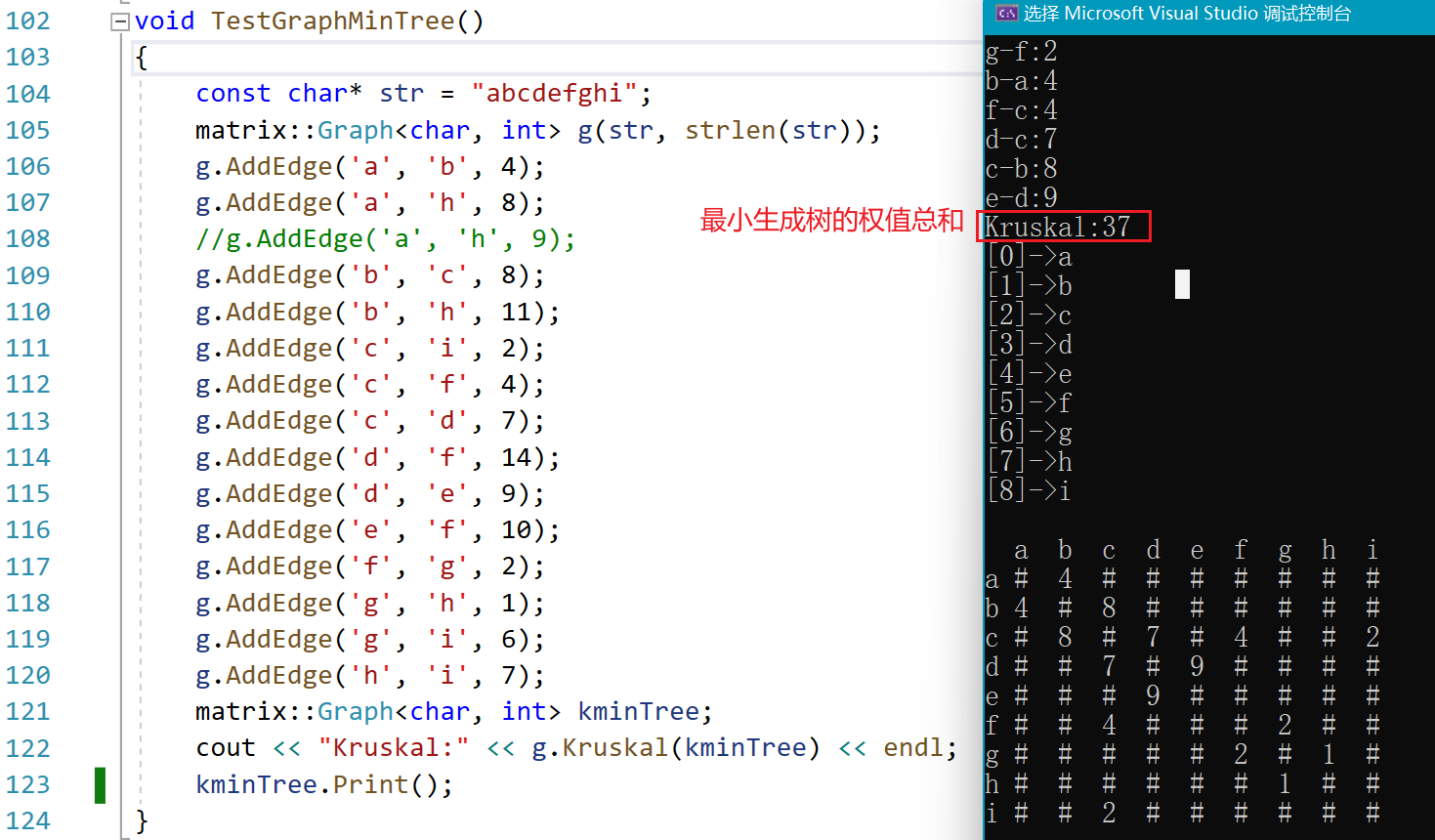
void TestGraphMinTree()
{const char* str = "abcdefghi";matrix::Graph<char, int> g(str, strlen(str));g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);//g.AddEdge('a', 'h', 9);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11);g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);matrix::Graph<char, int> kminTree;cout << "Kruskal:" << g.Kruskal(kminTree) << endl;kminTree.Print();
}
Prim算法
算法思路
Prim算法所具有的一个性质是集合A中的边总是构成一棵树。这棵树从一个任意的根节点r开始,一直扩大到图中的所有顶点为止。在每一步连接集合A和A之外的顶点的所有边中,选择一条权值最小的边加入到A中。当算法结束时,A中的边形成一棵最小生成树。
因为添加边只会在当前集合中没有的顶点中进行,所以Prim算法天然避免环的生成,不需要使用并查集来避免环的产生。
代码实现
实现思路:
1. 使用两个数组表示X、Y集合,用于表示当前顶点是否被访问。
2. 从X集合中的顶点选出所有的边,可以使用优先级队列来存放边。
3. 依次从优先级队列中选出权值最小的边
4. 判断该边是否成环---即dest顶点必须在Y集合中
5. 在Y集合中则将该边添加到最小生成树中,然后进行顶点的标记
6. 再将dest顶点连通的边再放入队列中,同时也要判断dest连接的顶点归属Y集合。
7. 如果选出n-1条边,返回生成树的总权值,否则返回默认值
W Prim(Self& minTree, const W& src) //src表示从哪个起点开始
{size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();//初始化minTreeminTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix = vector<vector<W>>(n, vector<W>(n, MAX_W));//两个数组表示X、Y集合,用于表示当前顶点是否被访问vector<bool> X(n, false);vector<bool> Y(n, true);//初始化X,Y集合X[srci] = true;Y[srci] = false;//从X-Y集合连接中的边选出权值最小的边priority_queue<Edge, vector<Edge>, greater<Edge>> minque;//先把srci连接的边添加到队列中for (size_t i = 0; i < n; i++){if (_matrix[srci][i] != MAX_W){minque.push(Edge(srci, i, _matrix[srci][i]));}}size_t size = 0;W total_W = W();while (!minque.empty()){Edge min = minque.top();minque.pop();if (Y[min._dsti]) //该顶点必须还在Y集合中 注意!!{cout << _vertexs[min._srci] << "-" << _vertexs[min._dsti] <<":" << _matrix[min._srci][min._dsti] << endl;minTree._AddEdge(min._srci, min._dsti, min._w);total_W += min._w;size++;if (size == n - 1)break;X[min._dsti] = true;Y[min._dsti] = false;//将dsti的边进行遍历for (size_t i = 0; i < n; i++){if (_matrix[min._dsti][i] != MAX_W && Y[i]) //有连通,并且是Y集合中的顶点{minque.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}}}}//如果该图不是连通图,则没有最小生成树if (size < n - 1){return W();}return total_W;
}测试用例
void TestGraphMinTree()
{const char str[] = "abcdefghi";matrix::Graph<char, int> g(str, strlen(str));g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11);g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);/*matrix::Graph<char, int> kminTree;cout << "Kruskal:" << g.Kruskal(kminTree) << endl;kminTree.Print();*/cout << "prim算法的实现" << endl;matrix::Graph<char, int> pminTree;cout << "Prim:" << g.Prim(pminTree, 'a') << endl;pminTree.Print();
}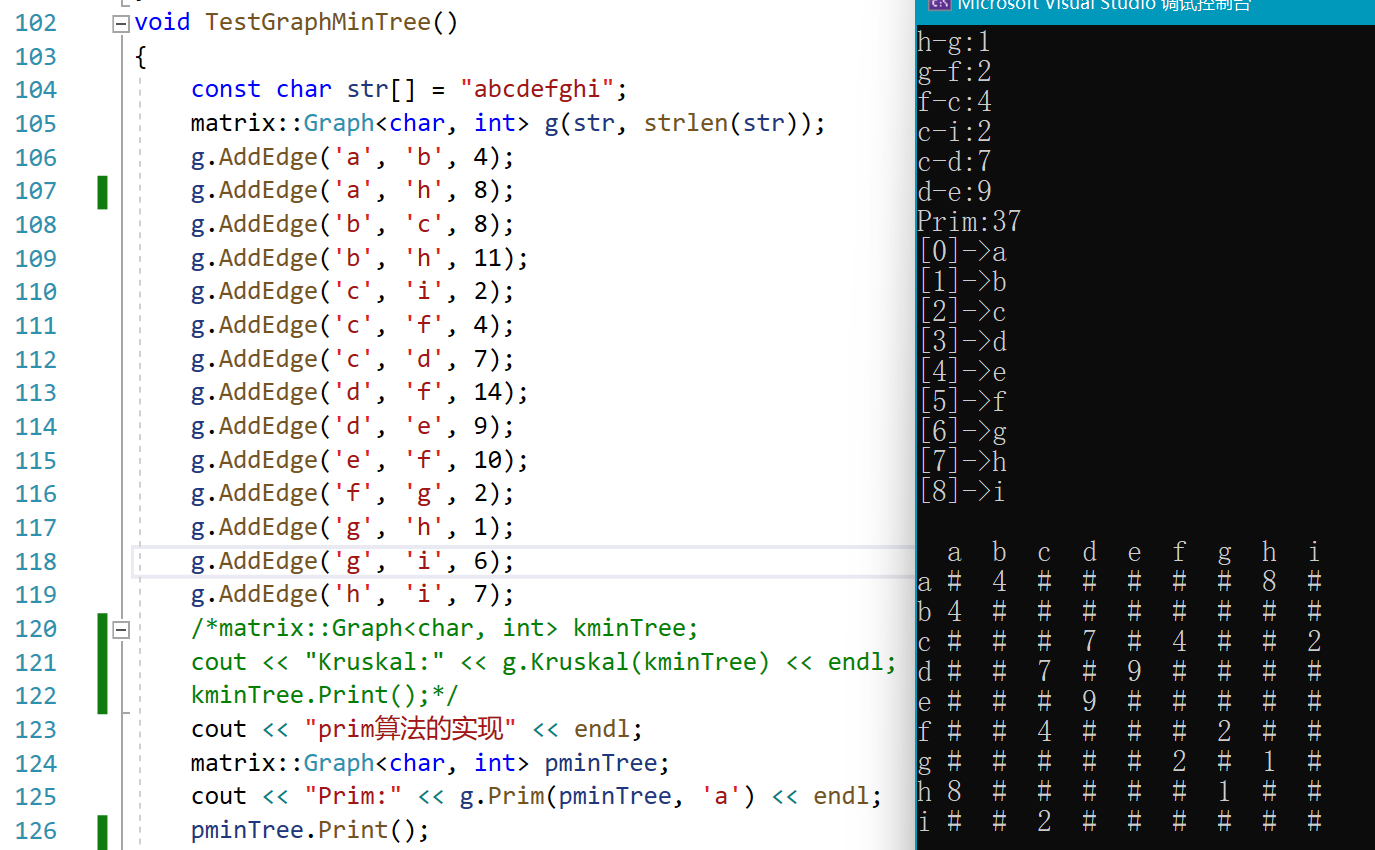
最后细心的你可以会发现,两种算法的结果权值都是37,但是其生成的最小生成树是不同的,这就好比一个正三角形,三个顶点所在的位置,无论连接哪条线,其都是最小生成树,所以不唯一。
相关文章:

最小生成树Kruskal、Prim算法C++
什么是最小生成树 连通图: 在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1和顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。 生成树: 一个连通图的最小连通子图称作为图的生成树。有n个顶点的…...

系统架构设计师-计算机系统基础知识(2)
目录 一、存储管理 1、页式存储 2、段式存储 3、段页式存储 二、磁盘管理 1、先来先服务FCFS 2、最短寻道时间优先SSTF 三、文件系统 1、文件基本概念 2、文件的类型: 3、索引文件结构 4、位示图 四、性能指标 五、性能设计 1、阿姆达尔定律 六、性能评估 1、…...
二叉树的介绍
写在前面: 二叉树是数据结构课程中非常重要的内容,我们针对二叉树的概念、性质以及类型展开详细介绍。 一、概念 二叉树(Binary Tree)是n(n>0)个结点的有限集合,该集合或者空集࿰…...
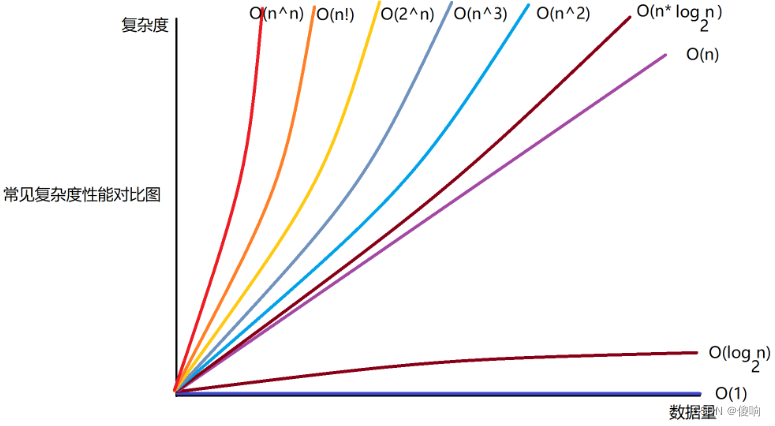
数据结构与算法复杂度介绍
目录 一、基本概念 二、时间复杂度 【2.1】时间复杂度概念 【2.2】大O的渐进表示法 【2.3】举例时间复杂度计算 三、空间复杂度 一、基本概念 数据结构:相互之间存在一种或者多种特定关系的数据元素的集合。在逻辑上可以分为线性结构,散列结构、树…...

CentOS 安装蒲公英
官方教程链接: https://service.oray.com/question/5063.html 教程使用的是2.3版本,官网下载的最新版是2.4,所以命令会有所不同 安装成功后, 任意路径下执行pgyvisitor,调出交互界面pgyvisitor login,登录…...

英语语法基础--思维导图
思维导图通常用于可视化和整理信息,而英文语法非常广泛且复杂,无法在一个简单的思维导图中完整表示。然而,我可以提供一个简化版本的英文语法思维导图,列出一些主要的语法概念和部分示例。 请注意,这只是一个基本的概…...

Android泛型详解
参考文献:https://pingfangx.github.io/java-tutorials/java/generics/types.html 1,什么是泛型? Java泛型(generics)是JDK5中引入的一个新特性,泛型提供了 编译时类型安全检测机制, 该机制允许程序员在编译时检测到…...
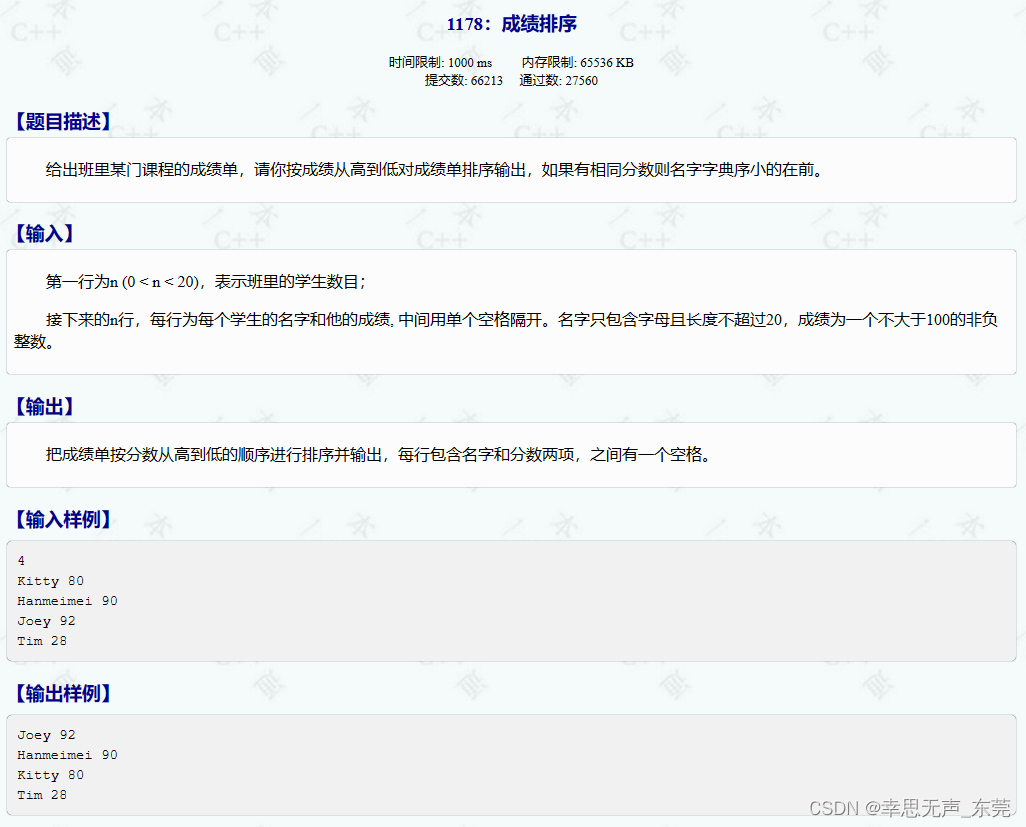
C++信息学奥赛1178:成绩排序
#include<bits/stdc.h> using namespace std; int main(){int n;cin>>n; // 输入整数 n,表示数组的大小int arr[n]; // 创建大小为 n 的整型数组 arrstring brr[n]; // 创建大小为 n 的字符串数组 brrfor(int i0;i<n;i) cin>>brr[i]>>ar…...
)
【计算机视觉 | 目标检测】目标检测常用数据集及其介绍(七)
文章目录 一、Cops-Ref二、FAT (Falling Things)三、GEN1 Detection (Prophesee GEN1 Automotive Detection Dataset)四、RIT-18五、AGAR (Annotated Germs for Automated Recognition)六、EuroCity Persons七、Freiburg Groceries八、Lytro Illum九、PFN-PIC (PFN Picking Ins…...

100天精通Golang(基础入门篇)——第20天:Golang 接口 深度解析☞从基础到高级
🌷🍁 博主猫头虎🐅🐾 带您进入 Golang 语言的新世界✨✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文并茂…...

ESXi 6.7添加螃蟹2.5g网卡支持
安装了ESXi 6.7,结果机器两块网卡只能识别一块,然后想着不能让另一块浪费啊,开始折腾,看着网上都是找的驱动然后封装进iso,可是我已经装完了,怎么办,然后找到了下面解决方法 1.找驱动 下载RTL81…...

机器学习笔记之最优化理论与方法(四) 凸函数:定义与基本性质
机器学习笔记之最优化理论与方法——再回首:凸函数定义与基本性质 引言凸函数的定义严格凸函数凸函数的推论:凹函数 常见凸函数凸函数的基本性质几种保持函数凸性的运算凸集与凸函数之间的关联关系 引言 本节将介绍凸函数定义及其基本性质。 本文是关于…...

【Git】git tag 查看版本号 | 删除本地 | 删除远程仓库| 批量删除
一、删除指定tag 使用场景:比如我们在本地git tag了一个错误的版本号,但是还没有push,想直接删掉避免污染远程仓库 1、删除指令 要删除指定的Git标签(版本号),您可以使用以下命令: git tag -d 标…...
)
thinkphp:数据库查询,嵌套别的表的查询(别的表做子查询)
例子 从 vendors 表中选择记录。在 vendors 表中,筛选出具有满足以下条件的 vendor_code 值: 对应的采购订单(在 po_headers_all 表中)存在未完全接收的采购行(在 po_lines_all 表中)。相应的采购订单状态…...

《Linux 系统命令及Shell脚本实践指南》
Linux 系统命令及Shell脚本实践指南 《Linux 系统命令及Shell脚本实践指南》该书从结构上分为三部分:第一部分1.1Linux的历史发展1.2用户管理1.3任务管理单一时刻执行一次任务使用at周期性任务使用:cron表达式,命令crontab 1.4文件管理1.4.1 Linux shell…...

代码随想录算法训练营第三十八天 | ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
题目链接:509. 斐波那契数 代码随想录 视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili 看完代码随想录之后的想法: 我们要知道动态规划的五部曲; 1,确定dp数组的含义&#x…...
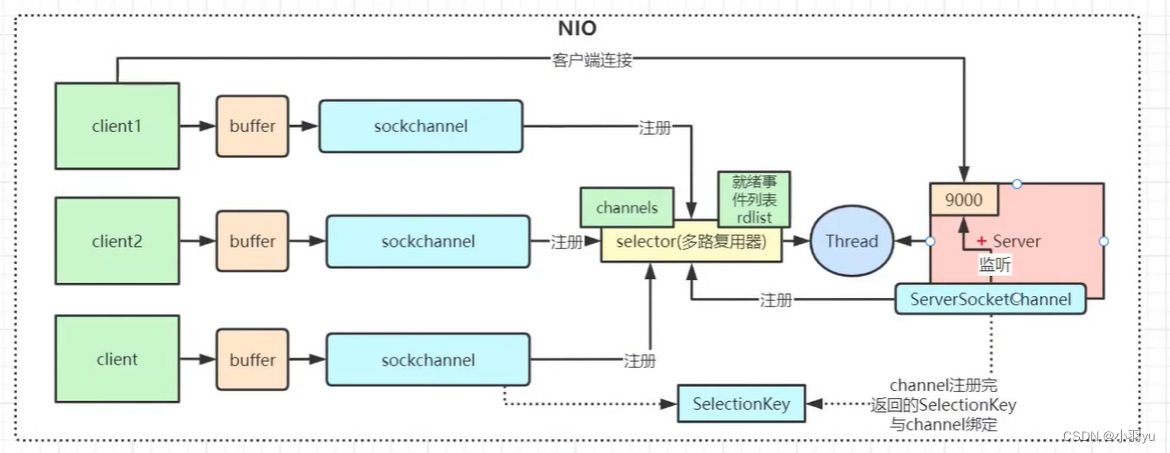
Java分别用BIO、NIO实现简单的客户端服务器通信
分别用BIO、NIO实现客户端服务器通信 BIONIONIO演示(无Selector)NIO演示(Selector) 前言: Java I/O模型发展以及Netty网络模型的设计思想 BIO Java BIO是Java平台上的BIO(Blocking I/O)模型&a…...

React Portals
什么是React Portals React Portals(React 门户)是 React 提供的一种机制,用于将组件渲染到 DOM 树中的不同位置,而不受组件层次结构的限制。它允许你将一个组件的渲染内容“传送”到 DOM 结构中的任何位置,通常用于处…...

Python基础之高级函数
异常捕获 Python中,使用trycatch两个关键字来实现对异常的处理。在我们平时的工作中,异常的出现是在所难免的,但是异常一旦出现,极有可能会直接导致程序崩溃,无法正常运行,所以异常一定要及时的做出对应的…...
CSS3常用的新功能总结
CSS3常用的新功能包括圆角、阴渐变、2D变换、3D旋转、动画、viewpor和媒体查询。 圆角、阴影 border-redius 对一个元素实现圆角效果,是通过border-redius完成的。属性为两种方式: 一个属性值,表示设置所有四个角的半径为相同值ÿ…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
